Всё о треугольниках

1. Проект на тему: «Всё о треугольниках»

Выполнила:
Ученица 11 класса МБОУ
«СОШ №1 Саратовской области Самойловского района»
Еремина Карина.
Руководитель: Очеретова Тамара Ивановна.

2.

Цели:
Систематизировать понятия по теме «Все о треугольниках»;
Показать практическое применение данного материала при решении
задач при подготовке к ЕГЭ;
Научиться сравнивать треугольники между собой;
Выяснить, каковы особенности каждого треугольника.
Проблема:
Выяснить, насколько важна данная тема при подготовке к ЕГЭ.

3. Содержание

Виды треугольников;
Биссектрисы;
Свойства треугольников;
Средняя линия;
Прямоугольный
треугольник;
Серединный
перпендикуляр;
Равнобедренный
треугольник;
Площадь треугольника;
Теоремы косинусов и
синусов;
Подобие треугольников;
Окружность, вписанная в
треугольник;
Окружность, описанная
около треугольника.
Правильный
треугольник;
Равенство
треугольников;
Медианы;
Высоты;

4. Виды треугольников

В ИДЫ
ТРЕУГОЛЬНИКОВ
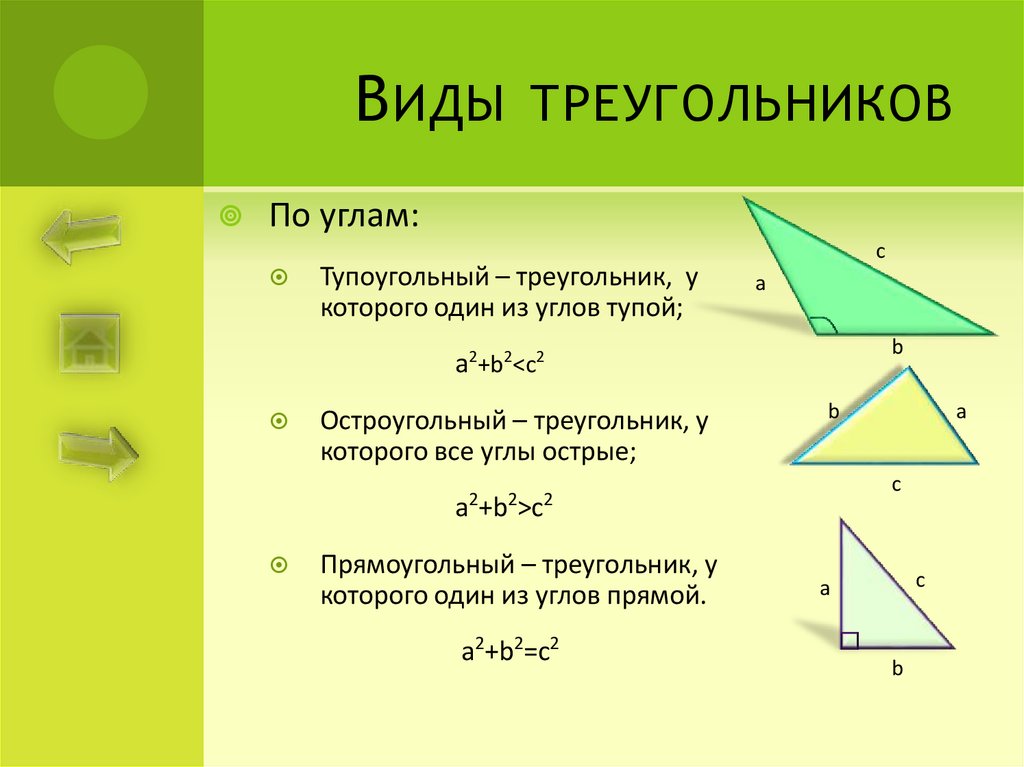
По углам:
с
Тупоугольный – треугольник, у
которого один из углов тупой;
а
b
а2+b2<c2
Остроугольный – треугольник, у
которого все углы острые;
2
2
а +b >c
b
с
2
Прямоугольный – треугольник, у
которого один из углов прямой.
а2+b2=c2
а
с
а
b

5. Виды треугольников

В ИДЫ
ТРЕУГОЛЬНИКОВ
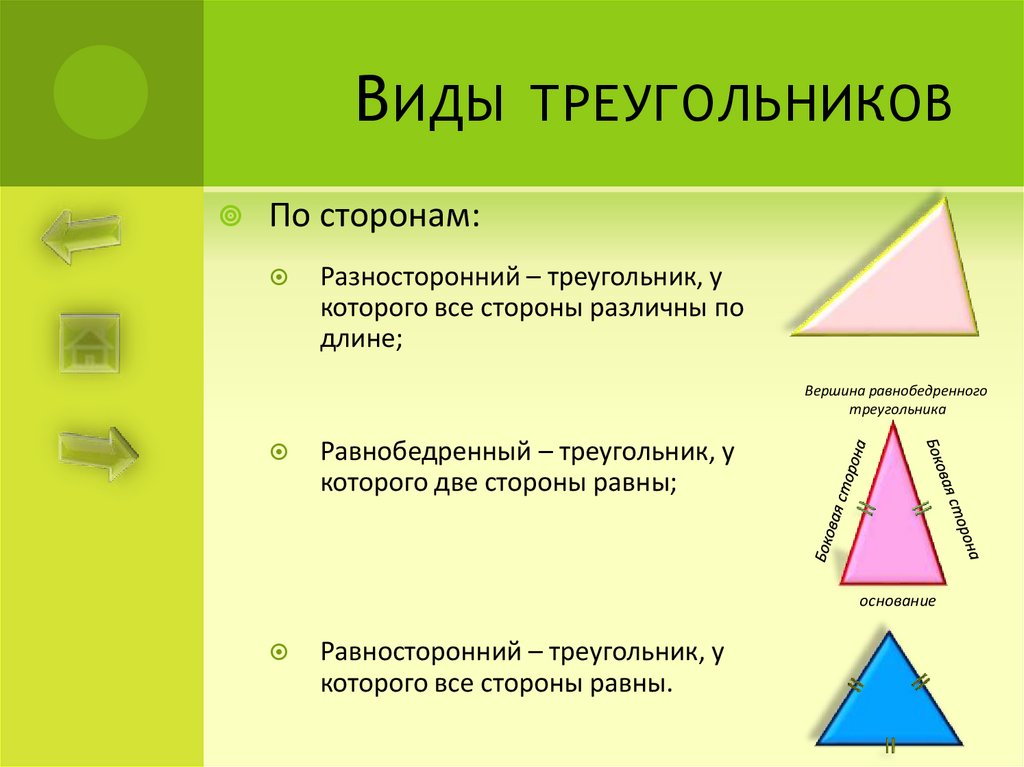
По сторонам:
Разносторонний – треугольник, у
которого все стороны различны по
длине;
Вершина равнобедренного
треугольника
Равнобедренный – треугольник, у
которого две стороны равны;
основание
Равносторонний – треугольник, у
которого все стороны равны.

6. Свойства треугольников

С ВОЙСТВА
ТРЕУГОЛЬНИКОВ
Сумма углов треугольника равна 1800
0
1+ 2+ 3=180 ;
Внешний угол треугольника равен сумме
двух внутренних, не смежных с ним, углов
4= 2+ 3;
2
b
В любом треугольнике каждая сторона
меньше суммы двух других сторон
4
а
1
3
с
а<b+с, b<а+с, с<а+b;
В треугольнике против большей стороны
лежит больший угол, против большего угла –
большая сторона.

7. Прямоугольный треугольник

П РЯМОУГОЛЬНЫЙ
ТРЕУГОЛЬНИК
Сторона прямоугольного треугольника,
противолежащая прямому углу, называется
гипотенузой, две другие стороны называются
катетами.
Теорема Пифагора:
Квадрат длины гипотенузы равен сумме квадратов
длин катетов.
а2+b2=c2
1
S ab;
2
1
S ch,
2
с
а
гипотенуза
катет
h – высота, проведенная к гипотенузе
h
b
катет

8. Свойства прямоугольного треугольника

С ВОЙСТВА ПРЯМОУГОЛЬНОГО
ТРЕУГОЛЬНИКА
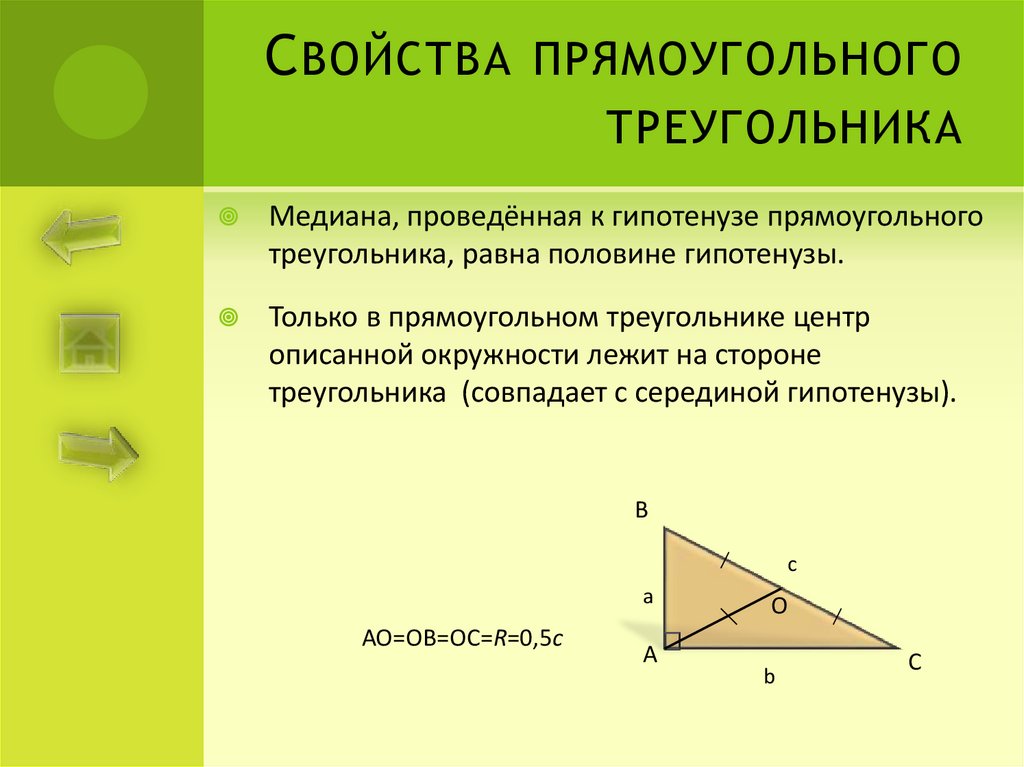
Медиана, проведённая к гипотенузе прямоугольного
треугольника, равна половине гипотенузы.
Только в прямоугольном треугольнике центр
описанной окружности лежит на стороне
треугольника (совпадает с серединой гипотенузы).
В
с
а
АО=ОВ=ОС=R=0,5с
А
О
b
С

9. Признаки прямоугольных треугольников

П РИЗНАКИ ПРЯМОУГОЛЬНЫХ
ТРЕУГОЛЬНИКОВ
Если квадрат одной из сторон треугольника равен
сумме квадратов двух других сторон, то такой
треугольник прямоугольный.
Если медиана треугольника равна половине
соответствующей ей стороны, то треугольник
прямоугольный.

10. Свойства равнобедренного треугольника

С ВОЙСТВА РАВНОБЕДРЕННОГО
ТРЕУГОЛЬНИКА
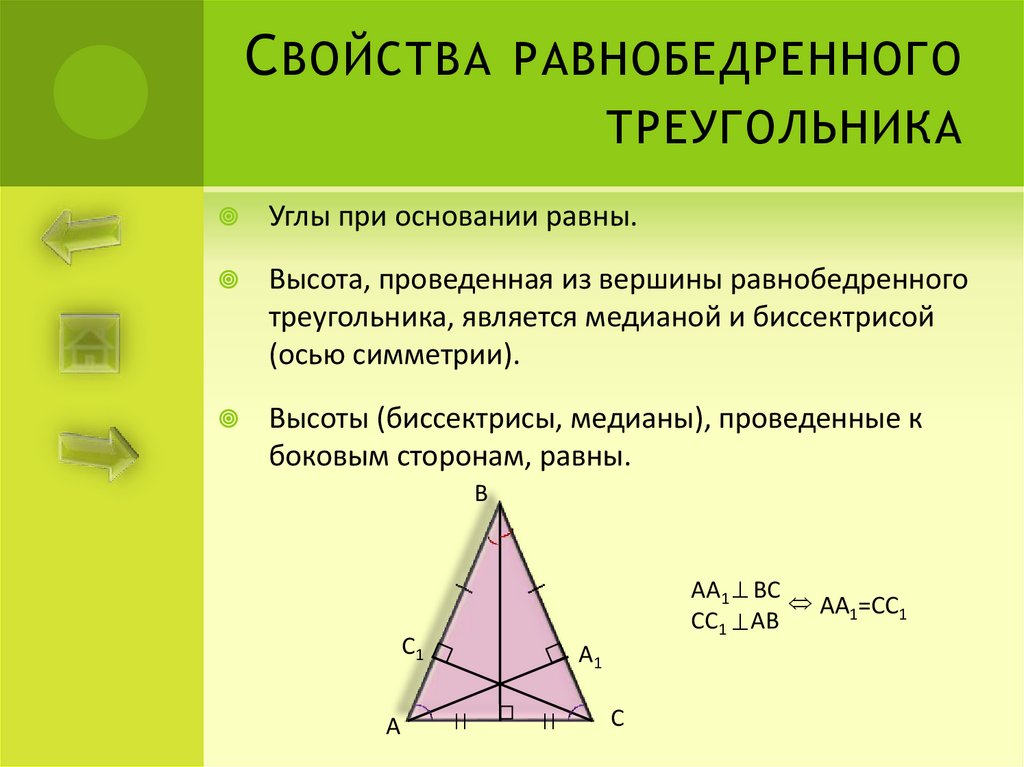
Углы при основании равны.
Высота, проведенная из вершины равнобедренного
треугольника, является медианой и биссектрисой
(осью симметрии).
Высоты (биссектрисы, медианы), проведенные к
боковым сторонам, равны.
В
С1
А
АА1 ВС
АА1=СС1
СС1 АВ
А1
С

11. Свойства правильного треугольника

С ВОЙСТВА ПРАВИЛЬНОГО
ТРЕУГОЛЬНИКА
Все углы равностороннего треугольника равны 60◦.
Только в правильном треугольнике совпадают точки
пересечения медиан, биссектрис, высот, серединных
перпендикуляров. Эта точка называется центром правильного
треугольника и является центром вписанной и описанной
окружностей.
Центр правильного треугольника делит его высоты в
отношении 2:1, считая от вершины.
Только в правильном треугольнике R 2r h
2
3
В
АВ=ВС=АС=а
АА1=ВВ1=СС1=h
h
3
a
2
S
а
С1
2
4
3
О
А
А1
С
В1
a
3

12. Признаки равенства треугольников

П РИЗНАКИ
РАВЕНСТВА ТРЕУГОЛЬНИКОВ
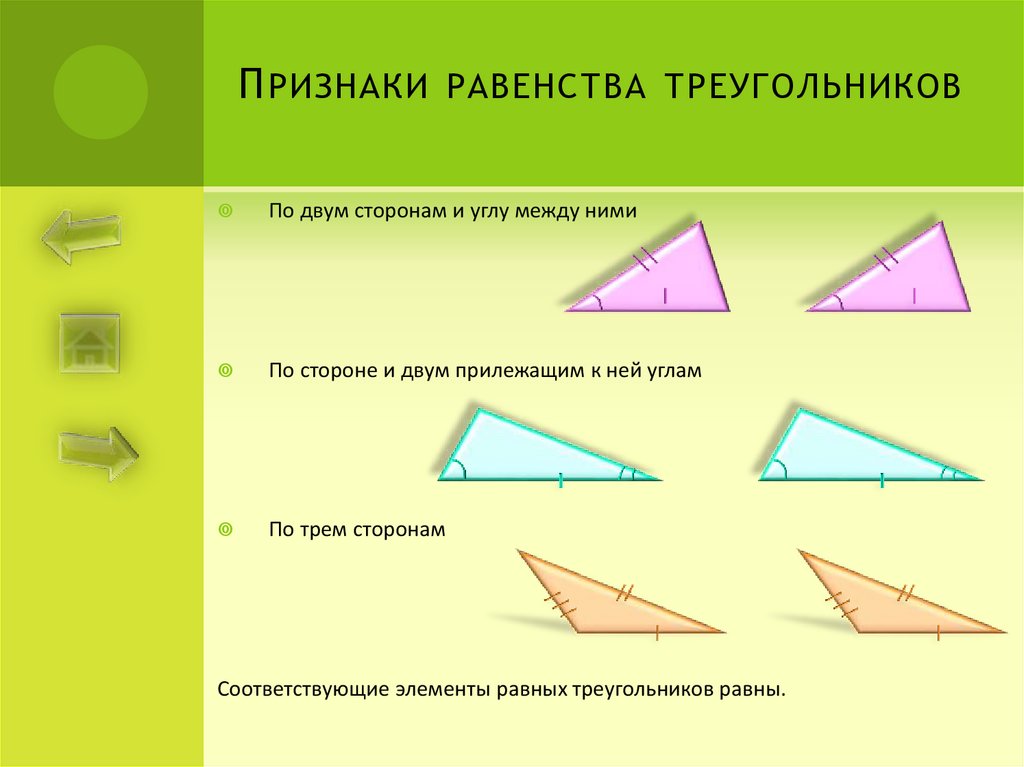
По двум сторонам и углу между ними
По стороне и двум прилежащим к ней углам
По трем сторонам
Соответствующие элементы равных треугольников равны.

13. Медианы

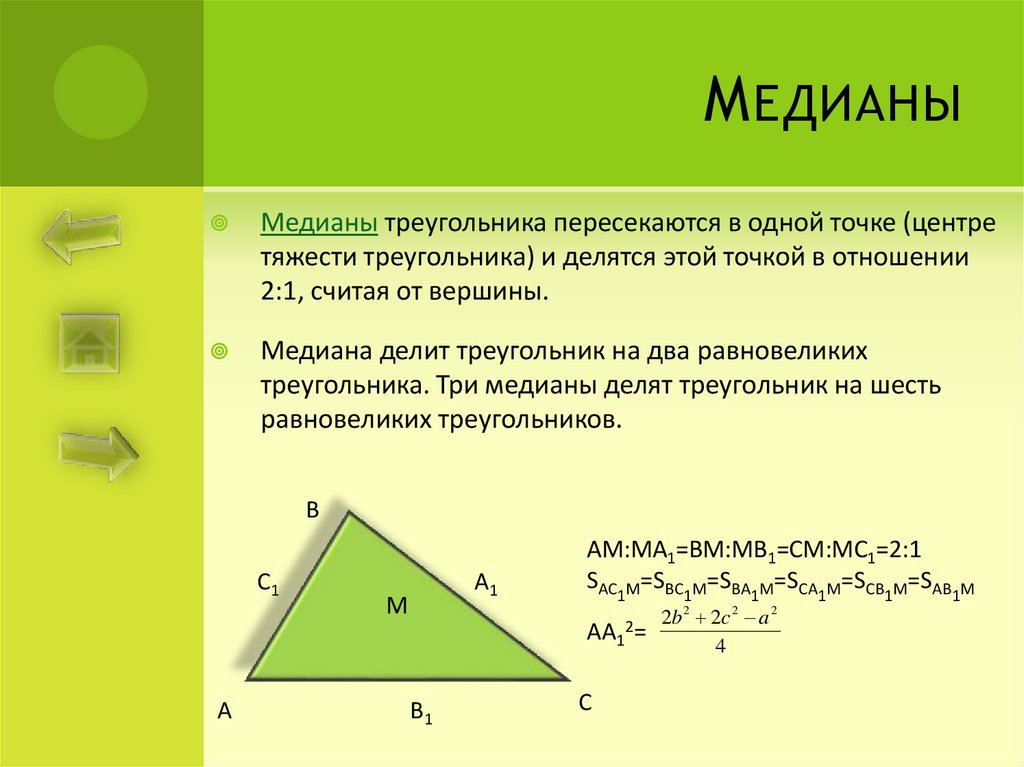
М ЕДИАНЫ
Медианы треугольника пересекаются в одной точке (центре
тяжести треугольника) и делятся этой точкой в отношении
2:1, считая от вершины.
Медиана делит треугольник на два равновеликих
треугольника. Три медианы делят треугольник на шесть
равновеликих треугольников.
В
С1
А1
М
АМ:МА1=ВМ:МВ1=СМ:МС1=2:1
SАС1М=SВС1М=SВА1М=SCА1М=SСВ1М=SАВ1М
АА1
А
В1
С
2=
2b 2 2c 2 a 2
4

14. Биссектрисы

Б ИССЕКТРИСЫ
Все биссектрисы треугольника пересекаются в одной
точке – центре вписанной в треугольник окружности.
Биссектриса делит противолежащую сторону на
отрезки, пропорциональные прилежащим сторонам
треугольника.
В
С1
СА1 СА
;
А1 В АВ
А
А1
О
В1
С

15. Средняя линия

С РЕДНЯЯ
ЛИНИЯ
Средняя линия параллельна третьей стороне и
равна ее половине.
В
Р
А
О
С
РОllАС,
РО=0,5 АС

16. Серединный перпендикуляр

С ЕРЕДИННЫЙ
ПЕРПЕНДИКУЛЯР
Все серединные перпендикуляры сторон
треугольника пересекаются в одной точке – центре
описанной около треугольника окружности. Около
каждого треугольника можно описать окружность и
при том только одну.
Точка пересечения серединных перпендикуляров
треугольника является точкой пересечения высот
треугольника, образованного средними линиями
данного треугольника.

17. Площадь треугольника

П ЛОЩАДЬ
ТРЕУГОЛЬНИКА
o
S∆ = 0,5 aha= 0,5 bhb= 0,5 chc
o
S∆ = 0,5 ab sin C = 0,5 ac sin B = 0,5 bc sin A
o
S∆ =
o
S∆ = rp
o
S∆ =
p(p-a)(p-b)(p-c) (формула Герона)
В
abc
4R
с
А
а
b
p=0,5(a+b+c)
r – радиус вписанной окружности
R – радиус описанной окружности
С

18. Теоремы синусов и косинусов

Т ЕОРЕМЫ СИНУСОВ И
КОСИНУСОВ
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов
двух других сторон без удвоенного произведения этих
сторон на косинус угла между ними.
a2 = b2+c2-2bc cos A
Теорема синусов
Стороны треугольника пропорциональны синусам
противолежащих им углов.
a
b
c
2R
sin A sin B sin C

19. Подобные треугольники

П ОДОБНЫЕ ТРЕУГОЛЬНИКИ
Определение.
Два треугольника называются подобными, если их
углы соответственно равны и стороны одного
треугольника пропорциональны сходственным
сторонам другого.
Обозначение: ∆АВС ~ ∆А1В1С1
В1
В
А
С
А1
С1

20. Признаки подобия треугольников

П РИЗНАКИ
ПОДОБИЯ ТРЕУГОЛЬНИКОВ
По двум углам
По двум сторонам и углу между ними
а
b
kа
kb
По трем сторонам
b
а
с
kа
kb
kс

21. Окружность, вписанная в треугольник

О КРУЖНОСТЬ ,
ВПИСАННАЯ В ТРЕУГОЛЬНИК
В каждый треугольник можно вписать окружность и
при том только одну.
Её центр – точка пересечения биссектрис.
Радиус (r) вычисляется по формулам:
r p a tg
p a p b p c S
r
r
A
B
C
p b tg p c tg
2
2
2
p
p
S
p
ОР АВ; ОК ВС; ОМ АС
АР = АМ = р-а; ВР = ВК = р-b
К КС = МС = р-с
В
Р
О
p - полупериметр
А
М
С

22. Окружность, описанная около треугольника

О КРУЖНОСТЬ ,
ОПИСАННАЯ ОКОЛО ТРЕУГОЛЬНИКА
Около каждого треугольника можно описать
окружность и при том только одну.
Её центр – точка пересечения серединных
перпендикуляров к сторонам треугольника.
Радиус (R) вычисляется по формулам:
a
b
c
2 sin A 2 sin B 2 sin C
abc
R
4S
R
В
С1
АВ1=В1С; АС1=С1В; ВА1=А1С
ОА ВС; ОВ АС;
А
ОА=ОВ=ОС=R
О
В1
А1
С

23.

Внешним углом треугольника называется угол,
смежный с каким-нибудь углом этого
треугольника.
4
4 – внешний угол

24.

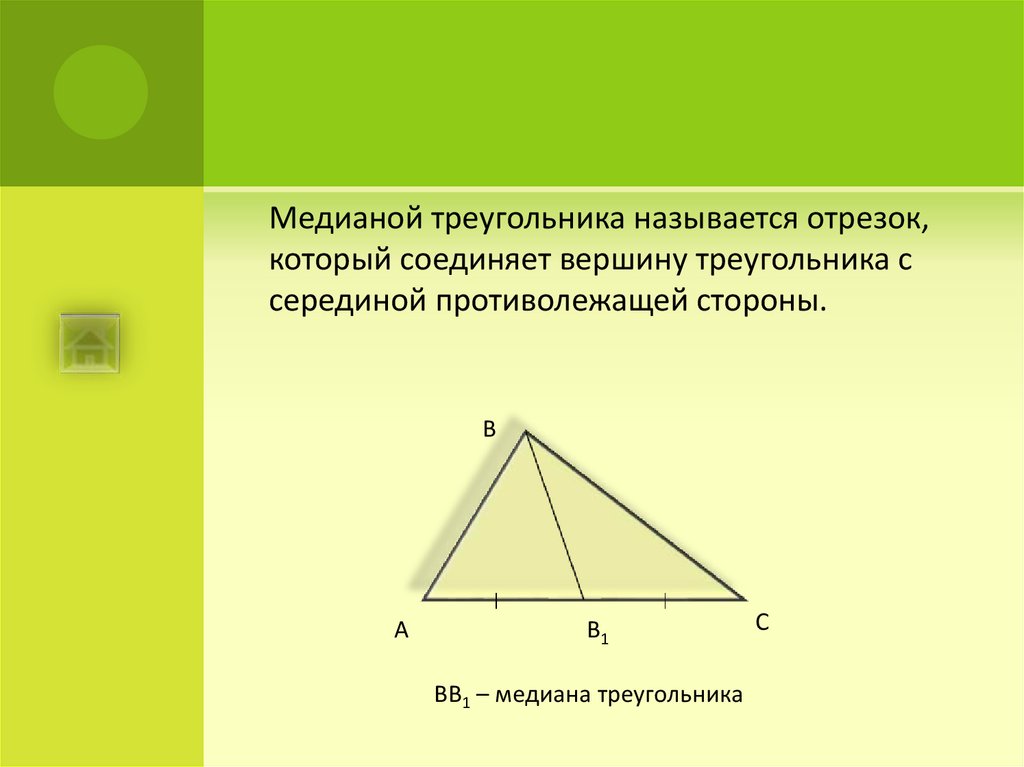
Медианой треугольника называется отрезок,
который соединяет вершину треугольника с
серединой противолежащей стороны.
В
А
В1
ВВ1 – медиана треугольника
С

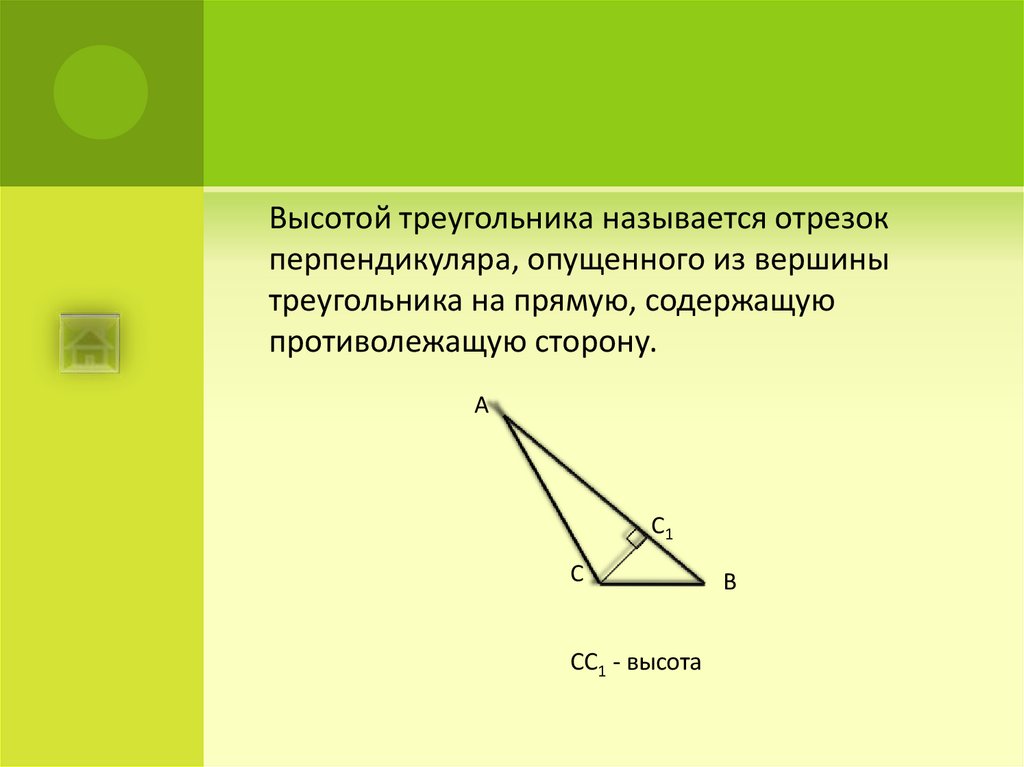
25.

Высотой треугольника называется отрезок
перпендикуляра, опущенного из вершины
треугольника на прямую, содержащую
противолежащую сторону.
А
С1
С
СС1 - высота
В

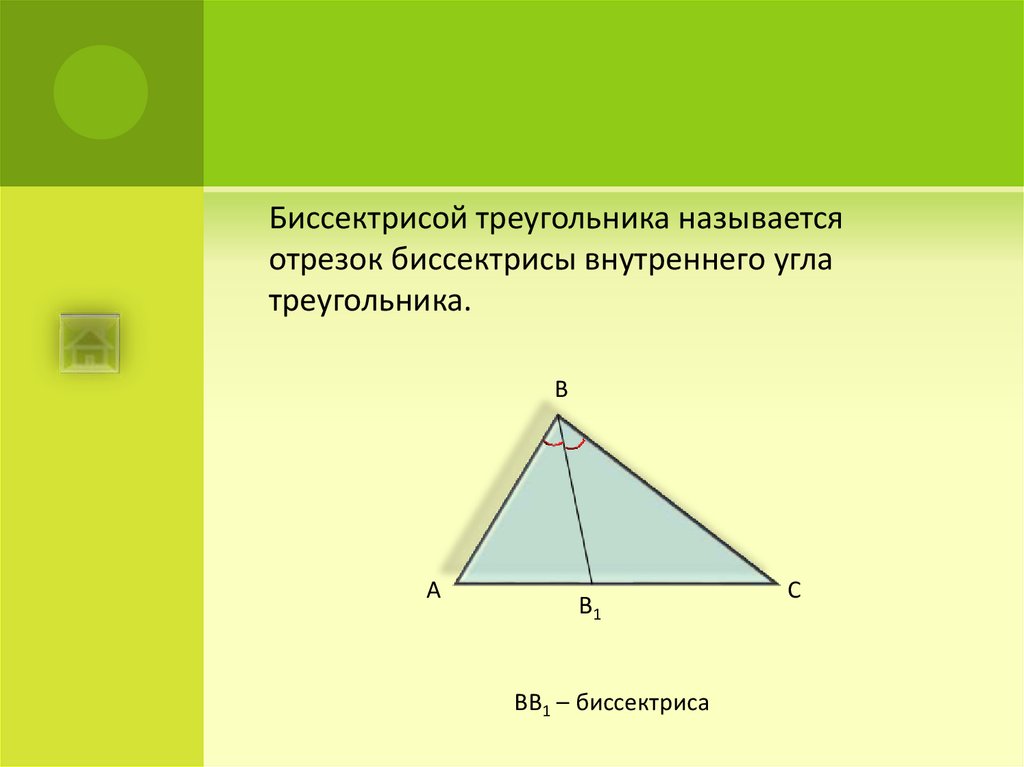
26.

Биссектрисой треугольника называется
отрезок биссектрисы внутреннего угла
треугольника.
В
А
В1
ВВ1 – биссектриса
С

27.

Средней линией треугольника называется
отрезок, соединяющий середины двух сторон
треугольника.
В
Р
А
О
С
РО – средняя линия

28.

Серединным перпендикуляром называется
прямая, перпендикулярная стороне треугольника
и делящая её пополам.
В
А
В1
С

29.

Если в треугольниках углы равны, то стороны,
лежащие против соответственно равных
углов в этих треугольниках, называются
сходственными.
В1
В
А
С
А1
АВ и А1В1, ВС и В1С1, СА и С1А1 – сходственные
стороны
С1

30. Заключение

Осуществление этого проекта позволило
мне углубить мои знания о
треугольниках и математике в целом, а
также выяснить, что данная тема
очень важна для сдачи ЕГЭ.

31. Литература

Л ИТЕРАТУРА
Геометрия, 7-9: учеб. для общеобразоват.
учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б.
Кадомцев и др. – 15-е изд.- М. : Просвещение,
2005.
Геометрия в таблицах. 7-11 кл. : Справочное
пособие/ Авт.-сост. Л.И. Звавич,
А.Р.Рязановский. – 5-е изд., стереотип.- М.:
Дрофа, 2001.