Похожие презентации:
Некоторые следствия из аксиом
1. Некоторые следствия из аксиом
2. Теорема (о плоскости, проходящей через прямую и не лежащую на ней точку). Через прямую и не лежащую на ней точку проходит
плоскость, и притом только однаДано: a, А a
Доказать:
Ι)проходит плоскость
;
ΙΙ) плоскость единственная
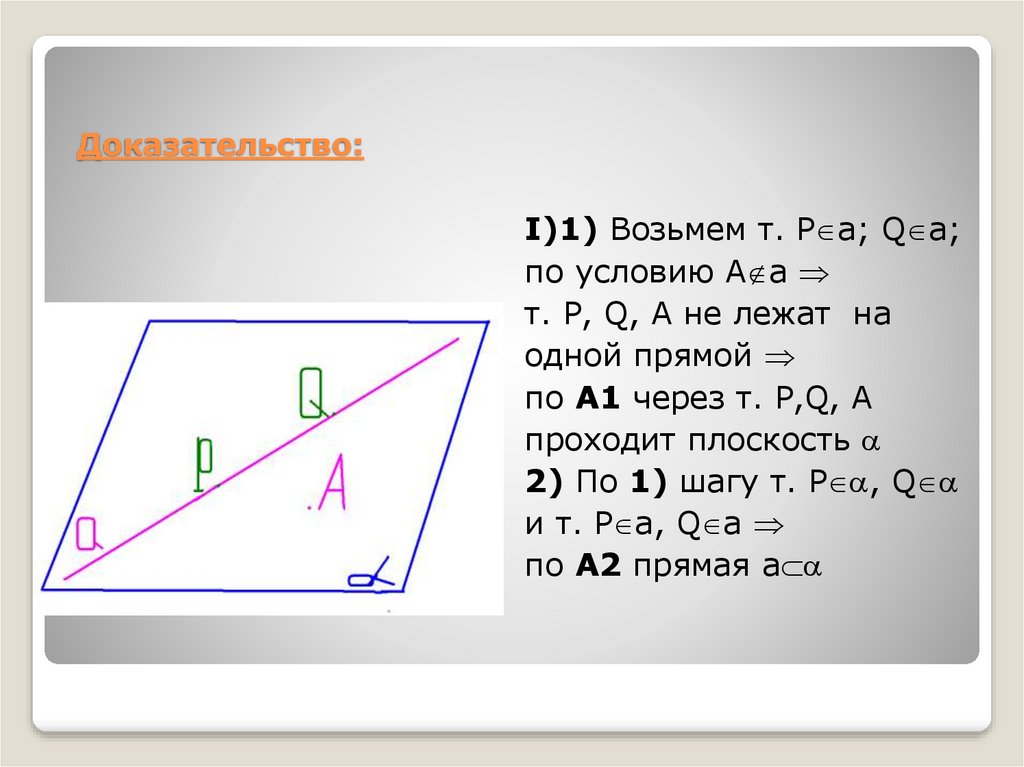
3. Доказательство:
Ι)1) Возьмем т. Р a; Q a;по условию А a
т. Р, Q, А не лежат на
одной прямой
по А1 через т. Р,Q, А
проходит плоскость
2) По 1) шагу т. Р , Q
и т. Р a, Q a
по А2 прямая a
4.
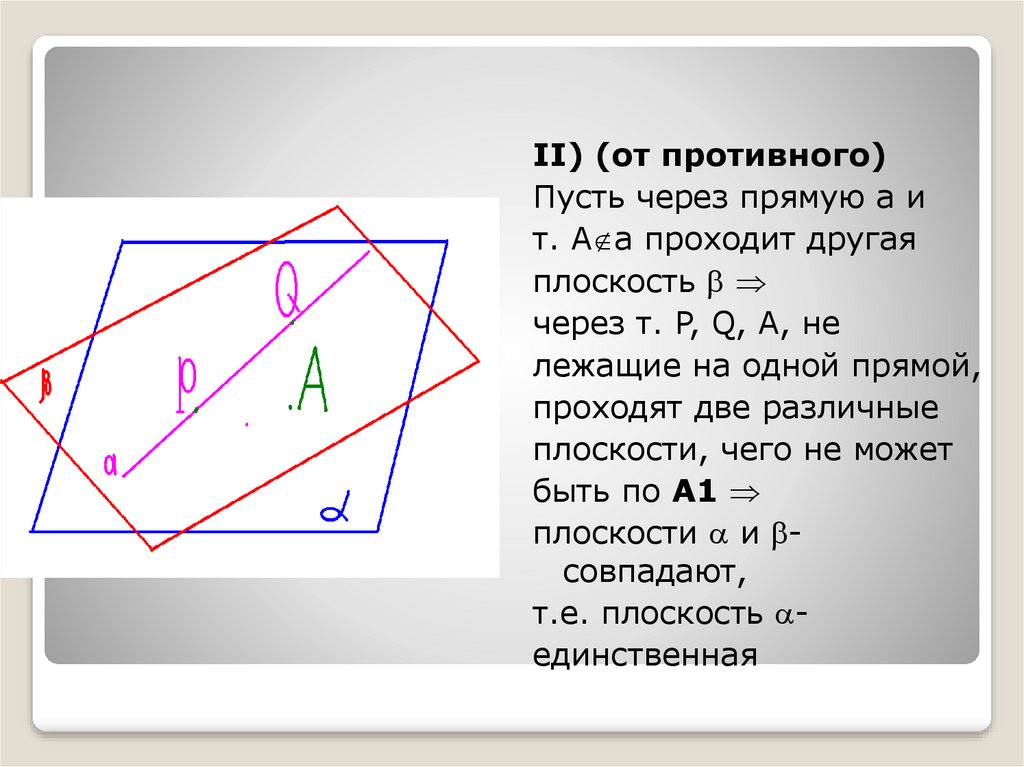
ΙΙ) (от противного)Пусть через прямую a и
т. А a проходит другая
плоскость
через т. P, Q, A, не
лежащие на одной прямой,
проходят две различные
плоскости, чего не может
быть по А1
плоскости и совпадают,
т.е. плоскость единственная
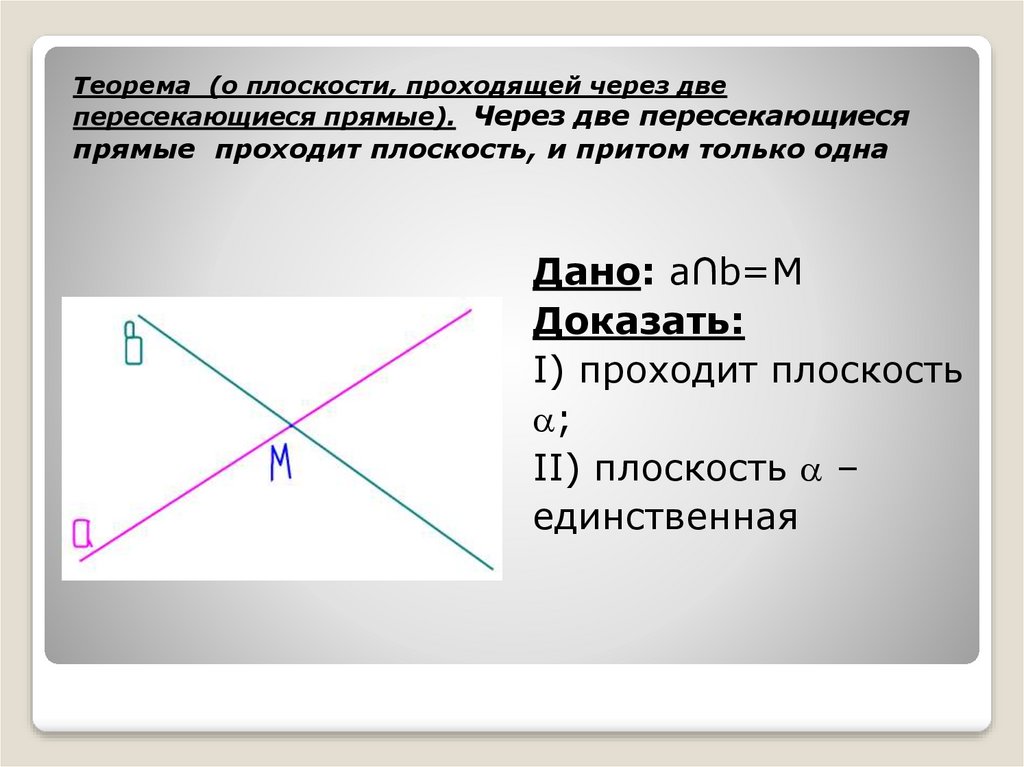
5. Теорема (о плоскости, проходящей через две пересекающиеся прямые). Через две пересекающиеся прямые проходит плоскость, и притом
только однаДано: a∩b=М
Доказать:
Ι) проходит плоскость
;
ΙΙ) плоскость –
единственная
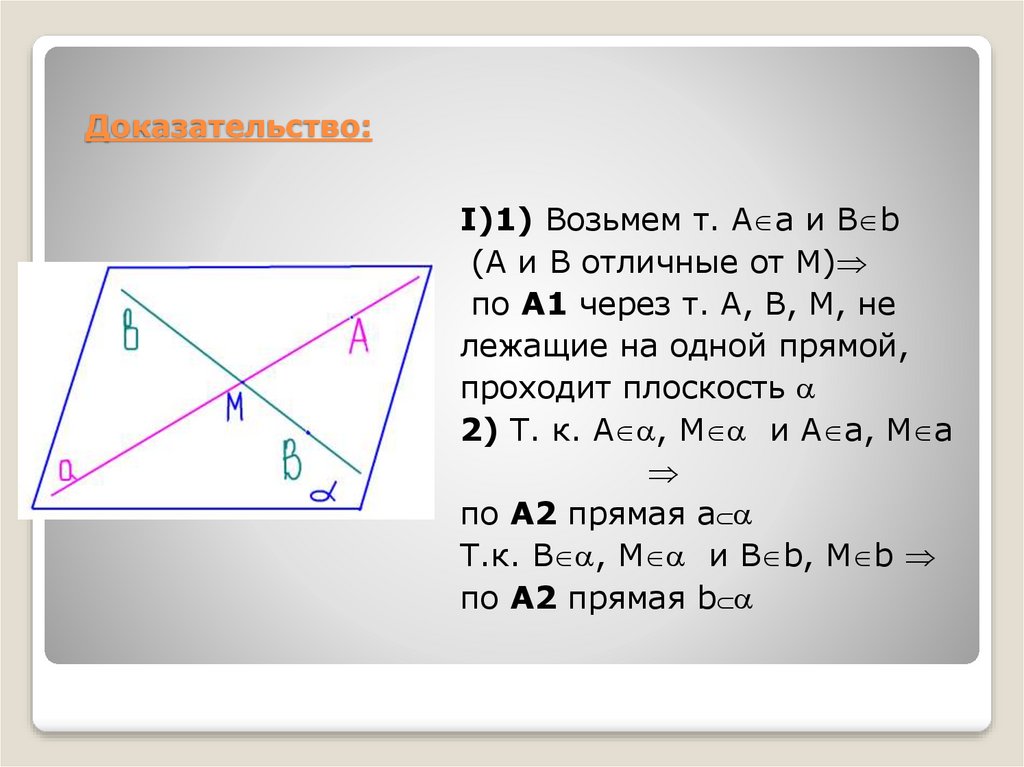
6. Доказательство:
Ι)1) Возьмем т. А a и В b(А и В отличные от М)
по А1 через т. А, В, М, не
лежащие на одной прямой,
проходит плоскость
2) Т. к. А , М и А a, М a
по А2 прямая a
Т.к. В , М и В b, М b
по А2 прямая b
7.
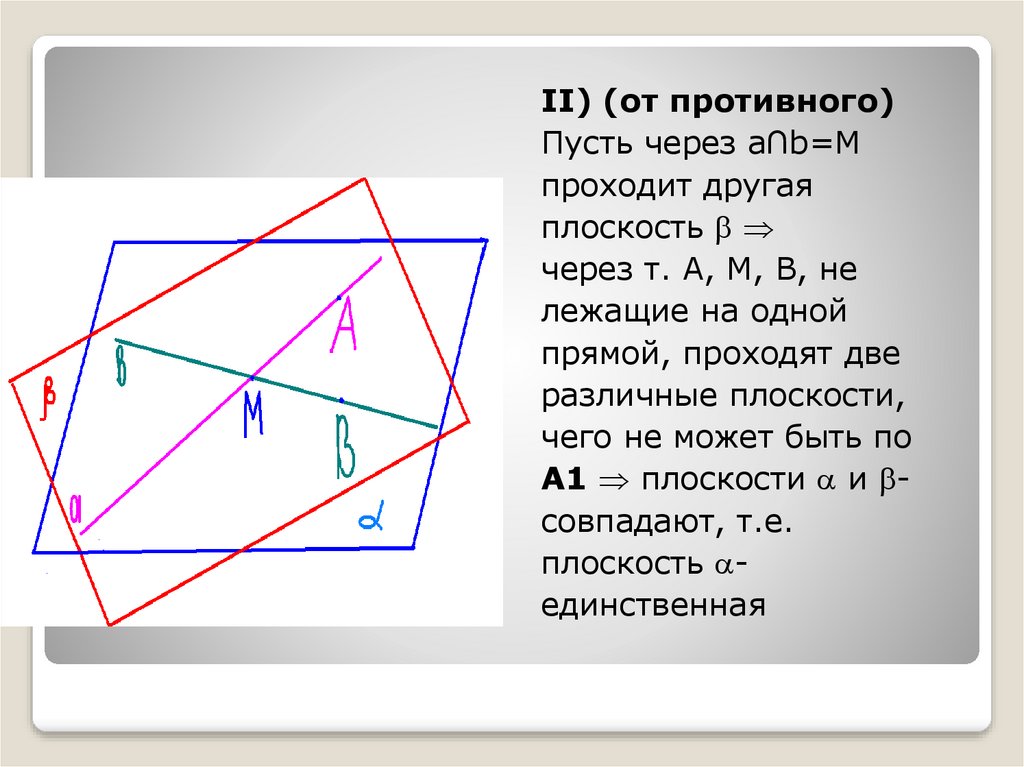
ΙΙ) (от противного)Пусть через a∩b=М
проходит другая
плоскость
через т. А, М, В, не
лежащие на одной
прямой, проходят две
различные плоскости,
чего не может быть по
А1 плоскости и совпадают, т.е.
плоскость единственная


 Математика
Математика








