Свойства чисел

1.

2.

Могут ли числа 1234567897 и 1234567892 быть квадратами
каких-либо целых чисел?

3.

Вычеркните в числе 23462141 три цифры так, чтобы
получившееся число делилось на 12.

4.

Общий признак делимости на составное число: Пусть a –
составное число, являющееся произведением двух взаимно
простых чисел b и с: а = bс. Тогда число n делится на а тогда,
когда n делится и на b, и на с.
Отсюда следует, что на 12 делятся те числа, которые делятся и на 3,
и на 4 (но не на 2 и на 6, так как 2 и 6 не взаимно простые числа).

5.

Приведите пример четырёхзначного числа, кратного 12,
произведение цифр которого равно 10.

6.

Приведите пример трёхзначного натурального числа, большего 600, которое при делении на 4, на 5 и на 6 даёт в остатке 3 и цифры которого расположены в порядке убывания
слева направо. В ответе укажите ровно одно такое число.

7.

Если число n делиться на a, на b, на с и т.д., то оно будет
делиться на НОК(a, b, c, …).

8.

9. Найти верную запись:

1)
2)
3)
4)
5)
6)
968845 ⋮ 2
940394 ⋮ 3 = 2
234345 ⋮ 15 = 17
115122 : 7 = 16446
894588 ⋮ 4 = 1
984500 ⋮ 6

10. Найти верную запись:

18756 ⋮ 4
18756 ⋮ 3
18756 ⋮ 12
18756 ⋮ НОК (4, 3)
n⋮6
5) ቊ
→ n ⋮ 12
n⋮2
1)
2)
3)
4)
n⋮6
6) ቊ
→ n ⋮ НОК (6, 2)
n⋮2

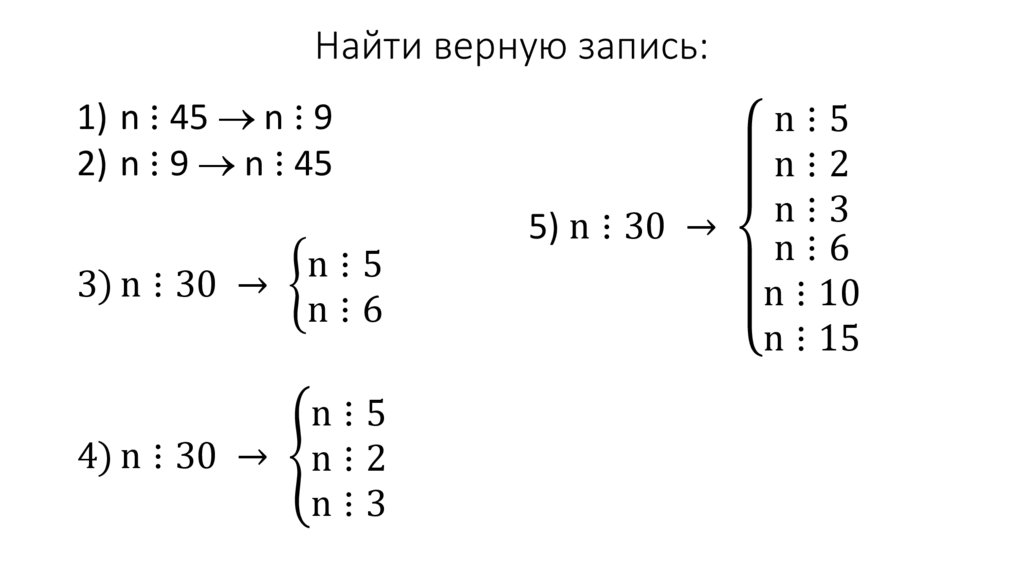
11. Найти верную запись:

1) n ⋮ 45 n ⋮ 9
2) n ⋮ 9 n ⋮ 45
n⋮5
3) n ⋮ 30 → ቊ
n⋮6
n⋮5
4) n ⋮ 30 → ቐn ⋮ 2
n⋮3
5) n ⋮ 30 →
n⋮5
n⋮2
n⋮3
n⋮6
n ⋮ 10
n ⋮ 15

12. Найти верную запись, используя правило деления на составное число:

n⋮5
1) ቄ
→ n ⋮ 30
n⋮6
n⋮5
2) ቐn ⋮ 2 → n ⋮ 30
n⋮3
n ⋮ 15
3) ቊ
→ n ⋮ 30
n⋮6
n⋮5
n⋮2
n
⋮
3
4)
→ n ⋮ 30
n⋮6
n ⋮ 10
n ⋮ 15

13.

1. ቊ
n⋮6
¬ n ⋮ 12
n⋮2
2. ቊ
n⋮6
↔ n ⋮ НОК 6, 2
n⋮2
n⋮5
3. ቐn ⋮ 2 ↔ n ⋮ 30 ↔ НОК (5, 2, 3)
n⋮3
Т.к. 6 и 2 не взаимно простые числа,
то n будет кратно ТОЛЬКО НОК (6, 2)
Т.к. 5, 2, 3 – взаимно простые числа,
то n будет кратно и произведению
5*2*3 и НОК(5, 2, 3)

14.

15.

Найдите трёхзначное число, у которого ровно две цифры
одинаковые, если известно, что оно даёт одинаковые
остатки при делении на 2 и на 5, а также известно, что сумма
его цифр равна 11. В ответе укажите какое-нибудь одно
такое число.

16.

Приведите пример такого трехзначного числа, которое при
делении на 29 и 31 даёт равные ненулевые остатки, и
первая цифра которого в три раза больше последней цифры.