Похожие презентации:
Иілу деформациясының потенциалдық энергиясы. Кастильяно теоремасы Мор интегралы Күштердің толық жұмысы
1.
2. Жоспары:
1.Ығысу. Ығысу түрлері:Бастапқы контурдың ығысуы,бұрыштық ығысу, бүйірлік
ығысу, білікаралық ығысу, құрал центрінің ығысуы,
салыстырмалы ығысу, таза ығысу, түзілімнің ығысуы.
2.Иілу. Иілу кезіндегі орын ауыстыру
ИІЛУ ДЕФОРМАЦИЯСЫНЫҢ ПОТЕНЦИАЛДЫҚ ЭНЕРГИЯСЫ
Кастильяно теоремасы
Мор интегралы
Күштердің толық жұмысы
3. Пайдаланылған әдебиеттер
3.
Ығысу– материалдар кедергісінде түскен күшәсерінен серпімді денелердің
өзара параллель қабаттарының
(талшықтарының) аралық қашықтығын
өзгертпей формациясын ауыстыруы. Мысалы,
тік төртбұрышты білеудің үстіңгі қырына оның
табанына (жылжымастай бекітілген)
параллель бағытталған күшпен әсер еткенде,
білеу ығысуының формациясы өзгереді сс1dd1 жылжу
шамасы абсолюттік ығысуды, бұрышы салысты
рмалы ығысуды анықтайды. Егер білеудің
қырына тек жанама кернеу ғана әсер етсе ол
таза ығысу деп аталады.
4. Түрлері
Бастапқы контурдың ығысуы (Смещение исходного контура) —берілістегі кепілді бүйір саңылауын қамтамасыз ету үшін бастапқы
контурды номиналдық күйінен тісті доңғалақтың денесіне қарай
қосымша ығыстыру.
Бұрыштық ығысу (Смещение угловое) — бұрыштардың номиналдық
күйінен ығысуы.
Бүйірлік ығысу (Смещение боковое) — бастапқы контурды
номиналдық күйінен бүйіріне қарай ығыстыру.
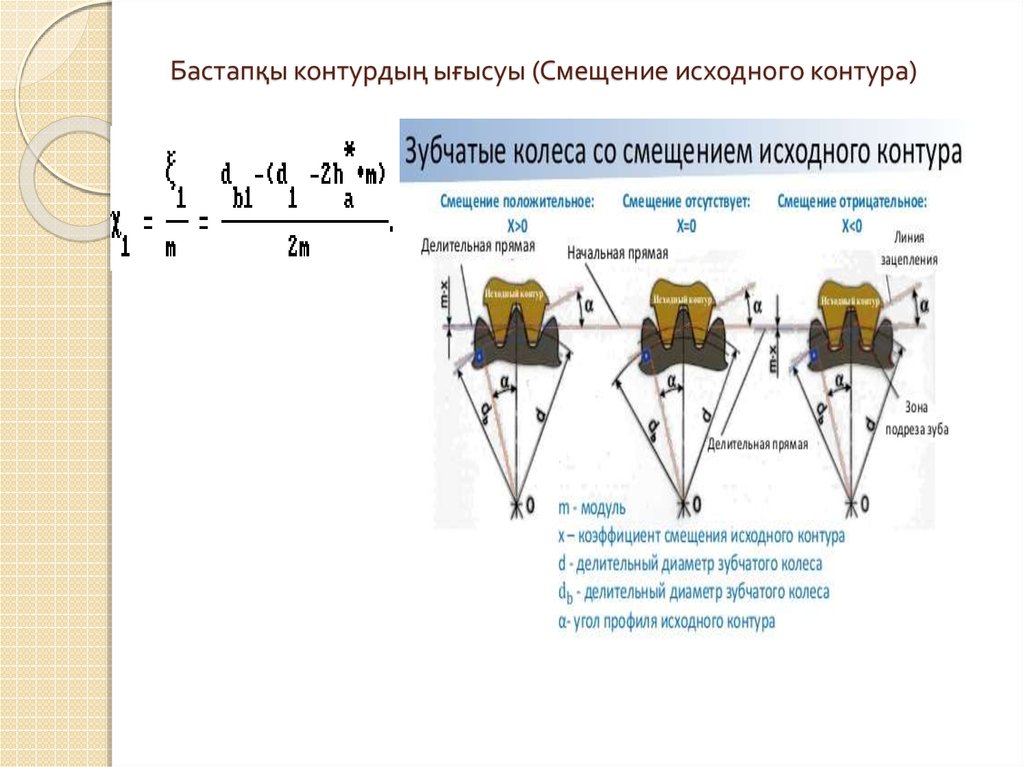
Білікаралық ығысу (Смещение между валами) — біліктердің
номиналдық күйінен ығысуы.
Құрал центрінің ығысуы (Смещение центра инструмента) — құрал
центрінің номиналдық күйінен ығысуы.
Салыстырмалы ығысу (Сдвиг относительный) — ығысу
деформациясын сипаттайтын бұрыш.
Таза ығысу – жазық кернеулі күйдің жеке бір түрі. Болаттардың,
тойтарма шегелердің, электрлік пісірумен бекітілген жіктердің
ығысуға беріктілігі сыналып отырады.
Түзілімнің ығысуы (Смещение узла) — түзілімнің номиналдық күйінен
ығысуы.
5.
Ығысу жазықтығы (Плоскость сдвига) — кесіліпжатқан қабаттың ағызба жаңқаға айналу процесі
кезіңде оның түрін бүзбай, өңделіп отырған
материалдың жүқа қабаттарының бірізділік
ығысуы болатын жерді — шартты ығысу дейді.
Ығысу кернеуі (Напряжение сдвига) — металга
түскеңде ығысуды жүргізетін кернеу.
Ығысу модулі (Модуль сдвига) — жанама
кернеудің жөне осы жанама кернеу әсер еткенде
пайда болатын шартты деформацияның
қатынасымен анықталатын ығысу.
Ығысу шегі (Предел при сдвиге) — материалды
қирауға дейін жеткізген ығысу деформациясы.
6. Бастапқы контурдың ығысуы (Смещение исходного контура)
7. Бұрыштық ығысу (Смещение угловое) — бұрыштардың номиналдық күйінен ығысуы.
8. Бүйірлік ығысу (Смещение боковое) — бастапқы контурды номиналдық күйінен бүйіріне қарай ығыстыру.
9. Білікаралық ығысу (Смещение между валами) — біліктердің номиналдық күйінен ығысуы.
10. Құрал центрінің ығысуы (Смещение центра инструмента)
11. Салыстырмалы ығысу (Сдвиг относительный) — ығысу деформациясын сипаттайтын бұрыш.
12. Таза ығысу
Таза ығысу — жазық кернеулі күйдің жекебір түрі. Жалпы жағдайда, жазық
кернеулі күйдің басты кернеулері келесі
формуламен анықталады
max
min
x y
Таза ығысу үшін
max
min
2
1
2
y 4
2
x
x y 0
немесе
1 , 3 .
2
13.
Абсолют ығысу үшін Гук заңын алуға болады.Qa
s a a
Q
CF
Таза ығысу деформациясының потенциалдық энергиясы
sQ
Q2a
u
2
2GF
Меншікті потенциалдық энергиясы
u
Q2a
Q2
2
uм
.
2
V 2GFaF 2GF 2G
14. ИІЛУ және ИІЛУ КЕЗІНДЕГІ ОРЫН АУЫСТЫРУ
15. ИІЛУ кезіндегі орын ауыстыру
Бойлық ось арқылы өтетін жазықтықтарда (осьжазықтықтарында) жатқан көлденең күштер мен
моменттердің (қос күштердің) әсерінен бруста пайда
болған деформацияны иілу деп атайды.
Иілу мөлшері деп, қима ауырлық центрінің бойлық
оське перпендикуляр бағытта (У осіне параллель)
орын ауыстыру шамасын айтады.
Ауырлық центрі абсцисса осінен жоғары қарай орын
ауыстырса иілу мөлшері оң, ал төмен қарай орын
ауыстырса теріс таңбалы деп қарастырылады.
16.
Берілген теңдеулер арқылыdy
EI x EI x
M ( z )dz C
dx
ІХ.04,
ІХ.03,
EI x y dz M ( z )dz Cz D
Тұрақты шамалар белгілі болса, (ІХ.03, ІХ.04)
теңдіктерін пайдаланып, кез келген қиманың
бұрылу бұрышы мен иілу мөлшерін анықтауға
болады.
17. ИІЛУ ДЕФОРМАЦИЯСЫНЫҢ ПОТЕНЦИАЛДЫҚ ЭНЕРГИЯСЫ
Июші момент өзі жатқан қиманы қаңдай да бірбұрышқа бұрып жұмыс жасайды
A
1
M .
2
Ішкі ию моментінің жұмыс шамасы сыртқы
моменттердің жұмыс шамасына тең, бағыттары
қарама-қарсы
1
Aiк M .
2
18.
Сол сияқты шамасы dМ-ге тең ішкі моменттіңжұмысы :
1
dAiк Md .
2
Еңді d dz / , 1/ M / EI x екеңдігін ескерсек ,
Aiк
1
2
l
0
M2
dz
EI x
Сонда иілу деформациясының потенциалдық
энергиясы бұлай анықталады:
l
1 M2
U Aiк
dz.
2 0 EI x
19. ДЕФОРМАЦИЯНЫ ЭНЕРГЕТИКАЛЫҚ (ЖАЛПЫ) ӘДІСТЕРМЕН АНЫҚТАУғы иілу деформациясы
Сыртқы күш әсерінен жүйе нүктелерініңорын ауыстыру шамаларын
(деформацияларын) анықтау — күрделі
мәселелердің бірі.
Деформацияларды анықтайтын әдістердің
көпшілігі энергияның сақталу заңына
негізделген. Сондықтан, олар
энергетикалық әдістер деп аталады.
Механикада энергетикалық әдістерді
жалпы әдістер деп те атайды. Өйткені, бұл
әдістермен конструкция элементтерінің
кез келген деформацияларын анықтауға
болады.
20.
Конструкция элементі уақытқабайланысты баяу өзгеретін сыртқы күштің
әсерінен тепе-теңдік күйін жоғалтпаса,
онда күштің жұмысы деформацияның
потенциалдық энергиясына айналады.
Деформацияның потенциалдық
энергиясын U, ал сыртқы күштің жұмысын
Ар арқылы белгілейік. Энергияның
сақталу заңы бойынша
U = Ap
21.
Деформацияның потенциалдықэнергиясына, теріс таңбалы ішкі күштің
жұмысы сәйкес келеді:
U = –Aik немесе Ар = – Aik осыдан Ар + Аik =
0 екенін көреміз.
Ығысу деформациясы үшін:
1
1
Q 2 dz
U Ap Q s
,
2
2GF
0
Бұралу деформациясы үшін :
1
1
M 2 dz
U Ap M 0
,
2
2GIp
0
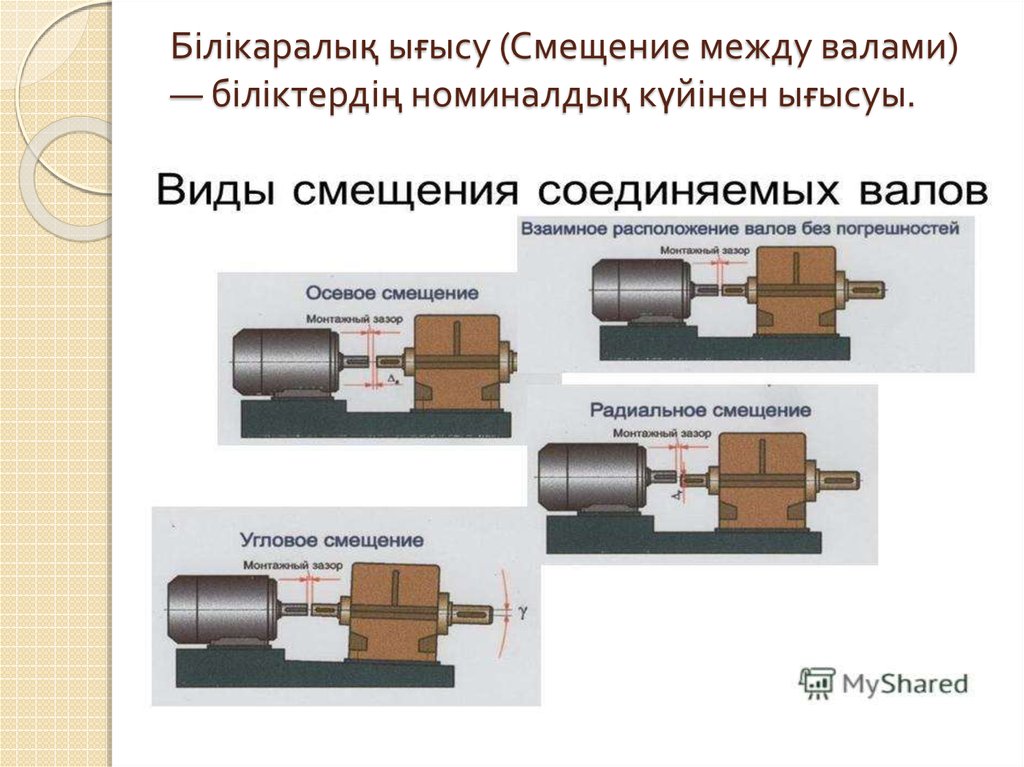
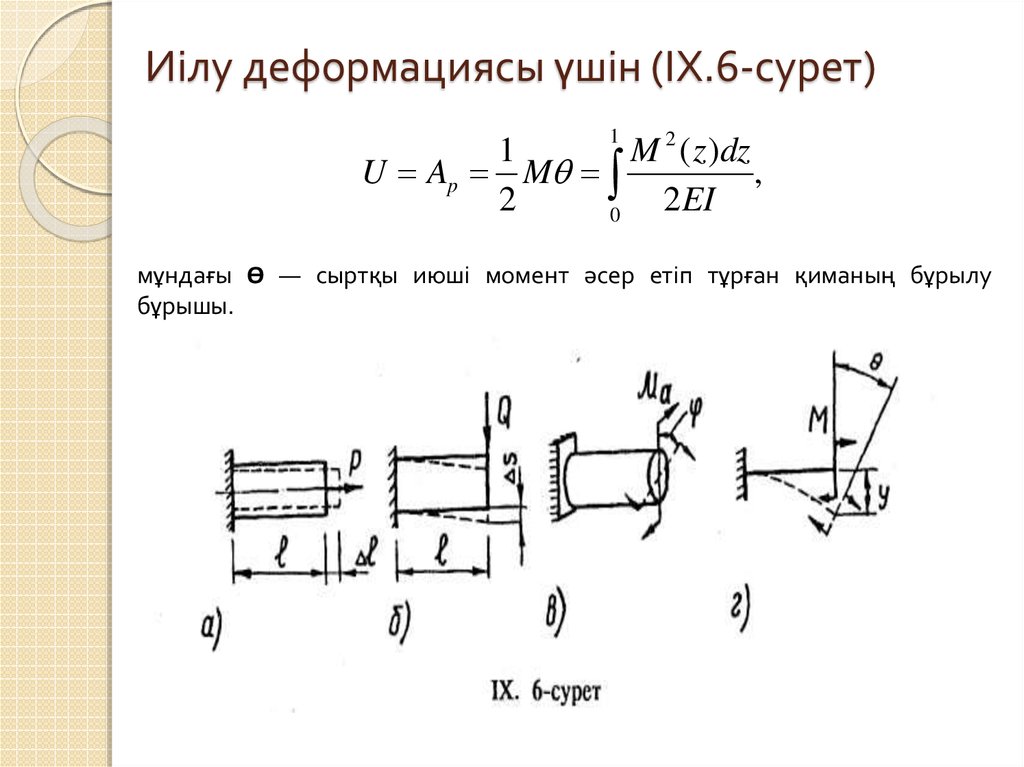
22. Иілу деформациясы үшін (ІХ.6-сурет)
11
M 2 ( z )dz
U Ap M
,
2
2EI
0
мұндағы Ө — сыртқы июші момент әсер етіп тұрған қиманың бұрылу
бұрышы.
23.
Жүйеге көп күштер әсер еткендедеформацияның потенциалдық энергиясы
Клапейрон формуласымен анықталады:
1
1
U A P1 1 P2 2 ...,
2
2
бірнеше жалпылама күштер әсерінен жүйеде
пайда болған деформацияның потенциалдық
энергиясы, жалпылама орын ауыстырулар мен
жалпылама күштердің көбейтінділерінің
қосындыларының жартысына тең.
24. Кастильяно теоремасы
Берілген арқалық Р1,Р2 күштерінің әсерінен иіледі. Күш әсереткен қималардагы иілу мөлшерін у1,у2 арқылы белгілесек,
1
1
P1 y1 P2 y2 .
2
2
dU
dP1
dP-күшінің орнына dM - ді қарастырып, киманың бұрылу
бұрышын табуға болады
U A
y1
U
M
Сонымен, потенциалдық энергиядан жалпылама күш бойынша алынған
туынды жалпылама орын ауыстыруга тең. Бұл теорема Кастильяно
теоремасы деп аталады.
25. Мор интегралы
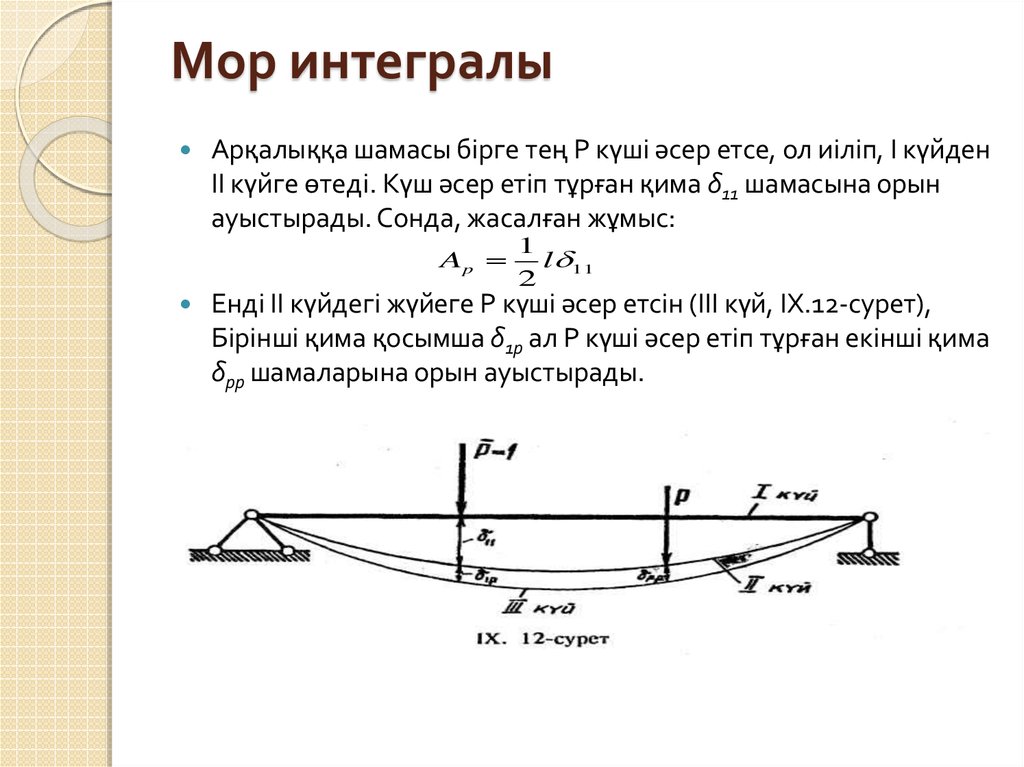
Арқалыққа шамасы бірге тең Р күші әсер етсе, ол иіліп, I күйденII күйге өтеді. Күш әсер етіп тұрған қима δ11 шамасына орын
ауыстырады. Сонда, жасалған жұмыс:
Ap
1
l 11
2
Енді II күйдегі жүйеге Р күші әсер етсін (III күй, ІХ.12-сурет),
Бірінші қима қосымша δ1p ал Р күші әсер етіп тұрған екінші қима
δpp шамаларына орын ауыстырады.
26. Күштердің толық жұмысы:
11
A l 11 P pp l 1 p ,
2
2
мұндағы (1/2)Р δpp — Р күшінің δpp шамасына
орын ауыстырғандагы жұмысы,
1 δ1p — шамасы бірге тең P күшінің δ1p
шамасына орын ауыстырғандағы жұмысы.
27. Деформацияның потенциалдық энергиясын ішкі күш арқылы өрнектесек
1(M p M )2
M 2 ( z )dz
U
dz
2 EI
2EI
0
0
1
мұндағы , M ( z) M p M , M — сыртқы Р күшінің
әсерінен қимада пайда болған ию моменті.
M — шамасы бірге тең күштің әсерінен қимада пайда
болған ию моменті.
p
28. Жақшаны ашсақ:
1U
M p2 ( z )dz
0
2EI
1
2M p Mdz
2EI
0
1
M 2 dz
2EI
0
осыдан,
1
2
1
M dz
l 11
,
2
2EI
0
l 11
1
0
1
M l
P
pp
M p2 dz
0
M p Mdz
EI
.
EI
29.
Сонымен, қиманың орын ауыстыру шамасынанықтау үшін сол қимаға (иілу мөлшерін
іздеген бағытта) шамасы бірге тең күш әсер
еткіземіз. Сыртқы күш Р мен шамасы бірге тең
күштерінің әсерінен қималарда пайда болған
ию моменттеріиің өрнектерін Мор
интегралына енгізіп интегралдап, иілу
молшерін (орын ауыстыру) анықтаймыз.
Арқалық бірнеше аралықтан тұрса, Мор
интегралы ию моментінің өзгеру заңдылығы
тұрақты әр аралық үшін жеке есептеліп,
нәтижелері қосылады.Қиманың бұрылу
бұрышын табу үшін сол қимаға шамасы бірге
тең момент әсер еткізіп, көрсетілген тәртіп
пен Мор интегралын анықтайды.
30. Верещагин әдісі
Мор интегралын А. Н, Верещагин ұсынғанәдіспен оңай есептеуге болады. Ол үшін
сыртқы және шамасы бірге тең күштердің
әсерлерінен қималарда пайда болған ию
моменттерінің эпюрлері пайдаланылады.
Бұл әдісті аталган эпюрлердің бірі түзу
сызықты болғанда ғана қолдануға
болады. Ал қалған екінші эпюр түзу
сызықты немесе қисық сызықты бола
беруі мүмкін.
31.
Верещагиннің әдісі бойынша қиманың бұрылу бұрышымен орын ауыстыру шамасы, әр аралықтардағы сыртқы
күштің ию моментінің эпюрінің ауданын сол эпюрдін
ауырлық центрінің тұсындағы бірлік ию моментінің
эпюрінің ординатасына көбейтіп, көбейтінділерін
қосқанға тең.
1 p
y
i
EI
ic
,
Верещагин әдісі эпюрлерді көбейту әдісі немесе
графикалық әдіс деп те аталады. Аралықтағы эпюр
күрделі болса, ол қарапайым фигураларға жіктеліп, әр
фигура үшін Верещагин әдісі жеке қолданылып,
нәтижелері қосылады.
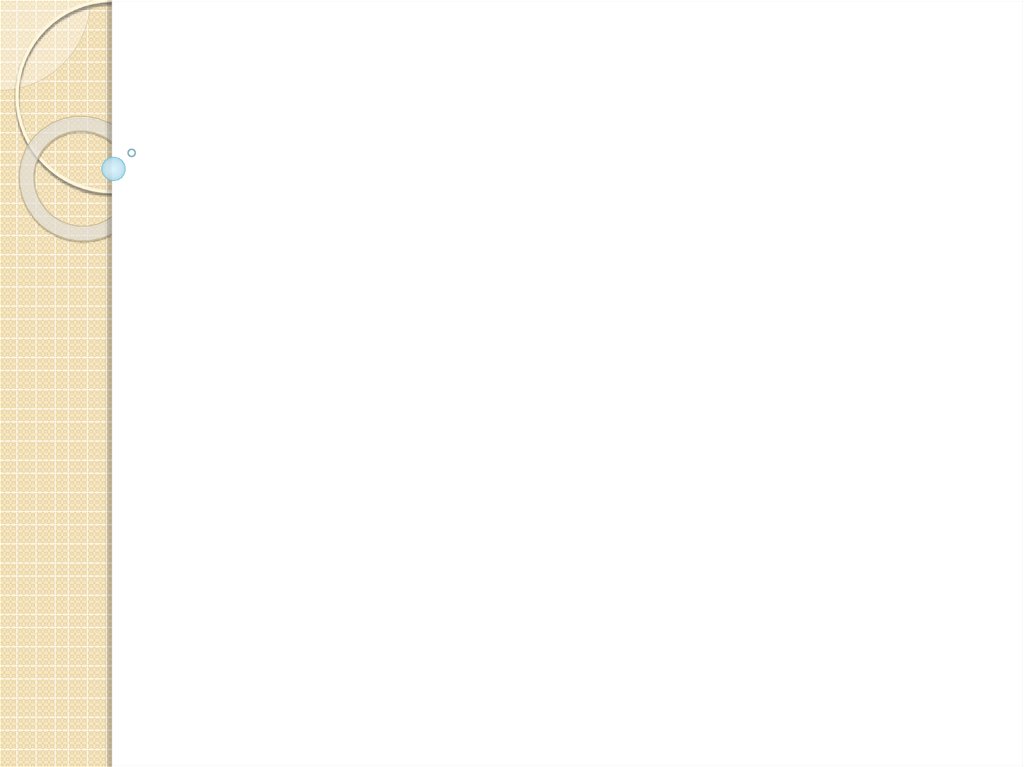



























 Физика
Физика








