Похожие презентации:
Теорема Чевы
1.
Теорема Чевы2.
Теорема Чевы (прямая)Пусть в ∆ABC на сторонах BC,AC,AB или их
продолжениях взяты соответственно точки A1, B1 и
C1,не совпадающие с вершинами треугольника.
Прямые A A1, BB1 и CC1 пересекаются в одной точке
или параллельны тогда и только тогда, когда
выполняется равенство
AC BA CB
1
1 1
C 1 B A1 C B1 A
1
3.
Доказательство
Предположим, что прямые АА1, ВВ1, СС1 пересекаются в
точке О.
Через вершину С треугольника ABC
проведем прямую, параллельную АВ, и ее точки
CB1 CB2
пересечения с прямыми AA1, BB1
.
обозначим соответственно А2, В2. Из подобия
B1A AB
1)
треугольников СВ2В1 и АВВ1 имеем равенство BA1
AB
Аналогично, из подобия треугольников ВАА1 и СА2А1
2)
имеем равенство
Далее, из подобия треугольников BC1Oи В2СО,
AC 1O и А2СО имеем
Следовательно, имеет место равенство (3)
Перемножая равенства (1), (2) и (3), получим
требуемое равенство
AB1 CA1 BC1
*
*
1.
B1C A 1B AC1
A 1C
A 2C
.
4.
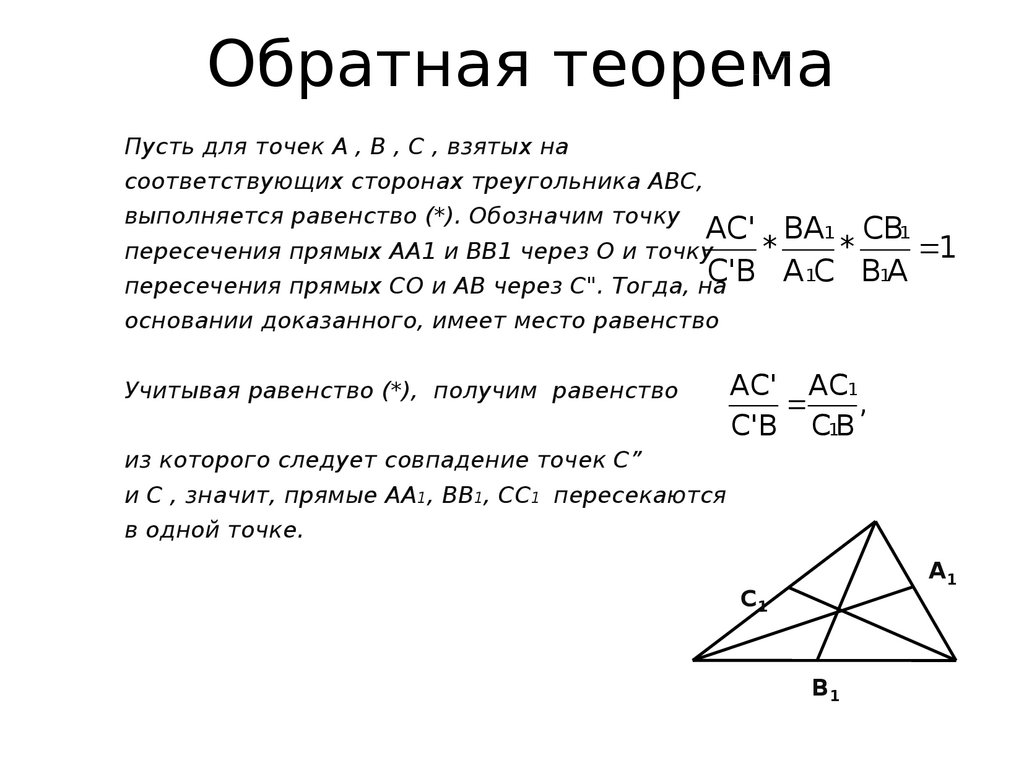
Обратная теоремаПусть для точек А , В , С , взятых на
соответствующих сторонах треугольника ABC,
выполняется равенство (*). Обозначим точку
AC' BA1 CB1
*
*
1
пересечения прямых АА1 и ВВ1 через О и точку
C'B A 1C B1A
пересечения прямых СО и АВ через С". Тогда, на
основании доказанного, имеет место равенство
Учитывая равенство (*), получим равенство
AC' AC1
,
C'B C1B
из которого следует совпадение точек С”
и С , значит, прямые АА1, BB1, СС1 пересекаются
в одной точке.
А1
С1
В1
5.
Следствия Теорема Чевы• Следствие1. Медианы треугольника пересекаются в одной
точке, которая делит каждую медиану в отношении 2:1,
считая от вершины.
• Следствие 2. Биссектрисы треугольника пересекаются в одной
точке.
• Следствие3. Высоты треугольника (или их продолжения)
пересекаются в одной точке.
6.
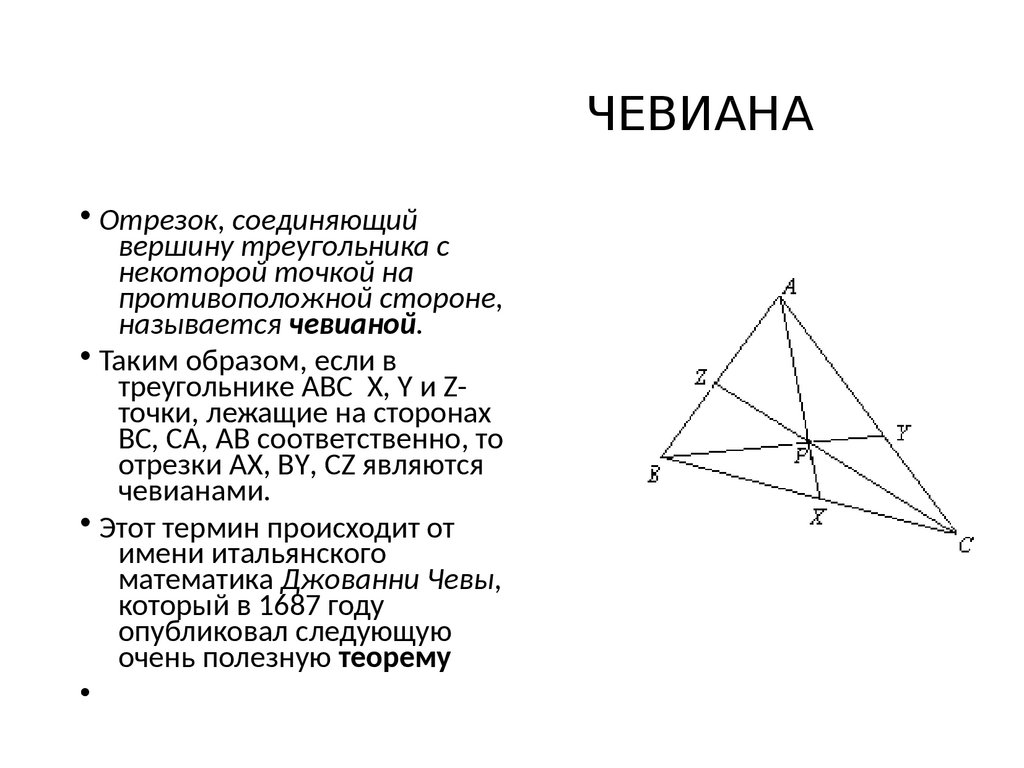
ЧЕВИАНА• Отрезок, соединяющий
вершину треугольника с
некоторой точкой на
противоположной стороне,
называется чевианой.
• Таким образом, если в
треугольнике АВС X, Y и Zточки, лежащие на сторонах
ВС, СА, АВ соответственно, то
отрезки АX, ВY, СZ являются
чевианами.
• Этот термин происходит от
имени итальянского
математика Джованни Чевы,
который в 1687 году
опубликовал следующую
очень полезную теорему
7.
Задача 1Дано:
АВС - треугольник,
Вписанная (или вневписанная)
окружность касается прямых
ВС, АС и АВ в точках А1,В1 и
С1.
Доказать:
что, прямые AA1, BB1 и CC1
пересекаются в одной точке.
8.
РешениеАВ1=АС1, ВС1 =ВА1,
и СА1 = СВ1, причем в случае
вписанной окружности на
сторонах треугольника АВС
лежат три точки, а в случае
вневписанной – одна точка.
Воспользовавшись теоремой Чевы, получим что
прямые AA1, BB1 и CC1 пересекаются в одной точке.
9.
Задача 2• На медиане АА1 треугольника АВС взята
произвольная точка М. Построены
точки В1 = ВМ ∩ СА,С1 = СМ ∩ ВА.
Докажите, что ВСВ1С1 – трапеция.
• (указания). Докажите, что АВ1 : В1С = АС1 :
С1В







 Математика
Математика








