Преобразование двойных радикалов

1. «Преобразование двойных радикалов»

Презентация нестандартного урока
по математике
«ПРЕОБРАЗОВАНИЕ
ДВОЙНЫХ РАДИКАЛОВ»
Класс: 8 «Б»
Учитель: Гареева Д.С.
МБОУ «Лицей №12»
г. Лениногорск, 2015

2. Цели урока:

• Рассмотреть методы преобразования,
выражений содержащих двойные
радикалы;
• Развивать логическое мышление учащихся,
путем группового изучения материала;
• Воспитывать коммуникабельность,
уважение друг к другу, умение доказывать
свое мнение и адекватно реагировать на
критику.

3. Задачи урока:

• Повторить пройденный ранее материал;
• Рассмотреть преобразование двойных радикалов с
помощью выделения полного квадрата;
• Изучить преобразование двойных радикалов с
помощью формулы;
• Разобрать метод избавления от иррациональности в
знаменателе для дробей содержащих двойные
радикалы;
• Развивать навыки индивидуальной, парной и
групповой работы.

4. Лучший способ изучить что-либо - это открыть самому.   

Девиз урока:
Лучший способ изучить
что-либо - это открыть самому.
Д. Пойа

5. Работа в парах

Повторить:
1. Как вынести множитель из-под знака
корня?
2. Как внести множитель под знак
радикала?
3. Как избавиться от иррациональности
в знаменателе или числителе дроби?

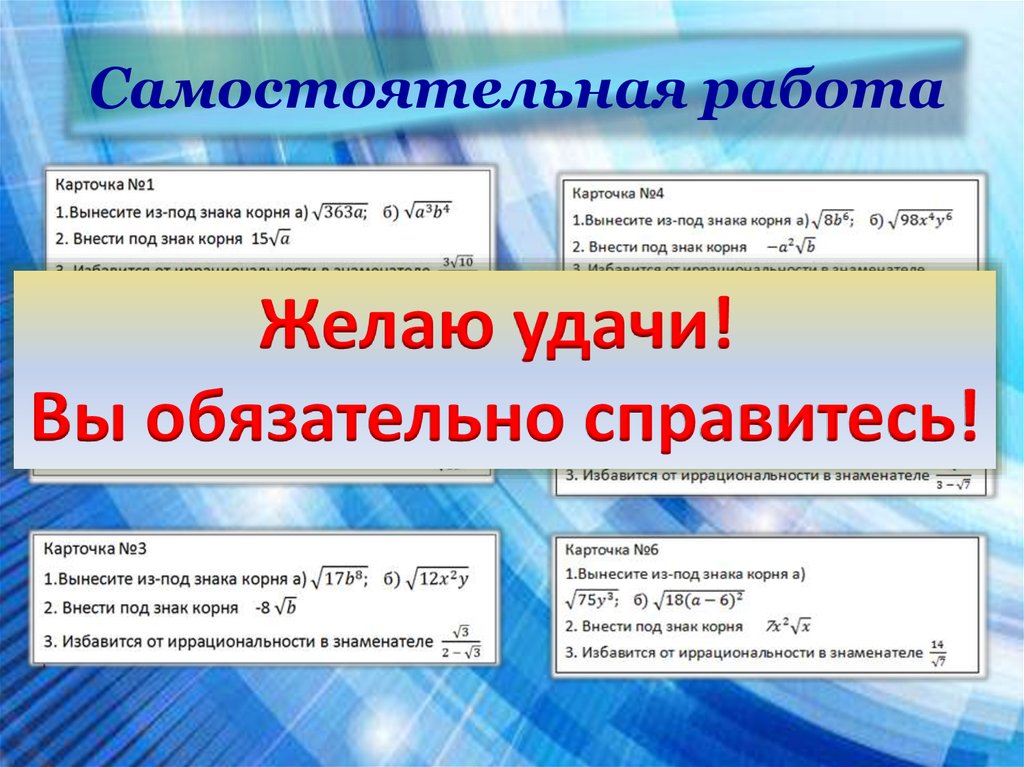
6. Самостоятельная работа

Желаю удачи!
Вы обязательно справитесь!

7. Вопрос дня:

Что – это ?….
Что с этим делать?...
Где это применить?...

8.

Тема урока:
«ПРЕОБРАЗОВАНИЕ
ДВОЙНЫХ РАДИКАЛОВ»

9. Групповая работа

• Задание – карточка
• Учебник – параграф 25, страница 160-161
• Подсказка – алгоритм выполнения задания
Группа №1
на карточке

10.

Группа №2
Группа №3
Группа №4
Группа №5

11.

Освобождение от внешнего радикала с
помощью выделения полного квадрата
Воспользуемся формулой полного
квадрата или квадрата суммы

12.

Освобождение от внешнего радикала с
помощью формулы двойного радикала
Запишем формулу двойного радикала
a
b
Определим коэффициенты a и b, преобразуем исходное выражение

13.

Произведем расчеты
Молодцы!
Проверить правильность результата можно,
возведя полученное выражение в квадрат.
Сделайте проверку!

14.

Освобождение от внешнего радикала с
помощью формулы двойного радикала
Избавимся от внешнего
радикала в знаменателе.
Отлично!
Домножим на сопряженное
знаменателю выражение.

15. Почему нельзя было домножить дробь на сопряженное выражение под корнем сразу?

Что нового ты узнал?
Где ты будешь применять
новые знания?
Стоит ли еще поработать над
этой темой?
Считаешь ли ты, что мы
достигли цели, поставленной в
начале урока ?

16. Домашнее задание

№560, №561, №564
Творческое задание: Докажите, что
если a 0, b 0, abc 4, то

17. Спасибо за урок!

Окончен урок, и выполнен план.
Спасибо, ребята, огромное вам.
За то, что упорно и дружно
трудились,
И цели намеченной с боем добились!