Похожие презентации:
Стационарные процессы теплопроводности
1.
СТАЦИОНАРНЫЕПРОЦЕССЫ
ТЕПЛОПРОВОДНОСТИ
1
2. ФУРЬЕ Жан Батист Жозеф 1768-1830
23. Коэффициент теплопроводности l, Вт/(м К)
Коэффициент теплопроводности , Вт/(м К)3
4. Механизм теплопроводности
В газах передача энергии осуществляется при столкновениичастиц, совершающих поступательное движение.
Из молекулярно-кинетической теории
1
сv L W
3
- плотность;
сv- теплоемкость;
L- средняя длина свободного пробега молекул;
W 3RT M
- средняя скорость молекул
(L ~ 1/P), ( ~ P).
Поэтому L. ~const
теплопроводность газов слабо зависит от давления.
воздух ~0,03 Вт/(м K)
4
5. Механизм теплопроводности
В жидкостях энергия переносится в процессеупругих столкновений колеблющихся частиц.
Из молекулярно-кинетической теории
p
ля обычных жидкостей:
A
c
А - коэффициент, пропорциональный
скорости упругих волн в жидкости;
М - молекулярный вес.
M
4/3
1/ 3
Для обычных, слабо ассоциированных жидкостей
t 0
и поэтому
вода ~0,6 Вт/(м K) при 20 оС,
t 0
натрий ~75 Вт/(м K) при 300 оС
5
6. Механизм теплопроводности
В твердых телах механизм переноса энергии связан с характеромтеплового движения атомов. Твердое тело - совокупность атомов,
совершающих колебания. Эти колебания не зависят друг от друга и
передаются (со скоростью звука) от одних атомов к другим.
ф e
Фононная составляющая так же, как и для газов:
1
c - скорость звука; L~1/T,
ф Cv L c
3
.
Электронная составляющая
e Lо T
Lо
2
ф ~ T 1
2
k - постоянная Лоренца;
3 e
k - постоянная Больцмана;
e - заряд электрона
- электропроводность
серебро ~430 Вт/(м K), медь ~400 Вт/(м K)
6
7. Механизм теплопроводности
Теплопроводность твердых неметаллическихматериалов зависит от: • структуры,
• пористости,
• влажности и т.д.
Пример:
сухой кирпич = 0,35 Вт/(м.К) ,
влажный = 1,0 Вт/(м.К)
Этот эффект связан
с конвективным переносом тепла и
.
с капиллярным движением жидкости внутри пор.
Теплоизоляционные материалы - коэффициент
теплопроводности менее 0,2 Вт/(м.К)
7
8.
Дифференциальное уравнение теплопроводностиУравнение сохранения энергии
для объема V,
ограниченного поверхностью F
Энергия,
подводимая
к V через F
F qdF
+
+
Энергия,
выделяемая
внутри V
V
qv dV
=
=
Энергия,
отводимая от
V через F
F qdF
+
+
Энергия,
аккумулируемая внутри V
Du
V d
8
9. Дифференциальное уравнение теплопроводности
Выражаем члены уравнения, обусловленные теплопроводностью,через закон Фурье
q dF ( gradt ) dF
F
F
Используем теорему Остроградского-Гаусса
о замене интеграла по поверхности интегралом по объему
от дивергенции
q
F
dF div(q ) dV div gradt dV
V
V
9
10. Дифференциальное уравнение теплопроводности
Подставляем в исходное уравнение энергииDu
d div gradt dV qv dV
V
V
V
Из термодинамики
Du с p dt d (PV )
Пренебрегаем изменением
давления и удельного объема
Du c p Dt
Dt
cp
div gradt qv
d
10
11. Дифференциальное уравнение теплопроводности
В декартовой системе координат2
2
2
t
t
t t t t
div gradt
x 2 y 2 z 2 x x y y z z
Субстациональная производная от функции для движущейся среды
D x y z
d
x y z
Dt t
t
t
t
Wx
Wy
Wz
d
x
y
z
11
12. Дифференциальное уравнение теплопроводности
Для постоянных свойств средыqv
Dt
2
a t
d
c p
, c p , const
a c p
Для твердого тела (неподвижной среды), W=0
qv
t
2
a t
c p
При отсутствии внутренних источников тепла
t
a 2 t
Для стационарного случая
2
t 0
12
13. Запись Лапласиана
В декартовых координатах2
t
2t
x
2
2t
y
2
2t
z
2
13
14. Запись Лапласиана
В цилиндрических координатах2
2
1
t
1
t
t
2
t
2
r 2
2
r r r r
z
или
2
2
1 t 1 t t
t 2
2
r r r 2 z 2
r
2
t
2
14
15. Запись Лапласиана
В сферических координатах1 2 ( rt )
1
t
t
2
sin
2
r r
r sin
2
1
2t
r 2 sin 2 2
или
2t
2
2
2
t
1
t
1
t 1
t
2
t 2
2 2
2 2 2 ctg
2
r r r sin
r
r
r
15
16. Условия однозначности
Условия однозначности - замыкающие соотношения,которые выделяют конкретную задачу из общего класса
задач
1. Геометрические условия
форма и размеры среды
,c p ,
2. Физические условия
свойства среды
3. Временные (начальные)
значения температуры в
начальный момент времени
t f x , y , z , 0
4.
Граничные условия
16
17. Граничные условия
Граничные условия требуют сопряжения температурных полей итепловых потоков на границах тела с окружающей средой:
I рода – задание на границе
распределения температуры:
в простейшем случае
t f1 x , y , z ,
t w const
II рода – задание на границе
плотности теплового потока:
t
q
f 2 x , y , z ,
n
т.е. задание распределения
градиента температуры на границе
III рода – задание условий
теплообмена
коэффициента теплообмена):
t
q
tw t f
n
17
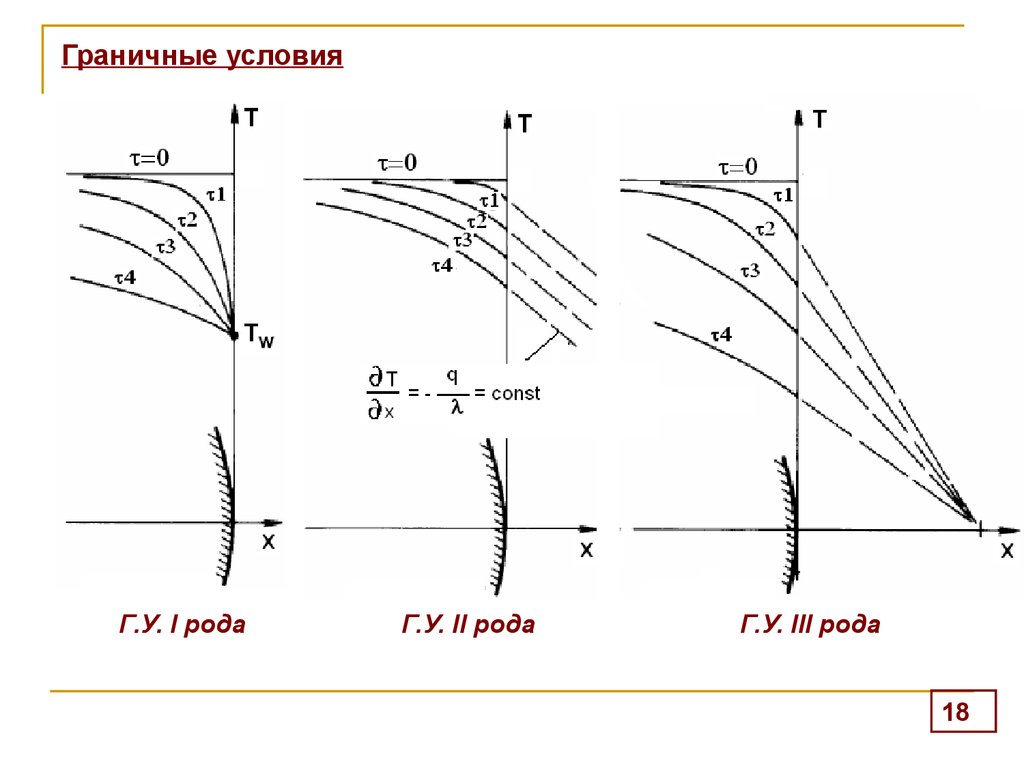
18. Граничные условия
Г.У. I родаГ.У. II рода
Г.У. III рода
18

















 Физика
Физика








