Стационарные процессы теплопроводности (продолжение)

1.

СТАЦИОНАРНЫЕ
ПРОЦЕССЫ
ТЕПЛОПРОВОДНОСТИ
(продолжение)
1

2. Дифференциальное уравнение теплопроводности

a
cp
Dt
cp
div gradt qv
d
qv
Dt
2
a t
d
c p
t
W grad t
d
изменение
изменение темп. поля,
температуры вызванное движением
во времени
среды
qv
a t
c p
2
изменение темп.
поля
в пространстве
интенсивность
внутренних
источников тепла
2

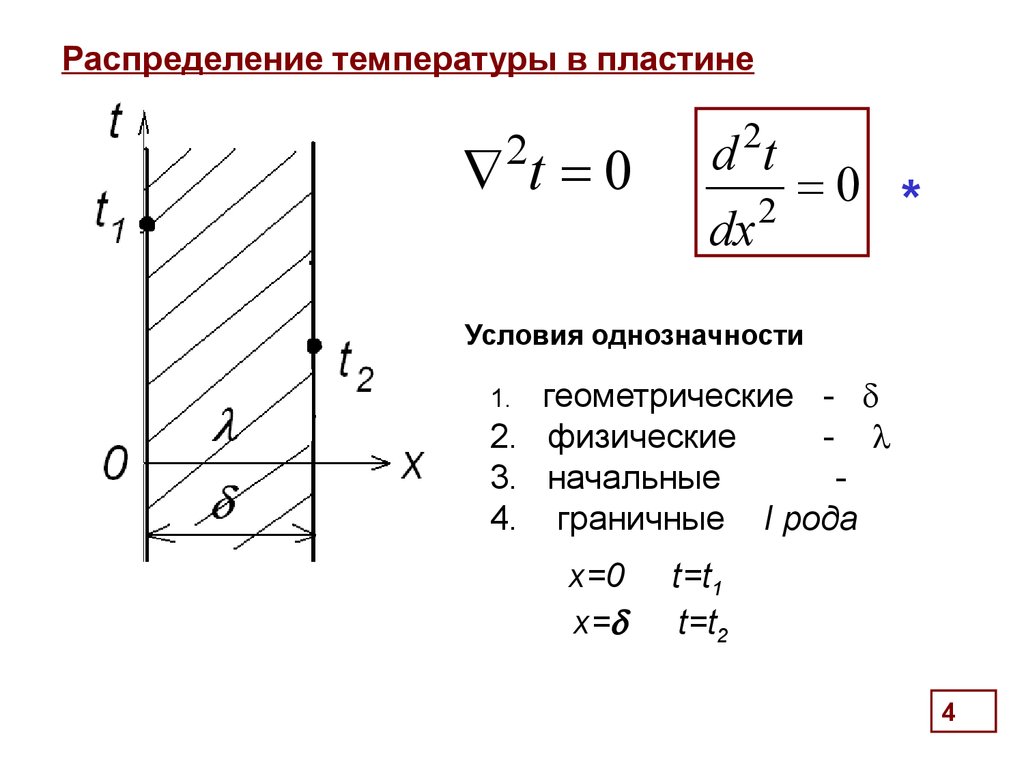
3. Распределение температуры в пластине

Найти:
стационарное распределение температуры
в пластине
без внутреннего тепловыделения
при Г.У. 1 рода
0
0
0
qv
t
2
W grad t a t
d
c p
стационарная
задача
неподвижная
среда
нет внутреннего
тепловыделения
3

4. Распределение температуры в пластине

2
t 0
2
d t
0
*
2
dx
Условия однозначности
геометрические -
2. физические
-
3. начальные
4. граничные I рода
1.
x=0 t=t1
x= t=t2
4

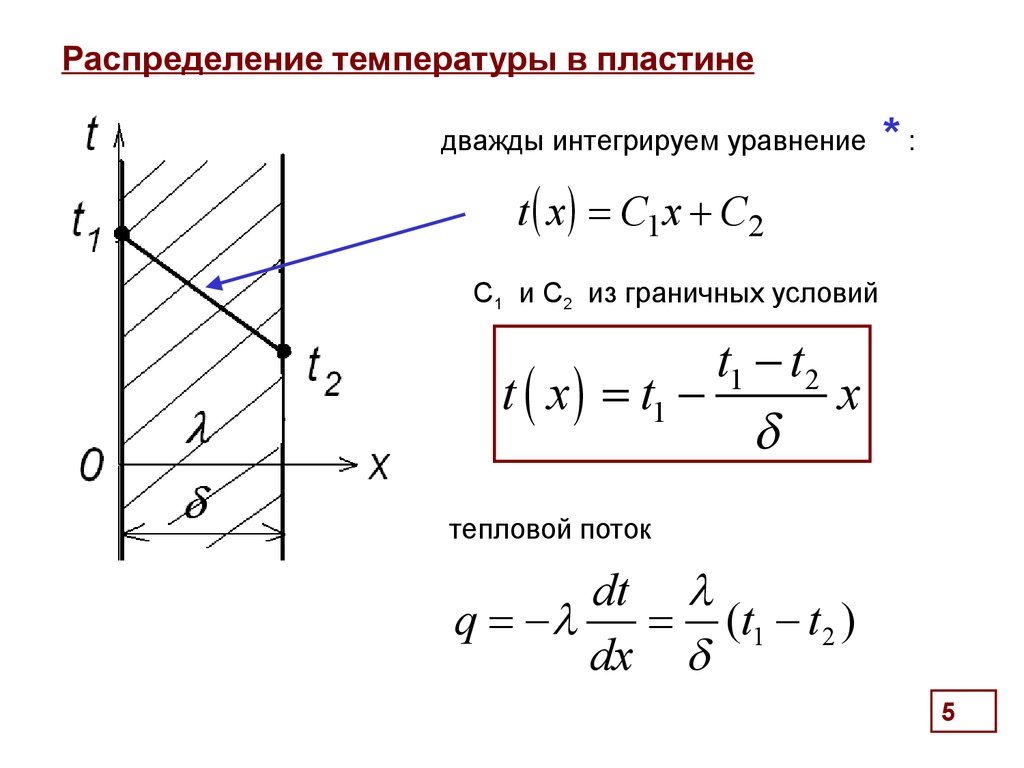
5. Распределение температуры в пластине

дважды интегрируем уравнение
*:
t x C1 x C2
С1 и С2 из граничных условий
t1 - t2
t x t1 x
тепловой поток
dt
q -
(t1 - t 2 )
dx
5

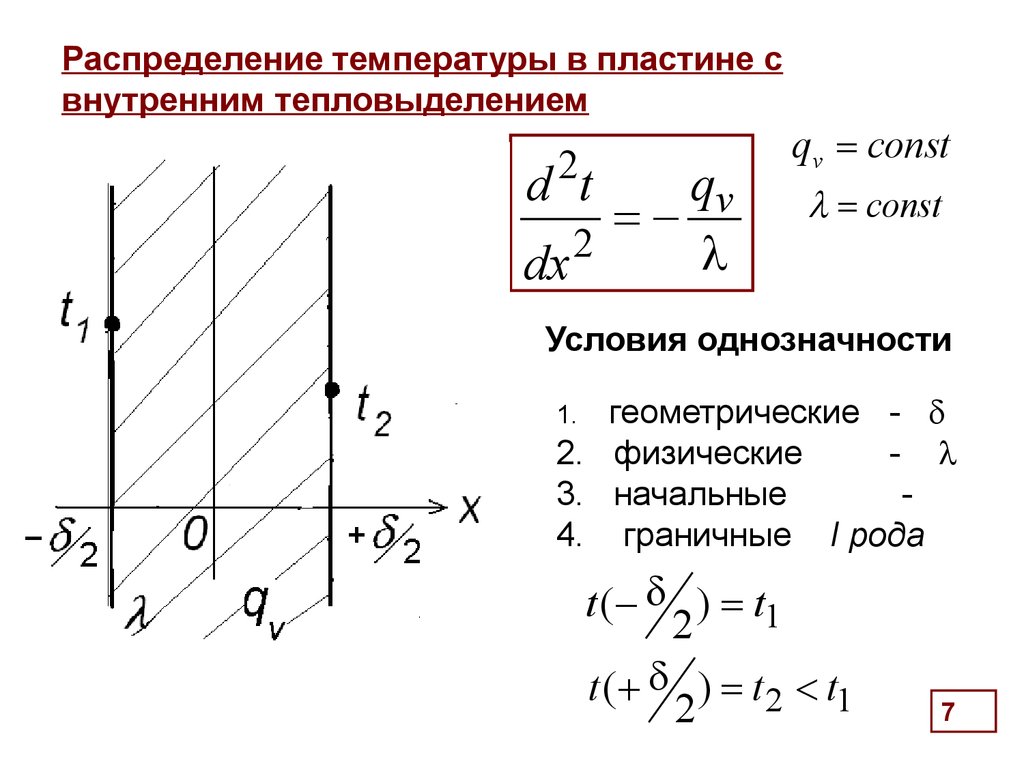
6. Распределение температуры в пластине с внутренним тепловыделением

Бесконечная плоская пластина толщиной с внутренними
источниками тепла q v Вт/м3, равномерно распределенными по
сечению
дифференциальное
уравнение
теплопроводности
qv
Dt
2
a t
d
c p
qv
t
2
W grad t a t
d
c p
2
t
2
t
x 2
2
t
y 2
2
t
z 2
температура
меняется в одном
направлении
6

7. Распределение температуры в пластине с внутренним тепловыделением

2
qv
2
dx
d t
qv const
const
Условия однозначности
геометрические -
2. физические
-
3. начальные
4. граничные I рода
1.
t (- ) t1
2
t ( ) t2 t1
2
7

8. Распределение температуры в пластине с внутренним тепловыделением

Последовательное интегрирование уравнения
дает:
2
 
qv x
t x C1x C2
2
Константы из граничных
условий:
t 2 - t1
C1
t 2 t1 qv 2
C2
2
8
2
t -t
qv
t1 t 2
2
2
1
- x
t x
x
2 2
2
8

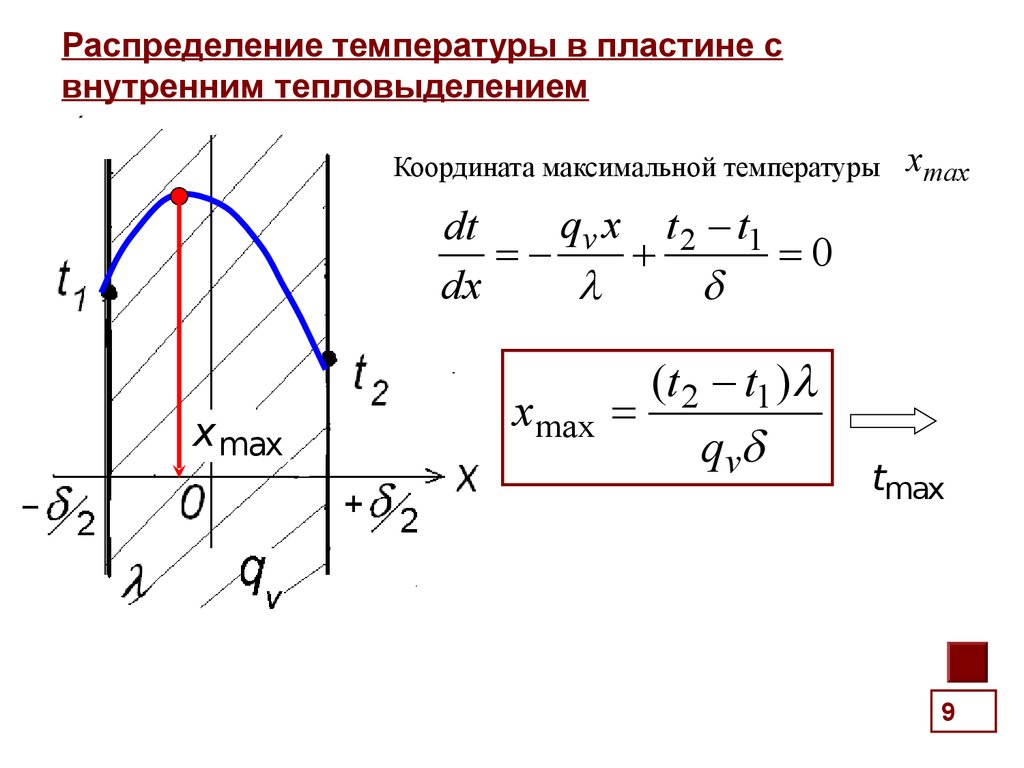
9. Распределение температуры в пластине с внутренним тепловыделением

Координата максимальной температуры
xmax
qv x t 2 - t1
dt
0
dx
x max
xmax
(t 2 - t1 )
qv
tmax
9

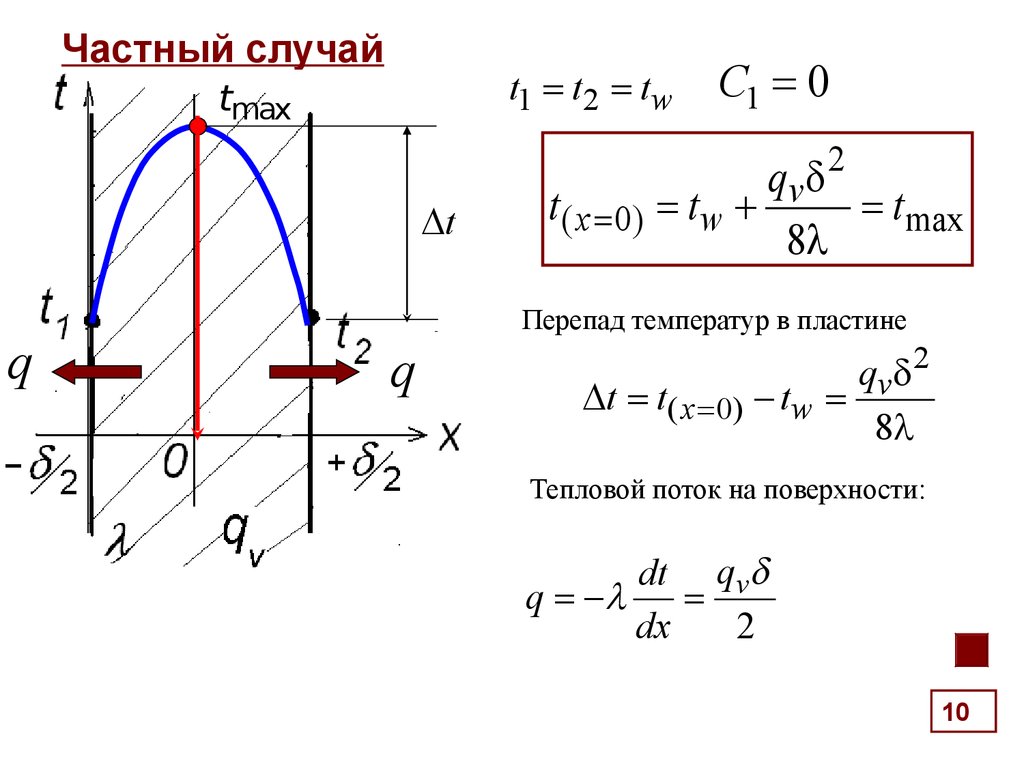
10. Частный случай

t1 t2 t w
tmax
t
q
C1 0
qv 2
t( x 0) t w
tmax
8
Перепад температур в пластине
q
qv 2
t t( x 0) - t w
8
Тепловой поток на поверхности:
dt qv
q -
dx
2
10

11. Распределение температуры в пластине с внутренним тепловыделением (Г.У. III рода)

заданы коэффициенты теплообмена на границах 1 , 2
и температуры жидкостей, омывающих поверхности
2
qv
2
dx
d t
t f1, t f 2
граничные условия III рода
dt
1( t f 1 - t )
dx - 2
dt
2( t - t f 2 )
dx 2
11

12. Распределение температуры в пластине с внутренним тепловыделением (Г.У. III рода)

решение уравнения:
qv x 2
t x C1x C2
2
1 qv 1 1
-
(tf 2 -tf1 ) 2 1 2
C1
1 1
1 2
Тепловой поток будет меняться в 
зависимости от координаты х:
dt
q -
qv x C1
dx
12

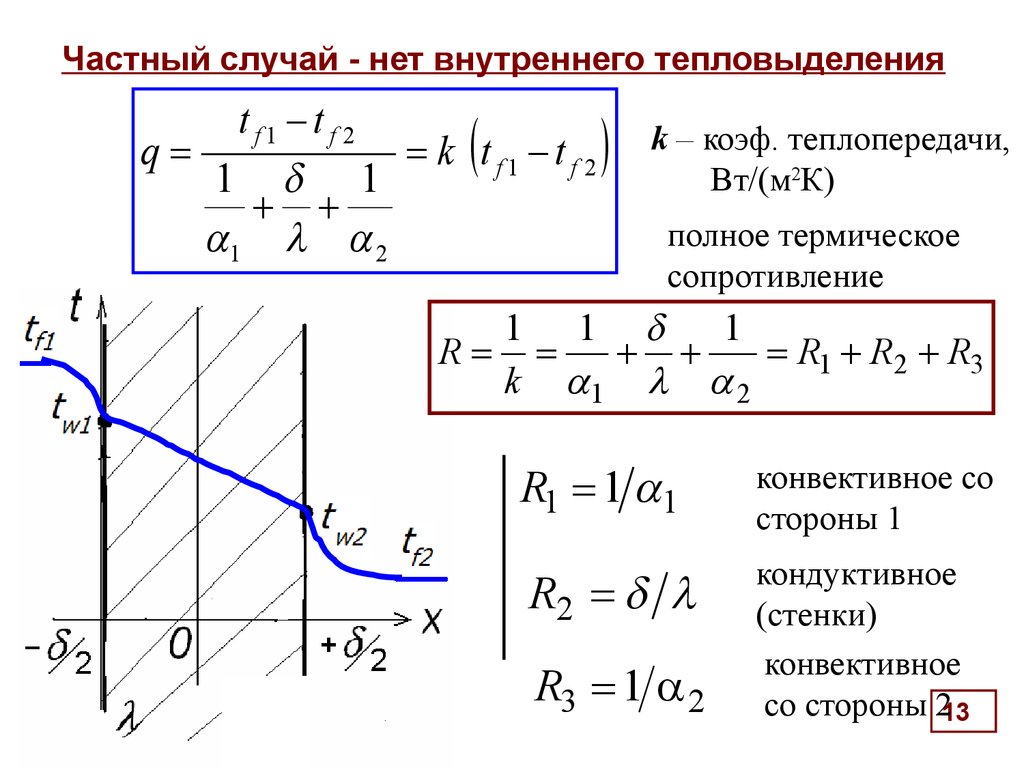
13. Частный случай - нет внутреннего тепловыделения

tf1 -tf 2
q
k t f 1 - t f 2 k – коэф. теплопередачи, 
       Вт/(м2К)
1 1
полное термическое 
1 2
сопротивление
1 1
1
R
R1 R2 R3
k 1 2
R1 1 1
конвективное со 
стороны 1
R2
кондуктивное 
(стенки)
конвективное 
со стороны 213
R3 1 2

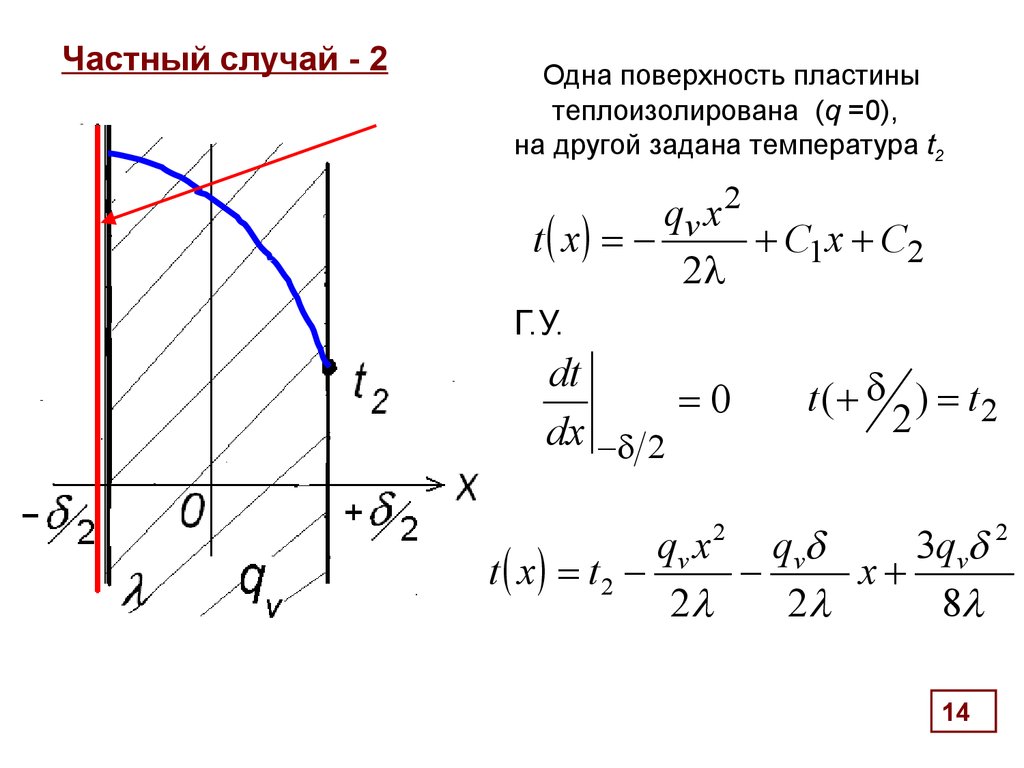
14. Частный случай - 2

Одна поверхность пластины
теплоизолирована (q =0),
на другой задана температура t2
qv x 2
t x C1x C2
2
Г.У.
dt
0
dx - 2
t ( ) t2
2
qv x
q v
3qv
t x t2 x
2
2
8
2
14
2

15. Поле температуры в цилиндрической стенке без тепловыделения

2
t 0
2
2
1 t 1 t t
t 2
2
2
2
r r r
r
z
2
t
2
2
d t
1 dt
0
dr 2 r dr
t (r1 ) t1
t (r2 ) t 2
Условия однозначности
1. геометрические - r1, r2
2. физические
-
3. начальные
4. граничные I рода
15

16. Поле температуры в цилиндрической стенке

замена переменных
du 1
u 0
dr r
dt
u
dr
du
dr
u
r
После двукратного интегрирования
t r C1 ln r C2
t1 - t 2
C1
ln r1 r2
t1 - t 2
C 2 t1 ln r1
ln r1 r2
ln r r1
t (r ) t1 - t1 - t 2
ln r2 r1
16

17. Поле температуры в цилиндрической стенке

Логарифмический закон изменения температуры по радиусу 
является следствием уменьшения плотности теплового потока 
с увеличением радиуса.
Количество тепла, проходящее через цилиндрическую поверхность  
                     в единицу времени
dt
F 2 rl
dt
Q -
2 l (t1 - t 2 )
Q
ln d 2 d1
dr
F
dr
из решения уравнения
Q (t1 - t 2 )
ql
d2
1
l
Тепловой поток, отнесенный к единице длины 
ln
трубы (линейный тепловой поток)
2 d1
17

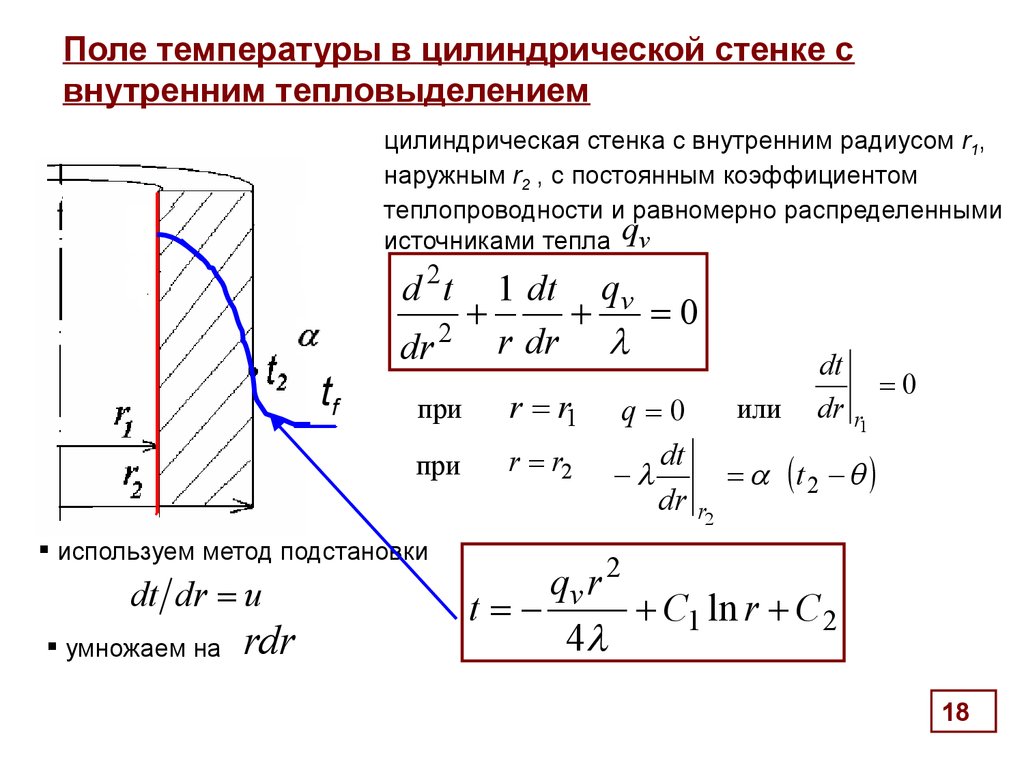
18. Поле температуры в цилиндрической стенке с внутренним тепловыделением

цилиндрическая стенка с внутренним радиусом r1,
наружным r2 , с постоянным коэффициентом
теплопроводности и равномерно распределенными
источниками тепла qv
d 2t
1 dt qv
0
2
r dr
dr
tf
при    r r1
           
при   
используем метод подстановки
dt dr u
умножаем на
rdr
r r2
q 0
dt
-
dr
r2
dt
   или      dr
0
r1
t2 -
qv r 2
t C1 ln r C 2
4
18

19. Поле температуры в цилиндрической стенке с внутренним тепловыделением

qv r C1
dt
dr
2
r
Подставляем сюда r1
qv r12
C1
2
Из второго граничного условия 
qv r2 qv r22 qv r12 qv r12
C2 t f
ln r2
2
4 2 r2
2
Распределение температуры в цилиндрической стенке  при заданных Г.У.   
2
2
qv r2
r1 qv r2
1 -
t r t f
2 r2 4
2
r 2
r
r
1
1 2 ln -
r2 r2
r2
2
r1
qv r2
Температура внешней поверхности  t 2 t f 2 1 - r
2
Плотность теплового потока на r2 
2
2
qv r2
r1
1 -
q t2 - t f
2 r2
Перепад температур в стенке
2
2
qv r2 r2
r2
- 2 ln - 1
t1 - t 2
4 r1
r1 19

20. Поле температуры в сплошном цилиндре

2
1 dt qv
0
2
r dr
dr
d t
уравнение
qv r 2
t C1 ln r C 2
4
решение
tf
С1=0
распределение
температуры в цилиндре
с внутренним
тепловыделением
Г.У.
r r0
r 0
dt
-
dr
t - t f
r0
dt
0
dr r 0
условие
симметрии
2
r
qv r0 qv r0
1 -
t r t f
2
4 r0
2
20

21. Поле температуры в сплошном цилиндре

температура внешней поверхности
цилиндра
qr
t2 t f
tf
v 0
2
перепад температур в цилиндре
2
qv r0
t t r 0 - t 2
4
плотность теплового потока на
поверхности цилиндра
qv r0
q
2
21

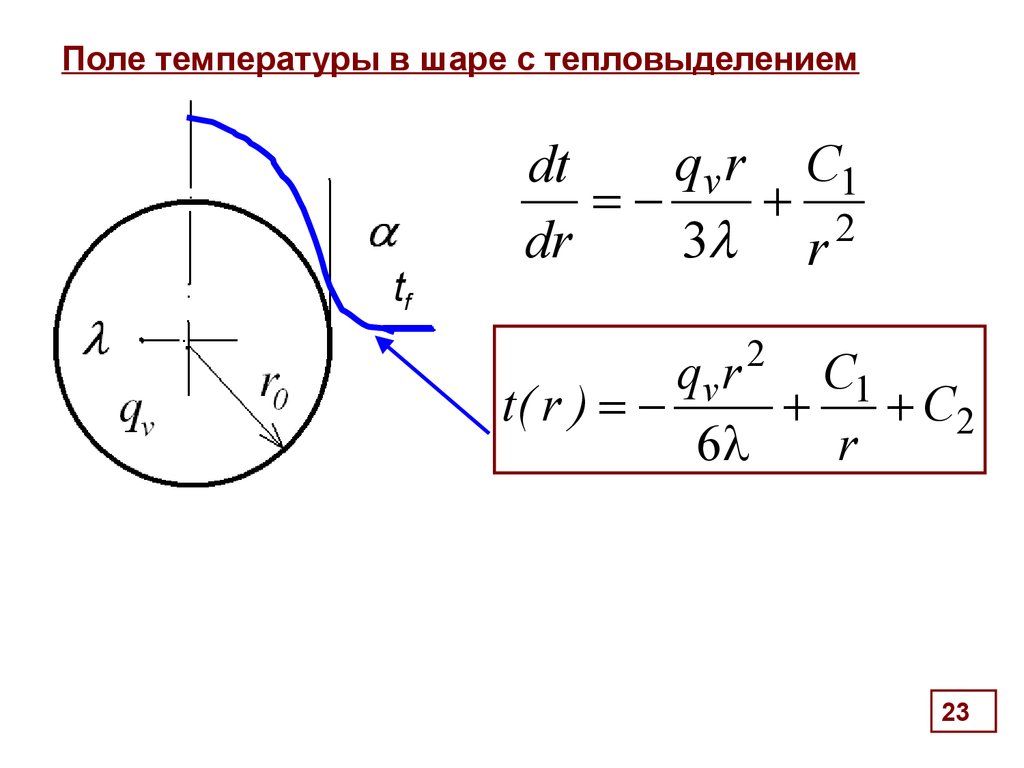
22. Поле температуры в шаре с тепловыделением

*
2 dt qv
0
2
r dr
dr
2
d t
   
tf
    
Граничные условия:   
r 0
r r0
     
подстановка
dt
0
dr
dt
- t w -
dr
u dt dr
умножение всех членов уравнения (*) на
2
r dr
22

23. Поле температуры в шаре с тепловыделением

tf
    
     
qv r C1
dt
2
dr
3 r
2
qv r
C1
t( r ) C2
6
r
23

24. Поле температуры в шаре с тепловыделением

из граничных условий      
C1 0
qv r0 1 r0
C2 t f
t r 0
3 2
Распределение температур в шаре:
2
qv r0 1 r0 qv r
t r t f
3 2 6
перепад температур в шаре
qv r02
t
6
плотность теплового потока 
на поверхности шара
dt
q -
dr
r0
qv r0
3
24

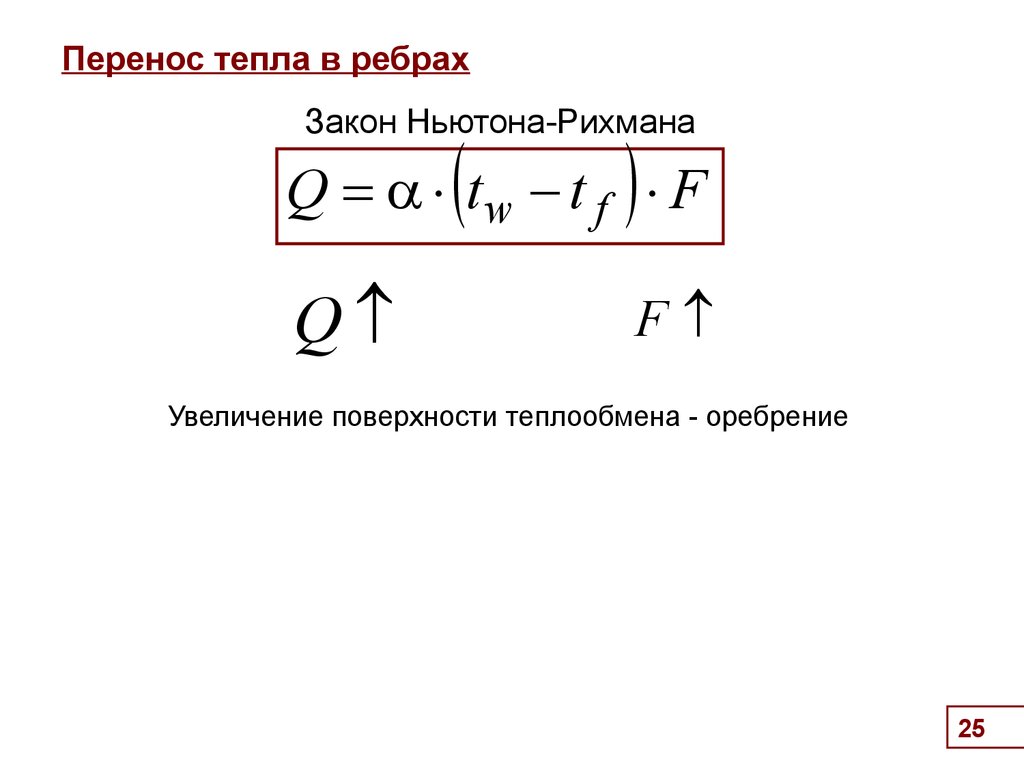
25. Перенос тепла в ребрах

Закон Ньютона-Рихмана
Q tw - t f F
Q
F
Увеличение поверхности теплообмена - оребрение
25

26. Перенос тепла в ребрах

1. Кипящая вода 1
2. Свободная конвекция в воздухе
1 2
2
полное термическое сопротивление
1 1
R
1 2
пренебрегаем
1
1 2 1
1
1
R
~
~
1 2
1 2
1 2 2
Полное термическое сопротивление имеет порядок большего 
термического сопротивления, там и делают оребрение 
26

27. Перенос тепла в ребрах

27

28. Перенос тепла в ребрах

Ребро в виде стержня (сечение F, периметр P, длина l ), 
который охлаждается конвекцией с постоянным 
коэффициентом теплообмена     , 
температура при основании стержня to
температура окружающей жидкости tf
28

29. Перенос тепла в ребрах

Через сечение х передается количество тепла
На длине dx отводится тепло конвекцией, 
изменение потока тепла
dt
Q - F
dx
dQ
d 2t
dQ
dx - 2 Fdx
dx
dx
По закону Ньютона-Рихмана
-
d 2t
dx
dQ t - t f Pdx
Fdx
t
t
Pdx
f
2
29

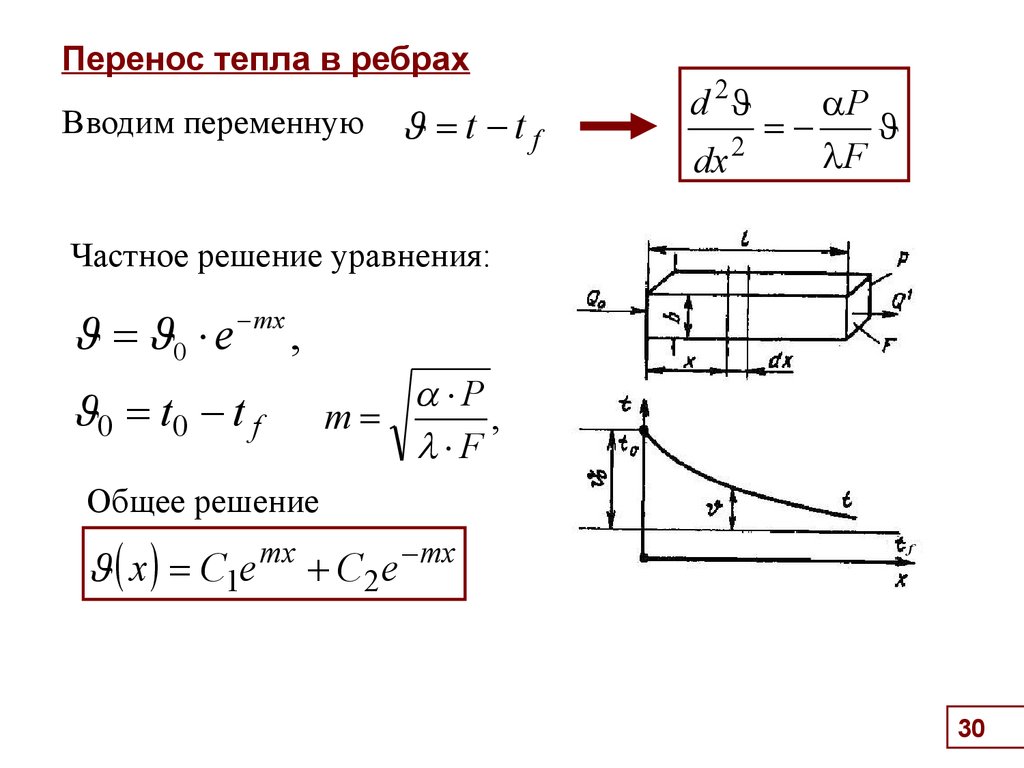
30. Перенос тепла в ребрах

Вводим переменную
t -tf
d 2
P
2
F
dx
Частное решение уравнения:
0 e
- mx
,
P
m
,
F
0 t0 - t f
Общее решение
x C1e
mx
C2 e
- mx
30

31. Перенос тепла в ребрах

     
Перенос тепла в ребрах
С1 и С2 определяются из Г.У., которые могут быть 
различными в зависимости от длины ребра и его формы.
t t0 0
при       x 0
Если 
длина 
стержня  d
0
больше  его  толщины,  то  отводом  тепла  с  торца 
dx x l
(Q') можно пренебречь                          
x 0 e
Число Био
     (Biot)      
- mx
x
mx 2 Bid
dэ
dэ
Bid
w
4F
dэ
P
эквивалентный 
диаметр
31

32. Перенос тепла в ребрах

     
Перенос тепла в ребрах
Тепловой поток через основание стержня
Q P F 0
К расчету переноса тепла вдоль стержневого ребра
32

33. Перенос тепла в ребрах

     
Перенос тепла в ребрах
Расчет переноса тепла через ребра приближенный.
Коэффициент теплообмена не является постоянной величиной,
толщина ребер может меняться, температура по сечению ребра
также не постоянна.
33

34. Перенос тепла в ребрах

     
Перенос тепла в ребрах
Коэффициент эффективности ребра  -  отношение 
теплового  потока  от  ребра  (   Q      )  к  тепловому  потоку  от 
идеального  ребра  с  бесконечно  большим  коэффициентом 
Qид                                 
теплопроводности (        ):
Q Qид
Допущение о бесконечно большой теплопроводности
приводит к выводу, что температура ребра по длине
будет постоянной
34

35. Перенос тепла в ребрах

     
Перенос тепла в ребрах
Коэффициент  эффективности  ребра  с  постоянным 
поперечным сечением и тепловой изоляцией на торце
th
BiL
BiL
L
w
L
BiL
1
w
комплекс, имеющий
P l2
L
- размерность длины
F
термическое сопротивление ребра
конвективное термическое сопротивление
Критерий Био
35

36. Перенос тепла в ребрах

     
Перенос тепла в ребрах
быстро снижается с ростом числа Bi.
Ребро с большим значением Bi рассеивает тепло хуже, чем ребро с
меньшим числом Bi
для ребер надо выбирать материал с высокой теплопроводностью
Если
мал, то поверхность без ребра будет отдавать тепло
более интенсивно, чем поверхность с ребрами.
При больших Bi кондуктивное термическое сопротивление велико
по сравнению с конвективным термическим сопротивлением, и
поэтому температура существенно падает вдоль ребра.
Если Bi велико, то площадь, занятая ребрами с малой теплопроводностью, "изолирует" поверхность отвода тепла.
Важно установить условия, когда выгодно иметь
ребристую поверхность
?
36

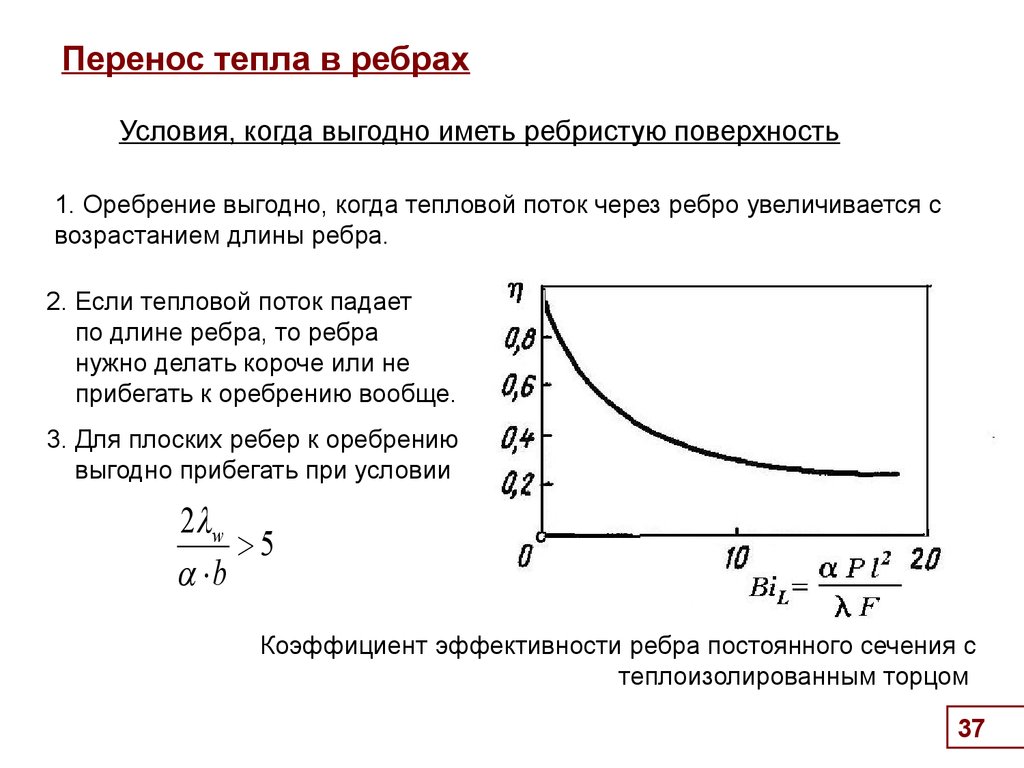
37. Перенос тепла в ребрах

     
Перенос тепла в ребрах
Условия, когда выгодно иметь ребристую поверхность
1. Оребрение выгодно, когда тепловой поток через ребро увеличивается с
возрастанием длины ребра.
2. Если тепловой поток падает
по длине ребра, то ребра
нужно делать короче или не
прибегать к оребрению вообще.
3. Для плоских ребер к оребрению
выгодно прибегать при условии
2 w
5
b
Коэффициент эффективности ребра постоянного сечения с
теплоизолированным торцом
37

38. Перенос тепла в ребрах

     
Перенос тепла в ребрах
Распределение температуры в плоском ребре
38

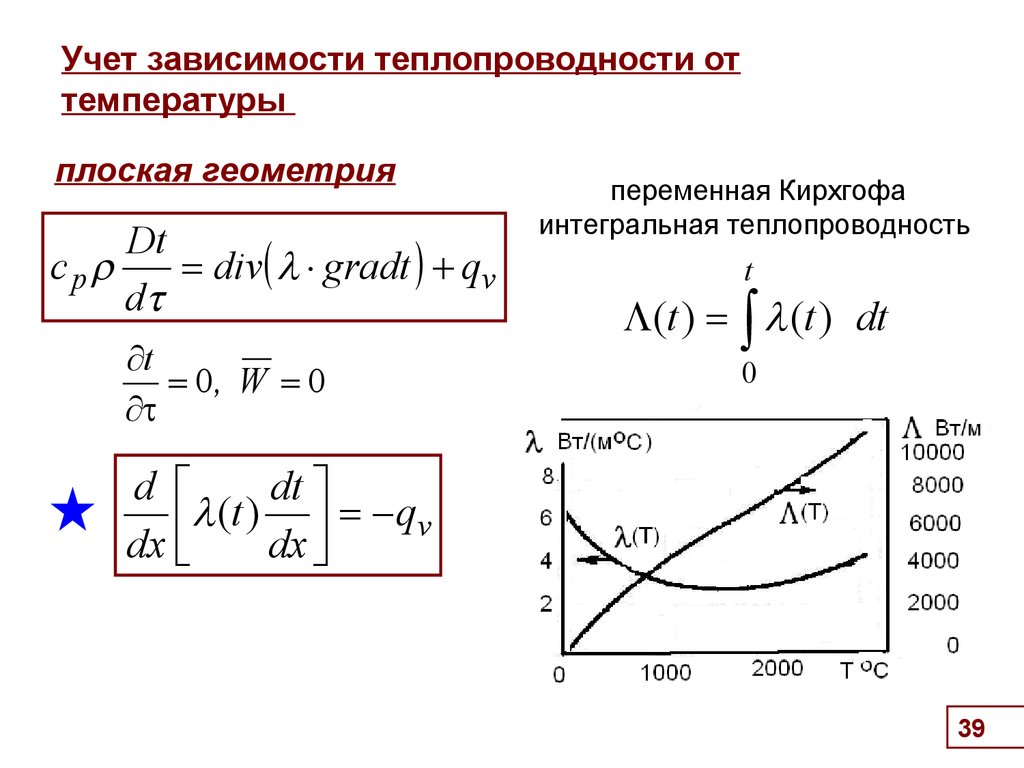
39. Учет зависимости теплопроводности от температуры

     
Учет зависимости теплопроводности от
температуры
плоская геометрия
Dt
cp
div gradt qv
d
t
0, W 0
переменная Кирхгофа
интегральная теплопроводность
t
(t ) (t ) dt
0
d
dt
(t ) -qv
dx
dx
39

40. Учет зависимости теплопроводности от температуры

     
Учет зависимости теплопроводности от
температуры
Т.к. производная от интеграла по верхнему пределу 
есть подинтегральная функция, т.е. 
d
d d dt
dt
(t )
dx
dt dx
dx
2
d
dx
2
dt
(t )
-qv
(t )
решаем относительно          , затем находим температуру
40

41. Учет зависимости теплопроводности от температуры (цилиндрическая геометрия)

     
Учет зависимости теплопроводности от
температуры (цилиндрическая геометрия)
уравнение теплопроводности для сплошного цилиндра 
r
                                                              (таблетка топлива радиусом R) 
dt
                                                              с переменным  
qv ( r ) 2 r dr - ( t ) 2 r
qv r
dr
                                                              тепловыделением
                    :
0
После интегрирования 
обеих частей уравнения  
                                          
в пределах от 0 до r :
Интегрирование в пределах 
от r до R :
r
dr
r
0
R
dr
r
r
r
t( r )
0
t( 0 )
qv ( r ) r dr - ( t )dt
r
t( r )
R
t( R )
qv ( r ) r dr ( t )dt
t( r )
Для постоянного 
тепловыделения:
qv ( R 2 - r 2 )
. ( t )dt
4
t( R )
41

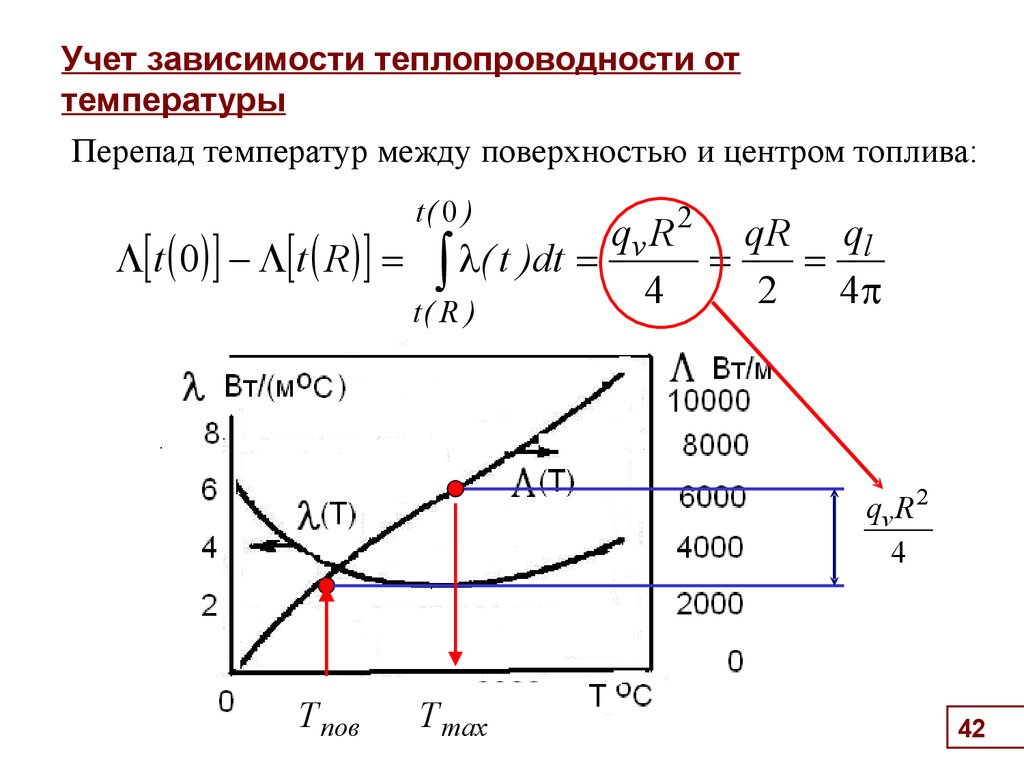
42. Учет зависимости теплопроводности от температуры

     
Учет зависимости теплопроводности от
температуры
Перепад температур между поверхностью и центром топлива:
t( 0 )
qv R 2 qR ql
t 0 - t R ( t )dt
4
2
4
t( R )
.
qv R 2
4
Т пов
Т max
42

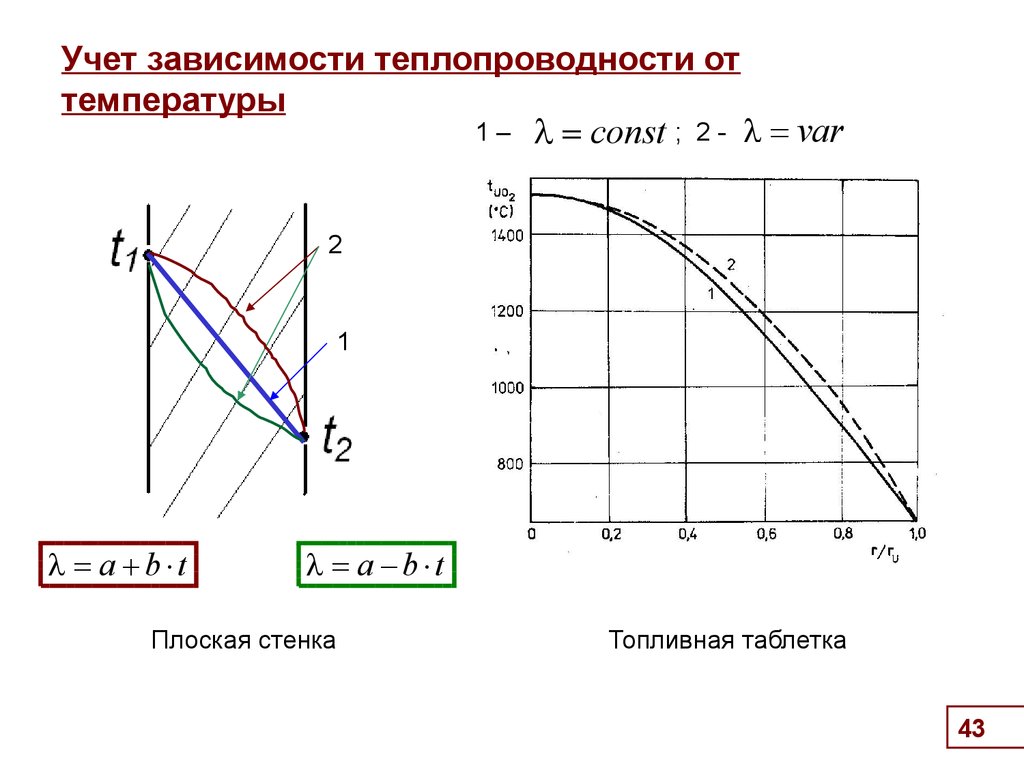
43. Учет зависимости теплопроводности от температуры

     
Учет зависимости теплопроводности от
температуры
1–
const ;
2-
var
2
1
a b t
a - b t
Плоская стенка
Топливная таблетка
43

44. Обмуровка трубопроводов

Хромитовая масса
Жароупорный бетон
Теплоизоляционный бетон
Газоплотная обмазка и штукатурка

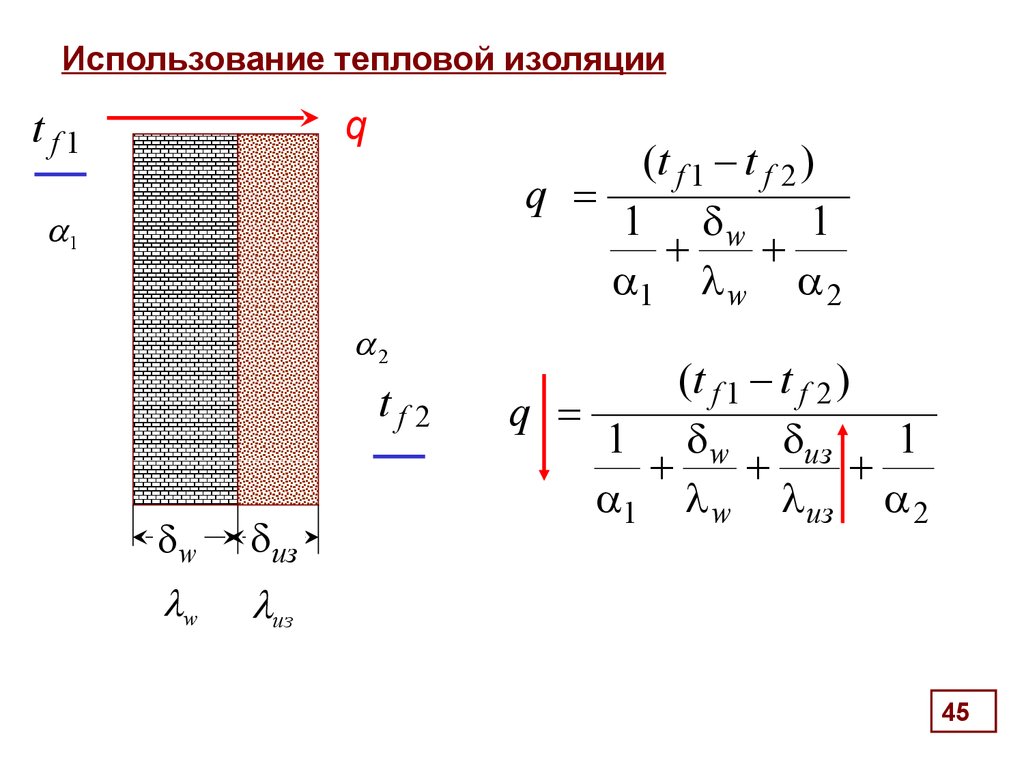
45. Использование тепловой изоляции

q
tf1
(t f 1 - t f 2 )
q
1 w 1
1 w 2
1
2
tf 2
w
из
w
из
(t f 1 - t f 2 )
q
1 w из
1
1 w из 2
45

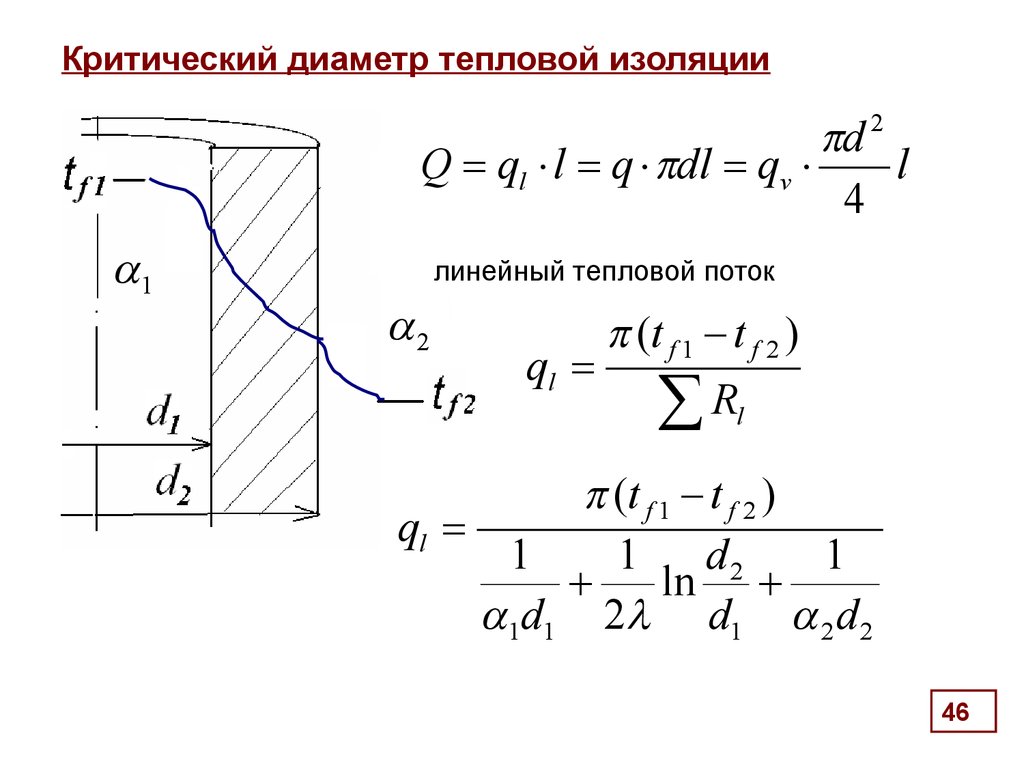
46. Критический диаметр тепловой изоляции

d 2
Q ql l q dl qv
l
4
1
линейный тепловой поток
2
(t f 1 - t f 2 )
ql
Rl
(t f 1 - t f 2 )
ql
1
1
d2
1
ln
1d1 2 d1 2 d 2
46

47. Критический диаметр тепловой изоляции

1
w
2
(t f 1 - t f 2 )
ql
d3
1
1
d2
1
1
ln
ln
1d1 2 w d1 2 из d 2 2 d 3
Rl1
Rl2
Rl3
Rl4
из
R Rl1 Rl 2 Rl 3 Rl 4
47

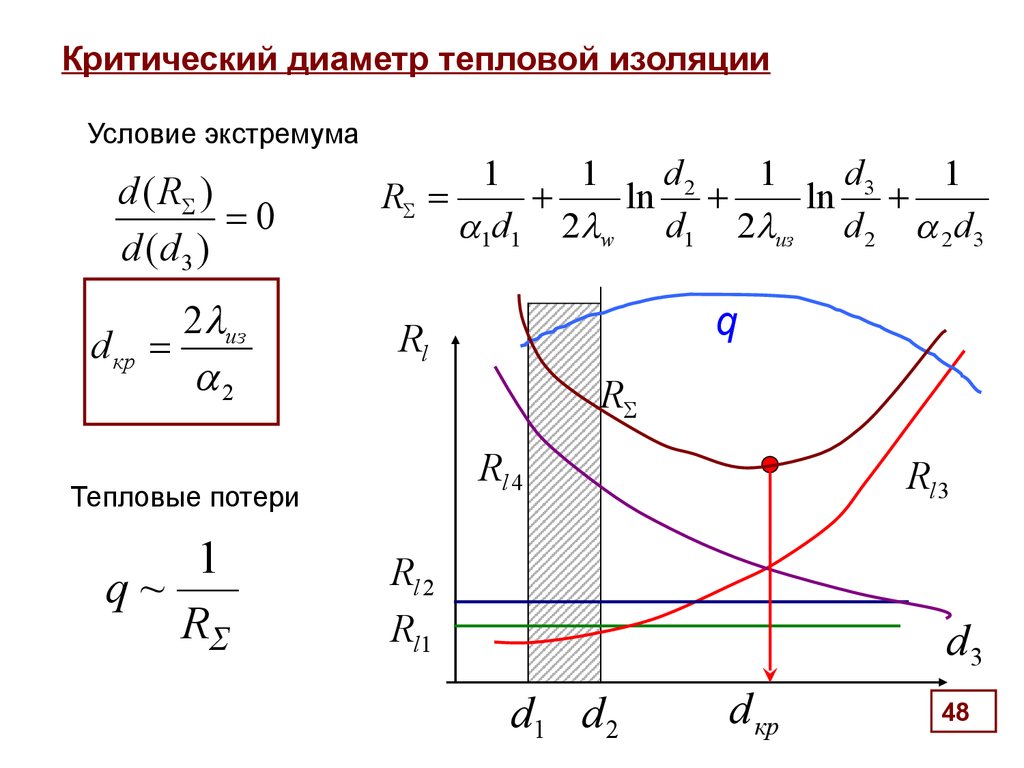
48. Критический диаметр тепловой изоляции

Условие экстремума
d ( R )
0
d (d 3 )
2 из
d кр
2
d3
1
1
d2
1
1
R
ln
ln
1d1 2 w d1 2 из d 2 2 d 3
R
Rl 4
Тепловые потери
1
q~
R
q
Rl
Rl 3
Rl 2
Rl1
d3
d1 d 2
d кр
48

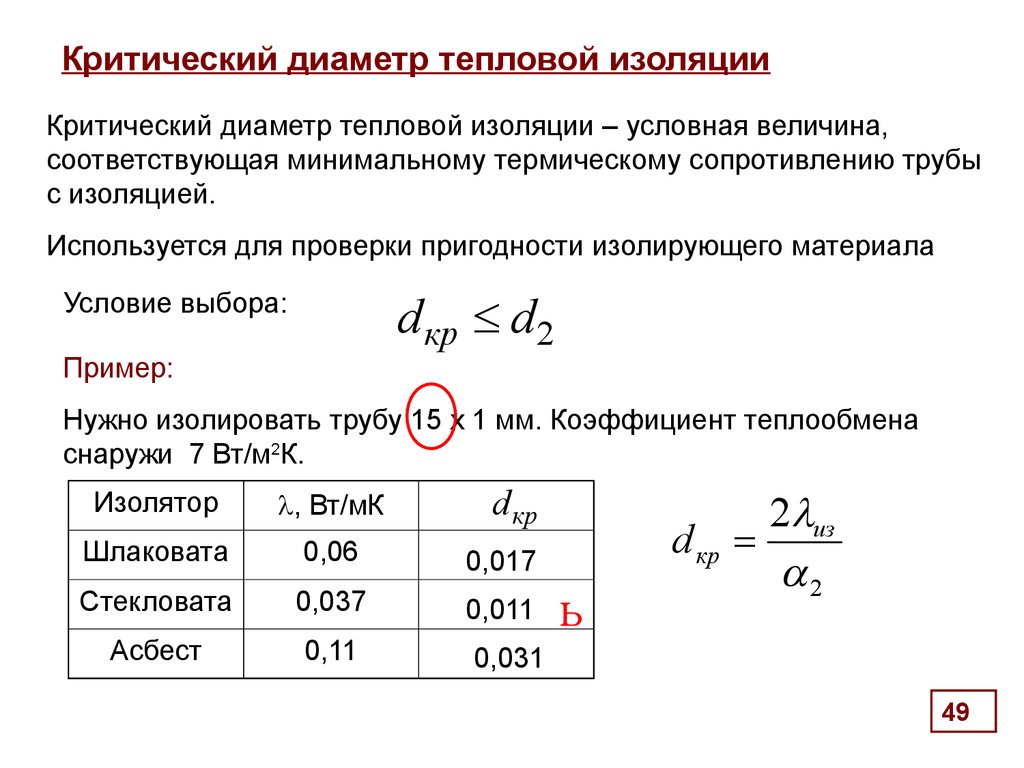
49. Критический диаметр тепловой изоляции

Критический диаметр тепловой изоляции – условная величина,
соответствующая минимальному термическому сопротивлению трубы
с изоляцией.
Используется для проверки пригодности изолирующего материала
d кр d 2
Условие выбора:
Пример:
Нужно изолировать трубу 15 х 1 мм. Коэффициент теплообмена
снаружи 7 Вт/м2К.
d кр
Изолятор
, Вт/мК
Шлаковата
0,06
0,017
Стекловата
0,037
0,011
Асбест
0,11
ь
2 из
d кр
2
0,031
49