Похожие презентации:
Электротехника и электроника. Гармонические колебания в пассивных элементах электрических цепей. (Лекция 5)
1.
Кубанский государственный технологический университетИнститут информационных технологий и безопасности
Кафедра компьютерных технологий и информационной
безопасности
Учебная дисциплина
Электротехника и электроника
Лекция № 5
Гармонические колебания в
пассивных элементах
электрических цепей
2.
Учебные вопросы:1. Гармонические колебания в пассивных элементах
электрических цепей.
2. Мощность электрической цепи
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 61 –84.
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 37 –54.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для
вузов, - М.: Высшая школа, 2003 г, с. 37 –83.
3.
1. Гармонические колебания в пассивных элементах электрической цепи.i(t)
1.1 Резистивный элемент и его характеристики
R
Пусть через резистор протекает ток i(t):
i (t ) I m sin( t i ) I m e
uR(t)
j ( t i )
I m e j t
u (t ) R i (t ) R I m sin( t i ) U mR sin( t i ) U mR sin( t u )
u (t ) R I m e
j t
U mR e
j t
j i
U mR e e
j t
U mR e
j u
e
j t
комплексная
форма
записи
Мгновенная мощность колебания в резисторе
j
R 0
Im
p (t ) u i RI m sin( t i ) I m sin( t i )
Um
RI sin ( t i ) U mR I m sin ( t i )
2
m
2
2
2U mR I m 2
sin ( t i ) 2U R I sin 2 ( t i )
2 2
+1
Колебания синфазные U I 1 cos 2( t ) 0
R
i
u= i
U mR R I m U R I
R
4.
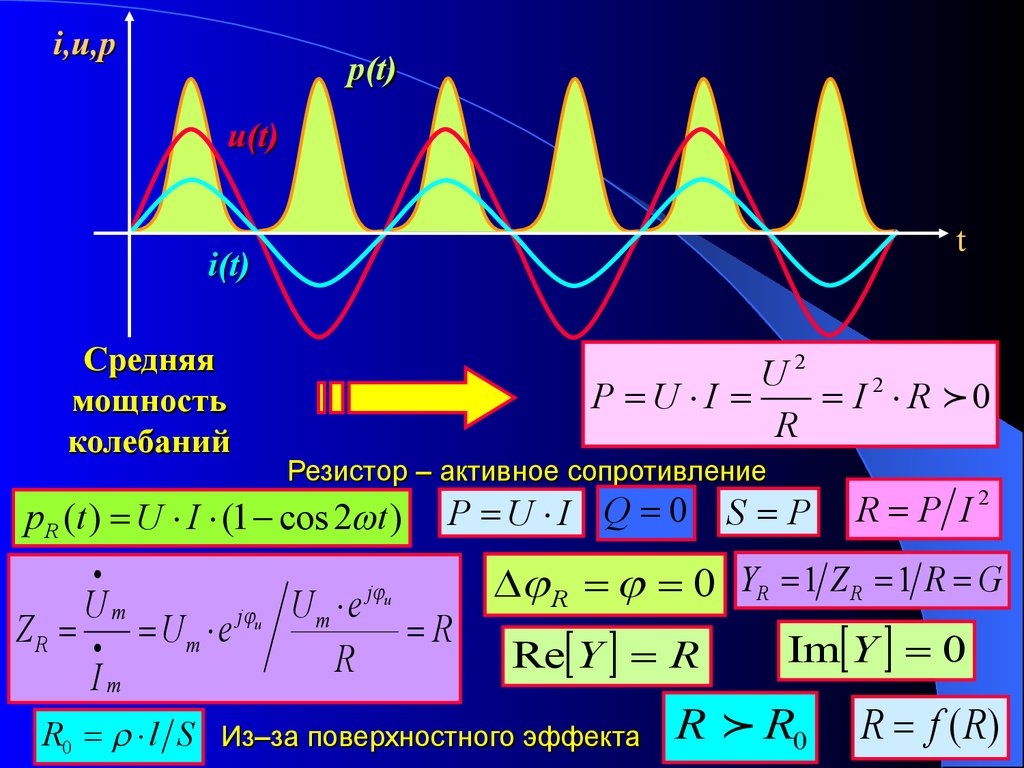
i,u,pp(t)
u(t)
t
i(t)
Средняя
мощность
колебаний
U2
P U I
I 2 R 0
R
Резистор – активное сопротивление
pR (t ) U I (1 cos 2 t )
ZR
Um
Im
Um e
j u
Um e
R
j u
P U I Q 0
R
S P
R P I2
R 0 YR 1 Z R 1 R G
Re Y R
R0 l S Из–за поверхностного эффекта
Im Y 0
R R0
R f (R)
5.
1.2 Индуктивный элемент и его характеристикиL
i
d ( I m sin( t i ))
di
uL L L
L I m cos( t i )
dt
dt
uL(t)
U mL cos( t i ) U mL sin( t i ) U mL sin( t u )
i (t ) I m sin( t i )
2
u i ; u i
2
2
ZL
U mL
Im
j ( i 90 )
L Im e
I m e j i
U mL L I m
L e
j 90
j L
X L ( ) L
Комплексное
сопротивление
L -элемента
Z L ( j ) j L j X L Re Z L 0 Im Z L L X L
Комплексная проводимость L -элемента
1
1
YL
j
L
Z L j L
1
1
bL
Re YL 0 Im YL
L
6.
Напряжение на индуктивностиимеет форму гармонического
колебания и опережает по фазе
колебания тока на угол + /2.
Колебания тока и напряжения
находятся в квадратуре
j
Um
u
Im
i
+1
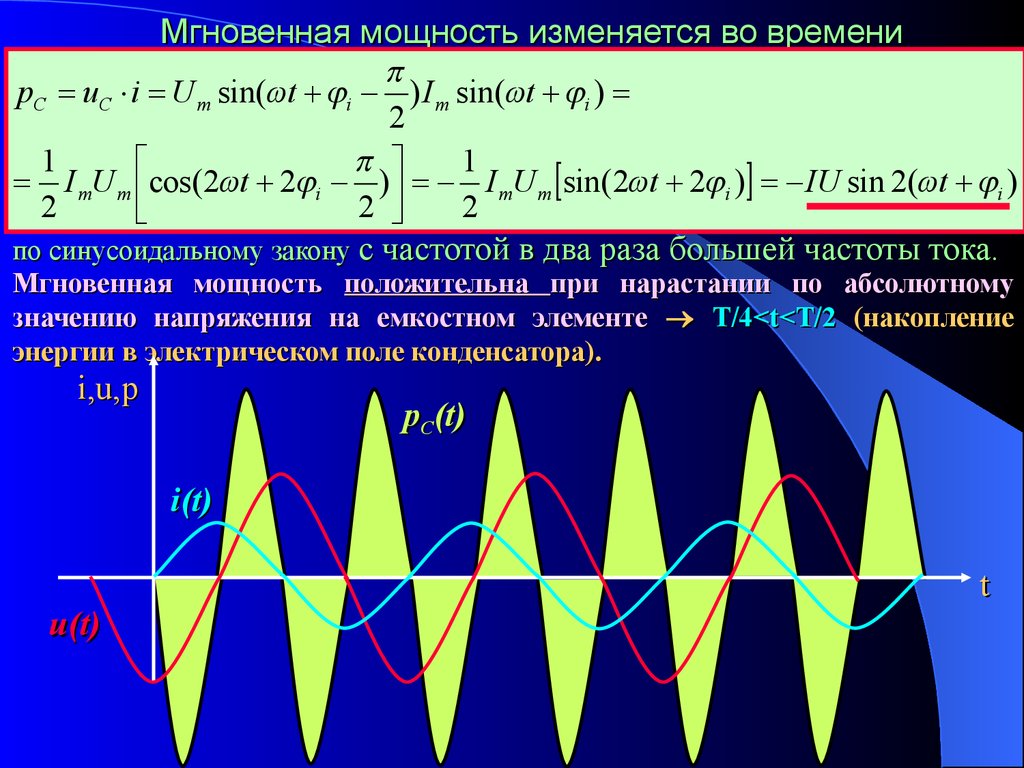
Мгновенная мощность изменяется во времени
pL u L i U m sin( t i ) I m sin( t i )
2
1
1
I mU m cos( t i t i ) I mU m cos( t i t i )
2
2 2
2
1
1
I mU m cos(2 t 2 i ) I mU m sin( 2 t 2 i ) IU sin 2( t i )
2
2 2
по синусоидальному закону с частотой в два раза большей частоты тока
Мгновенная мощность положительна при нарастании по абсолютному
значению тока в индуктивном элементе 0<t<Т/4 (накопление энергии в
магнитном поле катушки индуктивности).
7.
Энергия поступающая в индуктивный элемент за четверть периода (р >0)T /4
WL
p
0
L
T /4
T /4
0
0
(t )dt u L idt
i,u,p
T /4
LI m2
di
L idt L i di
dt
2
0
PL 0
pL(t)
QL I 2 X L
u(t)
S L QL
t
i(t)
Средняя за
период мощность
в индуктивном
элементе
T
T
1
1 1
P pL (t )dt I mU m sin( 2 t 2 i ) dt 0
T0
T 02
8.
1.3 Емкостной элемент и его характеристикиС
1
1
i(t
uС idt I m sin( t i )dt
C
C
)
Im
Im
uС(t)
cos( t i )
sin( t i )
C
C
2
i (t ) I m sin( t i )
U mC sin( t i ) U mC sin( t u )
2
Im
u i ; u i
U mС
X C ( ) I m
2
2
C
Напряжение на емкостном
элементе
имеет
форму
гармонического колебания
и отстает по фазе
от
колебания тока на угол /2.
1
1
Z C ( j )
j
jX C
j C
C
j
Im
i
u
Re Z C 0
Um
+1
YC ( ) j C
Im Z C 1
C XC
9.
Мгновенная мощность изменяется во времениpС uС i U m sin( t i ) I m sin( t i )
2
1
1
I mU m cos(2 t 2 i ) I mU m sin( 2 t 2 i ) IU sin 2( t i )
2
2
2
по синусоидальному закону с частотой в два раза большей частоты тока.
Мгновенная мощность положительна при нарастании по абсолютному
значению напряжения на емкостном элементе Т/4<t<Т/2 (накопление
энергии в электрическом поле конденсатора).
i,u,p
pС(t)
i(t)
t
u(t)
10.
Энергия поступающая в емкостной элемент за четверть периода(рС > 0)
T /2
WС
p
Т
L
T /2
T /2
Т
Т
(t )dt uС idt
4
4
4
Um
CU m2
du
СU m
dt C U m du
dt
2
0
T
T
Средняя за период
1
1
1
P pС (t )dt I mU m sin(2 t 2 i ) dt 0
мощность в
T0
T0 2
емкостном элементе
В чисто емкостной цепи, как и в чисто индуктивной цепи
потери энергии отсутствуют. Вначале происходит заряд
конденсатора, энергия при этом накапливается в
электрическом поле конденсатора. Затем происходит
разряд конденсатора, энергия, запасенная в электрическом
поле, поступает к источнику.
PC 0
QC U I I 2 X C
S L QC
11.
Зависимость сопротивлений пассивных элементовэлектрической цепи от частоты переменного тока
i(t)
R
L
i
R
uR(t)
uL(t)
XL
при L1
R2 > R1
при R2
X L L X L ( )
L1 > L2
при L2
при R1
ω
i(t
)
С
ω
XC
uС(t)
1
XC
X C ( )
C
C1 > C 2
при C2
при C1
ω
12.
2. Мощность электрической цепи.u (t ) U m sin( t u )
i(t)
e(t)
u(t)
i (t ) I m sin( t i )
Активная мощность
Электрическая
цепь
1
P PСР
Т
(двухполюсник)
Т
p(t ) U I cos
0
U 2 G I 2 R 0 Вт
Комплексносопряженный ток
S U I S e
j S
S e j I 2 Z
S S e j UI cos jUI sin P jQ P 2 Q 2 e j В А
[Полная мощность]=[Активная мощность]+[Реактивная мощность]
Полная мощность определяет эксплуатационные возможности
многих
электротехнических
устройств
(генераторов,
трансформаторов, электрических машин) для которых она
указывается в качестве номинальной:
номинальной SНОМ=UНОМIНОМ
13.
Реактивная мощность может быть как положительной, так и отрицательнойЕсли электрическая цепь имеет индуктивный характер, > 0 и
PQ > 0, если – емкостной характер, то < 0 и PQ < 0.
S P jQ
P
S
2
2
U
I
P Q
Q P U I cos
Р
Коэффициент мощности
Q U I sin
Чем больше cos , тем больше степень использования
P
полной мощности, тем меньшим током при заданном I
U cos
напряжении можно доставить к потребителю активную
мощность
P
cos
S
P
От значения I сечения подводящих энергию проводов, кабелей, линий
передач. Потери энергии в подводящих проводах пропорциональны I2
PПОТ I 2 RПОТ
(ток ) ( cos )
Для увеличения cos необходимо уменьшать реактивную мощность.
При Q = 0 имеем cos = 1. Так как QL > 0 , а QС < 0, то для компенсации
реактивной мощности параллельно нагрузке, имеющей как правило,
индуктивный характер, подключают компенсирующую емкость, значение
которой выбирают из условия: Q = QL + QС = 0, т.е. QL = - QС
14.
Баланс мощности в электрической цепиm
p
m
m
k 1
k 1
S ИСТ S ПРМ E k I k U 0 J 0 I 2 k Rk j I k2 X k
k 1
n 1
В электрической цепи при гармонических воздействиях выполняется баланс
комплексных мощностей источников и приемников электрической энергии
Условия получения максимальной мощности в нагрузке
I
EИ
UН ZН
Приемник
(нагрузка)
Источник
энергии
EИ
ZИ
Z И RИ jХ И Z H RH jХ H
I
ZИ ZН
EИ
( RИ RН ) j ( Х И Х Н )
2
E
2
И
P I RН
max?
2
2
( RИ RН ) ( Х И Х Н )
ХИ ХН 0
15.
Найдем экстремум функции Р2
dP
(
R
R
)
RН 2( RИ RН )
2
И
Н
E
0
4
dRН
( RИ RН )
при этом
ток в цепи
Е 2 RН
Р
( RИ RН ) 2
Экстремум
RИ RН
2
EИ I КЗ а мощность
EИ
I I0
P
P
Н
H
max
в нагрузке
2 RИ
2
4 RИ
1,0
PН MAX
0,5
PИ
PН
I0=iКЗ/2
Коэффициент полезного действия
PН ЕИ I I 2 RИ
IRИ
IRН
1
1
РИ
ЕИ I
EИ
EИ
I 2 RН
RН
2
100%
100%
2
I RИ I RН
RИ RН
I
I0=iКЗ
РMAX возможна только при = 50%
16.
Общие выводы1. В режиме холостого хода, т.е. при
RH = ∞ (разомкнутая электрическая
цепь)
2. В режиме короткого замыкания,
т.е. при RH = 0 (короткозамкнутая
электрическая цепь)
3. В согласованном режиме работы
RИ = RH
XX
RH
1
RИ RH
КЗ
RH
0
RИ RH
CP 0,5
В случае, когда необходимо обеспечить
максимальную мощность независимо от экономических
затрат (значения КПД) источники работают в
согласованном режиме (устройства автоматики –
мощности управляющих сигналов малы)
Для силовых установок (RH >> RИ) режим близкий к
режиму холостого хода важен КПД
17.
Задание насамостоятельную работу
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 61 –84.
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 37 –54.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.:
Высшая школа, 2003 г, с. 37 –83.















 Физика
Физика Электроника
Электроника








