Множественная регрессия. Типы статистических задач. (Лекция 9)

1. Регрессия – специальные варианты: нелинейная, множественная, пробит

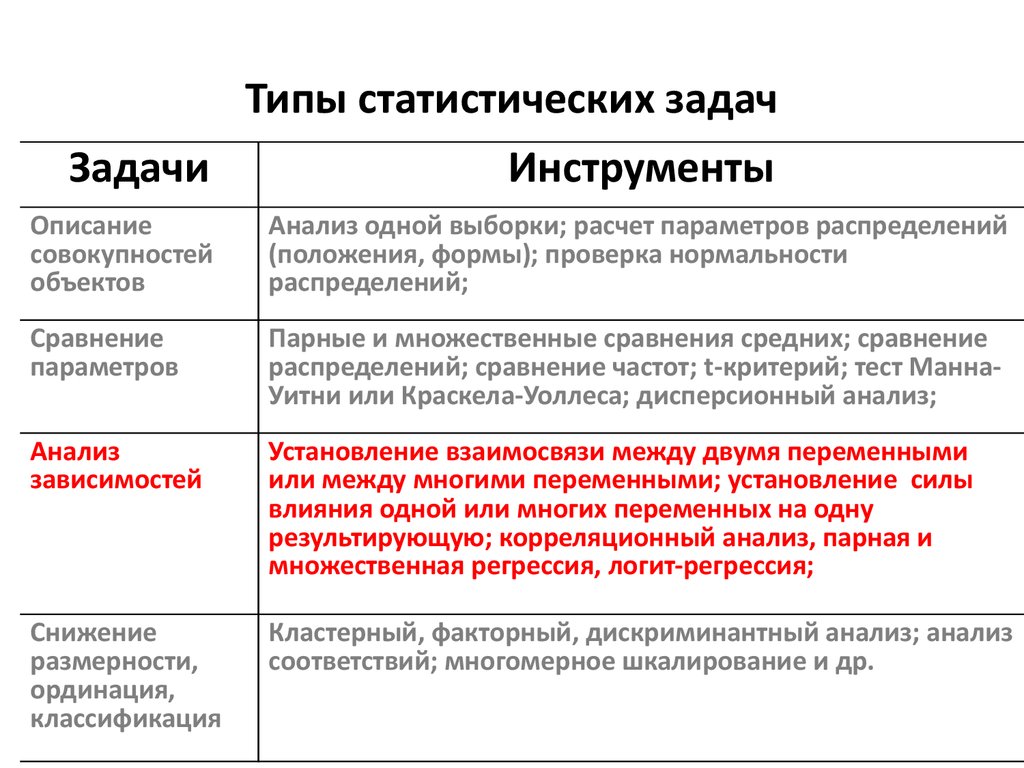
2. Типы статистических задач

Задачи
Инструменты
Описание
совокупностей
объектов
Анализ одной выборки; расчет параметров распределений
(положения, формы); проверка нормальности
распределений;
Сравнение
параметров
Парные и множественные сравнения средних; сравнение
распределений; сравнение частот; t-критерий; тест МаннаУитни или Краскела-Уоллеса; дисперсионный анализ;
Анализ
зависимостей
Установление взаимосвязи между двумя переменными
или между многими переменными; установление силы
влияния одной или многих переменных на одну
результирующую; корреляционный анализ, парная и
множественная регрессия, логит-регрессия;
Снижение
размерности,
ординация,
классификация
Кластерный, факторный, дискриминантный анализ; анализ
соответствий; многомерное шкалирование и др.

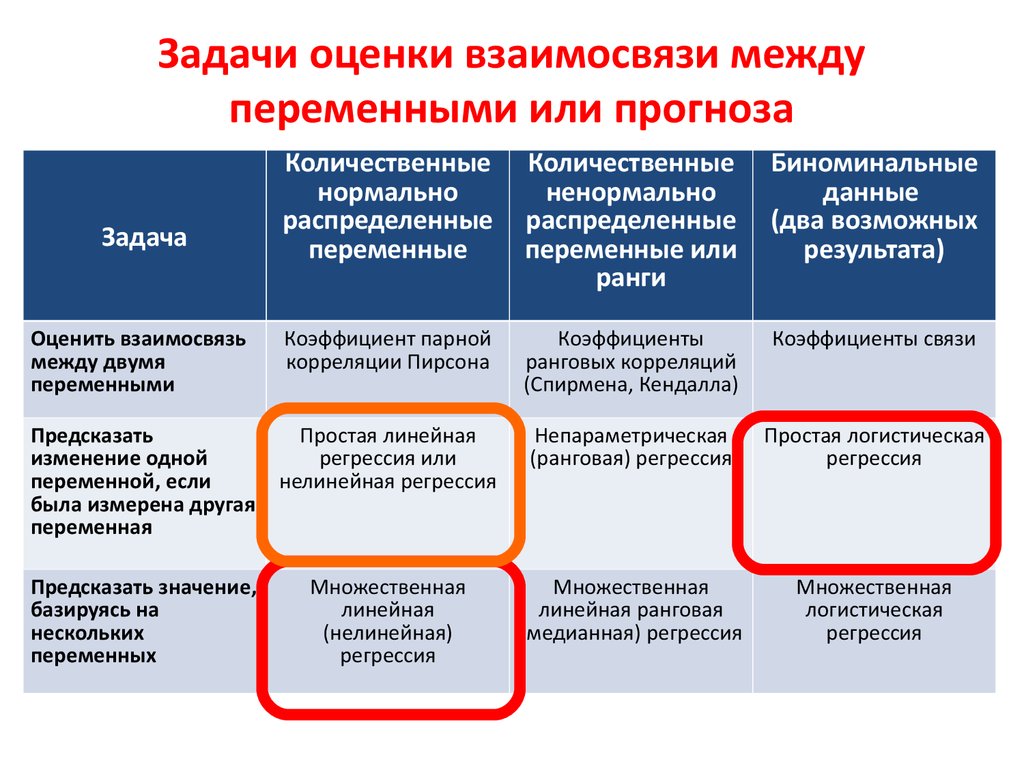
3. Задачи оценки взаимосвязи между переменными или прогноза

Количественные
нормально
распределенные
переменные
Количественные
ненормально
распределенные
переменные или
ранги
Биноминальные
данные
(два возможных
результата)
Оценить взаимосвязь
между двумя
переменными
Коэффициент парной
корреляции Пирсона
Коэффициенты
ранговых корреляций
(Спирмена, Кендалла)
Коэффициенты связи
Предсказать
изменение одной
переменной, если
была измерена другая
переменная
Простая линейная
регрессия или
нелинейная регрессия
Непараметрическая
(ранговая) регрессия
Простая логистическая
регрессия
Предсказать значение,
базируясь на
нескольких
переменных
Множественная
линейная
(нелинейная)
регрессия
Множественная
линейная ранговая
(медианная) регрессия
Множественная
логистическая
регрессия
Задача

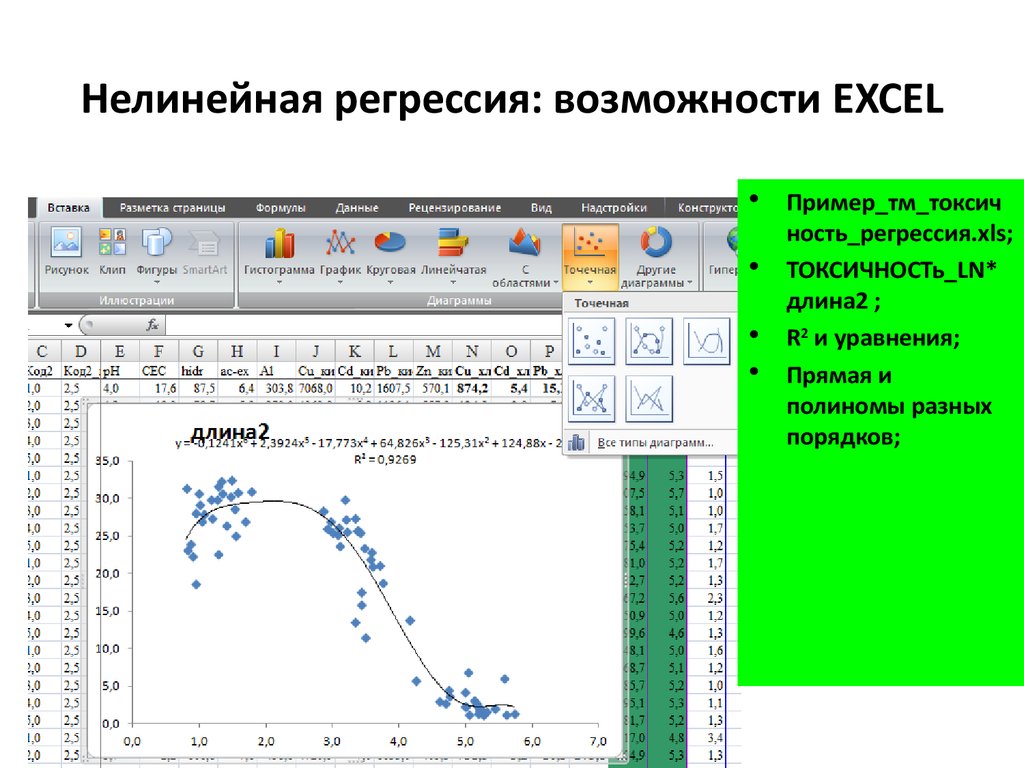
4. Нелинейная регрессия: возможности EXCEL

Пример_тм_токсич
ность_регрессия.xls;
ТОКСИЧНОСТь_LN*
длина2 ;
R2 и уравнения;
Прямая и
полиномы разных
порядков;

5. Нелинейная регрессия: эмпирические ограничения

• С ростом сложности описания ПОЧТИ ВСЕГДА растет R2;
• Необходимо найти компромисс между сложностью /
качеством и СМЫСЛОМ описания;
• Эмпирическое правило: на каждый новый член в
уравнении аппроксимирующей функции необходимо
минимум 5 – 10 независимых наблюдений;
Пример_тм_токсичность_регрессия.xls;
ТОКСИЧНОСТь_LN* длина2; ПОСТРОЕНИЯ ПО ЗОНАМ!!!
R2 и уравнения;
Прямая и полиномы разных порядков;

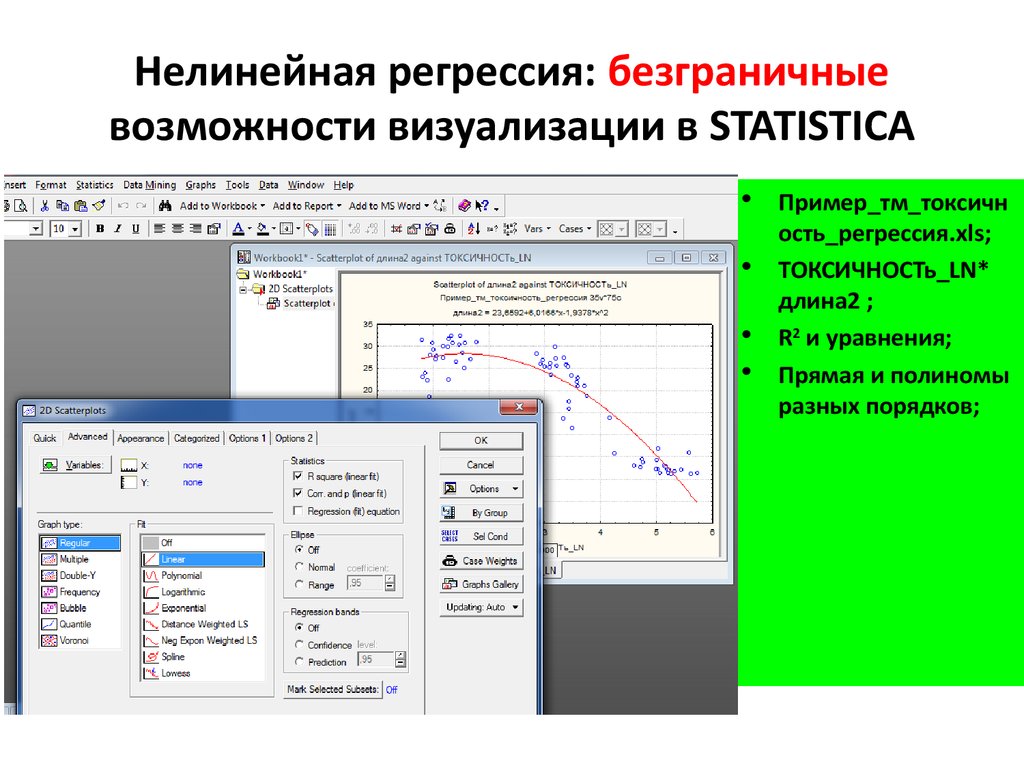
6. Нелинейная регрессия: безграничные возможности визуализации в STATISTICA

Пример_тм_токсичн
ость_регрессия.xls;
ТОКСИЧНОСТь_LN*
длина2 ;
R2 и уравнения;
Прямая и полиномы
разных порядков;

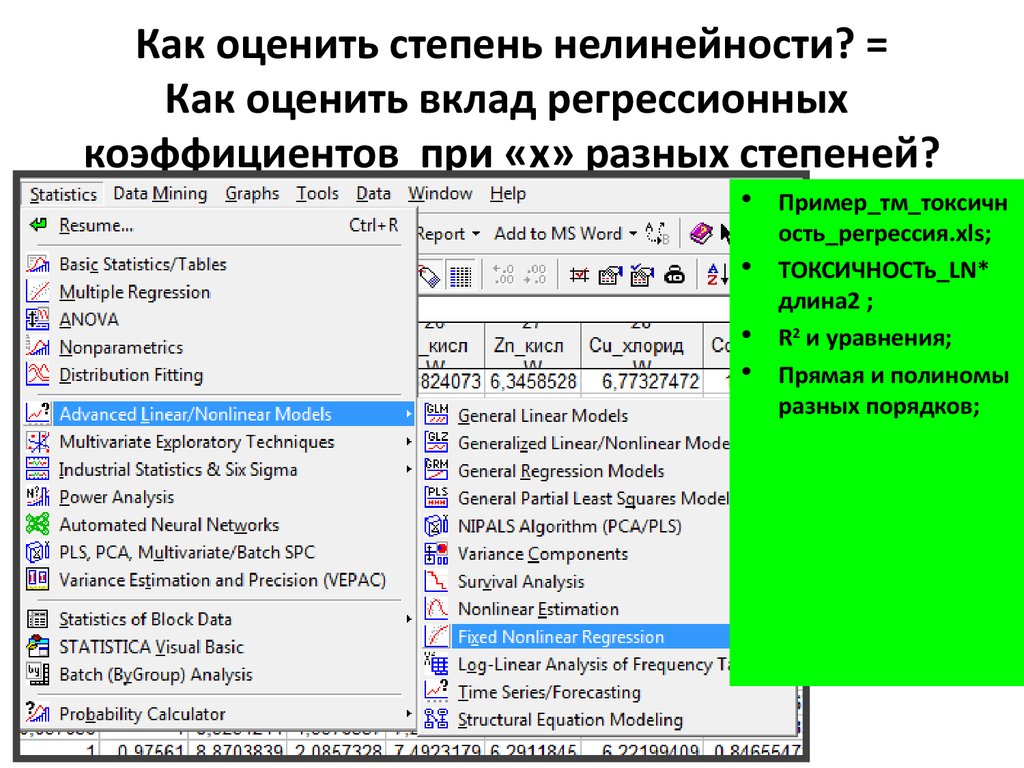
7. Как оценить степень нелинейности? = Как оценить вклад регрессионных коэффициентов при «x» разных степеней?

Пример_тм_токсичн
ость_регрессия.xls;
ТОКСИЧНОСТь_LN*
длина2 ;
R2 и уравнения;
Прямая и полиномы
разных порядков;

8. Как оценить степень нелинейности? = Как оценить вклад регрессионных коэффициентов при «x» разных степеней?

• Создаем иллюстрацию в EXCEL по
итогам определения
оптимального полинома в
STATISTICA (ТОКСИЧНОСТь_LN*
длина2);
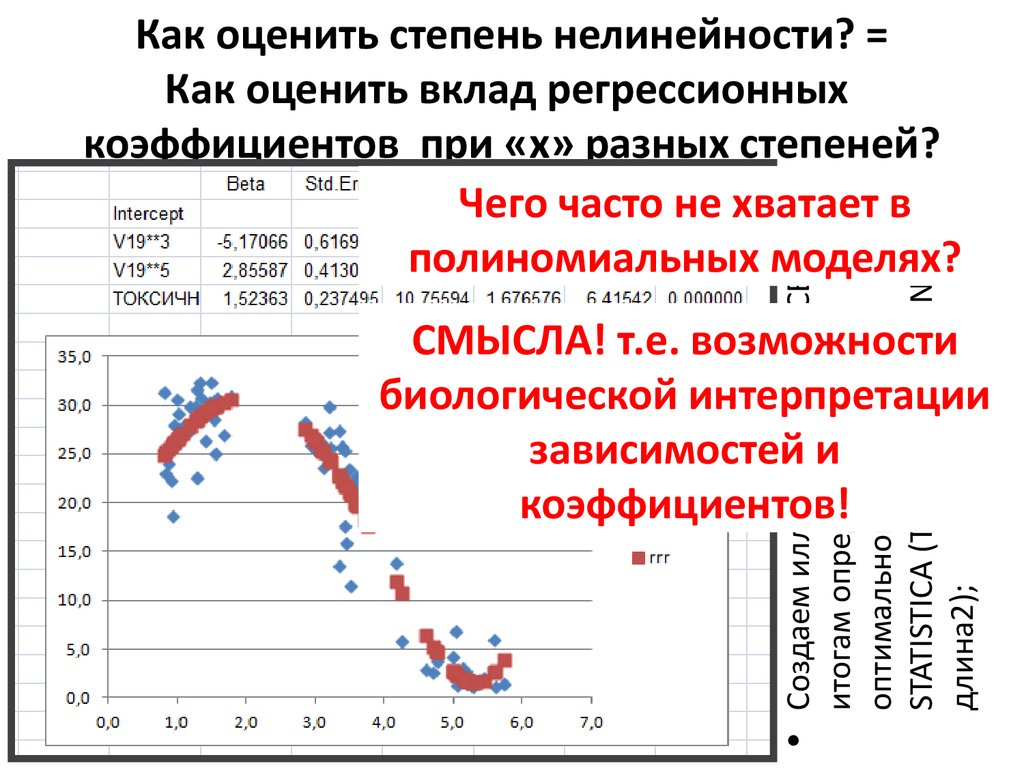
Как оценить степень нелинейности? =
Как оценить вклад регрессионных
коэффициентов при «x» разных степеней?
Чего часто не хватает в
полиномиальных моделях?
СМЫСЛА! т.е. возможности
биологической интерпретации
зависимостей и
коэффициентов!

9. Задание функции

10. Использование S-образных функций – возможность строгого аналитического нахождения граничных (критичных или желательных) оценок состояни

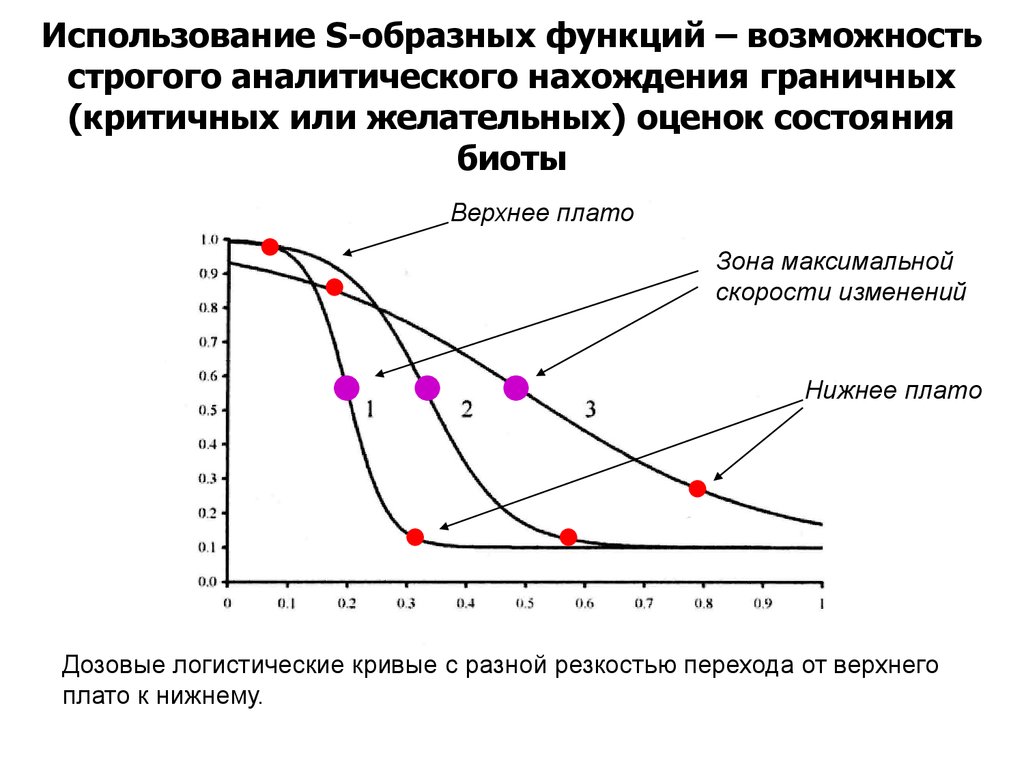
Использование S-образных функций – возможность
строгого аналитического нахождения граничных
(критичных или желательных) оценок состояния
биоты
Верхнее плато
Зона максимальной
скорости изменений
Нижнее плато
Дозовые логистические кривые с разной резкостью перехода от верхнего
плато к нижнему.

11. Нахождение координат критических точек

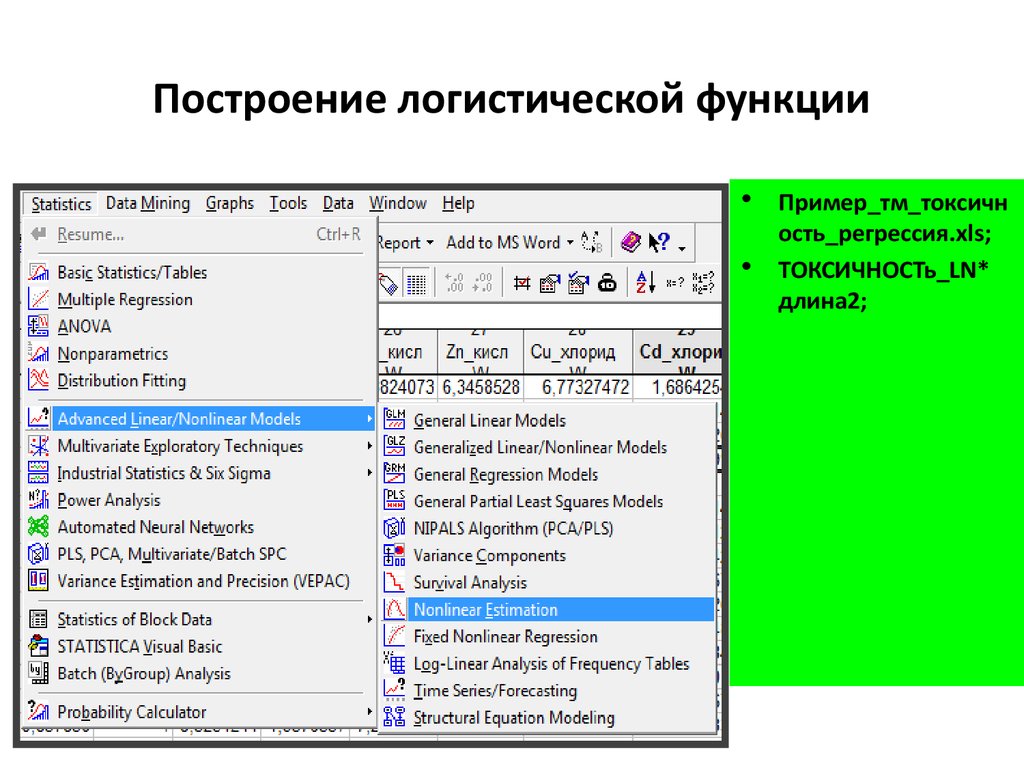
12. Построение логистической функции

Пример_тм_токсичн
ость_регрессия.xls;
ТОКСИЧНОСТь_LN*
длина2;

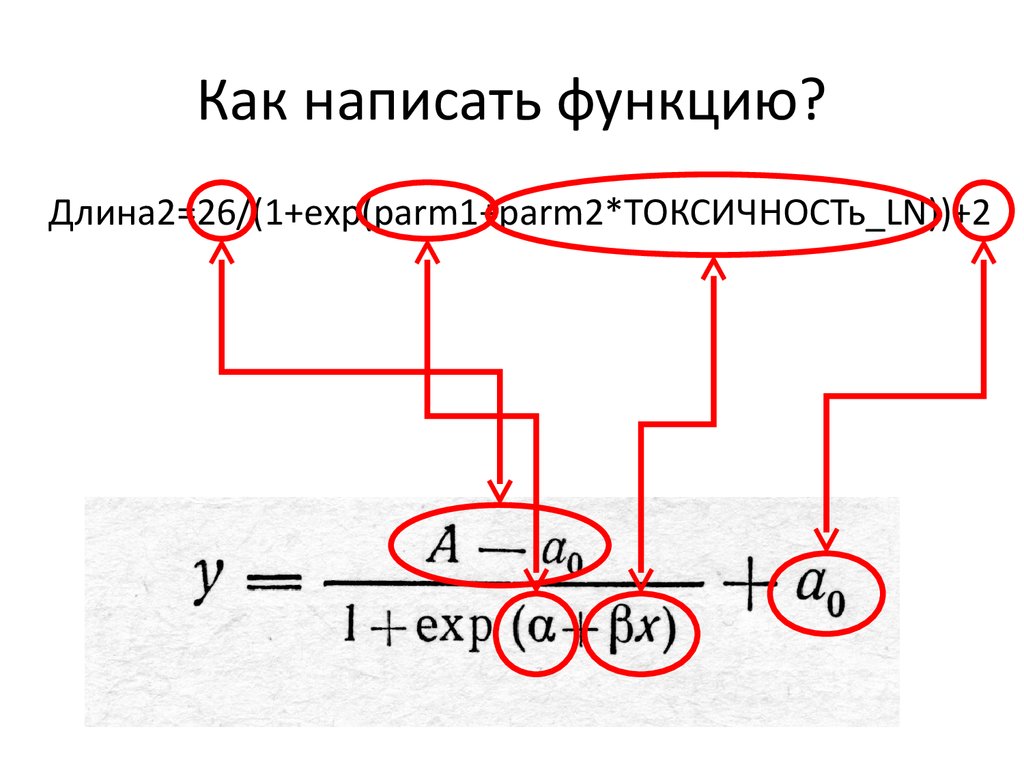
13. Как написать функцию?

Длина2=26/(1+exp(parm1+parm2*ТОКСИЧНОСТь_LN))+2

14. Общая логика вычислительных процедур при нелинейном оценивании в STATISTICA

• Не строгие решения функций;
• Итерации – последовательные вычисления,
приближающие качество описания (значения
коэффициентов) к исходным данным;
• Этим качеством иногда можно управлять;

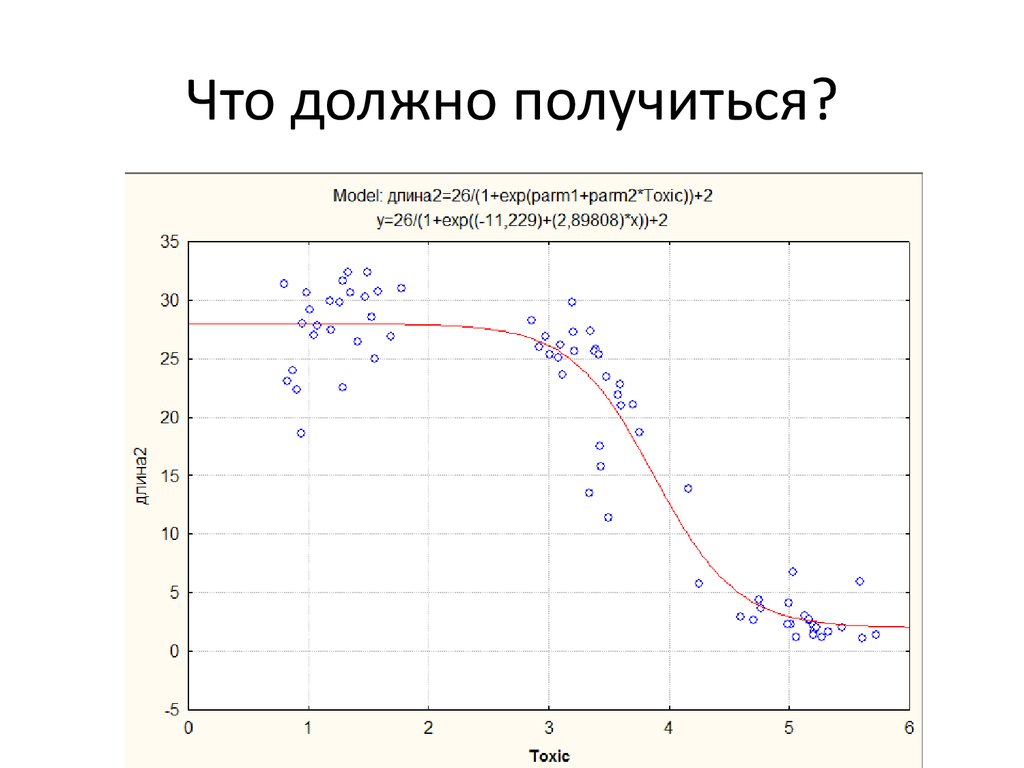
15. Что должно получиться?

16. Попробуем? Нахождение координат критических точек

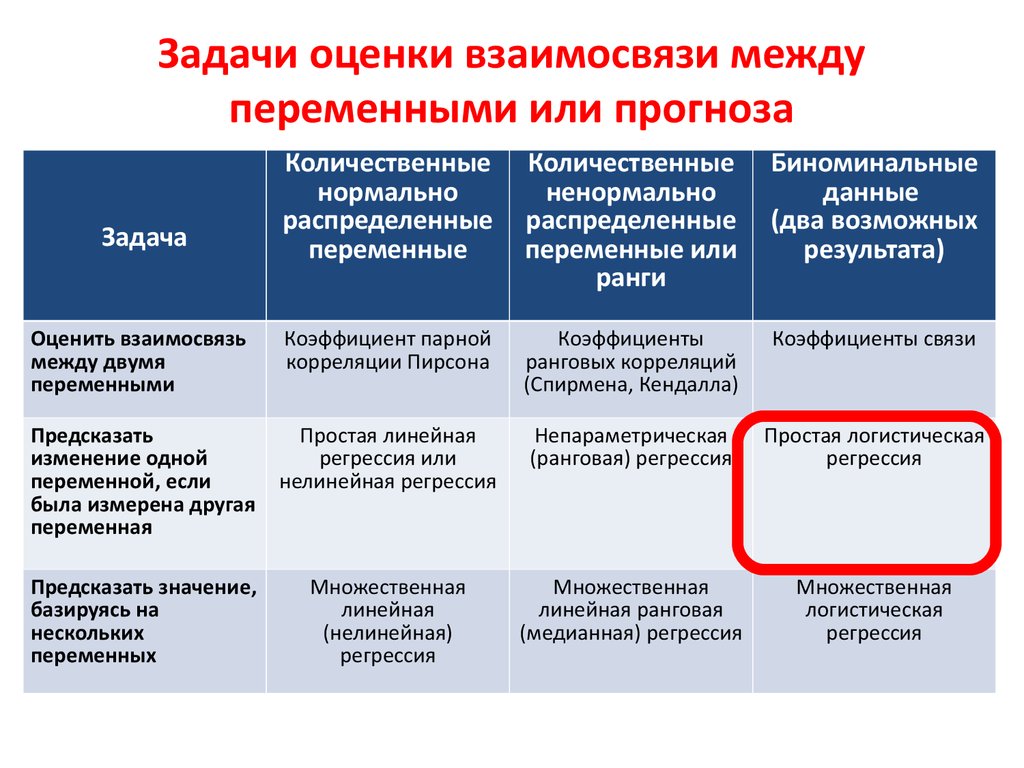
17. Задачи оценки взаимосвязи между переменными или прогноза

Количественные
нормально
распределенные
переменные
Количественные
ненормально
распределенные
переменные или
ранги
Биноминальные
данные
(два возможных
результата)
Оценить взаимосвязь
между двумя
переменными
Коэффициент парной
корреляции Пирсона
Коэффициенты
ранговых корреляций
(Спирмена, Кендалла)
Коэффициенты связи
Предсказать
изменение одной
переменной, если
была измерена другая
переменная
Простая линейная
регрессия или
нелинейная регрессия
Непараметрическая
(ранговая) регрессия
Простая логистическая
регрессия
Предсказать значение,
базируясь на
нескольких
переменных
Множественная
линейная
(нелинейная)
регрессия
Множественная
линейная ранговая
(медианная) регрессия
Множественная
логистическая
регрессия
Задача

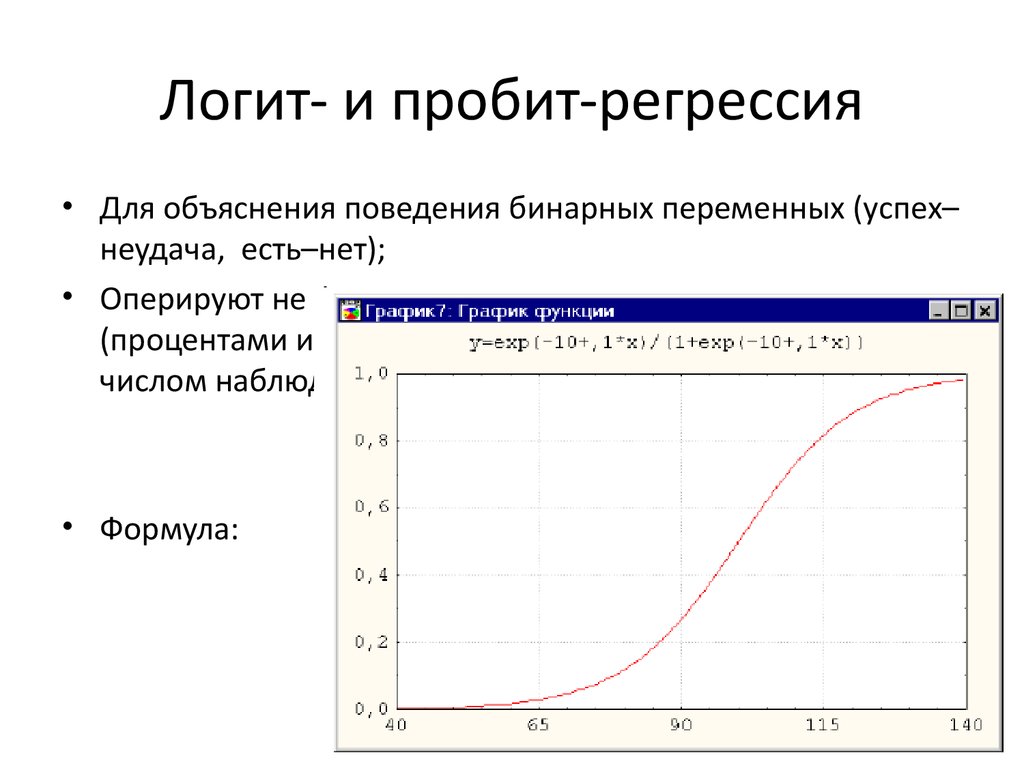
18. Логит- и пробит-регрессия

• Для объяснения поведения бинарных переменных (успех–
неудача, есть–нет);
• Оперируют не финальными относительными частотами
(процентами или долями), а как в случае с хи-квадратом,
числом наблюдений того или иного случая;
• Формула:

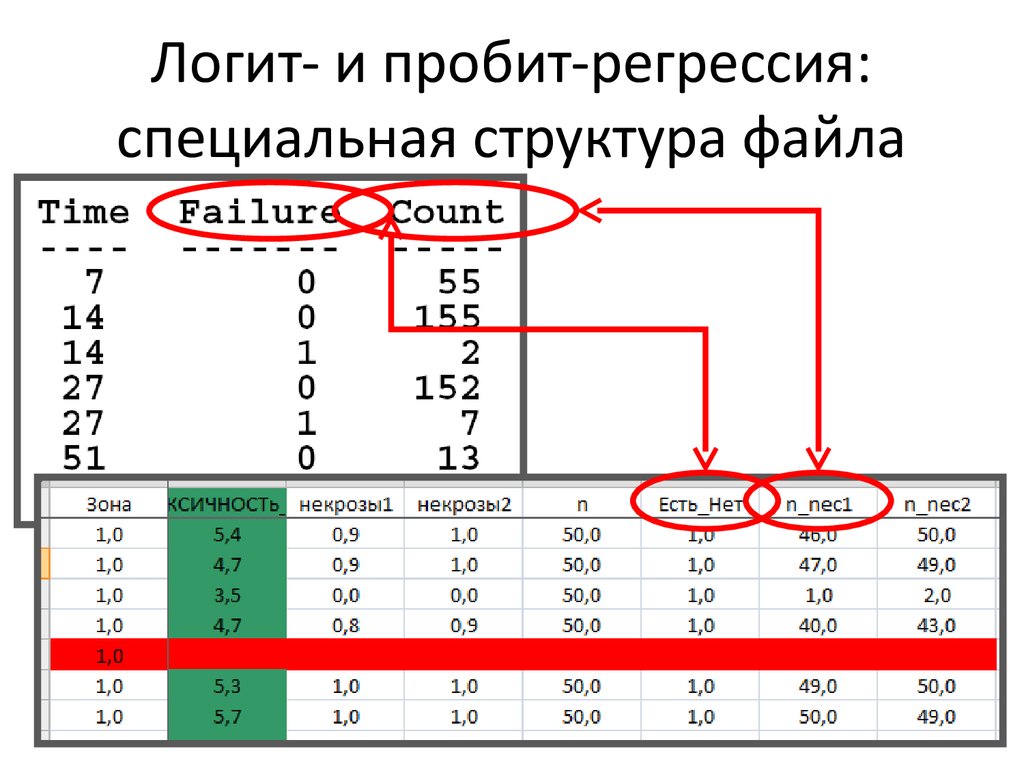
19. Логит- и пробит-регрессия: специальная структура файла

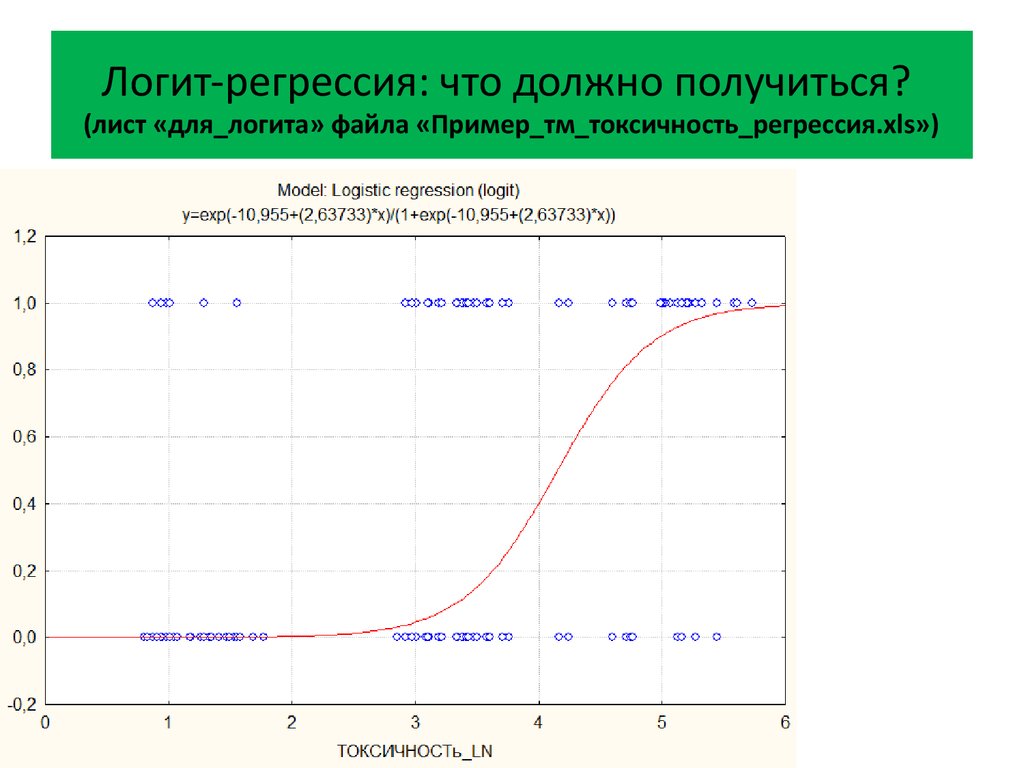
20. Логит-регрессия: что должно получиться? (лист «для_логита» файла «Пример_тм_токсичность_регрессия.xls»)

21. Задачи оценки взаимосвязи между переменными или прогноза

Количественные
нормально
распределенные
переменные
Количественные
ненормально
распределенные
переменные или
ранги
Биноминальные
данные
(два возможных
результата)
Оценить взаимосвязь
между двумя
переменными
Коэффициент парной
корреляции Пирсона
Коэффициенты
ранговых корреляций
(Спирмена, Кендалла)
Коэффициенты связи
Предсказать
изменение одной
переменной, если
была измерена другая
переменная
Простая линейная
регрессия или
нелинейная регрессия
Непараметрическая
(ранговая) регрессия
Простая логистическая
регрессия
Предсказать значение,
базируясь на
нескольких
переменных
Множественная
линейная
(нелинейная)
регрессия
Множественная
линейная ранговая
(медианная) регрессия
Множественная
логистическая
регрессия
Задача

22. Множественная регрессия: общая структура и предположения

Y = a + b1 * X + b2 * X2 + … + b3*X
n
• Линейности частных зависимостей;
• Нормальности всех переменных;
• Нескоррелированности независимых переменных;
• Не менее (7)10–20 независимых наблюдений на
каждый предиктор в модели;

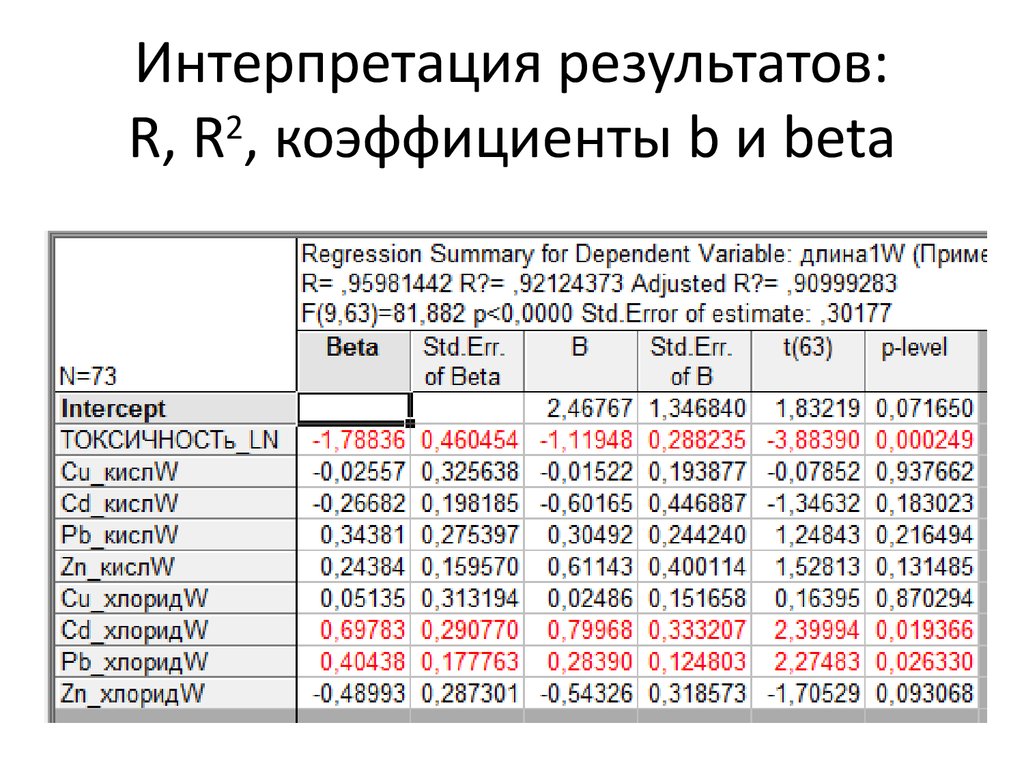
23. Интерпретация результатов: R, R2, коэффициенты b и beta

24. Методы пошагового отбора переменных

25. Гребневая регрессия

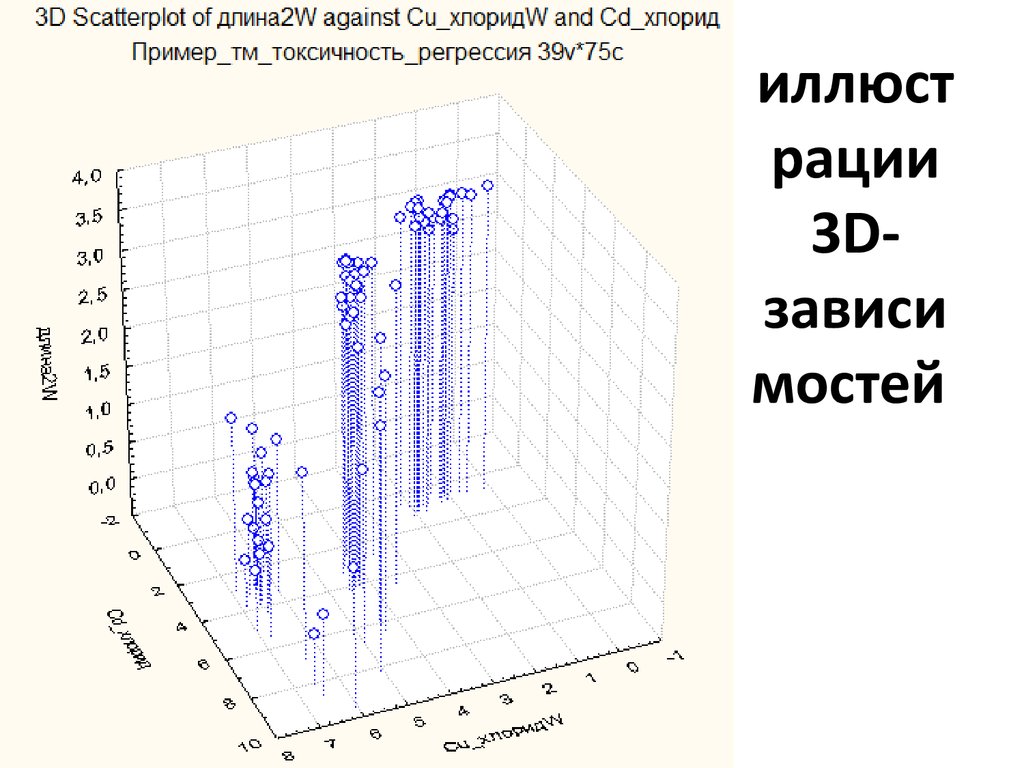
26. иллюстрации 3D-зависимостей

иллюст
рации
3Dзависи
мостей