Похожие презентации:
Затухающие и вынужденные колебания. Уравнение затухающих колебаний
1. ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
2. 1. УРАВНЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Во всякой реальной колебательнойсистеме имеются силы сопротивления,
действие которых приводит к
затуханию колебаний.
В простейшем и наиболее часто
встречающемся случае сила сопротивления пропорциональна скорости:
Fx* rVx rx mx kx rx
r
k
mx rx kx 0 x x x 0;
m
m
r
k
2 ;
02 x 2 x 02 x 0.
m
m
3. 2. РЕШЕНИЕ УРАВНЕНИЯ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
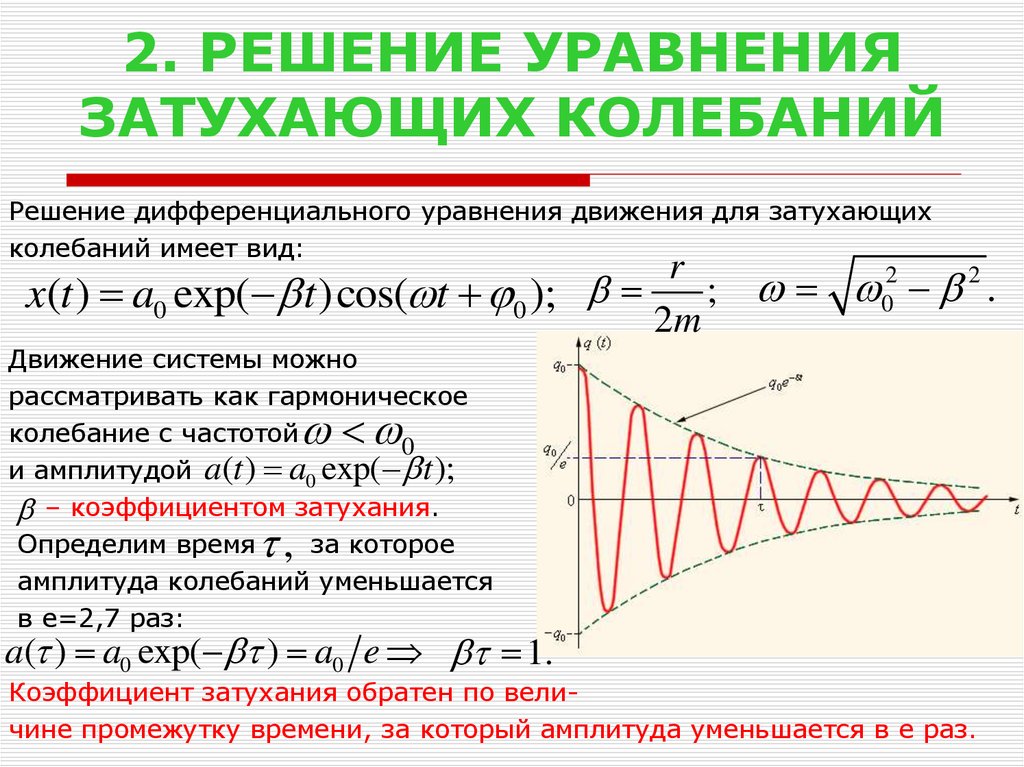
Решение дифференциального уравнения движения для затухающихколебаний имеет вид:
r
;
x(t ) a0 exp( t )cos( t 0 );
2m
.
2
0
2
Движение системы можно
рассматривать как гармоническое
колебание с частотой
0
и амплитудой a(t ) a0 exp( t );
– коэффициентом затухания.
Определим время
за которое
амплитуда колебаний уменьшается
в e=2,7 раз:
,
a( ) a0 exp( ) a0 e 1.
Коэффициент затухания обратен по величине промежутку времени, за который амплитуда уменьшается в e раз.
4. 3. ЛОГАРИФМИЧЕСКИЙ ДЕКРЕМЕНТ ЗАТУХАНИЯ
Отношение амплитуд, соответствующих моментам времени,различающимся на период, называют декрементом затухания
a (t )
a0 exp( t )
exp( T ).
a (t T ) a0 exp (t T )
Логарифм отношения амплитуд, отстоящих на период, называется
логарифмическим декрементом затухания
a (t )
T
1
ln
T
.
a (t T )
Ne
T
2
02 2
T0
2
0
.
5. 4. ДОБРОТНОСТЬ
Для характеристики потерь энергии в колебательной системеиспользуется величина, называемая добротностью.
W
Q 2
W
Добротность в
раз превышает число колебаний Ne , совершаемых
системой за время
в течение которого амплитуда колебаний
уменьшается в e 2,718 раз.
,
Q N e
6. 5. ЭНЕРГИЯ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Полная механическая энергия колебательной системы складывается из2
2
кинетической и потенциальной энергии, то есть E kx 2 mV
x
Для затухающих колебаний
t
2.
cos( t 0 );
Vx x a0 e t cos( t 0 ) a0 e t sin( t 0 )
x a0e
ka02
E
exp( 2 t ) 1 sin(2 t 2 0 ) ; arctg .
2
0
Скорость изменения энергии системы равна мощности, развиваемой
силой сопротивления:
dE dt Fx* Vx ; Fx* rVx dE dt rVx2 .
В моменты времени, для которых скорость тела равна нулю мощность
силы сопротивления также равна нулю.
Во все остальные моменты мощность отрицательна и энергия убывает.
7. 6. УРАВНЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
Рассмотрим движение тела, на которое действуют: возвращающая сила*
(квазиупругая) Fx kx; сила сопротивления Fx rVx ; внешняя
гармоническая вынуждающая сила с амплитудой F0 : Fx F0 cos( t ).
Уравнение движения в данном случае будет иметь вид:
max kx rVx F0 cos( t ) mx rx kx F0 cos( t )
r
k
2 F0
2
;
x 2 x x f 0 cos( t ).
0 ; f 0
m
m
m
2
0
f0
– амплитуда ускорения и
- частота внешней вынуждающей силы.
8. 7. РЕШЕНИЕ УРАВНЕНИЯ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
Уравнение движения вынужденных колебаний является неоднородным:2
0
0
x 2 x x f cos( t ).
Согласно известной математической теореме, общее решение неоднородного дифференциального уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного
уравнения, то есть x(t ) x (t ) x (t ).
o
ч
xo (t ) a0 exp( t )cos( t 0 ); 02 2
– частота свободных
затухающих колебаний.
2
xч (t )
cos t arctg 2
.
2
2
2 2
2 2
0
( 0 ) 4
F0 m
9. 8. АНАЛИЗ ОБЩЕГО РЕШЕНИЯ
x(t ) a0 et
cos
2
t 0
cos t arctg 2
.
2
2
2 2
2 2
0
( 0 ) 4
2
0
2
F0 m
Первое слагаемое описывает собственные затухающие колебания системы.
Оно играет заметную роль только в начальной стадии процесса, при
установлении колебаний. С течением времени из-за множителя exp( t )
роль первого слагаемого уменьшается и им
можно пренебречь, оставляя в решении лишь
второе слагаемое. Оно представляет собой
гармоническое колебание с частотой внешней
вынуждающей силы
.
10. 9. РЕЗОНАНС
F m0
Амплитуда вынужденных колебаний
A
.
2
2 2
2 2
определяется выражением
( 0 ) 4
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной
системы частоте амплитуда достигает максимального значения. Это явление называется резонансом, а соответствующая частота - резонансной.
Резонансную частоту определим из условия
максимального значения амплитуды
или
минимального значения для подкоренного
выражения в знаменателе. Продифференцировав
это выражение по
и приравняв нулю, получим
условие, определяющее резонансную частоту:
A
4( 02 р2 ) р 8 2 р 0
р 02 2 2 .









 Физика
Физика








