Похожие презентации:
Преобразования графика функции f(x)=x2
1. Преобразования графика функции f(x)=x2
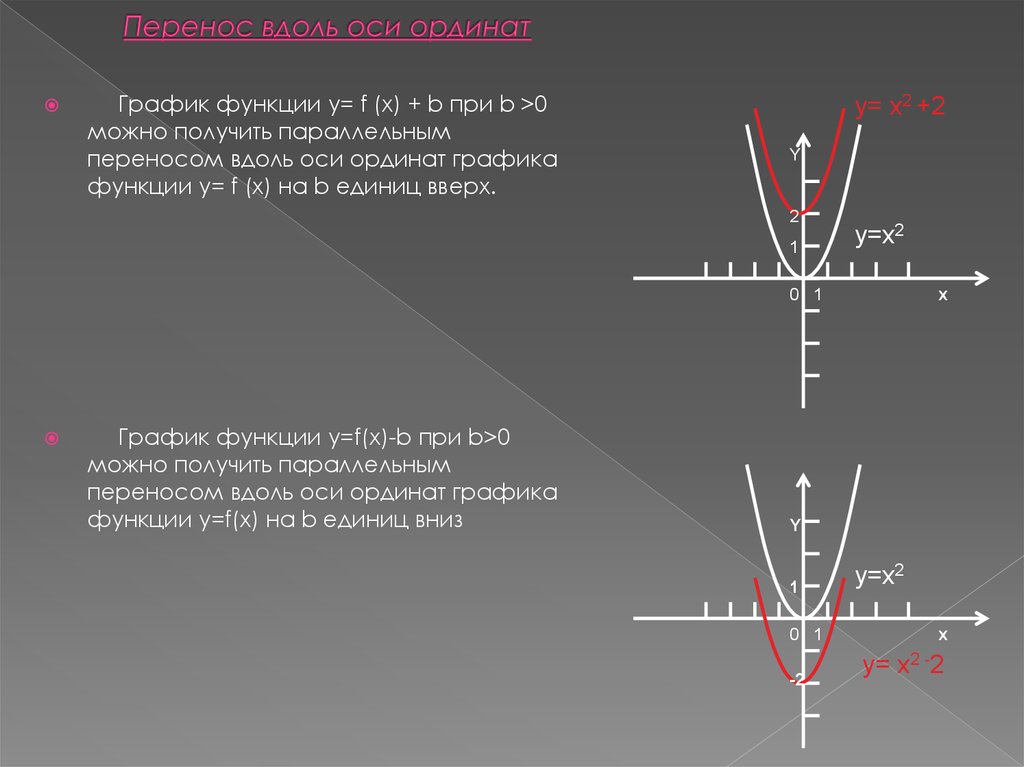
2. Перенос вдоль оси ординат
График функции y= f (x) + b при b >0можно получить параллельным
переносом вдоль оси ординат графика
функции y= f (x) на b единиц вверх.
y= x2 +2
Y
2
1
y=x2
0 1
График функции y=f(x)-b при b>0
можно получить параллельным
переносом вдоль оси ординат графика
функции y=f(x) на b единиц вниз
x
Y
1
0 1
-2
y=x2
x
y= x2 -2
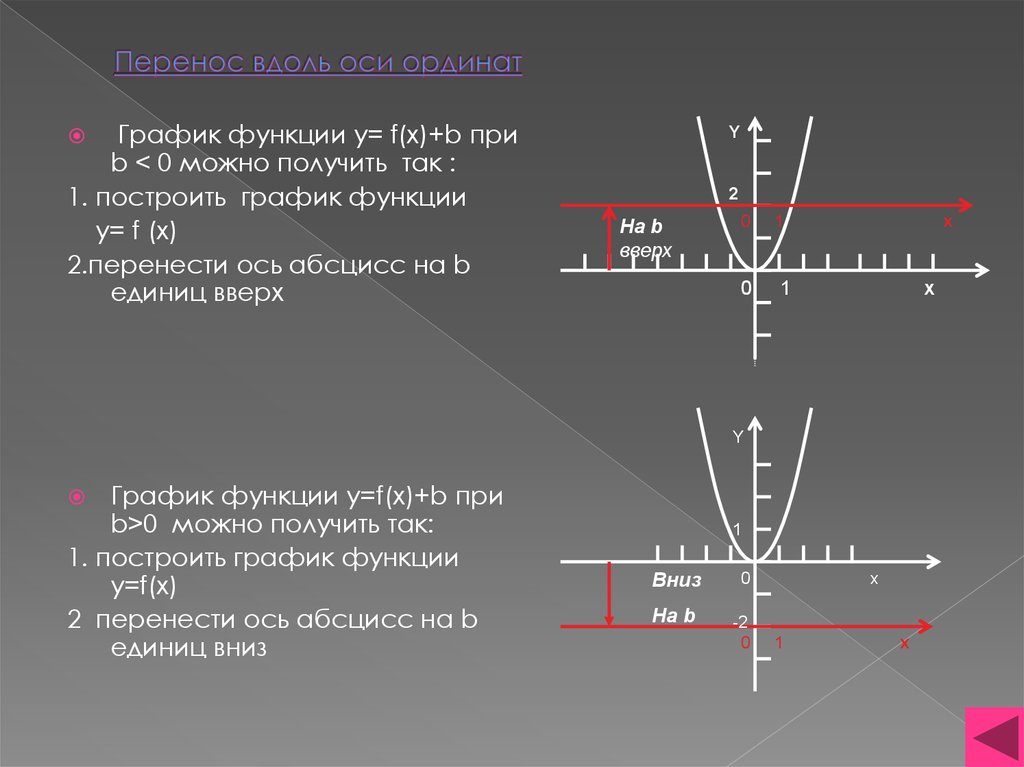
3. Перенос вдоль оси ординат
График функции y= f(x)+b приb < 0 можно получить так :
1. построить график функции
y= f (x)
2.перенести ось абсцисс на b
единиц вверх
Y
2
На b
вверх
0
0
1
x
1
x
Y
График функции y=f(x)+b при
b>0 можно получить так:
1. построить график функции
y=f(x)
2 перенести ось абсцисс на b
единиц вниз
1
Вниз
На b
0
-2
0
x
1
x
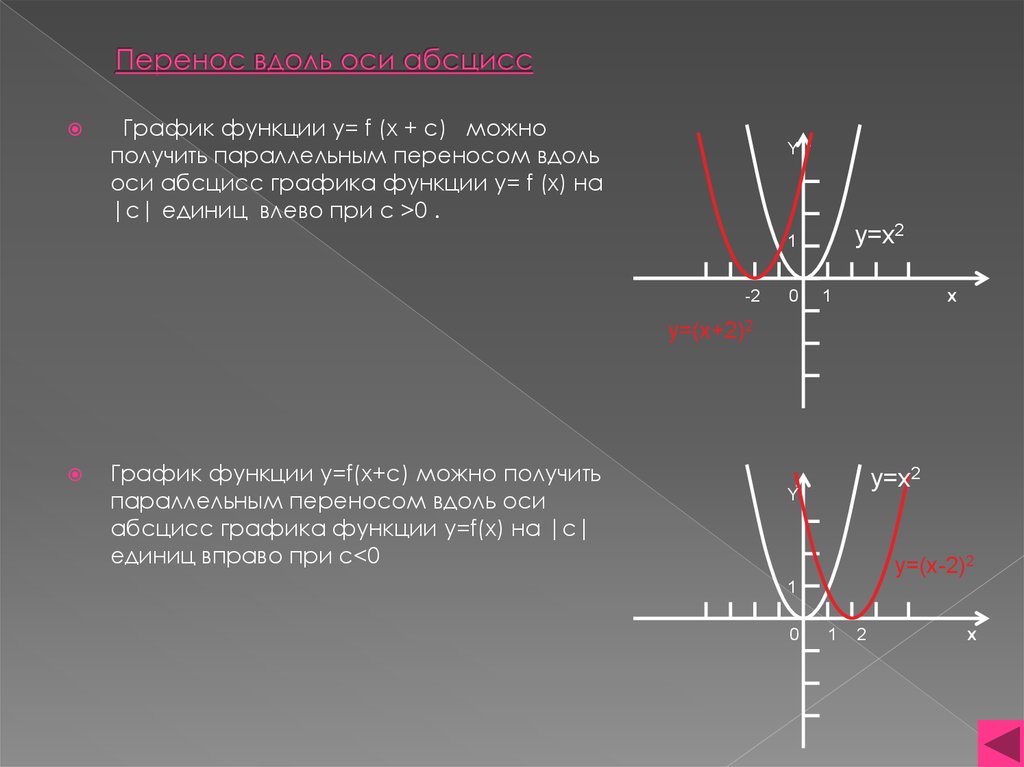
4. Перенос вдоль оси абсцисс
График функции y= f (x + c) можнополучить параллельным переносом вдоль
оси абсцисс графика функции y= f (x) на
|c| единиц влево при c >0 .
Y
y=x2
1
-2
0
1
x
y=(x+2)2
График функции y=f(x+c) можно получить
параллельным переносом вдоль оси
абсцисс графика функции y=f(x) на |c|
единиц вправо при c<0
y=x2
Y
y=(x-2)2
1
0
1
2
x
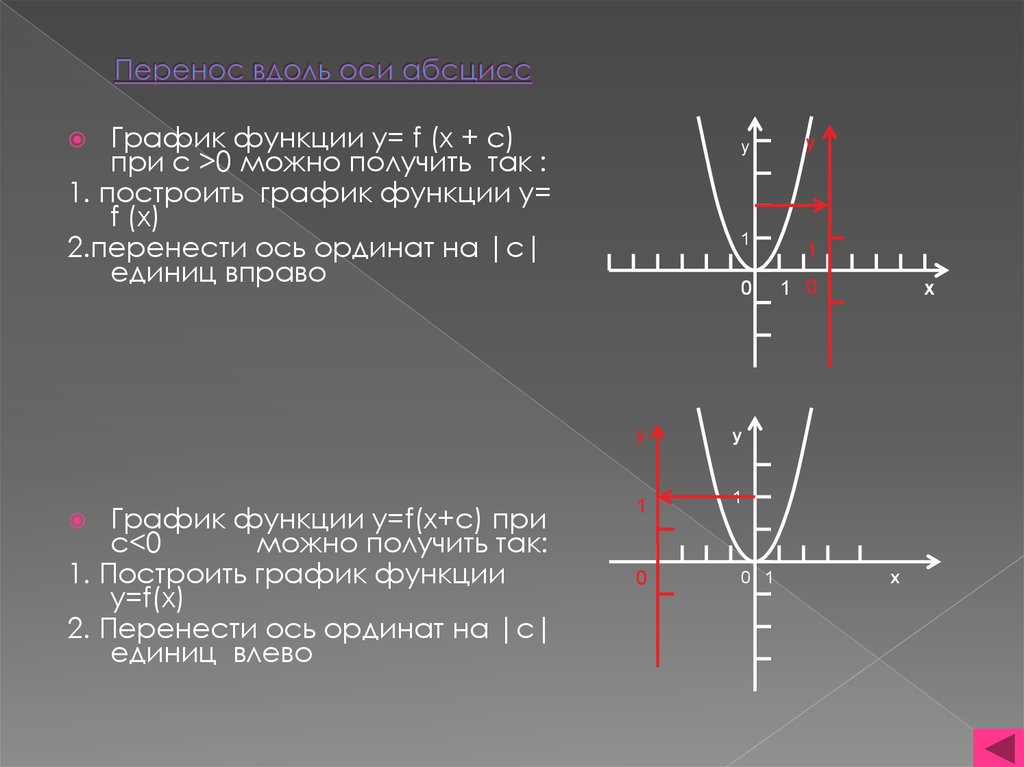
5. Перенос вдоль оси абсцисс
График функции y= f (x + c)при c >0 можно получить так :
1. построить график функции y=
f (x)
2.перенести ось ординат на |c|
единиц вправо
График функции y=f(x+c) при
c<0
можно получить так:
1. Построить график функции
y=f(x)
2. Перенести ось ординат на |c|
единиц влево
y
1
0
y
y
1
1
0
0 1
y
1
1 0
x
x
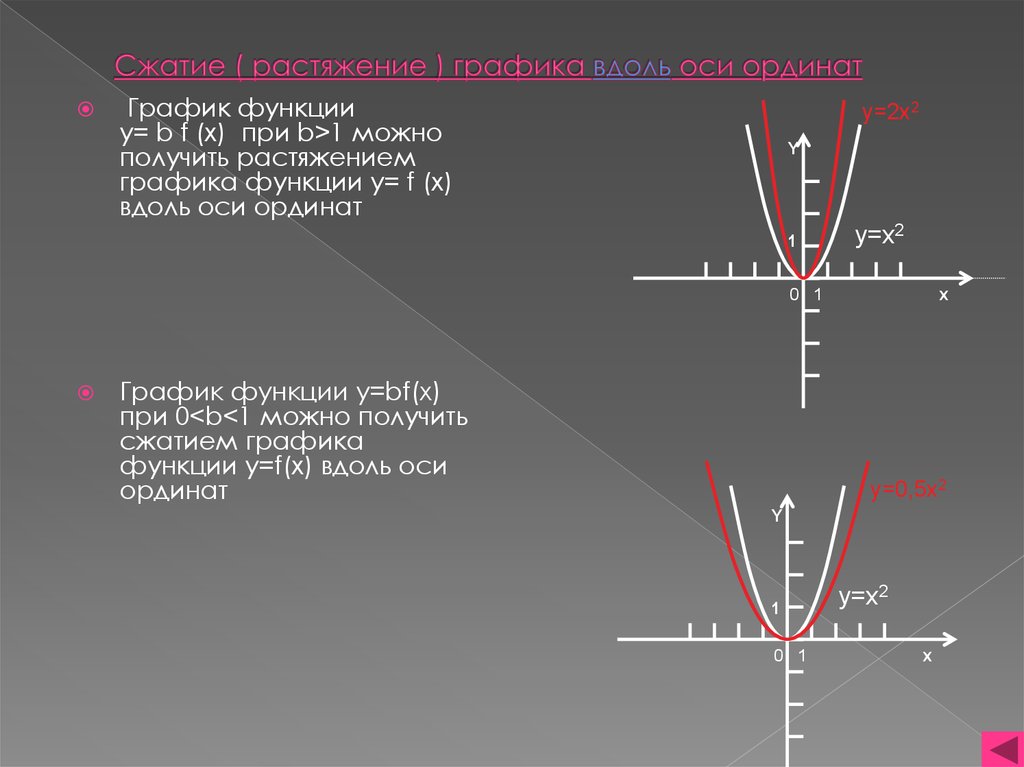
6. Сжатие ( растяжение ) графика вдоль оси ординат
График функцииy= b f (x) при b>1 можно
получить растяжением
графика функции y= f (x)
вдоль оси ординат
y=2x2
Y
1
y=x2
0 1
График функции y=bf(x)
при 0<b<1 можно получить
сжатием графика
функции y=f(x) вдоль оси
ординат
x
y=0,5x2
Y
1
0 1
y=x2
x
7. Симметрия относительно оси абсцисс
Чтобы построить график фунуции y= -f(x):1. Строим график функции y=f(x)
2. Отражаем его симметрично
относительно оси абсцисс.
y=x2
0 1
x
y=-x2
8. график функции y = f(|x|), y = |f(x)|
график функции y = f(|x|) получается из графика функции y =f(x) следующим преобразованием:
1) точки графика, имеющие неотрицательные абсциссы –
неподвижны;
2) точки графика, имеющие отрицательные абсциссы
заменяются на точки, полученные из неподвижных
отражением относительно оси y.
график функции y = |f(x)| получается из графика функции y =
f(x) следующим преобразованием:
1) точки графика, имеющие неотрицательные ординаты –
неподвижны;
2) точки графика, имеющие отрицательные ординаты,
отражаются относительно оси x.
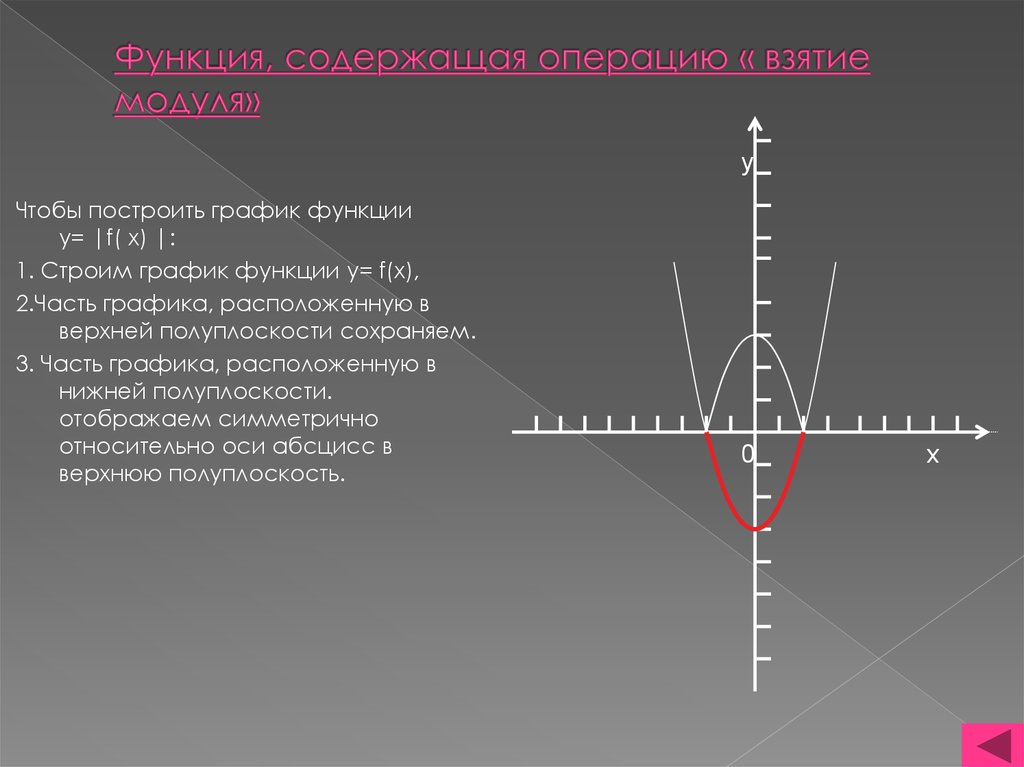
9. Функция, содержащая операцию « взятие модуля»
yЧтобы построить график функции
y= |f( x) |:
1. Строим график функции y= f(x),
2.Часть графика, расположенную в
верхней полуплоскости сохраняем.
3. Часть графика, расположенную в
нижней полуплоскости.
отображаем симметрично
относительно оси абсцисс в
верхнюю полуплоскость.
0
x



 Математика
Математика








