Похожие презентации:
Если я знаю, что знаю мало, я добьюсь того, чтобы знать больше
1.
Если я знаю, что знаю мало,я добьюсь того, чтобы знать
больше.
В. И. Ленин. (о знаниях)
2. Вычисли:
cos ;3
sin
2
sin0;
;
sin
cos ;
6
6
;
sin
3
;
5
sin ;
6
Найти область значений функции:
y x 2 x;
y x 4;
y x 3;
y x 5
2
2
3.
12
3
4
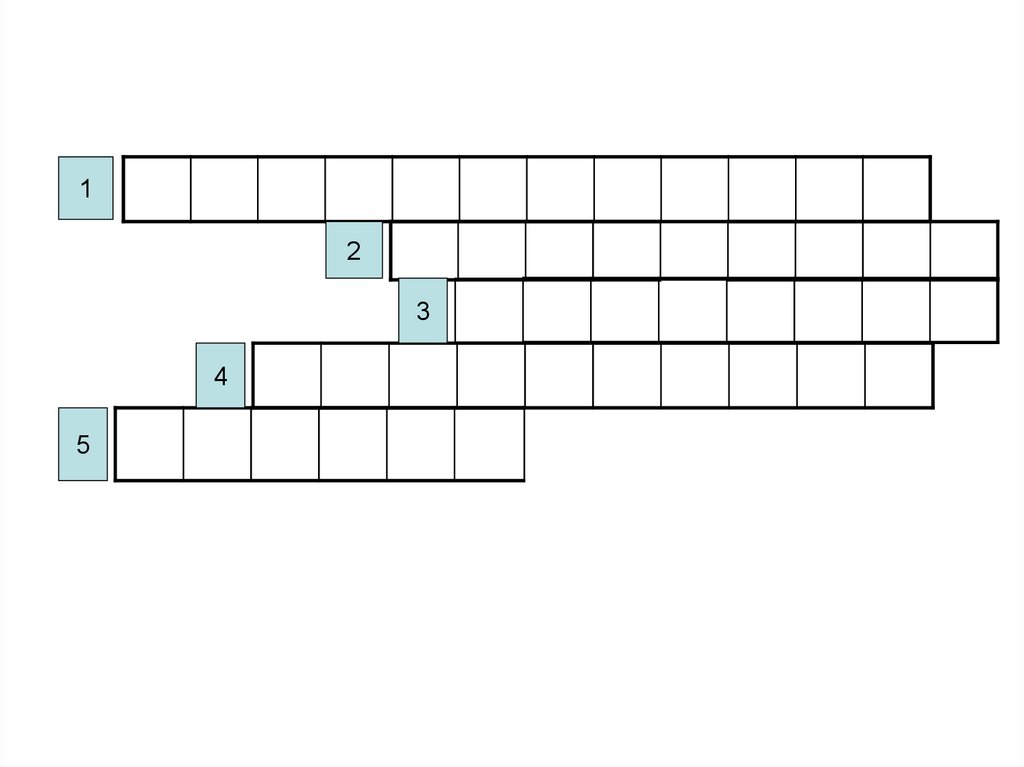
5
4.
1В
О З
Р
А
2
3
4
5
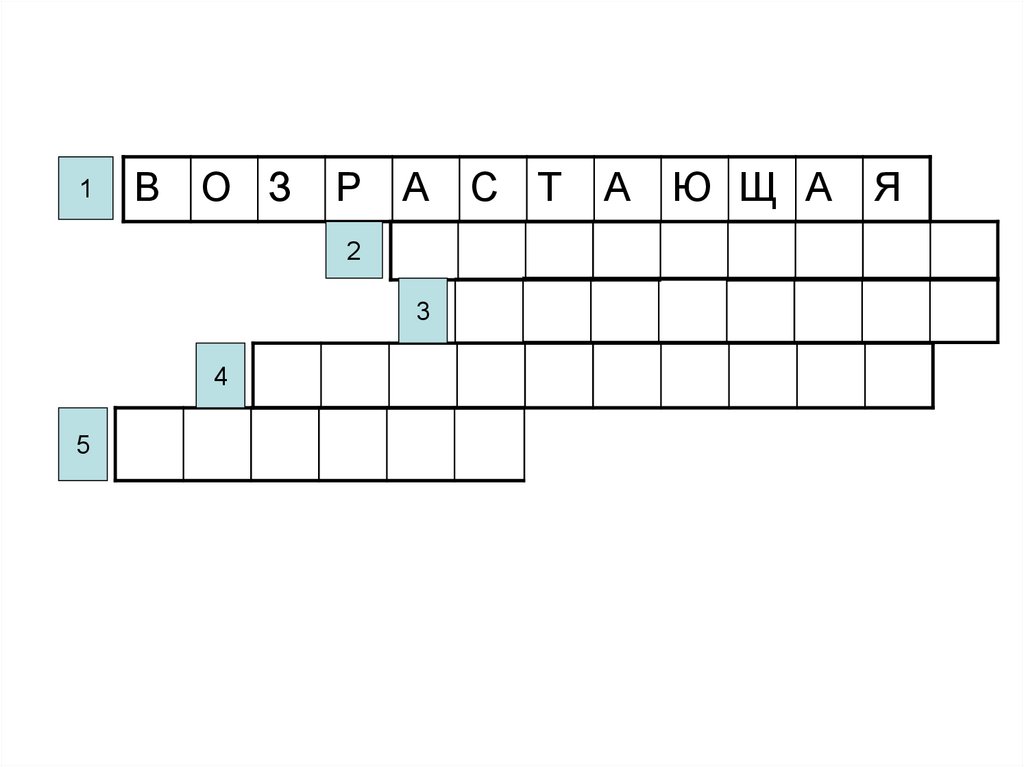
С Т
А
Ю Щ А
Я
5.
1В
О З
Р
А
С Т
2
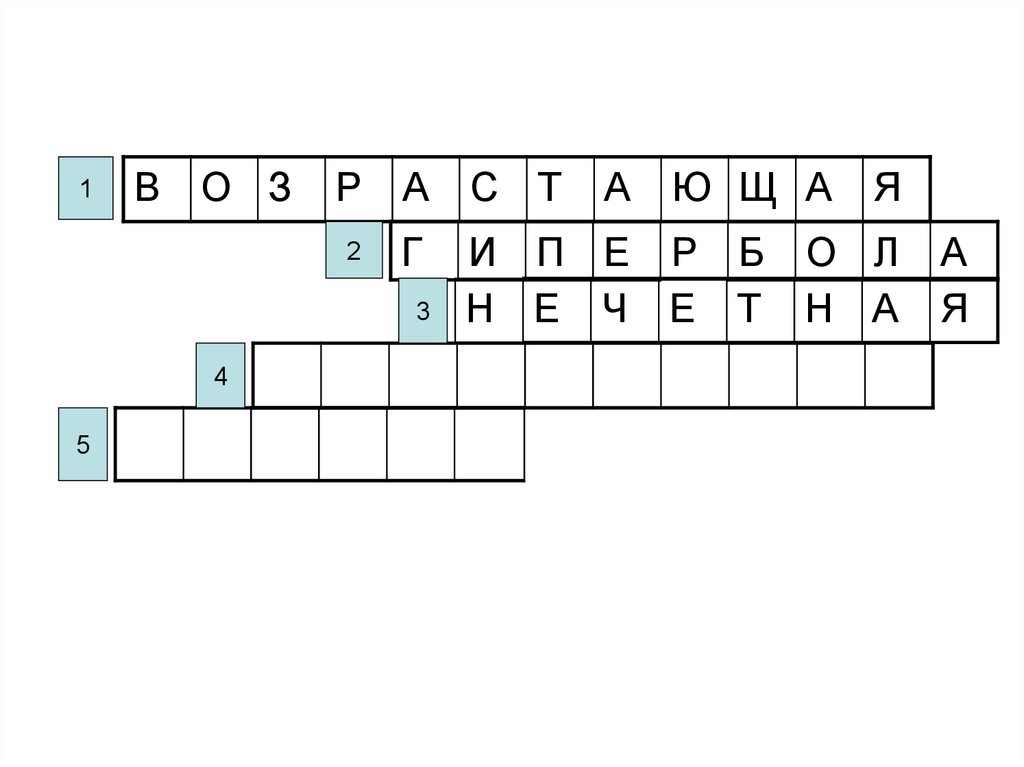
Г
И П Е
3
4
5
А
Ю Щ А
Р
Б
Я
О Л
А
6.
1В
О З
Р
А
С Т
2
Г
И П Е Р Б
Н Е Ч Е Т
3
4
5
А
Ю Щ А
Я
О Л
Н А
А
Я
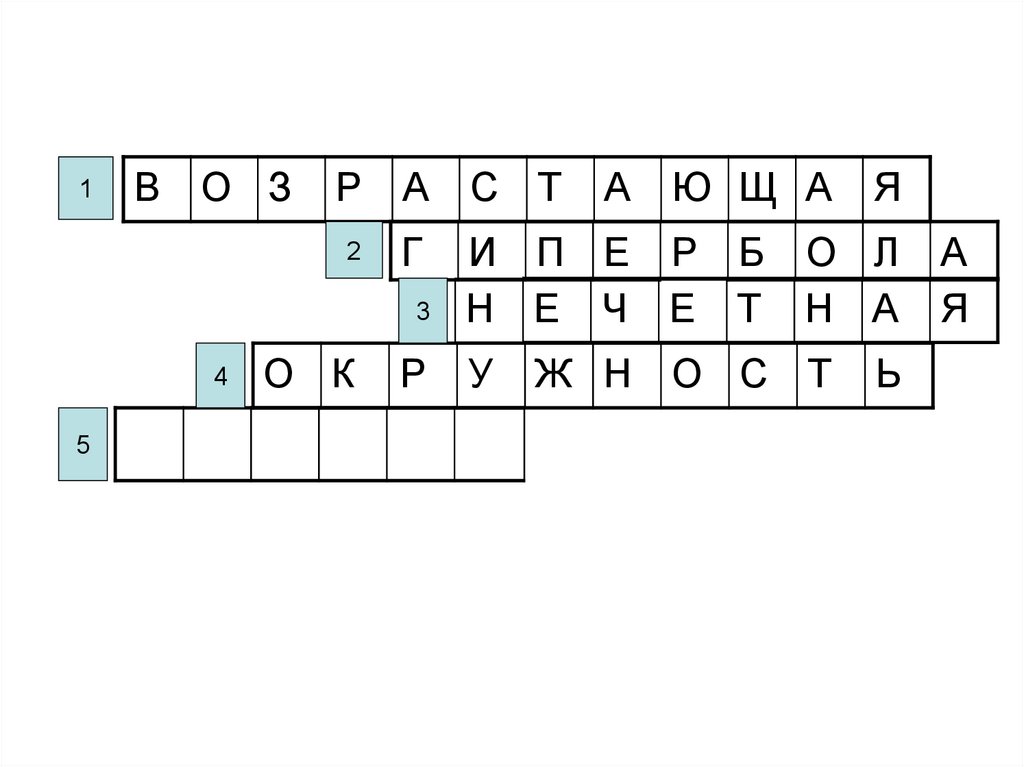
7.
1В
О З
Р
А
С Т
2
Г
И П Е Р Б
Н Е Ч Е Т
3
4
5
О К
Р
У
А
Ю Щ А
Я
О Л
Н А
Ж Н О С Т
Ь
А
Я
8.
1В
О З
Р
А
С Т
2
Г
И П Е Р Б
Н Е Ч Е Т
3
4
5
Р
А
О К
Д
Р
У
И У
С
А
Ю Щ А
Я
О Л
Н А
Ж Н О С Т
Ь
А
Я
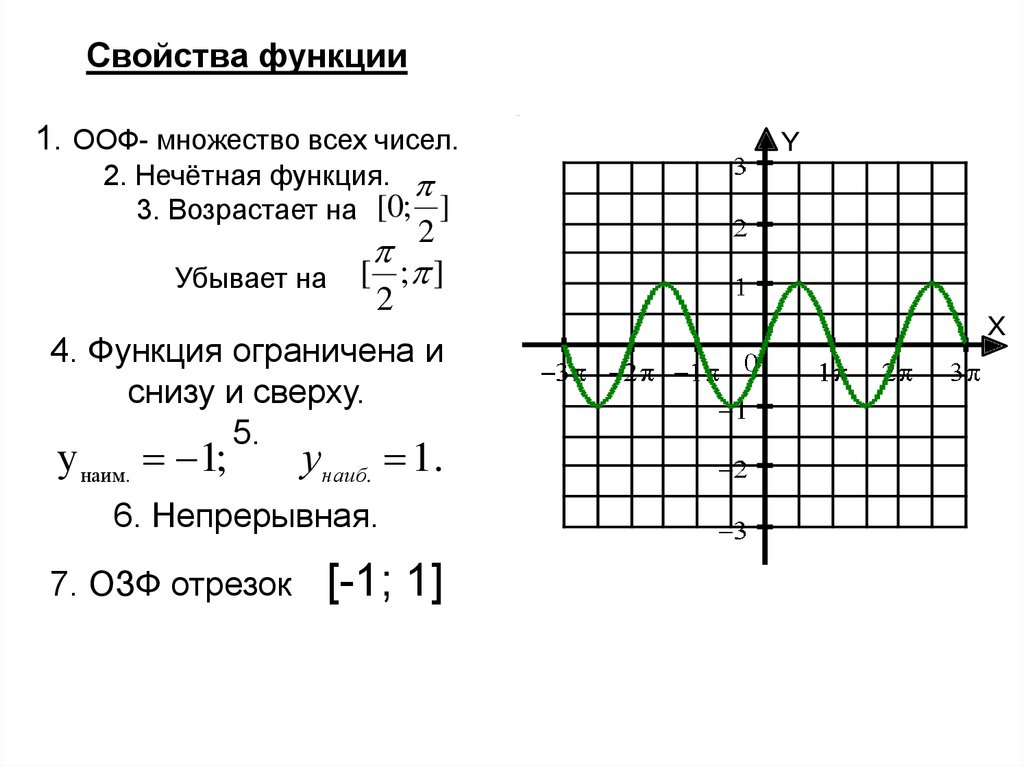
9. Свойства функции 1. ООФ- множество всех чисел. 2. Нечётная функция. 3. Возрастает на Убывает на 4. Функция ограничена и снизу и
Свойства функции1. ООФ- множество всех чисел.
2. Нечётная функция.
3. Возрастает на [0; ]
2
[
; ]
Убывает на
2
4. Функция ограничена и
снизу и сверху.
5.
унаим. 1;
унаиб. 1.
6. Непрерывная.
7. ОЗФ отрезок
[-1; 1]
Y
X
10.
Р.Декарт (1596-1650г.г.)2 3
Ф.Виет (1540-1603)
sin
6
5i 1
2
Л.Эйлер (1707-1783)
Пифагор (около 580г.
до н.э.- 500г. до н.э.
2
cos
3
11.
• Тригонометрические функции возниклив Древней Греции в связи с
исследованиями в астрономии и
геометрии. Понятия синуса и косинуса
встречаются уже в 3 веке до н.э. в
работах Евклида, Архимеда и др.
• Современную форму тригонометрии
придал Л. Эйлер. Ему принадлежат
определения тригонометрических
функций и принятая в наши дни
символика.
12.
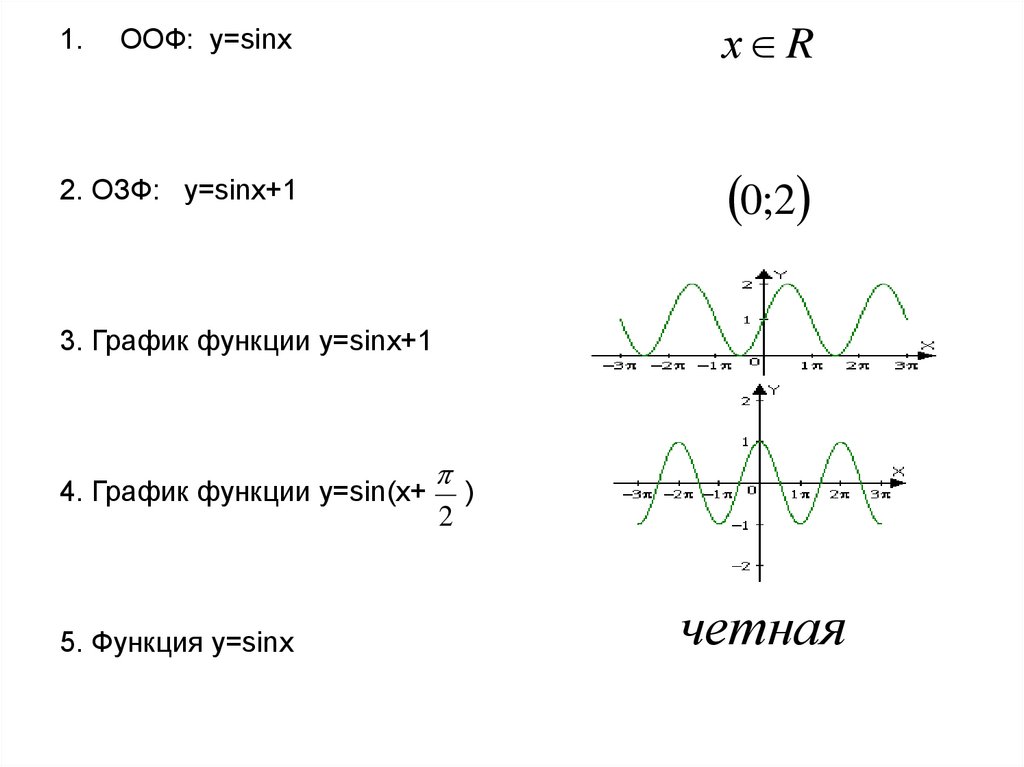
ООФ: у=sinxх R
2. ОЗФ: у=sinx+1
0;2
1.
3. График функции у=sinx+1
4. График функции у=sin(x+
5. Функция y=sinx
)
2
четная






 Математика
Математика








