Похожие презентации:
Степенная функция
1. Степенная функция
Урок обобщенияПрезентацию подготовила и
выполнила Шурыгина И.В.
2. Эпиграфом нашего урока являются слова А. Эйнштейна:
“Весь наш предшествующий опытприводит к убеждению,
что природа является осуществлением того,
что математически проще всего представить”.
3. Цели урока
Повторить свойства и график степеннойфункции;
закрепить навыки построения графиков и их
описания с использованием программы
«Живая геометрия»;
продолжить работу над умением
анализировать поставленную задачу,
предполагаемый результат и обобщать;
Воспитывать чувство взаимовыручки,
коллективизма.
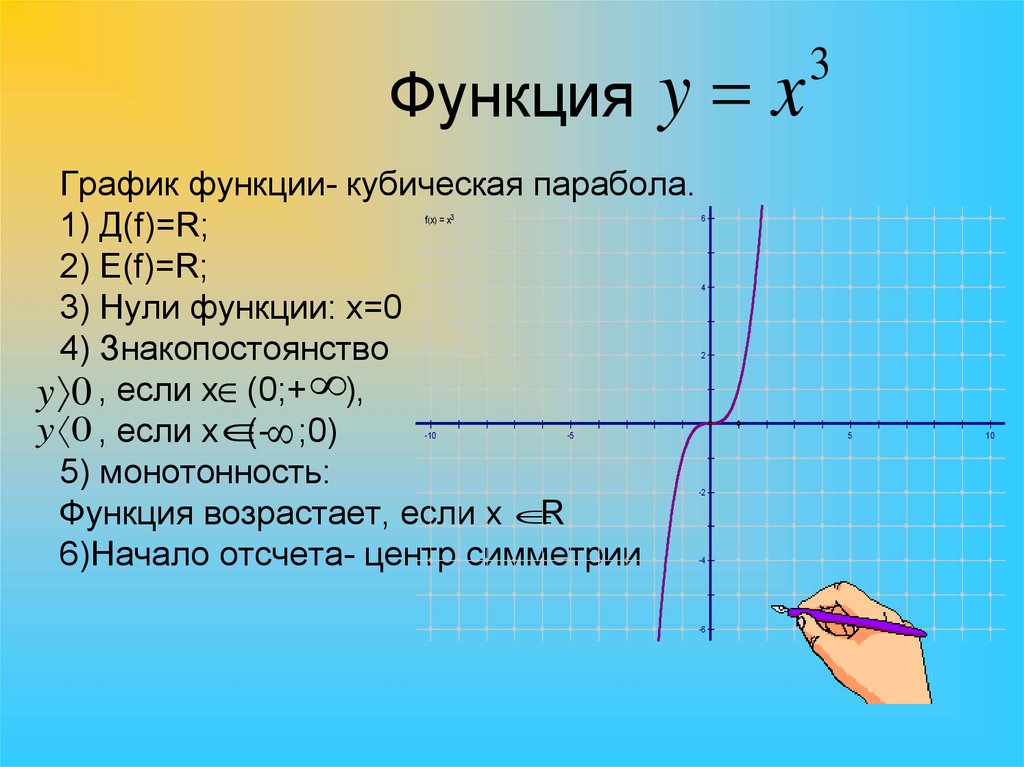
4. Функция
y xГрафик функции- кубическая парабола.
1) Д(f)=R;
2) E(f)=R;
3) Нули функции: x=0
4) Знакопостоянство
y 0 , если x (0;+ ),
y 0 , если x (- ;0)
5) монотонность:
Функция возрастает, если x
R
6)Начало отсчета- центр симметрии
f x = x3
-10
3
6
4
2
-5
5
-2
-4
-6
10
5.
y ( x a) b3
Число a- отвечает за перемещение вдоль оси ОХ;
если а 0,
то влево на а единиц от 0;
если а 0,
то вправо на а единиц от 0.
6
f x = x3
g x = x-3 3+2
4
2
Число b-отвечает за перемещение вдоль оси OY;
если b 0,
то вверх на b единиц от 0 ;
если b 0,
то вниз на b единиц от 0.
-10
5
-5
-2
-4
-6
10
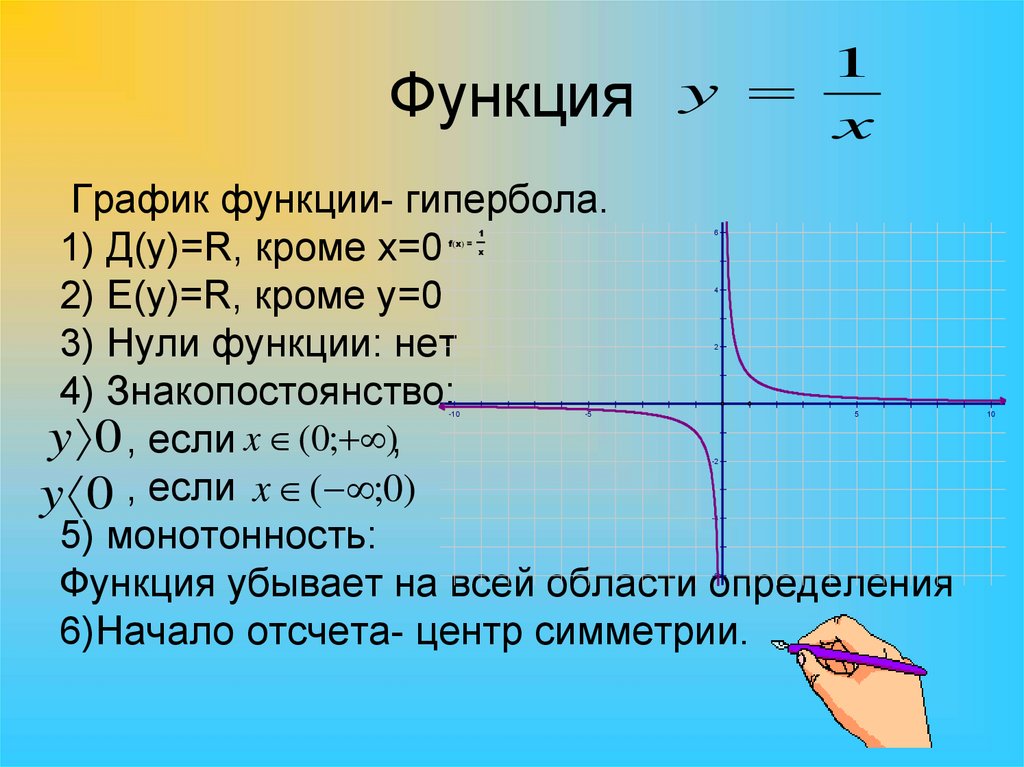
6. Функция
1y
x
График функции- гипербола.
1) Д(y)=R, кроме х=0
2) E(y)=R, кроме y=0
3) Нули функции: нет
4) Знакопостоянство:
y 0 , если x (0; ),
y 0 , если x ( ;0)
5) монотонность:
Функция убывает на всей области определения
6)Начало отсчета- центр симметрии.
f x =
1
6
x
4
2
-10
-5
5
-2
-4
-6
10
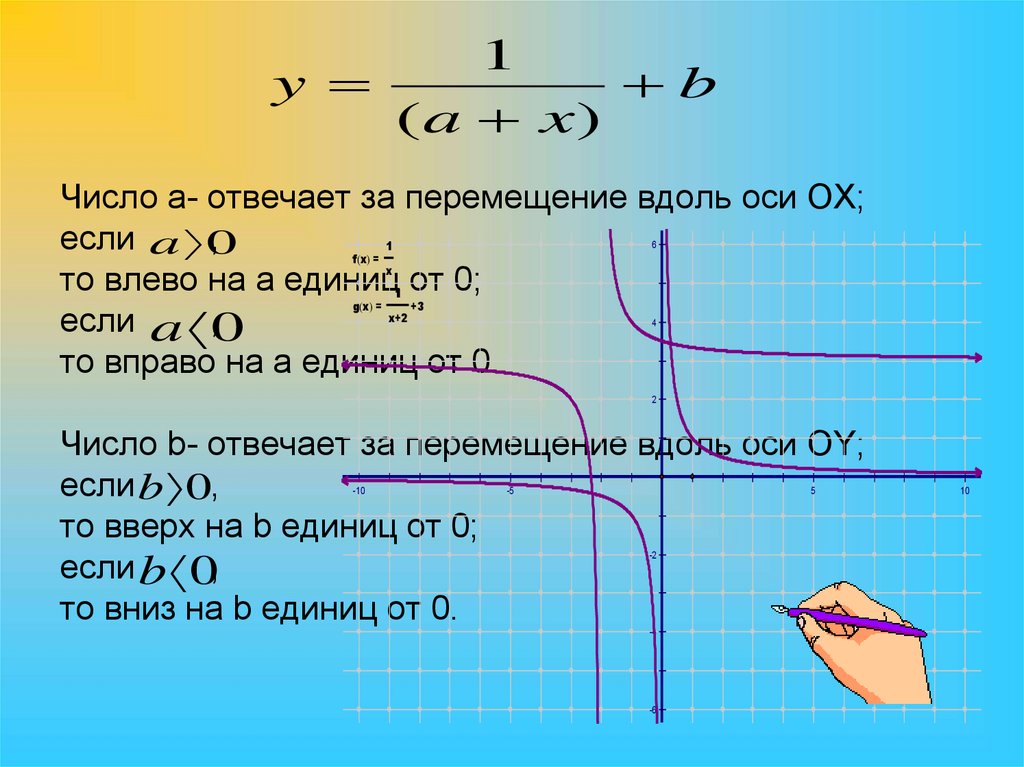
7.
1y
b
(a x)
Число а- отвечает за перемещение вдоль оси OX;
если a 0
,
то влево на a единиц от 0;
если a ,0
то вправо на а единиц от 0.
f x =
g x =
1
6
x
1
x+2
+3
4
2
Число b- отвечает за перемещение вдоль оси OY;
если b 0,
то вверх на b единиц от 0;
если b 0,
то вниз на b единиц от 0.
-10
-5
5
-2
-4
-6
10
8. Функция
y1) Д(y)= x 0;
2)E(y)= y 0;
3) Нули функции x=0
4) Знакопостоянство: y 0 ,
если x 0;
5) монотонность:
Функция возрастает,
если x 0;
1
f x = x
-10
x
6
2
4
2
5
-5
-2
-4
-6
10
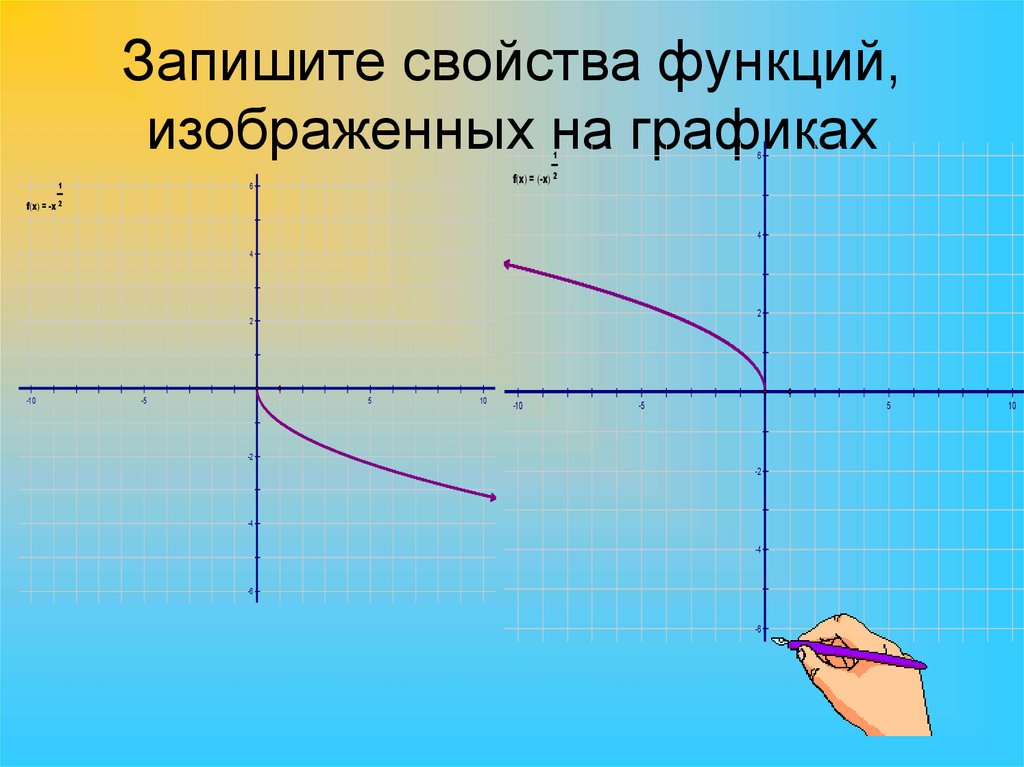
9. Запишите свойства функций, изображенных на графиках
11
f x = -x
6
f x = -x 2
6
2
4
4
2
2
-10
-5
5
10
-10
-5
5
-2
-2
-4
-4
-6
-6
10
10.
1f x = - -x
6
2
4
2
-10
-5
5
-2
-4
-6
10
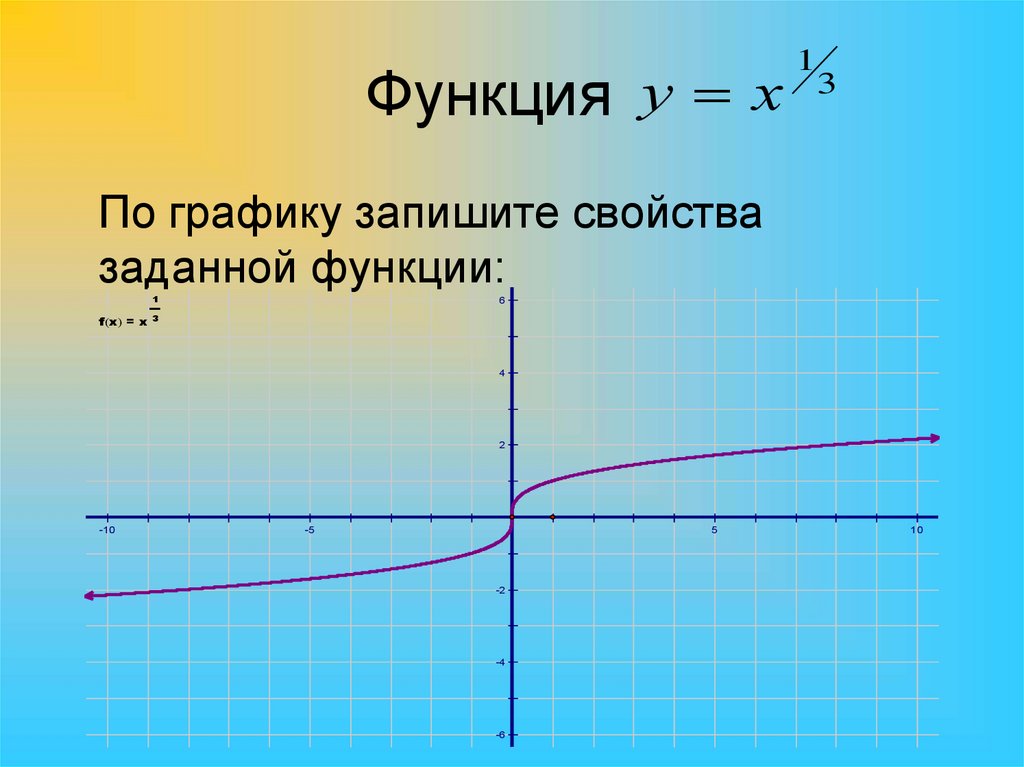
11. Функция
у х1
3
По графику запишите свойства
заданной функции:
1
f x = x
6
3
4
2
-10
-5
5
-2
-4
-6
10
12. Постройте графики заданных функций
y x3 3y ( x 4) 3 2
1
y
2
x
2
y
3
x 1
y
x 3
y
x 4 2
y
x 3
y
x 1 2
y
3
x 1 3
y
3
x 4
13. Итог урока:
Построение графика какой функции мысегодня с вами повторили?
Испытывали ли вы трудности в
построении графиков и описания их?
Были ли восполнены пробелы в ваших
знаниях?
14. Домашнее задание:
Составить и построить графикистепенной функции на каждый вид по 2
графика.
Всем спасибо за работу.





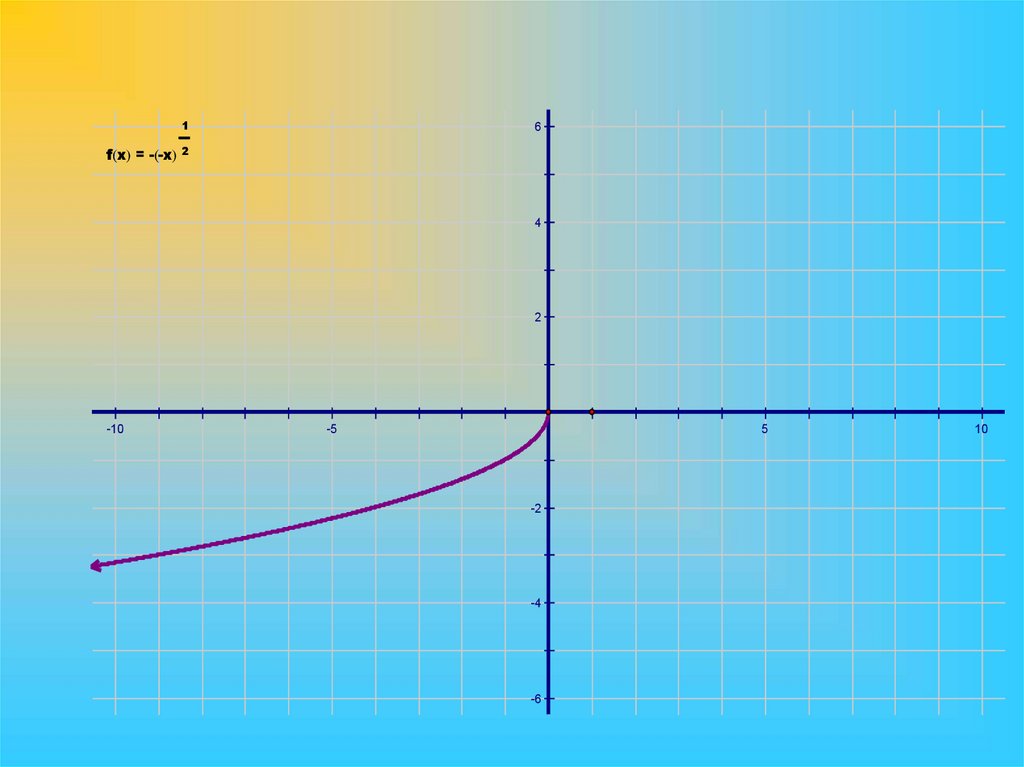



 Математика
Математика








