Похожие презентации:
Функции. Основные характеристики функции. Чётность функции
1. ФУНКЦИИ
2. 3. Основные характеристики функции Чётность функции
• Функция f(x) четная, если x Xсправедливо равенство f ( x) f ( x)
• График четной функции симметричен
относительно оси ОУ.
y
f ( x) x
2
f ( x) ( x) x f ( x )
2
2
0
x
3.
• Функция f(x) нечетная, если x Xсправедливо равенство f ( x) f ( x)
• График нечетной функции симметричен
относительно начало координат (0;0)
y
f ( x) x
y = x3
3
f ( x) ( x) 3 x 3 f ( x)
0
x
4.
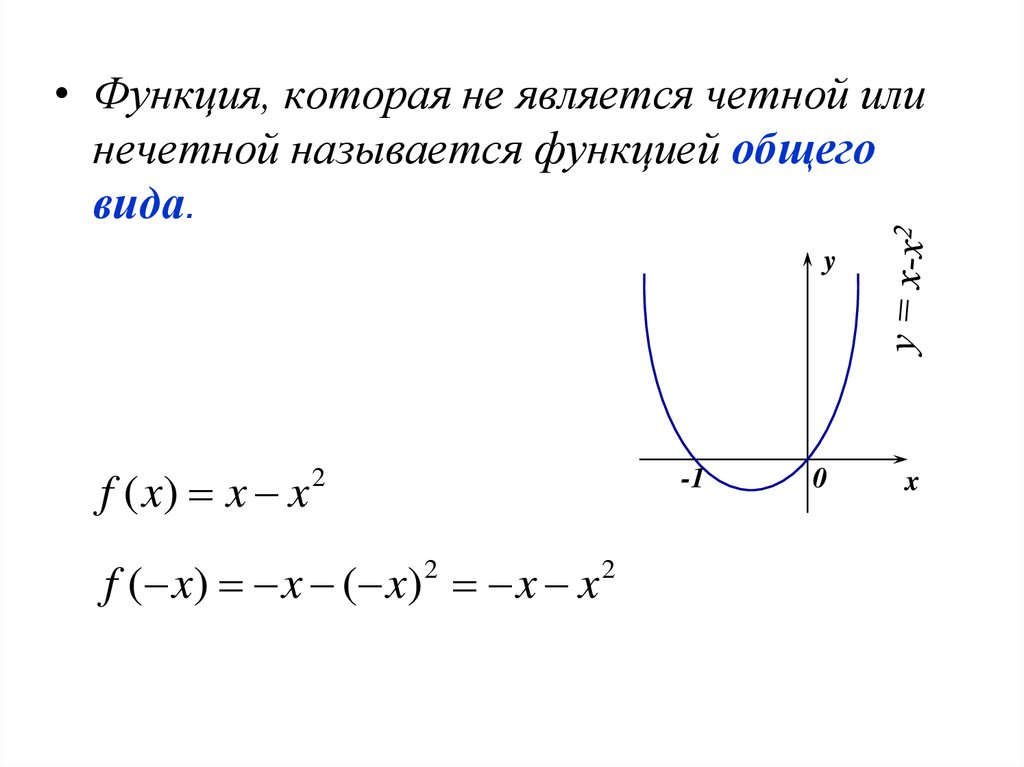
• Функция, которая не является четной илинечетной называется функцией общего
вида.
y
f ( x) x x
-1
2
f ( x) x ( x) x x
2
2
0
x
5.
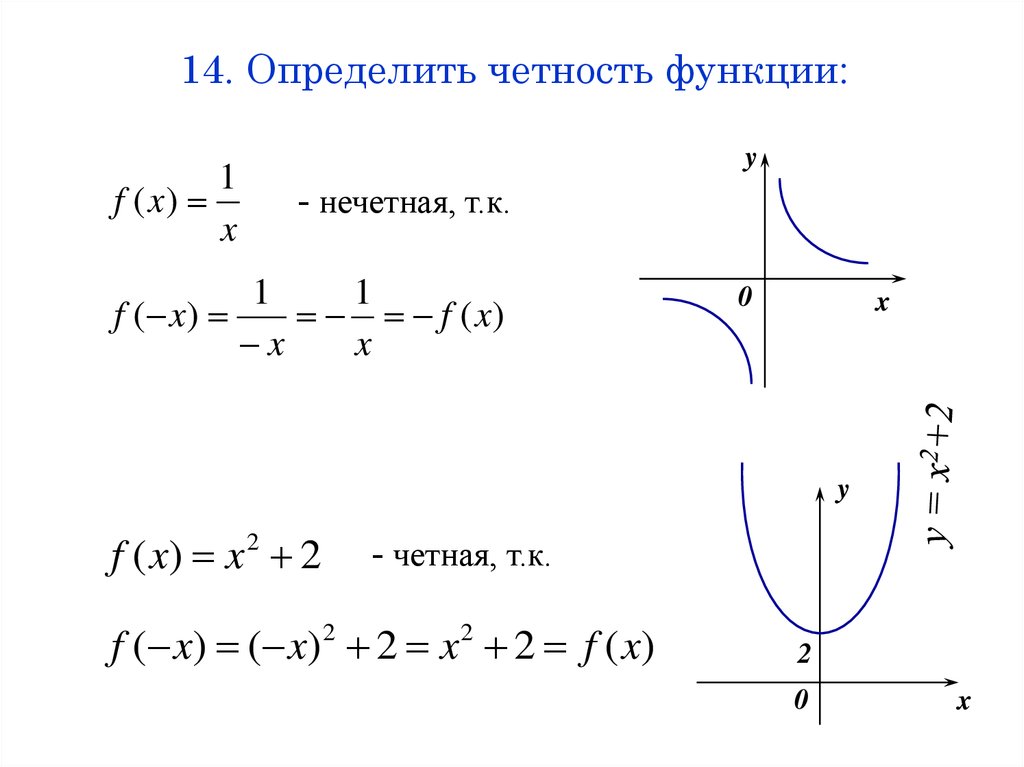
14. Определить четность функции:1
f ( x)
x
y
- нечетная, т.к.
1
1
f ( x)
f ( x)
x
x
0
x
y
f ( x) x 2 2
- четная, т.к.
f ( x ) ( x) 2 2 x 2 2 f ( x)
2
0
x
6.
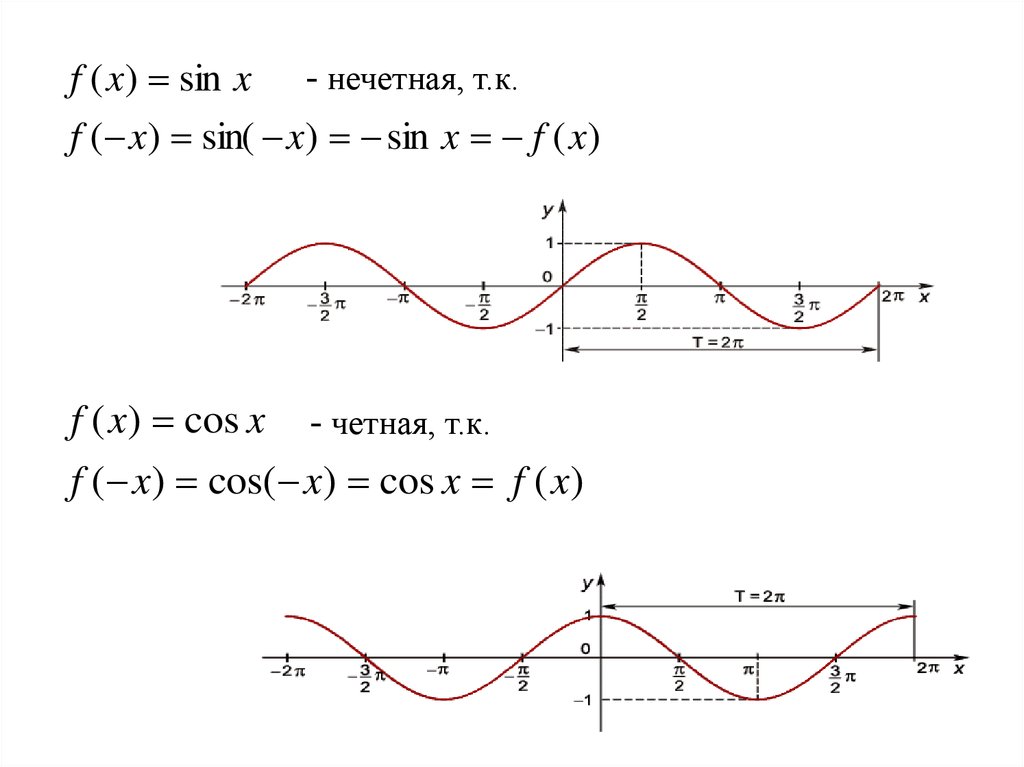
f ( x) sin x - нечетная, т.к.f ( x) sin( x) sin x f ( x)
f ( x) cos x - четная, т.к.
f ( x) cos( x) cos x f ( x)
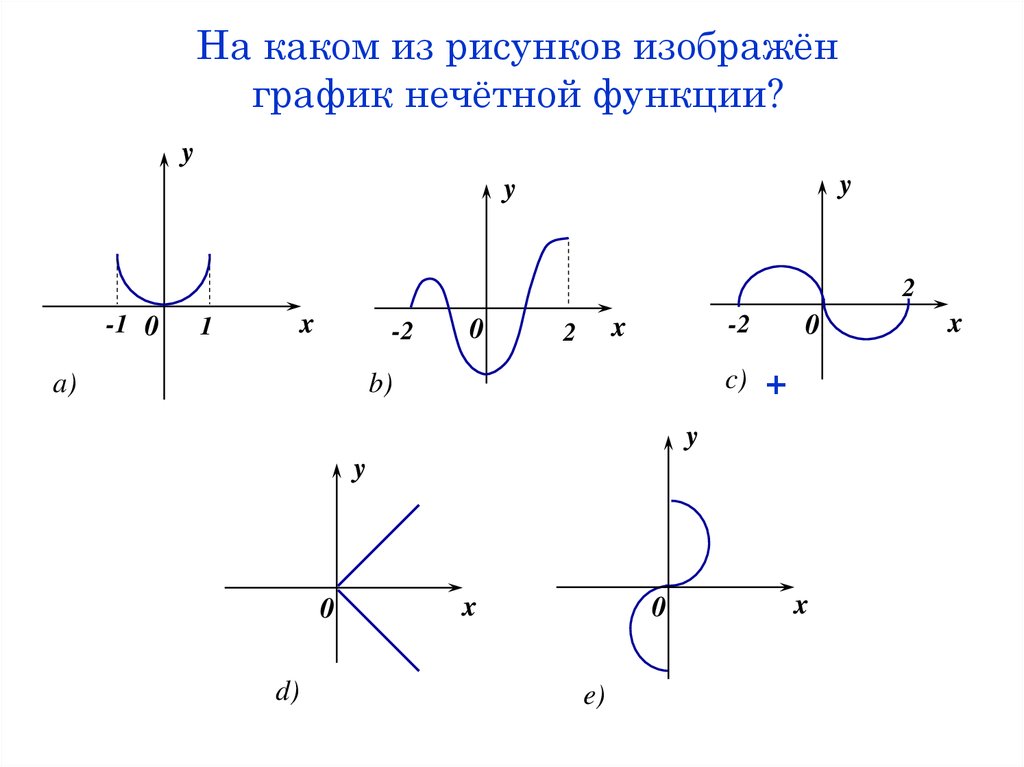
7. На каком из рисунков изображён график нечётной функции?
yy
y
2
-1 0
x
1
-2
a)
0
0
-2
x
2
c)
b)
+
y
y
0
d)
x
0
e)
x
x
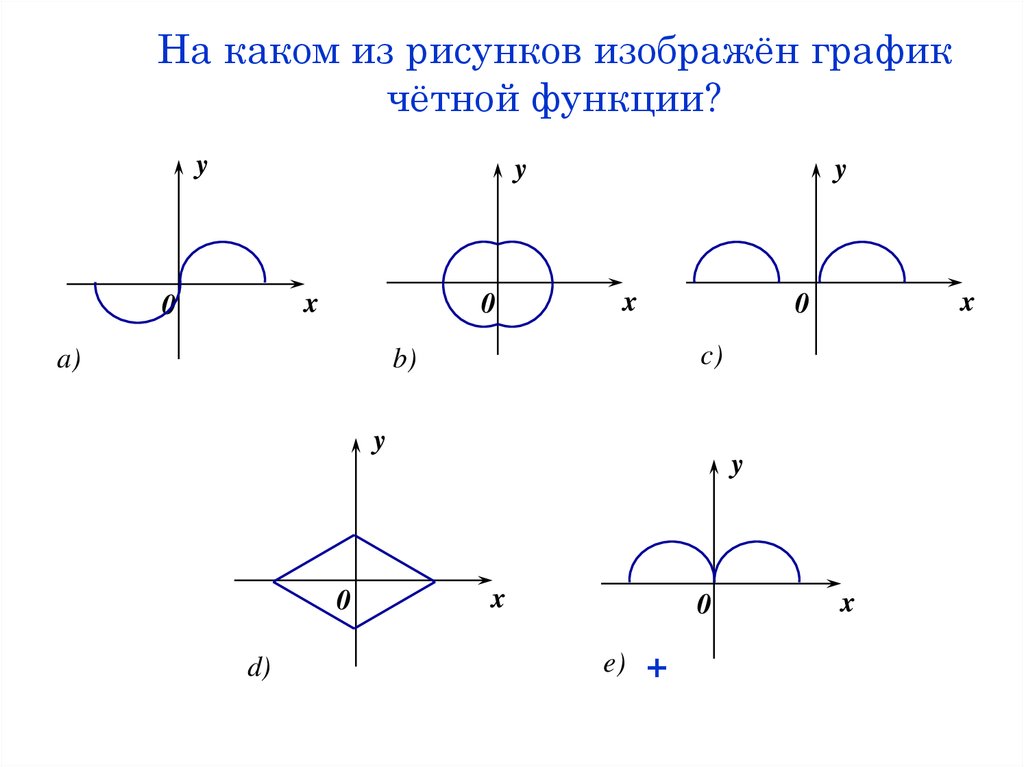
8. На каком из рисунков изображён график чётной функции?
yy
x
0
0
a)
y
x
c)
b)
y
0
d)
x
0
y
x
0
e)
+
x
9. Монотонность
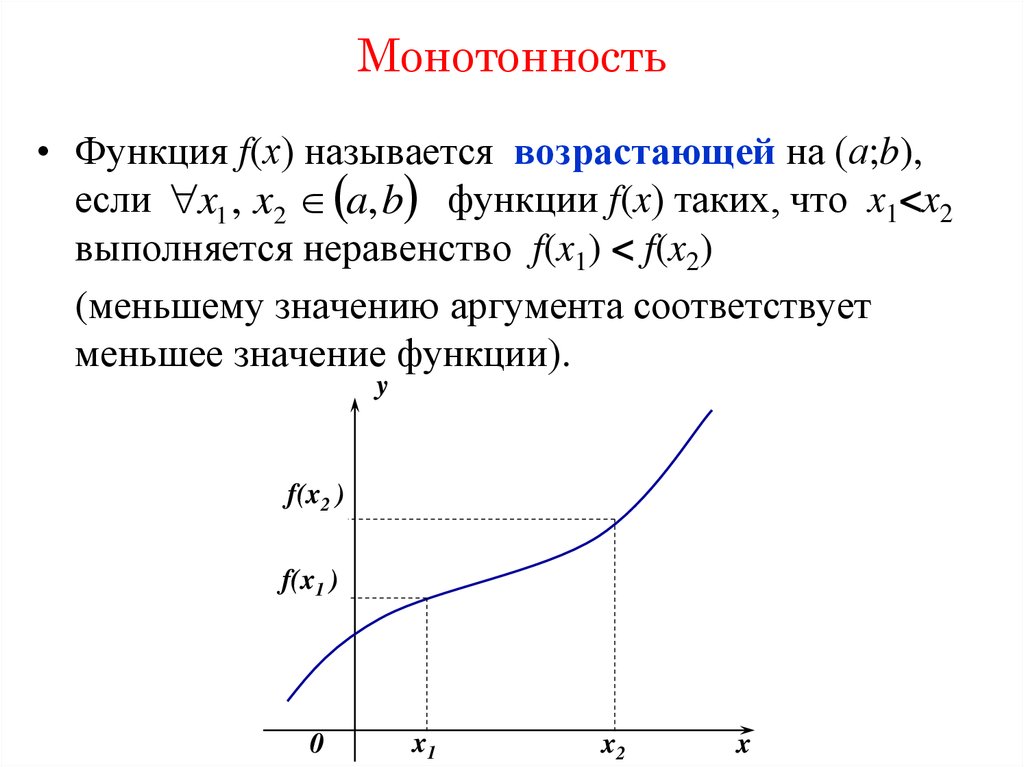
• Функция f(х) называется возрастающей на (а;b),если x1 , x2 a, b функции f(x) таких, что x1<x2
выполняется неравенство f(x1) < f(x2)
(меньшему значению аргумента соответствует
меньшее значение функции).
y
f(x2 )
f(x1 )
0
x1
x2
x
10.
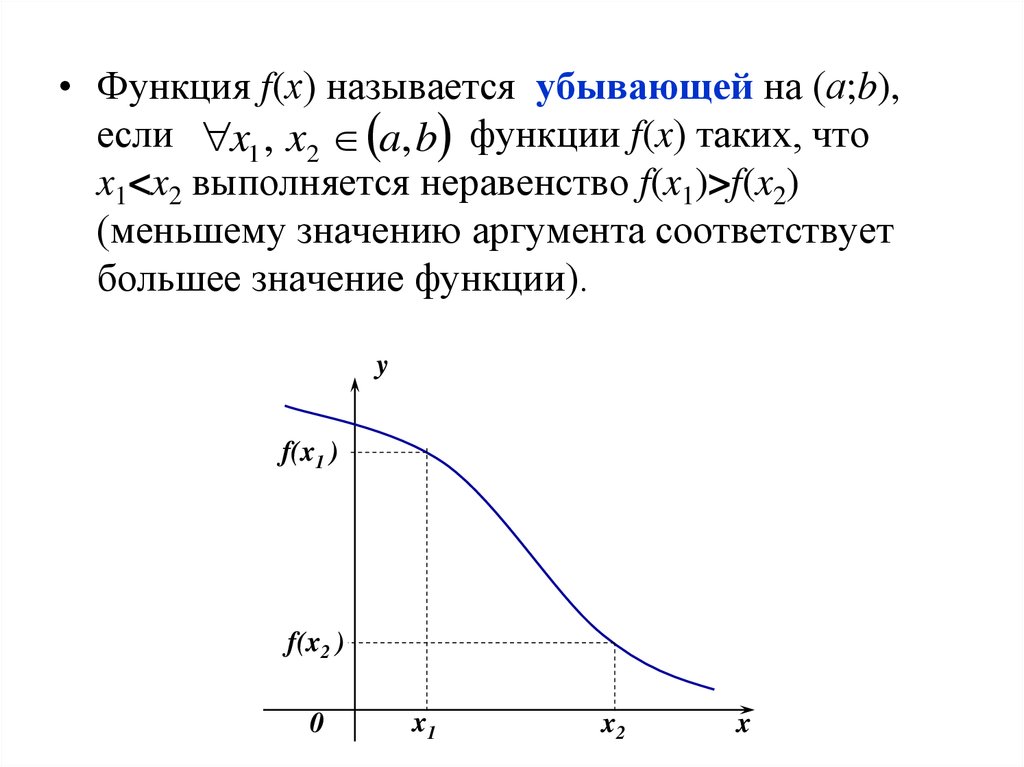
• Функция f(х) называется убывающей на (а;b),если x1 , x2 a, b функции f(x) таких, что
x1<x2 выполняется неравенство f(x1)>f(x2)
(меньшему значению аргумента соответствует
большее значение функции).
y
f(x1 )
f(x2 )
0
x1
x2
x
11.
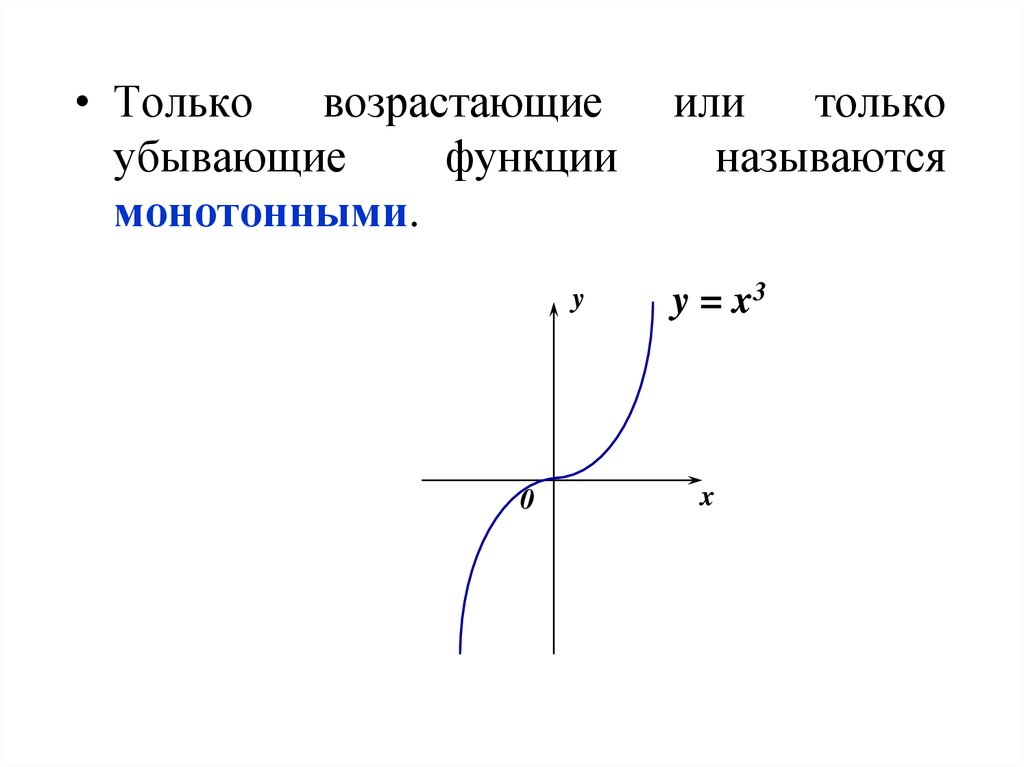
• Тольковозрастающие
убывающие
функции
монотонными.
y
0
или
только
называются
y = x3
x
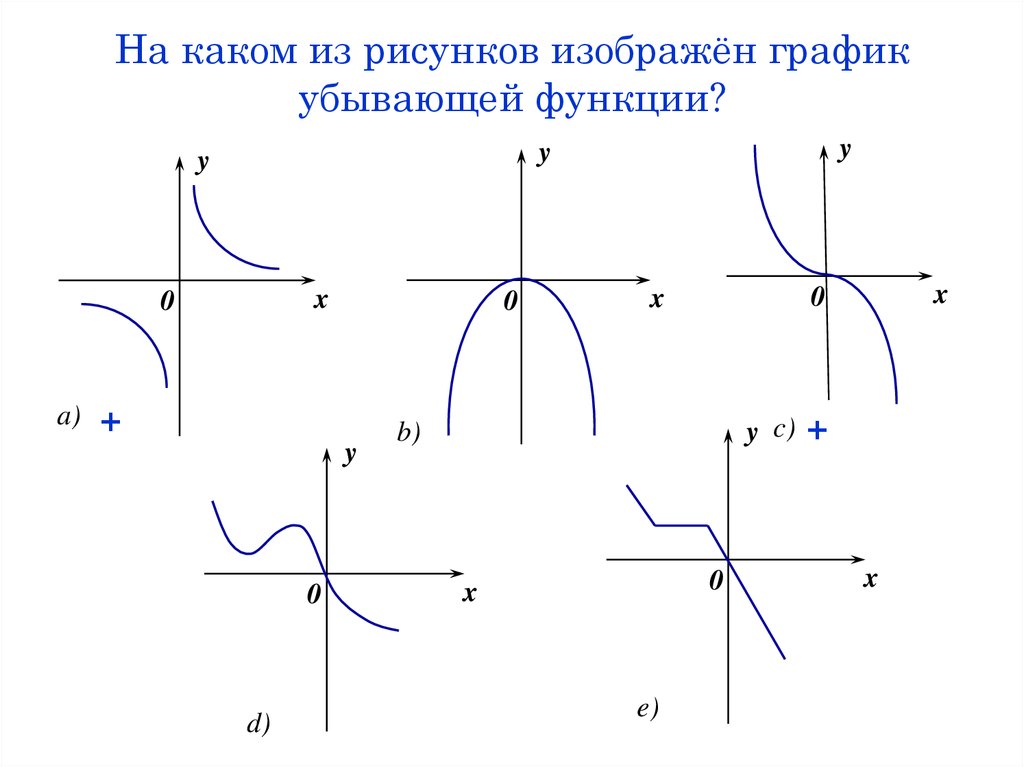
12. На каком из рисунков изображён график убывающей функции?
x0
a)
y
y
y
+
0
y
0
d)
y c)
b)
0
x
e)
x
0
x
+
x
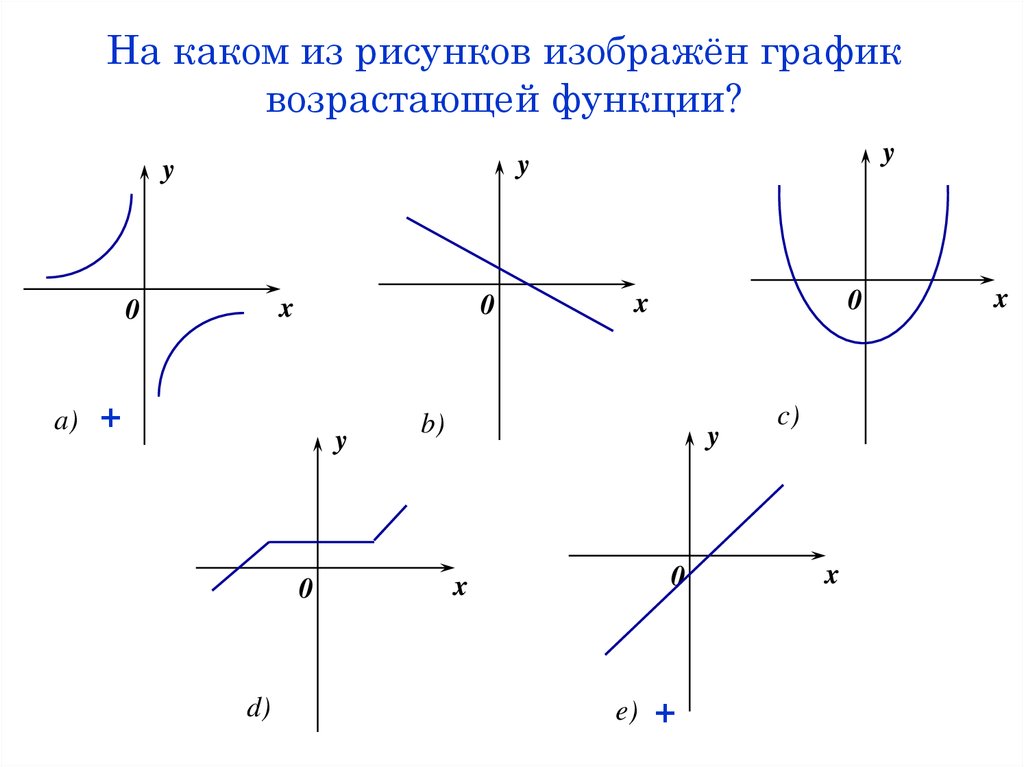
13. На каком из рисунков изображён график возрастающей функции?
0x
0
a)
y
y
y
+
y
0
d)
0
x
b)
y
0
x
e)
+
c)
x
x
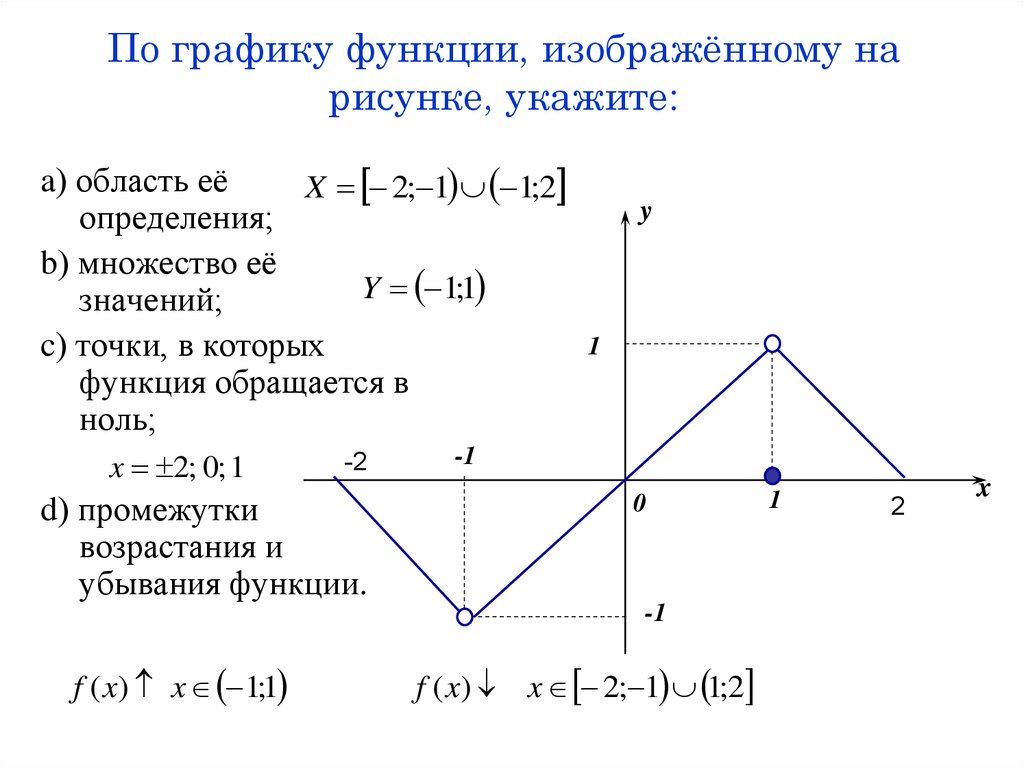
14. По графику функции, изображённому на рисунке, укажите:
a) область еёX 2; 1 1;2
определения;
b) множество её
Y 1;1
значений;
c) точки, в которых
функция обращается в
ноль;
x 2; 0; 1
-2
d) промежутки
возрастания и
убывания функции.
y
1
-1
0
-1
f ( x) x 1;1
f ( x) x 2; 1 1;2
1
2
x
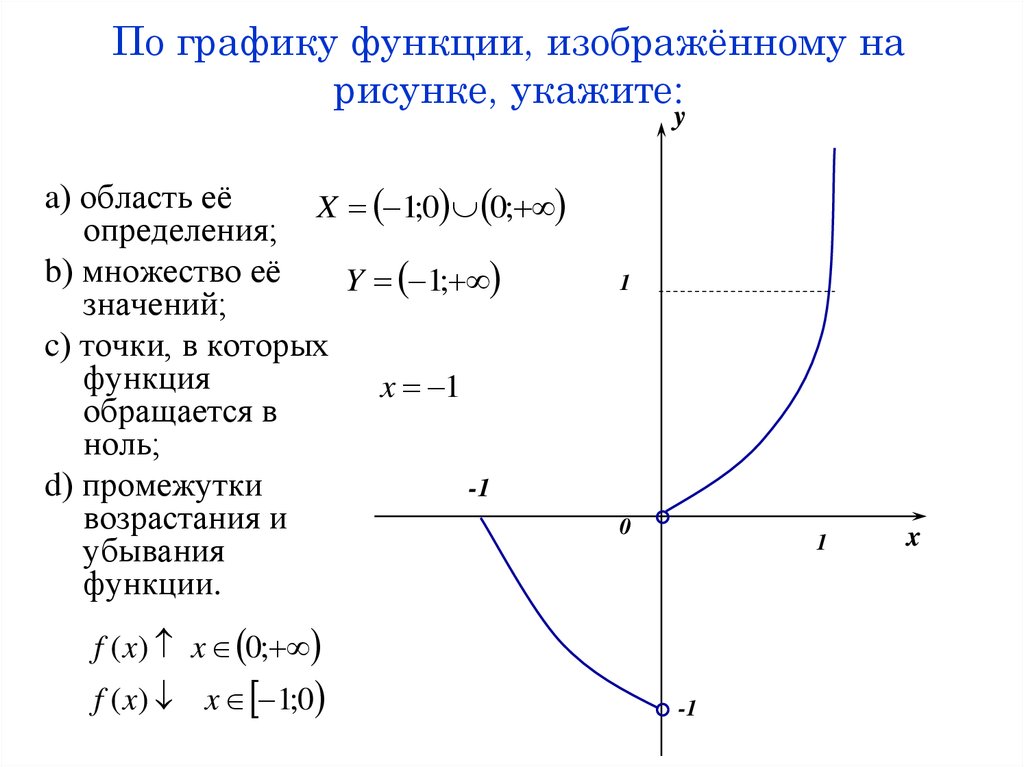
15. По графику функции, изображённому на рисунке, укажите:
ya) область её
X 1;0 0;
определения;
b) множество её
Y 1;
значений;
c) точки, в которых
функция
x 1
обращается в
ноль;
d) промежутки
-1
возрастания и
убывания
функции.
1
0
1
f ( x) x 0;
f ( x) x 1;0
-1
x
16. По графику функции, изображённому на рисунке, укажите:
ya) область её
X 1,5;1,5
определения;
1
b) множество её
X 1; 0,5 0,5;1
значений;
c) точки, в которых
0,5
функция
обращается в
-0,5
-1,5
ноль;
(нет)
0
d) промежутки
возрастания и
убывания
функции.
f ( x) x 0,5;0,5
0,5
-0,5
-1
1,5
x
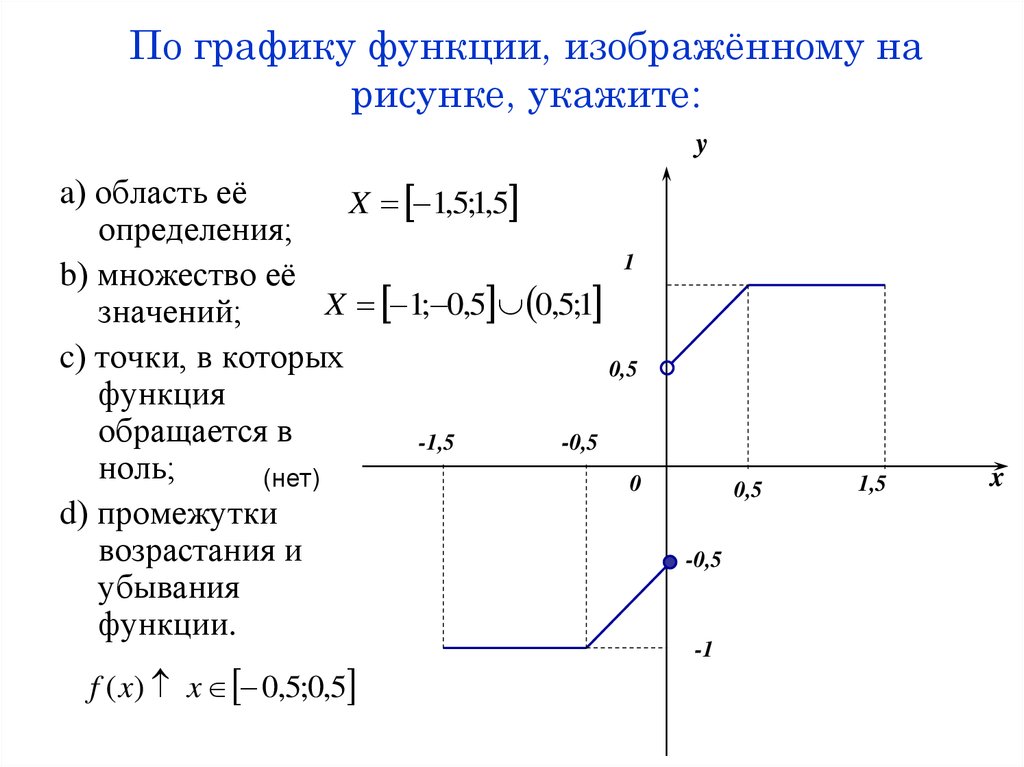
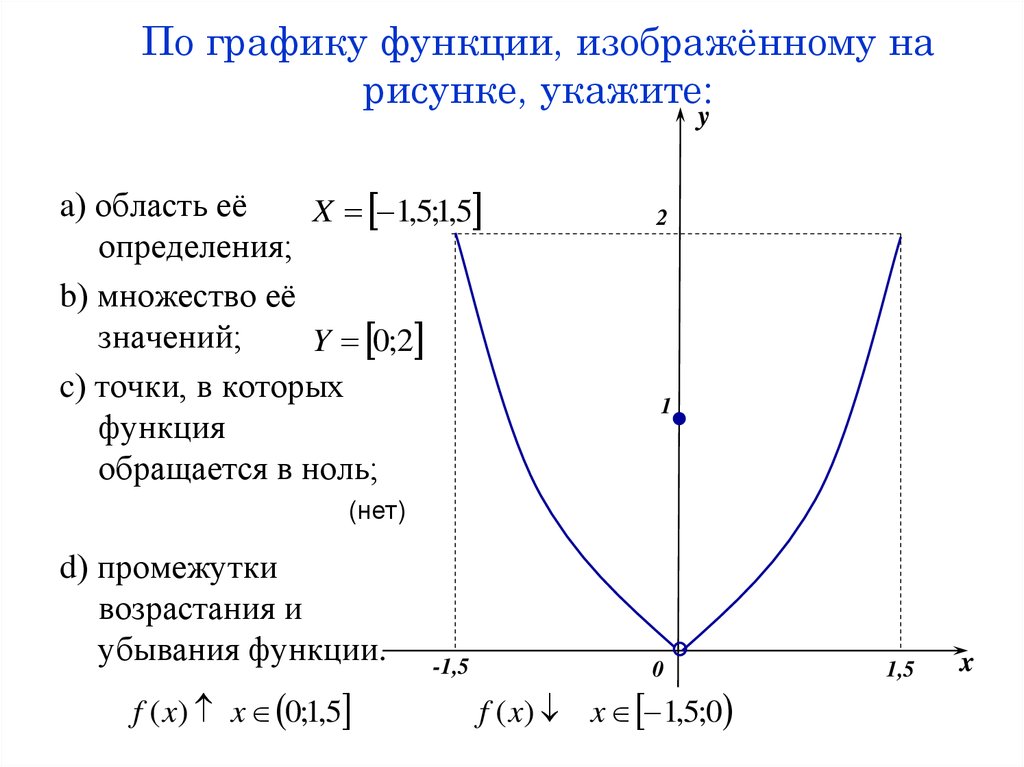
17. По графику функции, изображённому на рисунке, укажите:
ya) область её
X 1,5;1,5
определения;
b) множество её
значений;
Y 0;2
c) точки, в которых
функция
обращается в ноль;
2
1
(нет)
d) промежутки
возрастания и
убывания функции.
f ( x) x 0;1,5
-1,5
0
f ( x) x 1,5;0
1,5
x
18.
Периодические функции.• Функция f(x) называется периодической, если
существует такое число Т≠0 (называемое
периодом), что в каждой точке области
определения функции f(x) выполняется условие
f(x+T)=f(x)
Например: y=sinx и y=tanx - периодические
Tsin x 2
Ttan x
sin( x 2 ) sin x
tan( x ) tan x
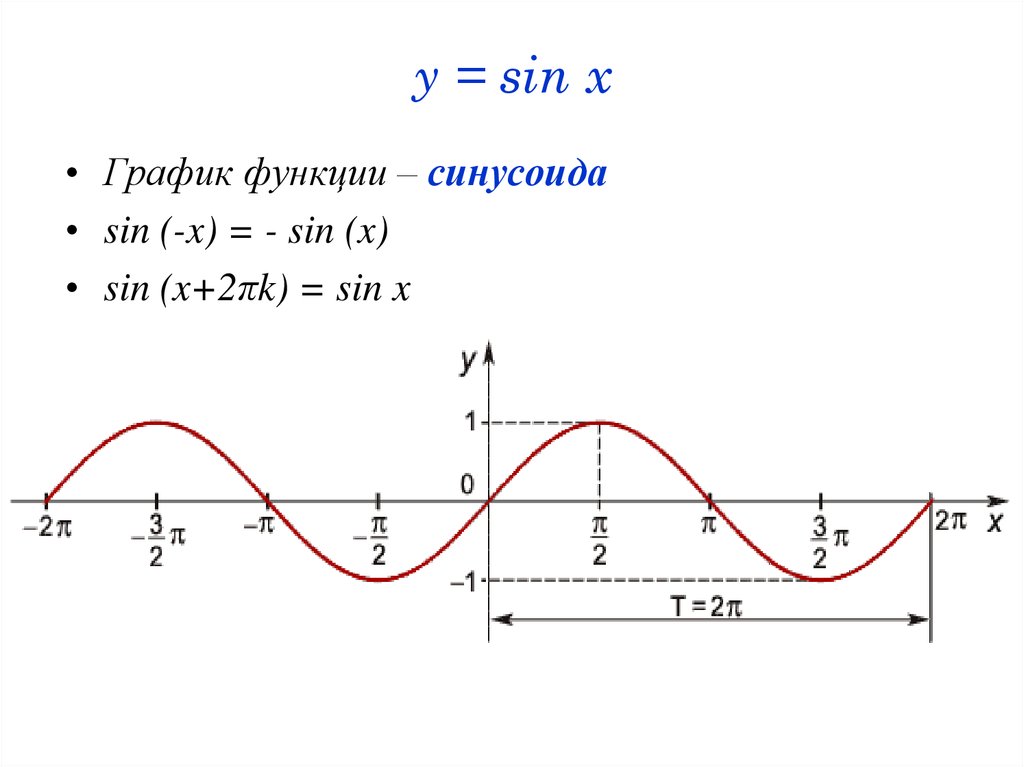
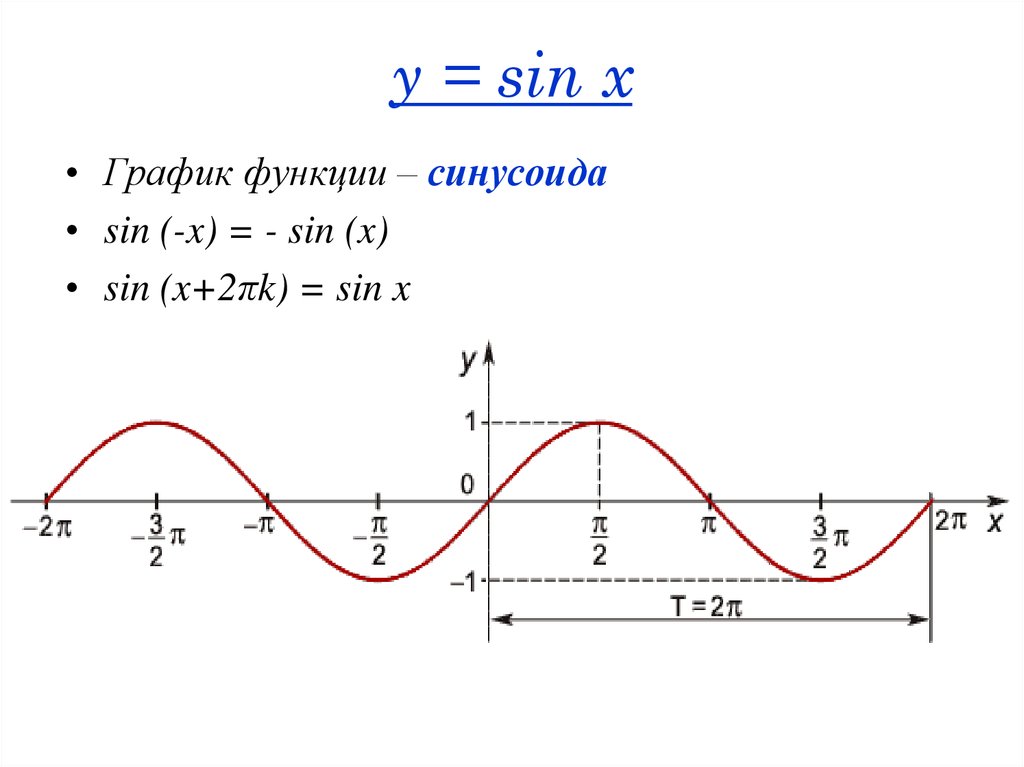
19. y = sin x
• График функции – синусоида• sin (-x) = - sin (x)
• sin (x+2πk) = sin x
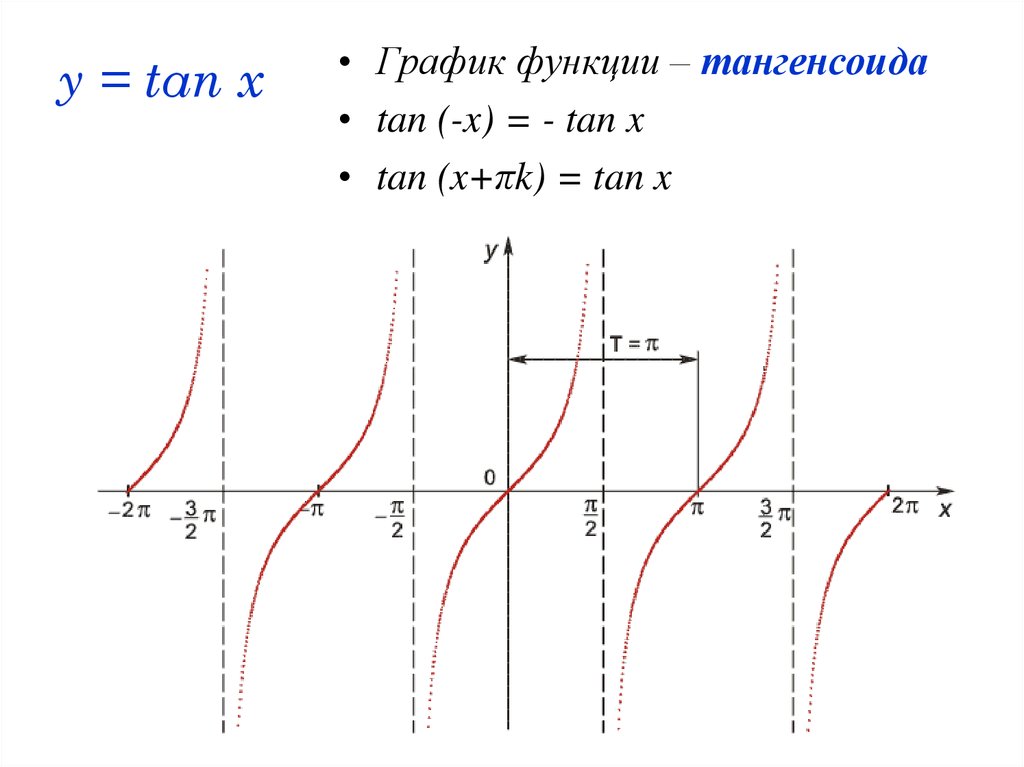
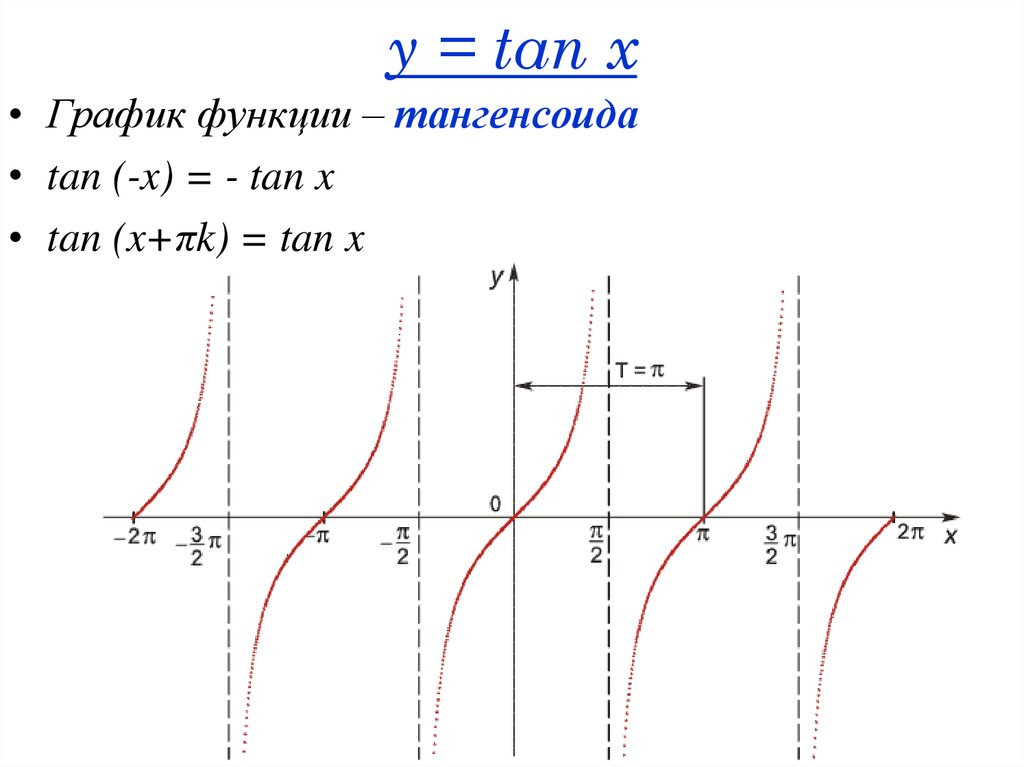
20. y = tan x
• График функции – тангенсоида• tan (-x) = - tan x
• tan (x+πk) = tan x
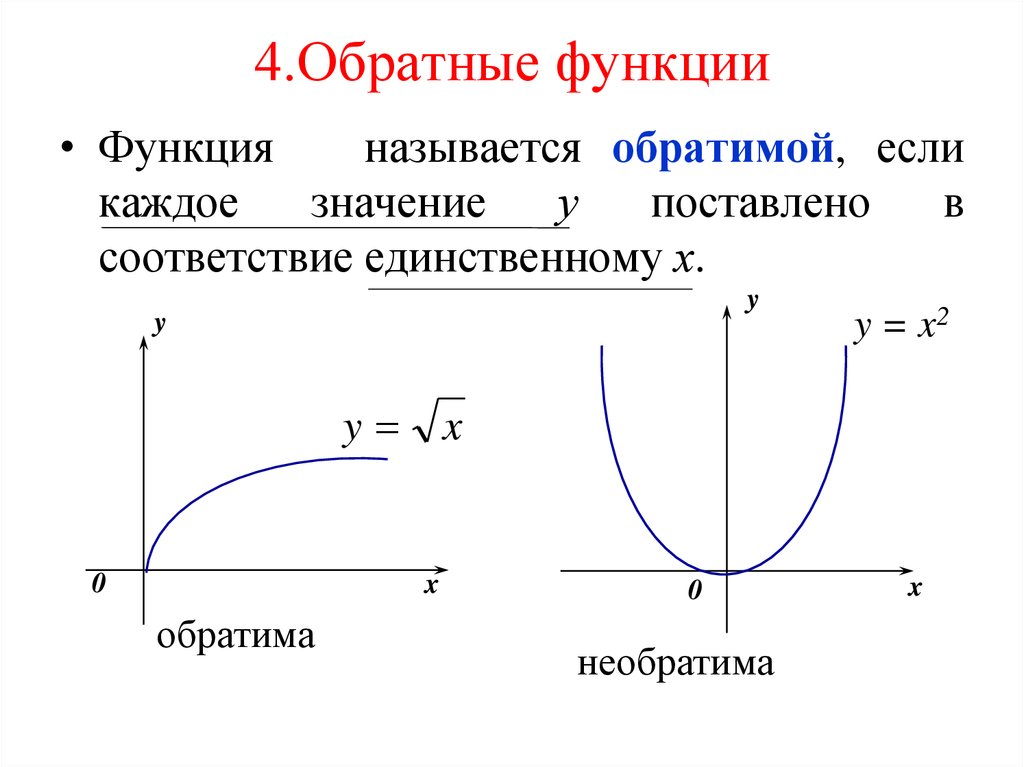
21. 4.Обратные функции
• Функцияназывается обратимой, если
каждое
значение
у
поставлено
в
соответствие единственному х.
y
y
y
0
x
x
обратима
y = x2
0
необратима
x
22.
• Пусть функция f : X Y обратима. Тогда намножестве У определена функция f 1 : Y X ,
которая каждому y Y ставит в соответствие
единственный x X
X
f
x
Y
y
f-1
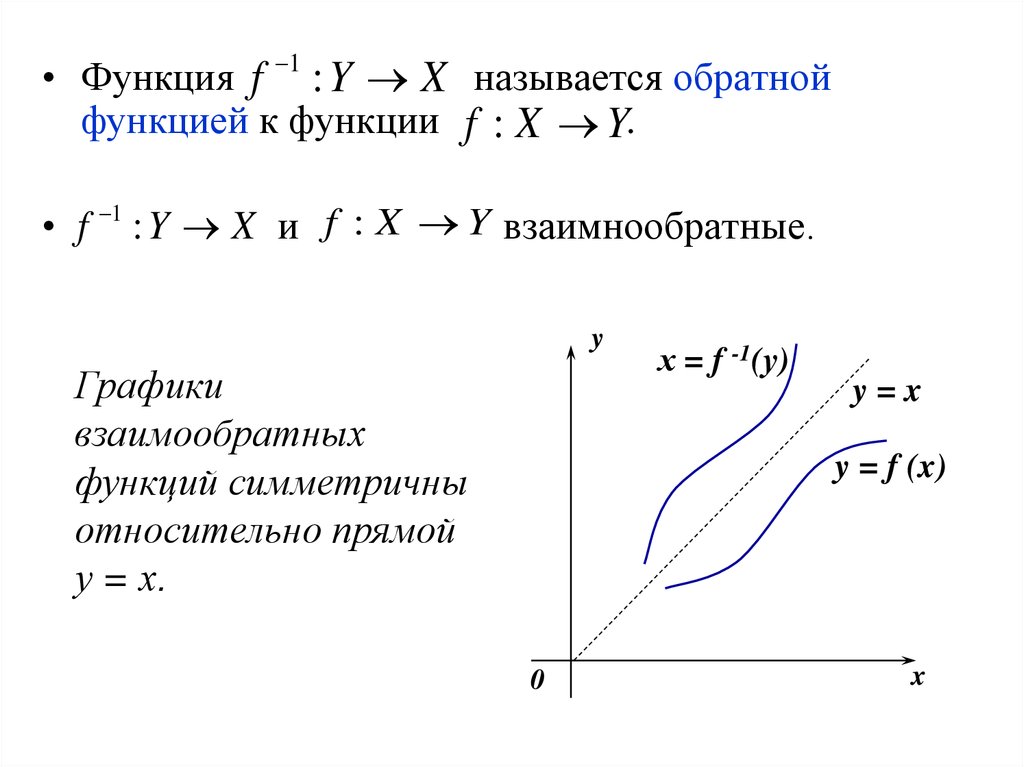
23.
1• Функция f : Y X называется обратной
функцией к функции f : X Y.
• f
1
: Y X и f : X Y взаимнообратные.
y
Графики
взаимообратных
функций симметричны
относительно прямой
у = х.
х = f -1(у)
y=x
y = f (x)
0
x
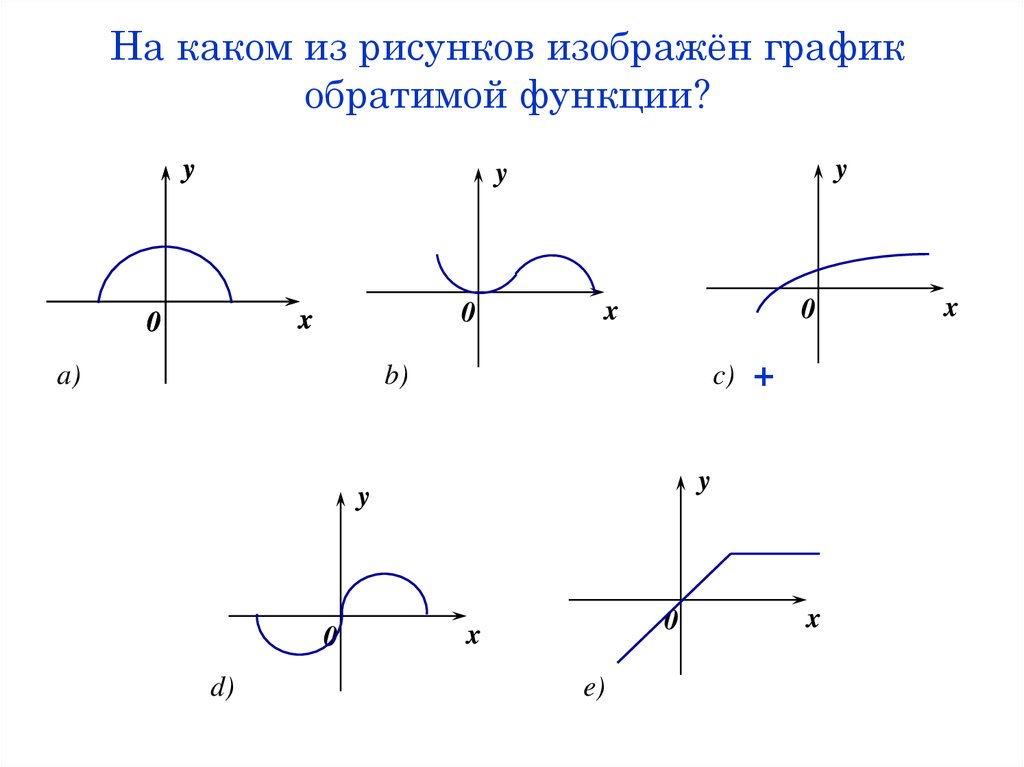
24. На каком из рисунков изображён график обратимой функции?
yy
y
0
x
0
0
x
b)
a)
c)
y
y
0
d)
+
0
x
e)
x
x
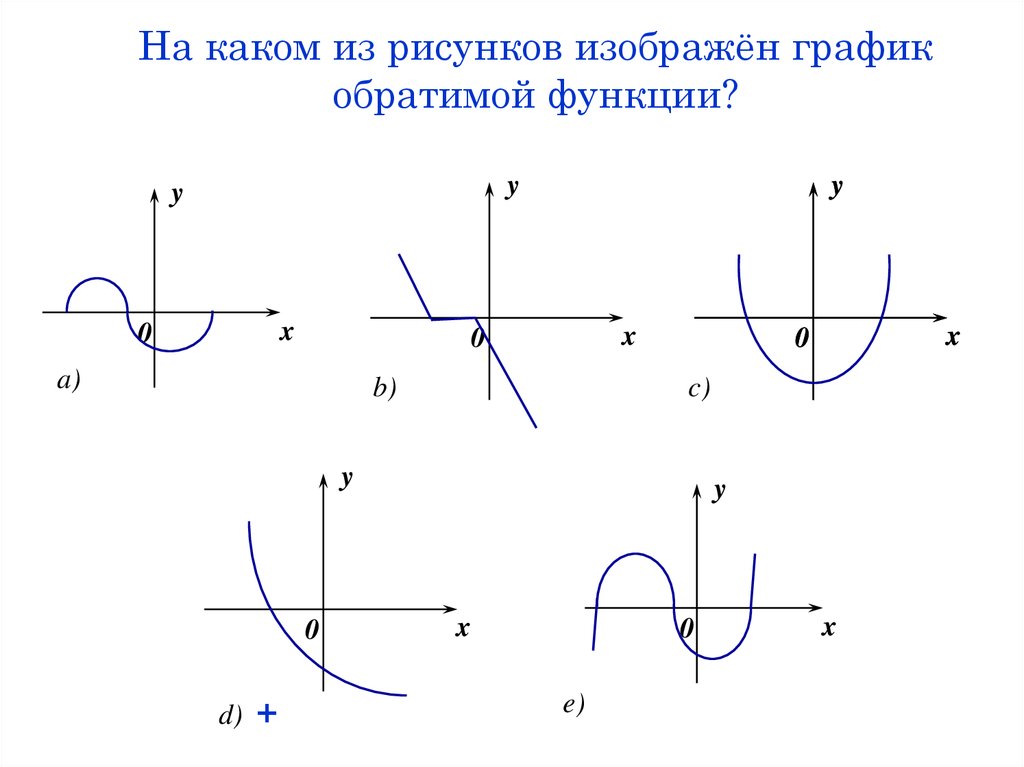
25. На каком из рисунков изображён график обратимой функции?
yy
x
0
y
x
0
a)
b)
c)
y
0
d)
+
x
0
y
x
0
e)
x
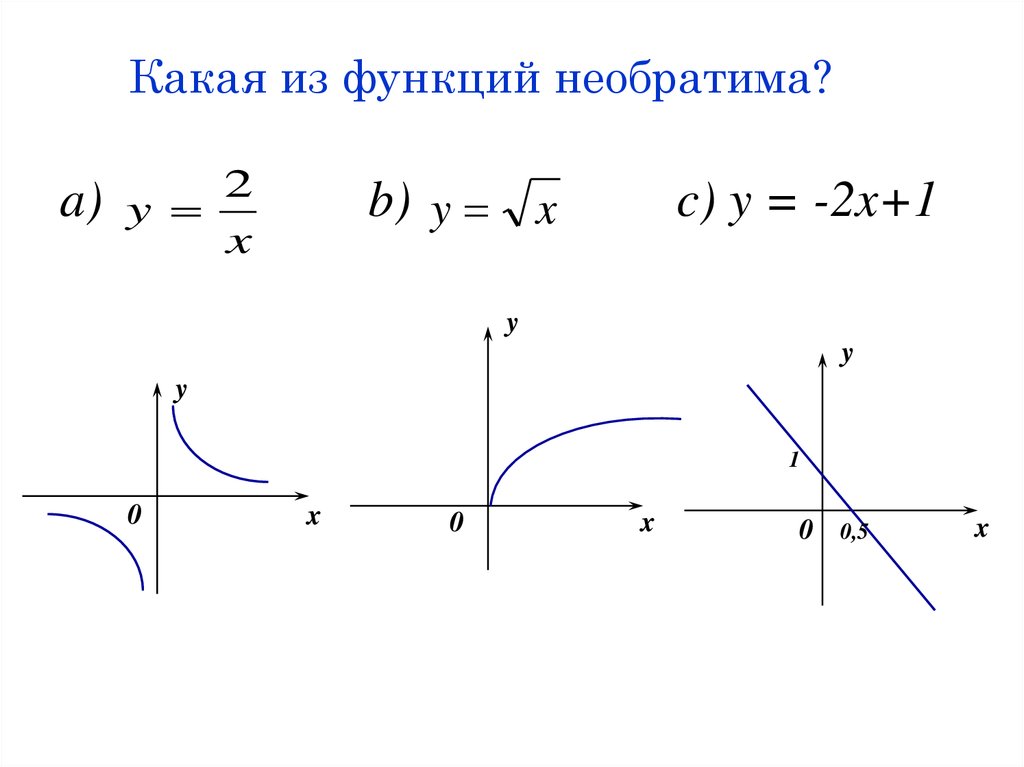
26. Какая из функций необратима?
a)2
y
x
b) y x
c) y = -2x+1
y
y
y
1
0
x
0
x
0
0,5
x
27. Какая из функций необратима?
d) y = x3e) y = (x-1)2
y
0
f) y = x2
y
y
x
0
1
+
x
0
x
+
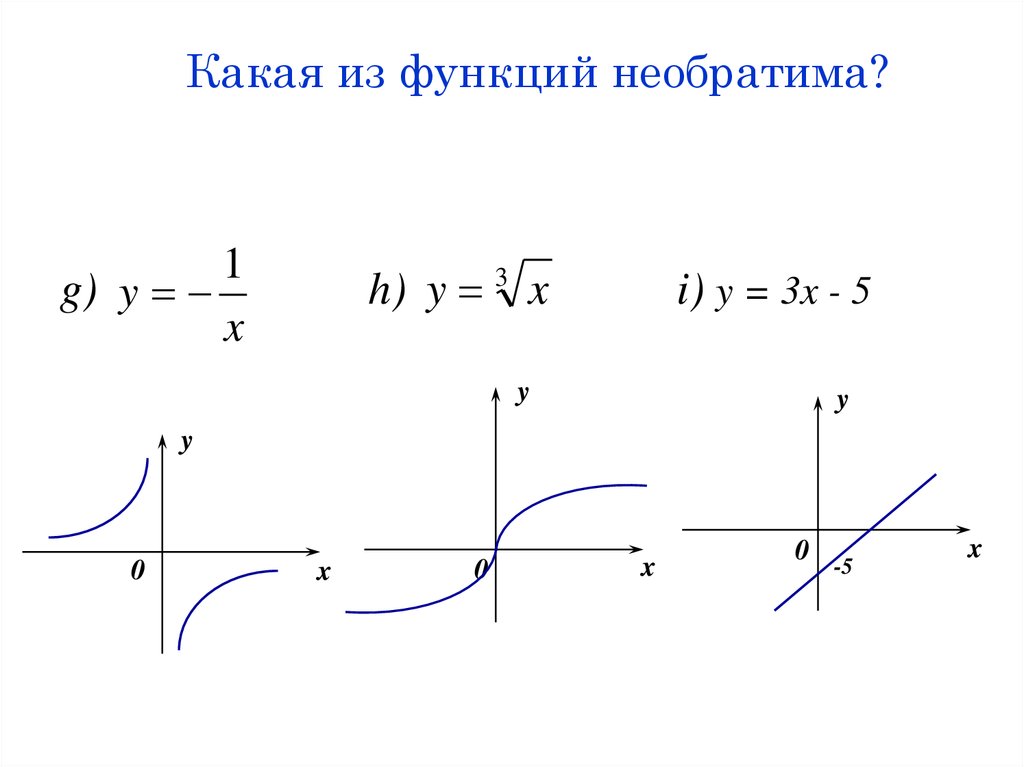
28. Какая из функций необратима?
1g) y
x
h) y 3 x
i) y = 3x - 5
y
y
y
0
x
0
x
0
-5
x
29.
15. Найти обратную функцию для функции:f ( x) 2 x 1
y 2x 1
y 2x 1
2x y 1
y 1
x
2
или
x 1
y
2
у
y x
y
0
х
x 1
2
30.
16. Найти обратную функцию для функции:f ( x) x , x 0;
2
y x
2
y x2
x y
x
y
у
mak kak
x 0
y x
y
или
y x , x 0;
0
х
x
31. 5. Основные элементарные функции
Степенная функция.
Показательная функция
Логарифмическая функция
Тригонометрические функции
Обратные тригонометрические функции
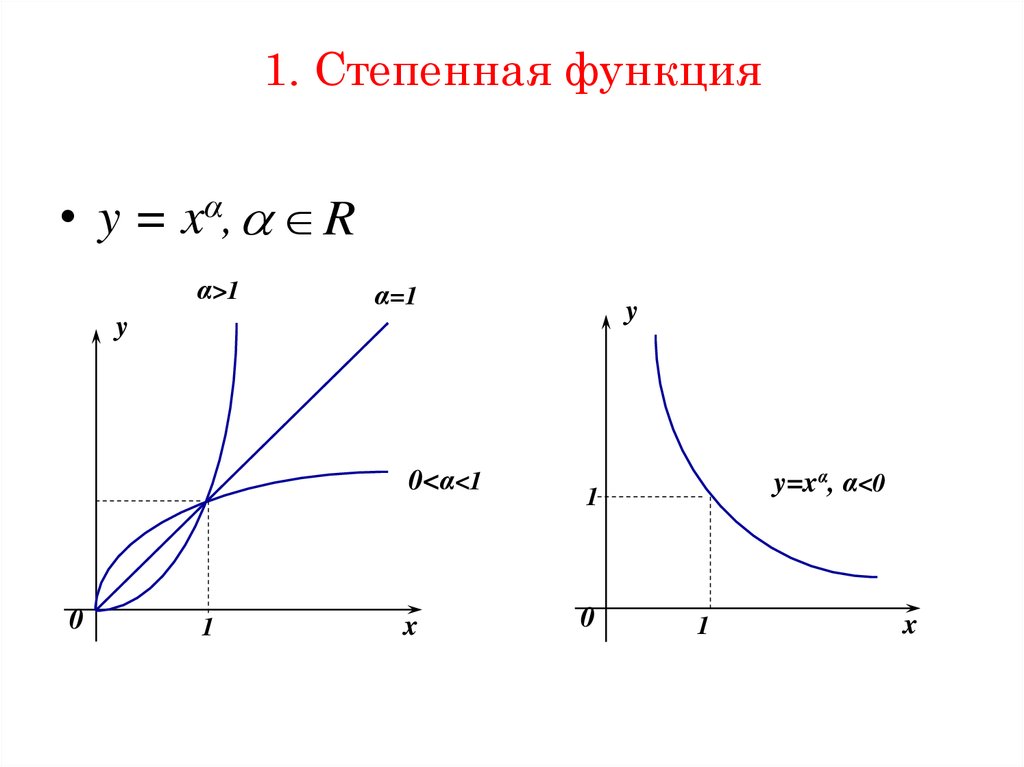
32. 1. Степенная функция
• y = xα, Rα>1
α=1
y
y
0<α<1
0
1
x
y=xα, α<0
1
0
1
x
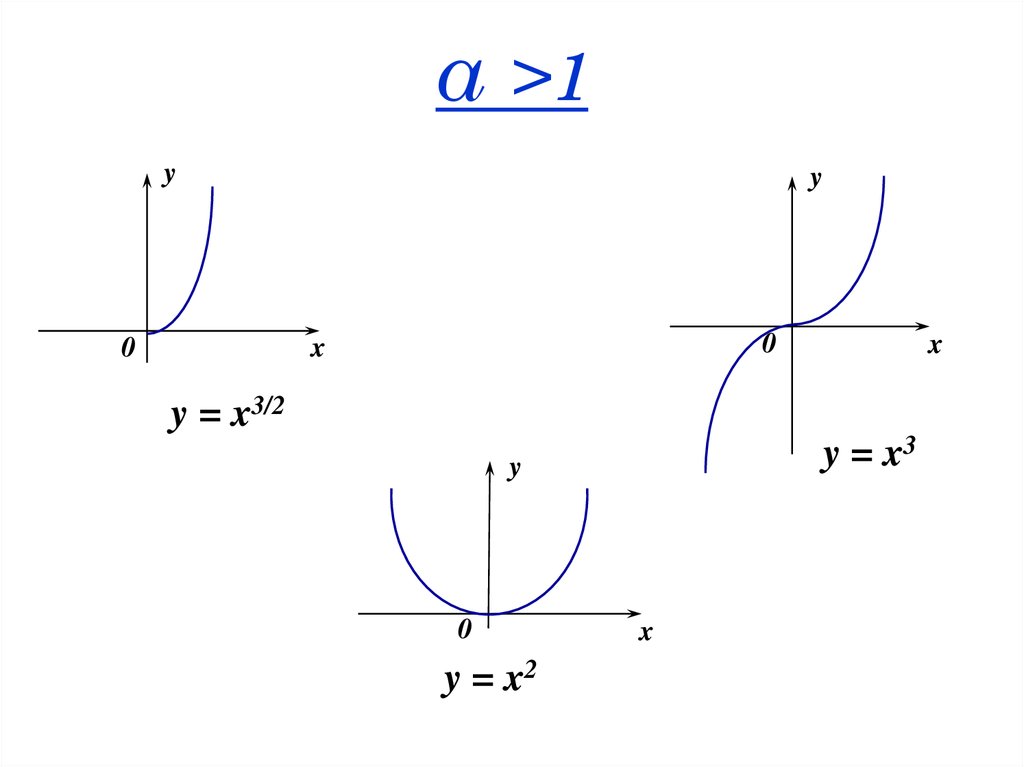
33. α >1
α >1y
0
y
0
x
x
y = x3/2
y = x3
y
0
y = x2
x
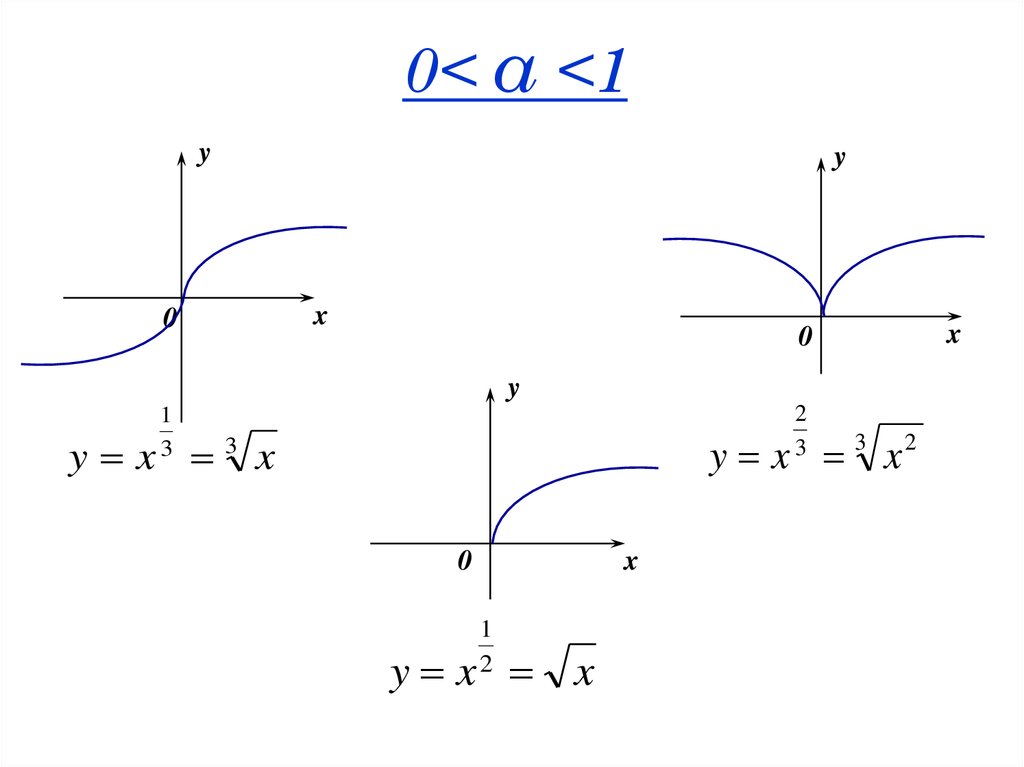
34. 0< α <1
0< α <1y
0
y
x
0
y
2
3
1
3
y x 3 x2
y x 3 x
0
x
1
2
y x x
x
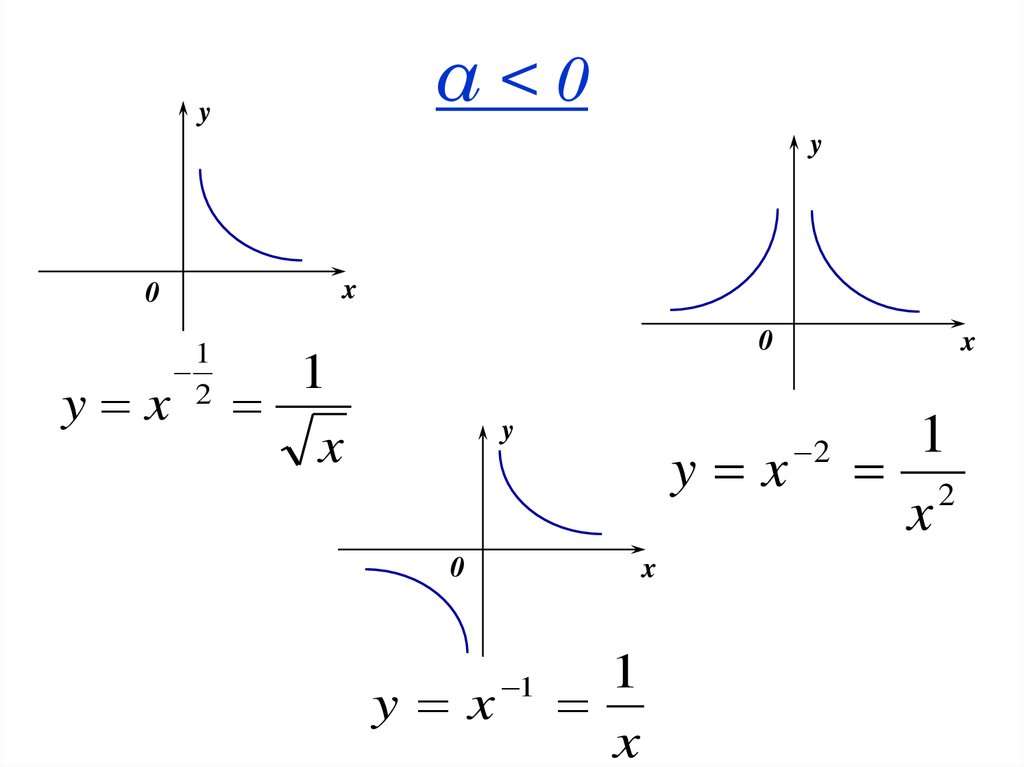
35. α < 0
α<0y
y
x
0
y x
1
2
0
1
x
y
y x
0
y x
x
1
1
x
x
2
1
2
x
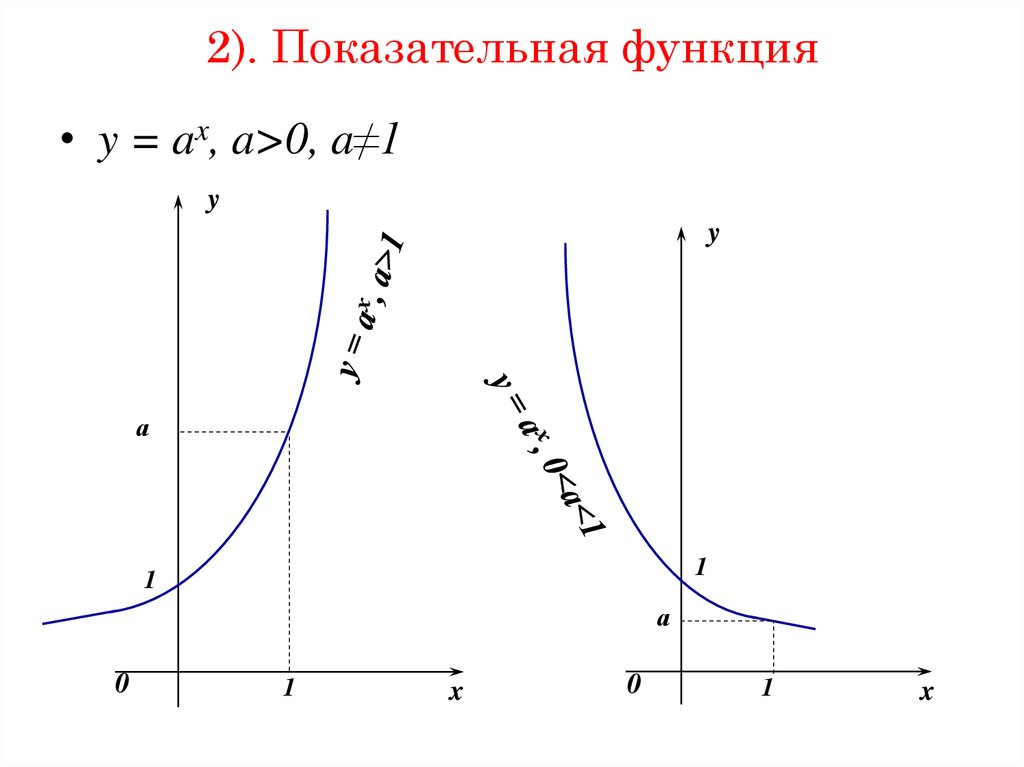
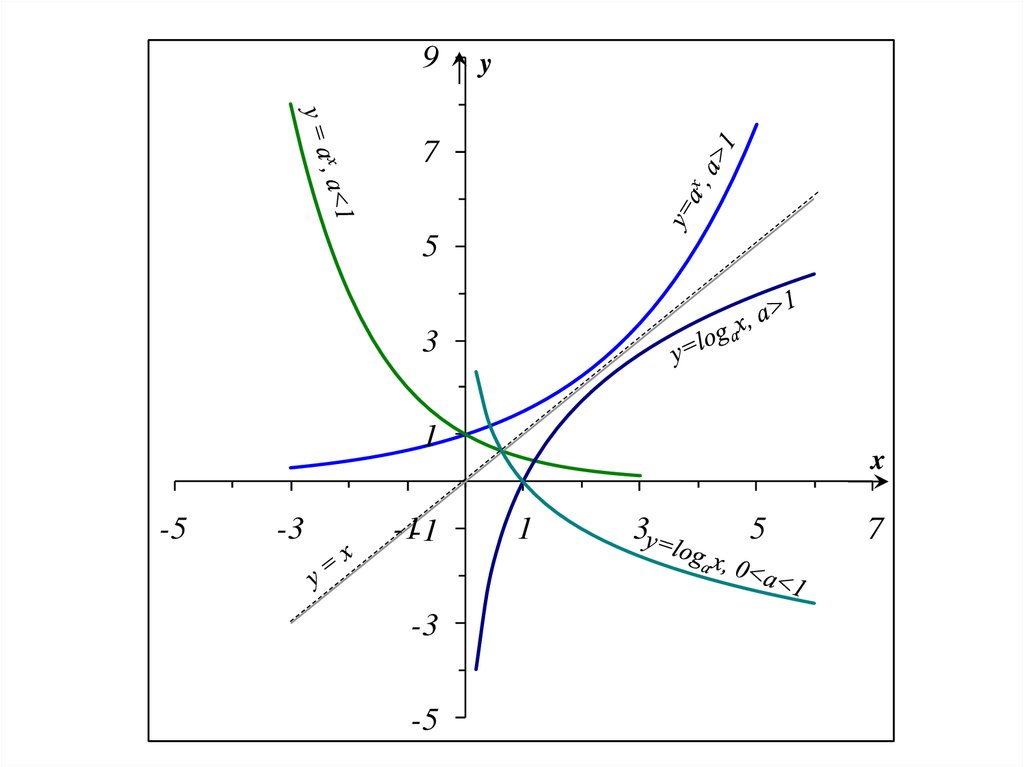
36. 2). Показательная функция
• y = ax, a>0, a≠1y
y
а
1
1
а
0
1
x
0
1
x
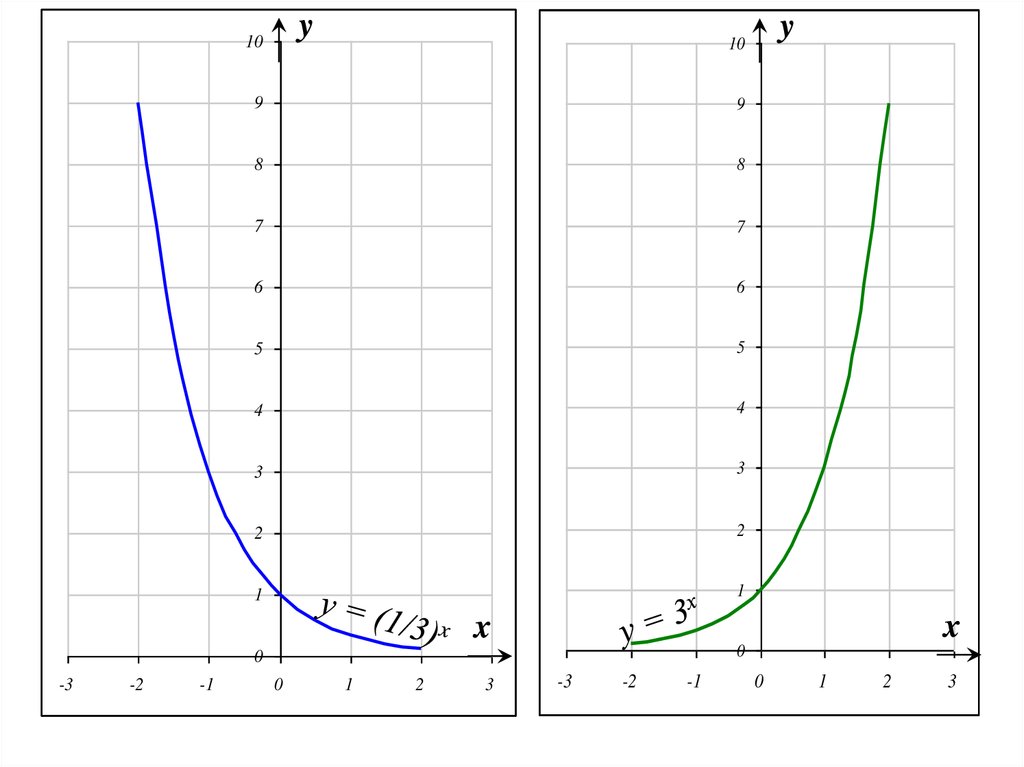
37.
y10
9
9
8
8
7
7
6
6
5
5
4
4
3
3
2
2
1
1
x
x
0
0
-3
-2
-1
0
y
10
1
2
3
-3
-2
-1
0
1
2
3
38.
y4
3
2
1
x
0
-3
-2
-1
0
1
2
3
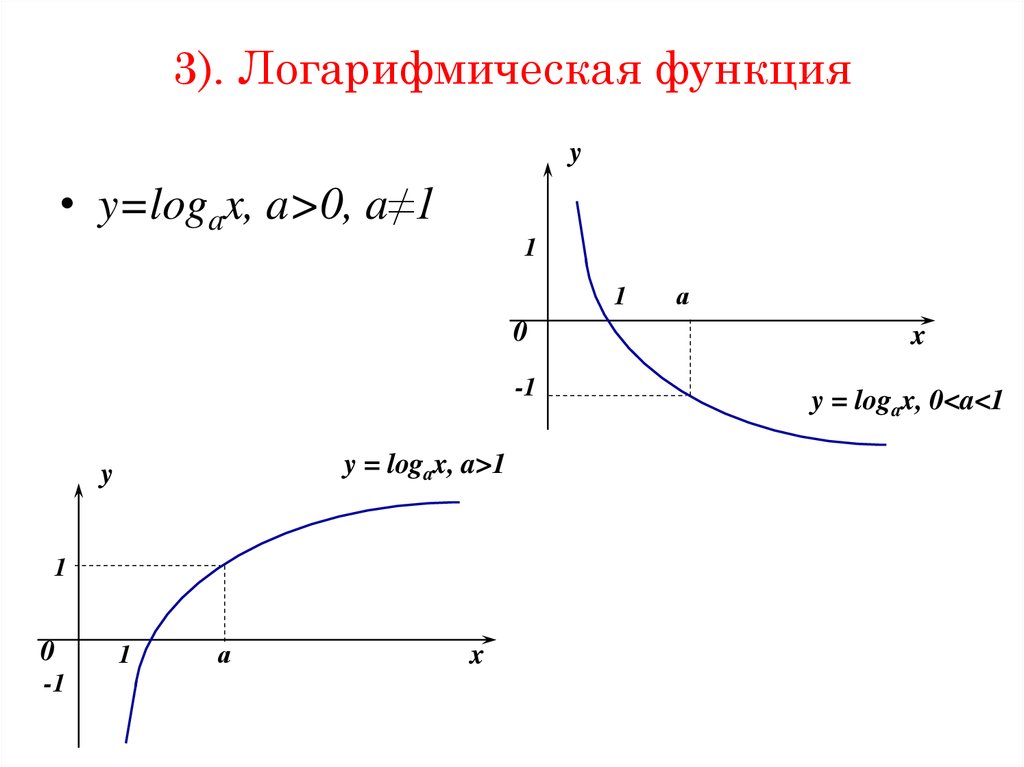
39. 3). Логарифмическая функция
y• y=logax, a>0, a≠1
1
1
0
-1
y = logax, a>1
y
1
0
-1
1
а
x
а
x
y = logax, 0<a<1
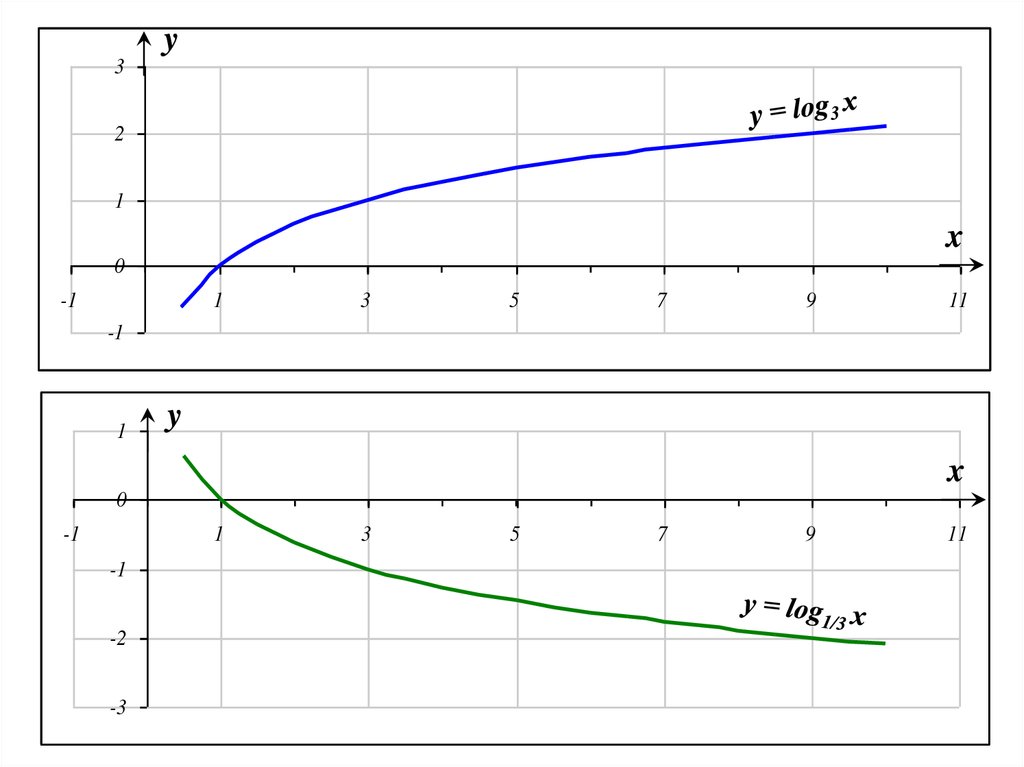
40.
y3
2
1
x
0
-1
1
3
5
7
9
11
-1
1
y
x
0
-1
1
-1
-2
-3
3
5
7
9
11
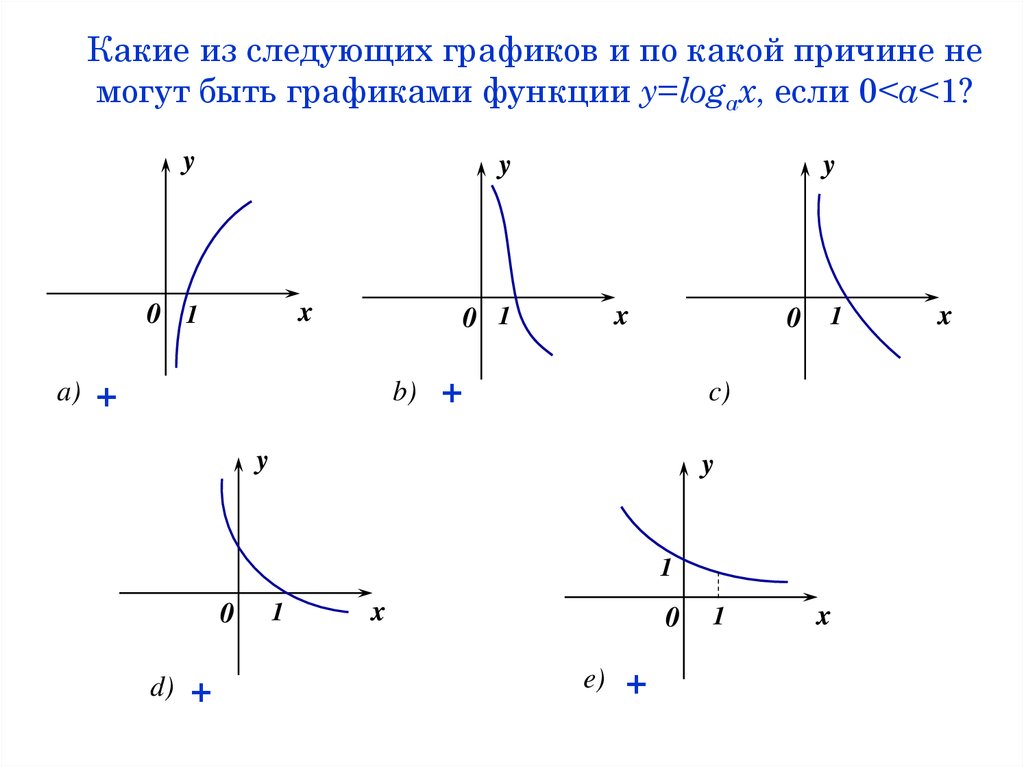
41. Какие из следующих графиков и по какой причине не могут быть графиками функции y=logax, если 0<a<1?
Какие из следующих графиков и по какой причине немогут быть графиками функции y=logax, если 0<a<1?
y
y
x
0 1
a)
y
x
0 1
b)
+
0
+
1
c)
y
y
1
0
d)
+
1
x
0
e)
+
1
x
x
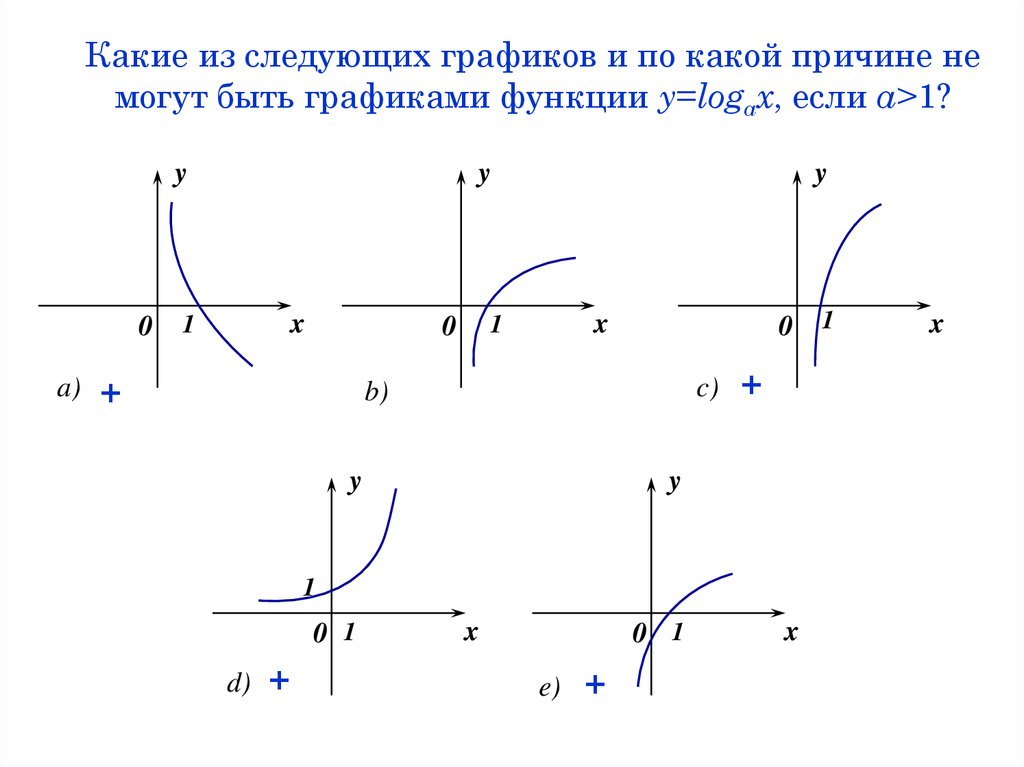
42. Какие из следующих графиков и по какой причине не могут быть графиками функции y=logax, если a>1?
Какие из следующих графиков и по какой причине немогут быть графиками функции y=logax, если a>1?
y
0
a)
y
x
1
x
1
0
+
y
0
c)
b)
y
+
y
1
0 1
d)
+
x
0 1
e)
+
x
1
x
43.
9y
7
5
3
1
-5
-3
-1-1
-3
-5
x
1
3
5
7
44. 4). Тригонометрические функции
y = sin xy = cos x
y = tan x
y = cot x
45. y = sin x
• График функции – синусоида• sin (-x) = - sin (x)
• sin (x+2πk) = sin x
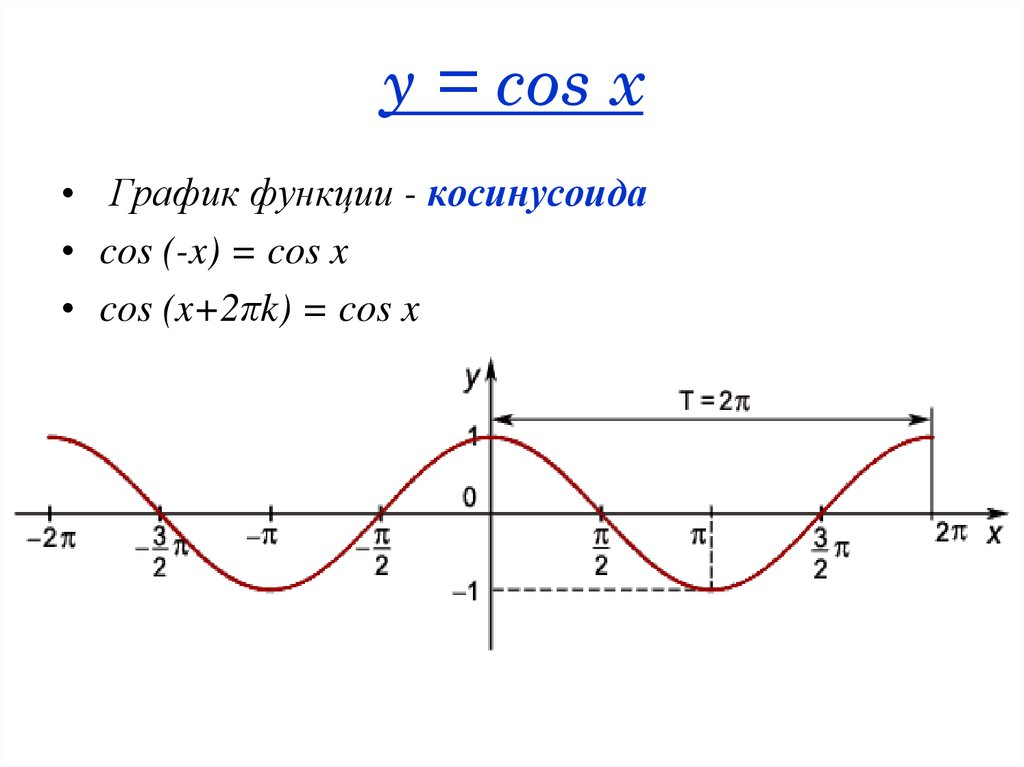
46. y = cos x
• График функции - косинусоида• cos (-x) = cos x
• cos (x+2πk) = cos x
47. y = tan x
• График функции – тангенсоида• tan (-x) = - tan x
• tan (x+πk) = tan x
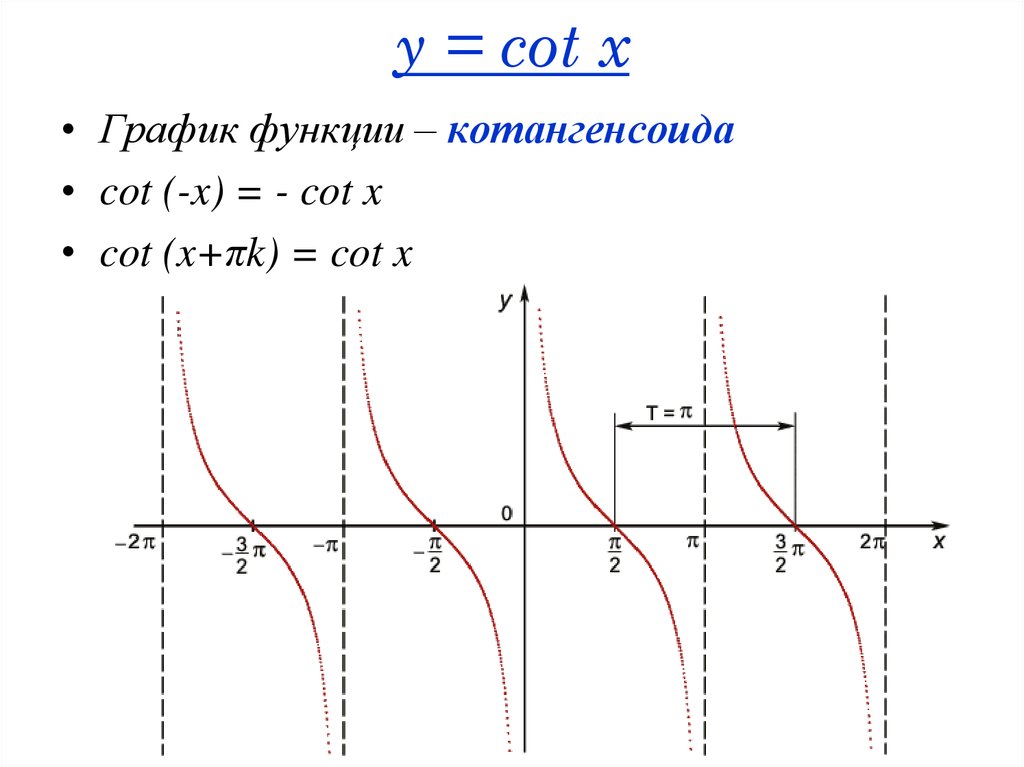
48. y = cot x
• График функции – котангенсоида• cot (-x) = - cot x
• cot (x+πk) = cot x
49. 5). Обратные тригонометрические функции
y = arcsin xy = arccos x
y = arctan x
y = arccot x
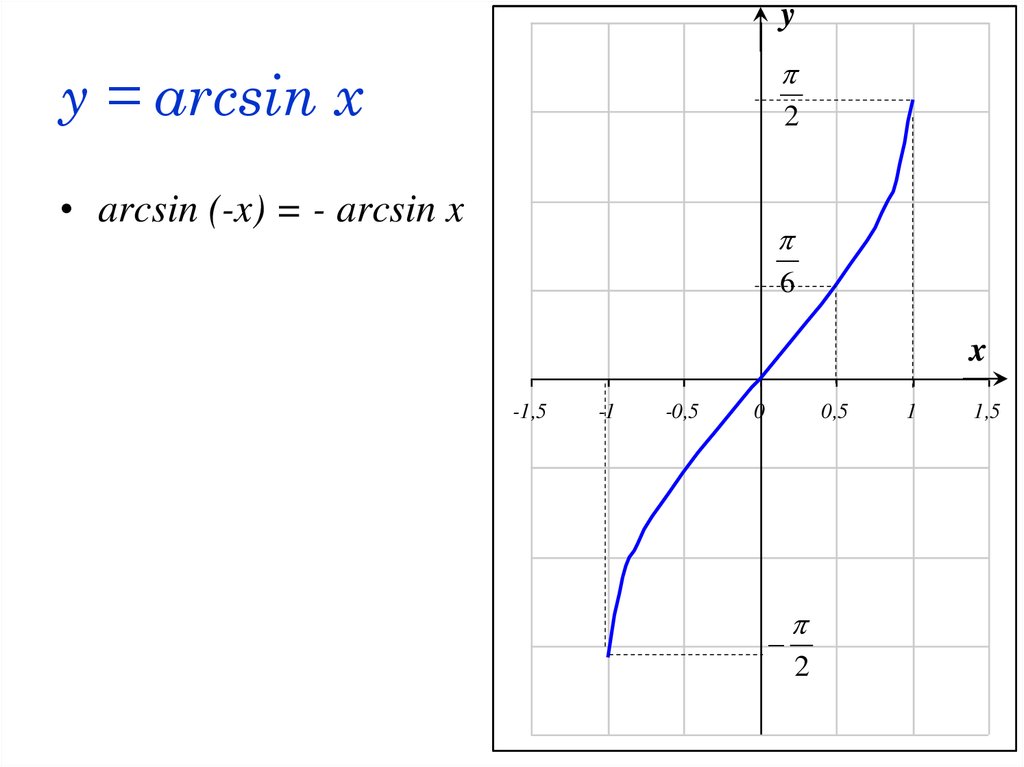
50. y = arcsin x
yy = arcsin x
2
• arcsin (-x) = - arcsin x
6
x
-1,5
-1
-0,5
0
0,5
2
1
1,5
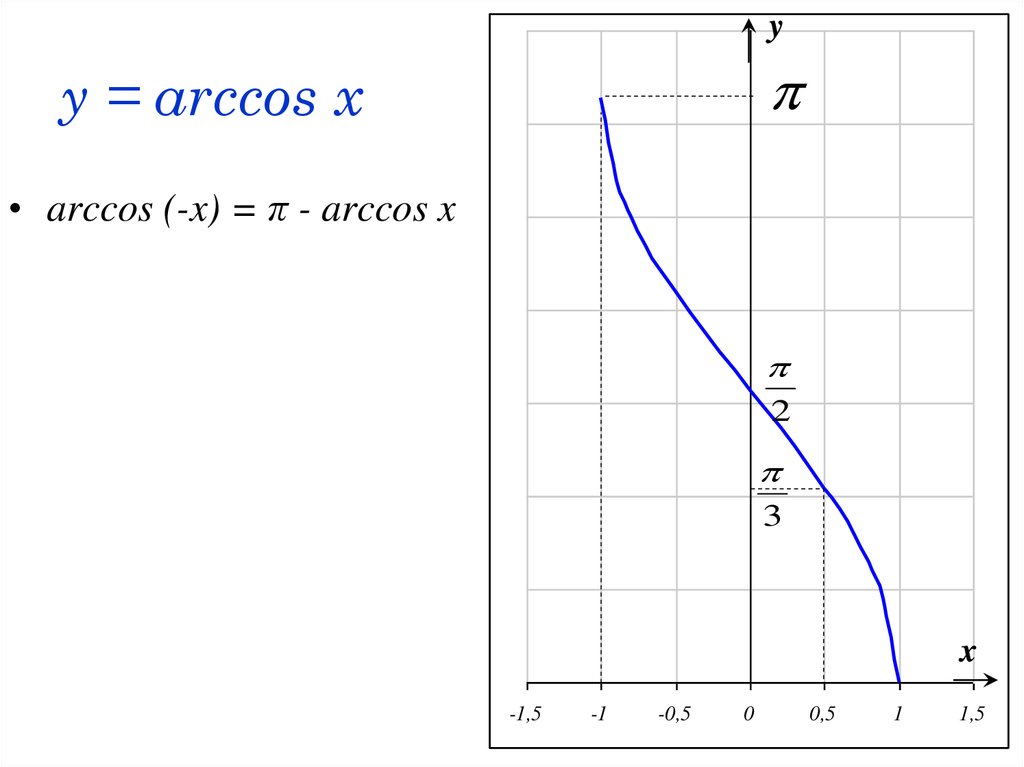
51. y = arccos x
yy = arccos x
• arccos (-x) = π - arccos x
2
3
x
-1,5
-1
-0,5
0
0,5
1
1,5
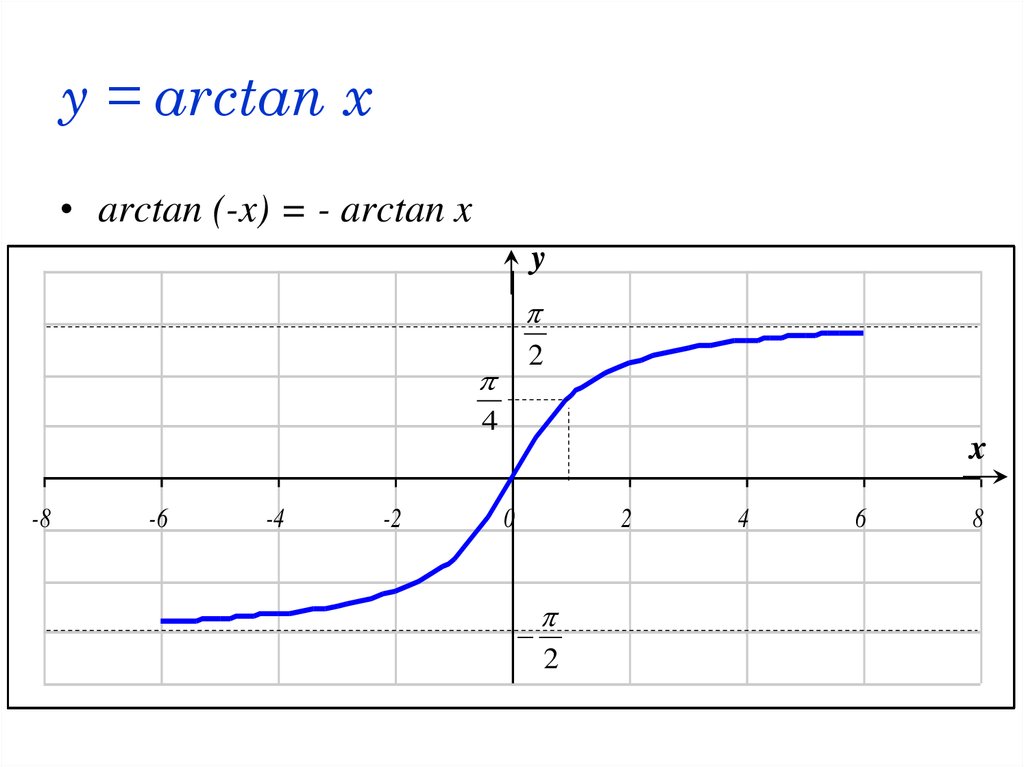
52. y = arctan x
• arctan (-x) = - arctan xy
2
4
-8
-6
-4
-2
x
0
2
2
4
6
8
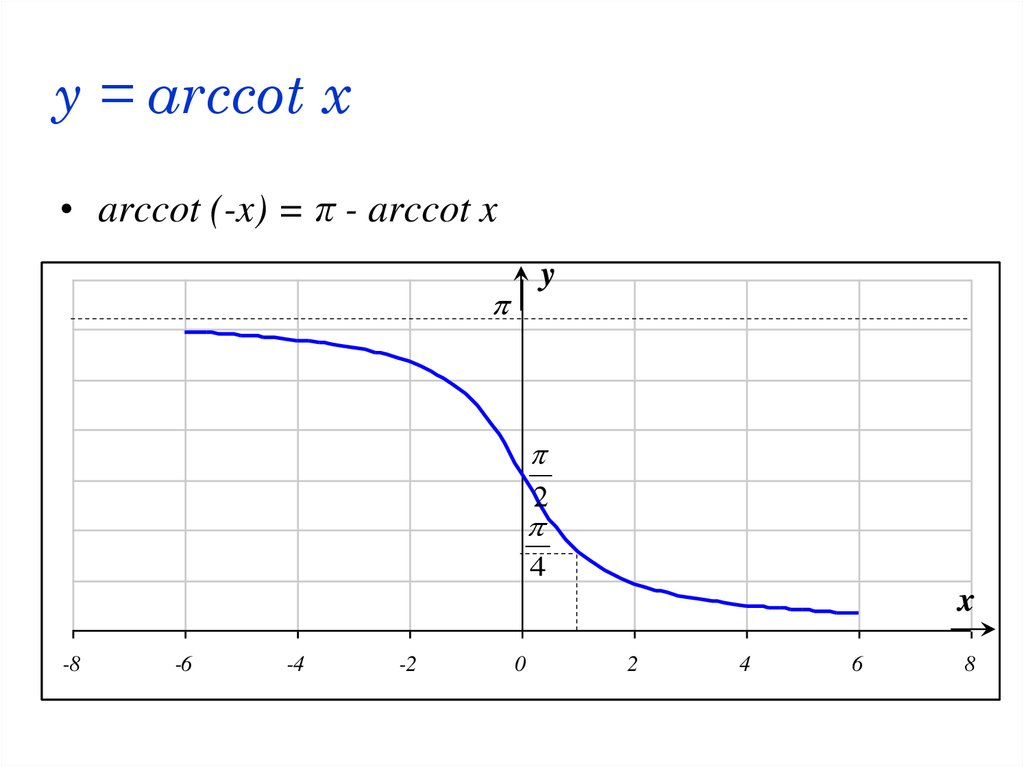
53. y = arccot x
• arccot (-x) = π - arccot xy
2
4
x
-8
-6
-4
-2
0
2
4
6
8
54.
• Функция,задаваемая
одной
формулой,
составленной
из
основных
элементарных
функций и постоянных с помощью конечного
числа арифметических операций (+, -, ·, ) и
операций взятия функции от функции, называется
элементарной функцией.
1
tan x
y arcsin 2
x 8x 3
y x x2
примеры элементарных функций
y log 2 x 3
55.
Примеры неэлементарных функций:1, x 0
y signx 0, x 0
1, x 0
3
5
7
2 n 1
x
x
x
x
n
y 1
... 1
...
2n 1 ! 2n 1
3! 3 5! 5 7! 7
(Количество операций, которое нужно произвести для получения у, не
является ограниченным)
56. 5. Сложение графиков функций
• Чтобы сложить графики функций нужносложить их ординаты.
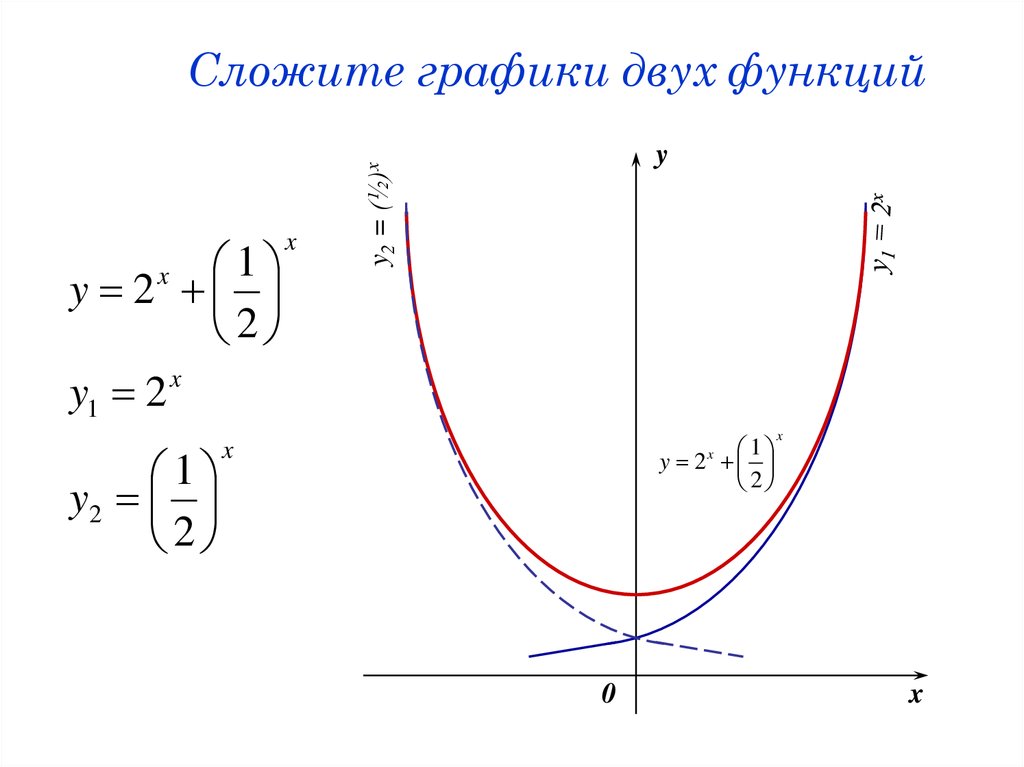
• y = y1+y2
57. Сложите графики двух функций
1y2
2
y2 = (½)x
1
y 2
2
y1 2 x
x
x
y
1
y 2
2
x
x
x
0
x
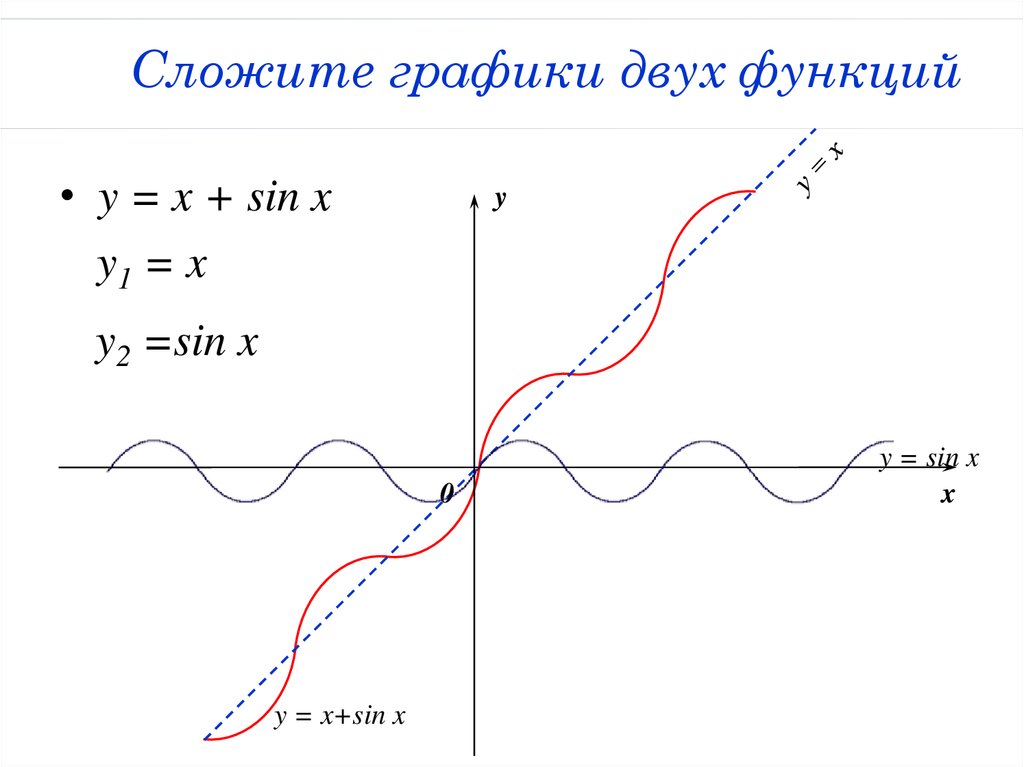
58. Сложите графики двух функций
• y = x + sin xy1 = x
y
y2 =sin x
0
y = x+sin x
y = sin x
x
59. Повторение: ещё некоторые функции Постоянная функция
yc
0
y c, c R
x
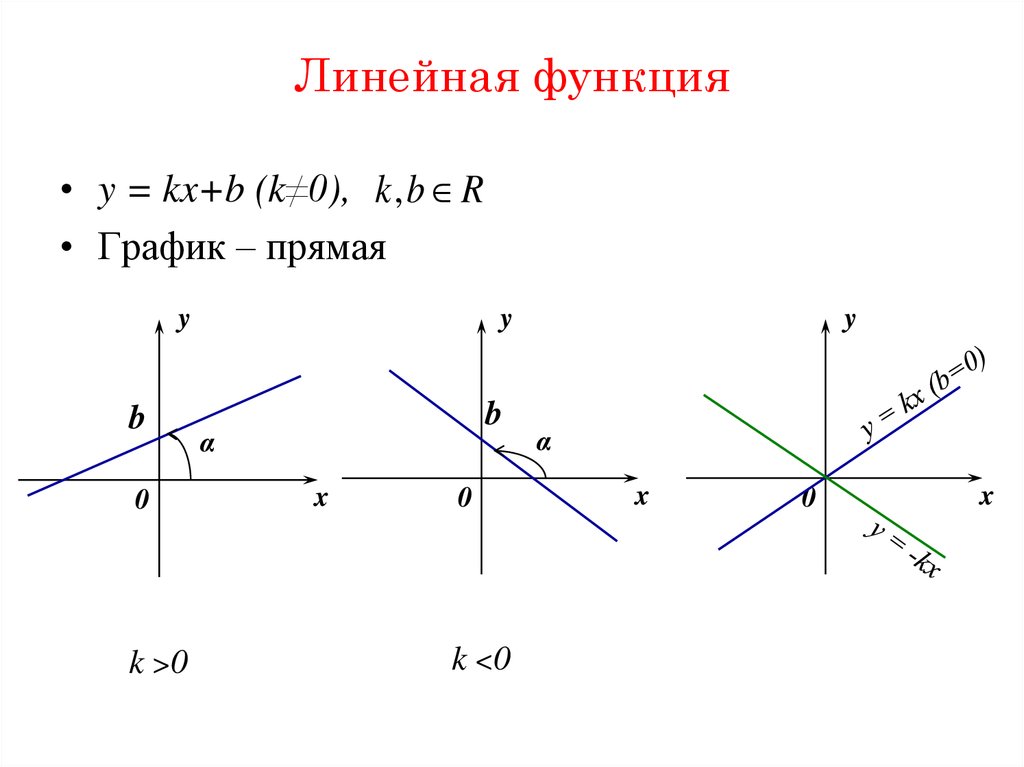
60. Линейная функция
• y = kx+b (k≠0), k , b R• График – прямая
y
b
0
k >0
y
b
α
x
0
k <0
y
α
x
0
x
61.
y8
6
4
2
x
0
-6
-4
-2
0
-2
2
4
6
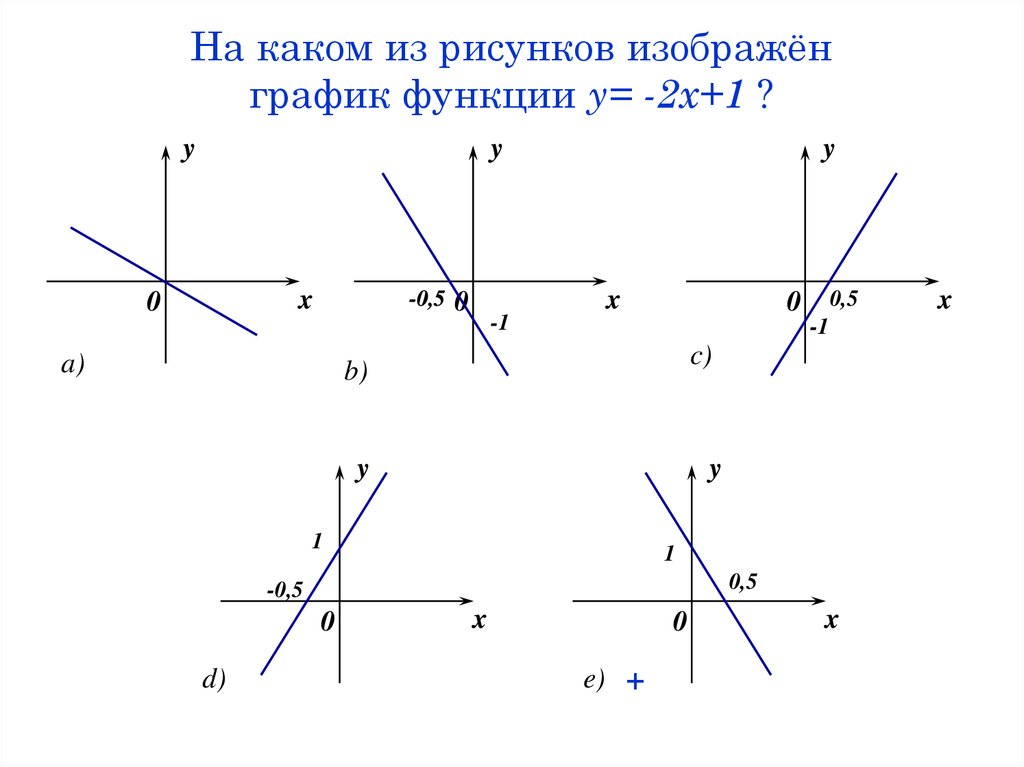
62. На каком из рисунков изображён график функции y= -2x+1 ?
yy
x
0
-0,5
a)
0
-1
y
x
-1
c)
b)
y
y
1
1
0,5
-0,5
0
d)
0,5
0
x
0
e) +
x
x
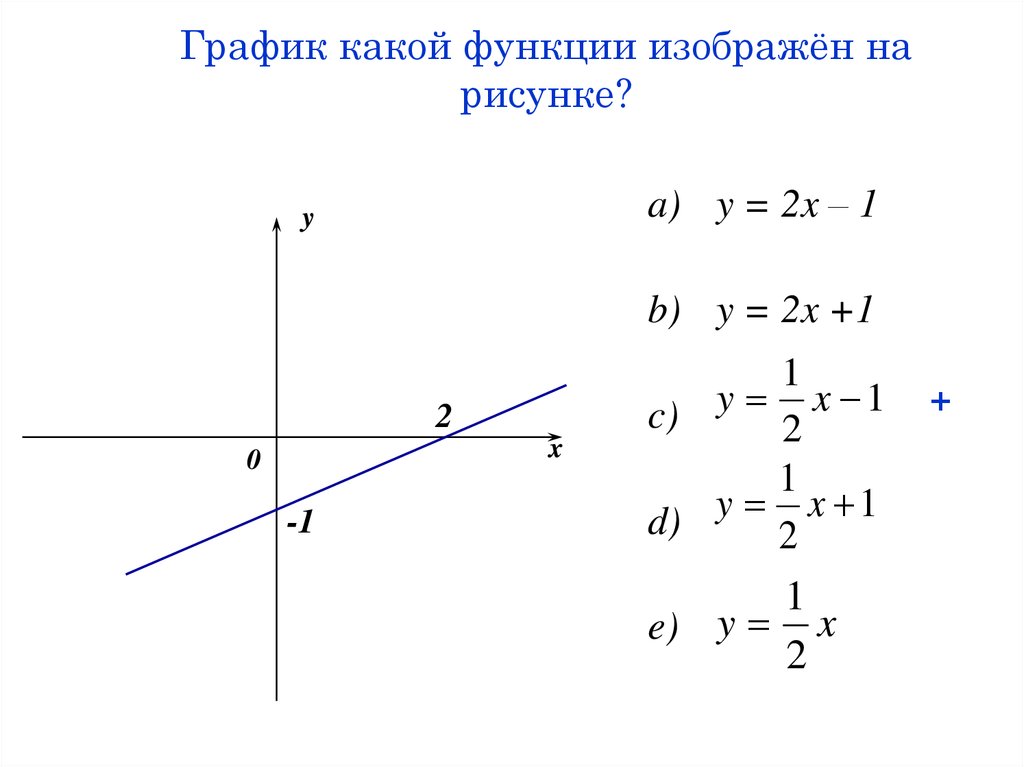
63. График какой функции изображён на рисунке?
a) y = 2x – 1y
b) y = 2x +1
2
x
0
-1
1
c) y 2 x 1
1
d) y 2 x 1
1
e) y x
2
+
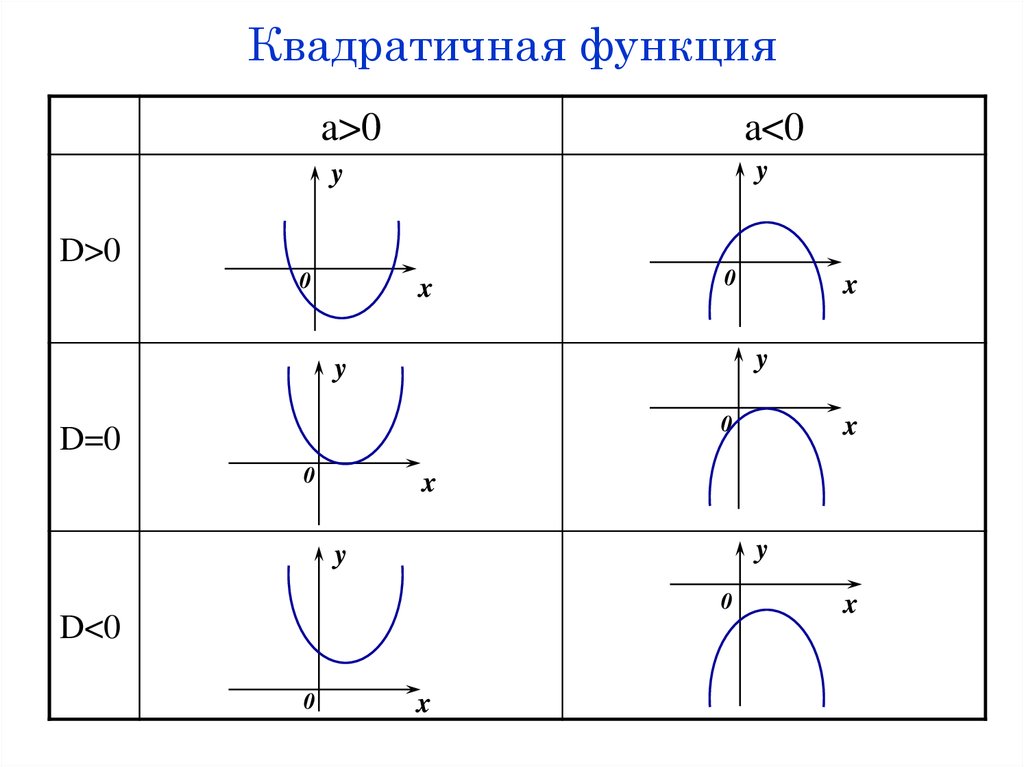
64. Квадратичная функция
• y = ax2+bx+c, a, b, c R , a ≠ 0• График – парабола
D b 4ac
2
b D
x1, 2
2a
b
xв
2a
65. Квадратичная функция
a>0a<0
y
y
D>0
0
x
0
x
y
y
x
0
D=0
0
x
y
y
0
D<0
0
x
x
66. y = |x|
x, x 0y | x |
x, x 0
y
0
x

















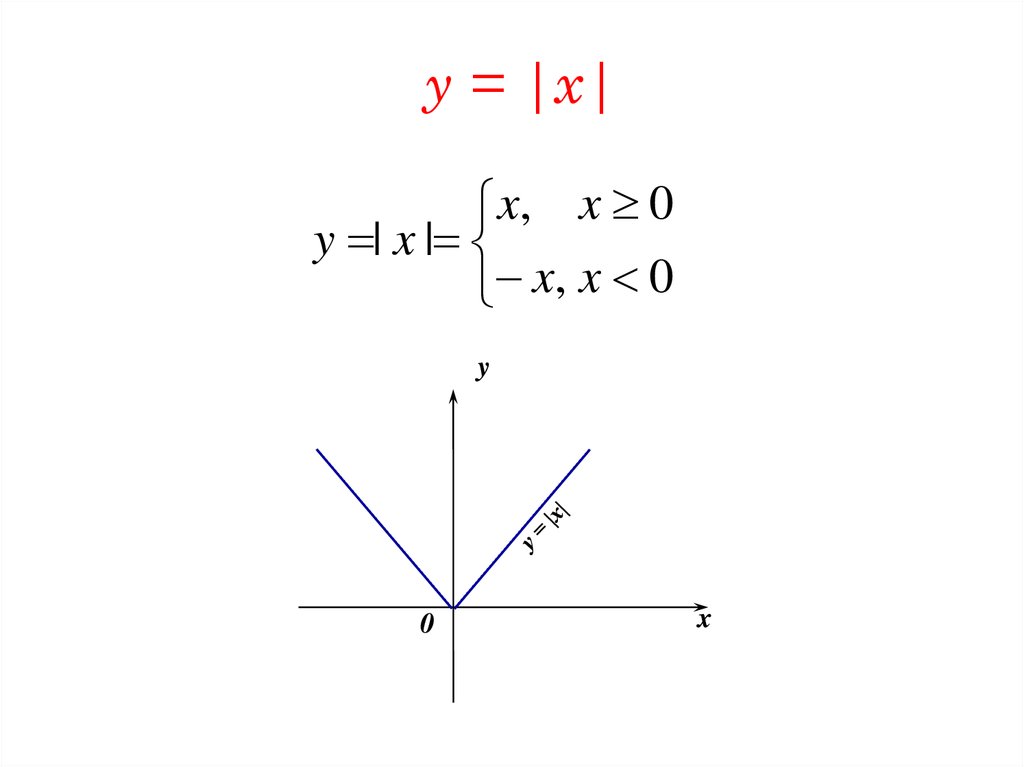
 Математика
Математика








