Решение полного квадратного уравнения

2.

Решение полного квадратного
уравнения.
ax bx c 0
2
2
D 0
b
- дискриминант
x
0
4ac квадратного
2a
уравнения
b
x
0
2a
- корней нет
b
x
- один корень
2a
D 0
- два корня
D b
2
D 0
x1,2
b D
2a

3.

Проверка домашней работы
1) 5 х 18 х 16 0
2
2) 8 х х 75 0
2
3) 4 х 7 х 3 0
2
4) х х 56 0
2
5) х х 1 0
2
4
х1 1 ; х2 2
5
1
х1 3 ; х2 3
8
3
х1 ; х2 1
4
х1 7; х2 8
1 5
1 5
х1
; х2
2
2

4
х1 1 ; х2 2
5
1
х1 3 ; х2 3
8
3
х1 ; х2 1
4
В
и н в е т
Замените целые корни
уравнений на
соответствующие буквы и
отгадайте фамилию
ученого, французского
математика.
И
Е
Т
х1 7; х2 8
1 5
1 5
х1
; х2
2
2
3 1 2 -1 8

5.

Франсуа́ Вие́т
(1540 — 13 февраля 1603)
французский математик,
основоположник
символической алгебры.
По образованию и
основной профессии —
юрист.

6.

Тема урока:
«ТЕОРЕМА
ВИЕТА»

7.

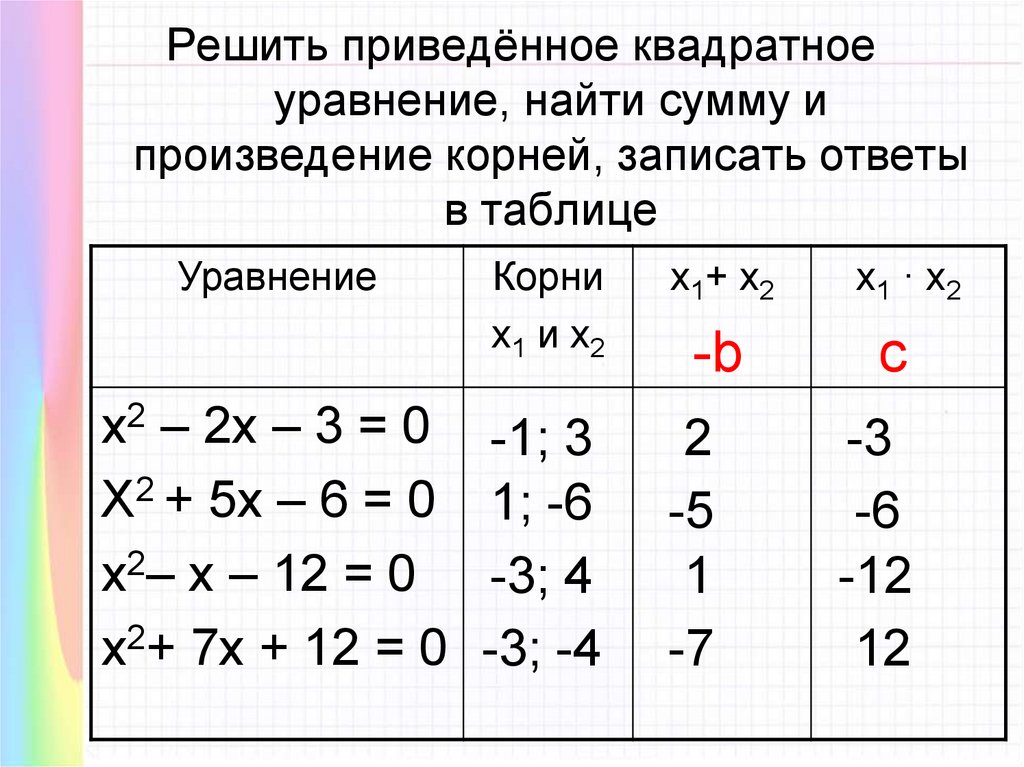
Решить приведённое квадратное
уравнение, найти сумму и
произведение корней, записать ответы
в таблице
Уравнение
х2 – 2х – 3 = 0
Х2 + 5х – 6 = 0
х2– х – 12 = 0
х2+ 7х + 12 = 0
Корни
х1 и х2
х 1+ х 2
-1; 3
1; -6
-3; 4
-3; -4
2
-5
1
-7
-b
х1 · х2
c
-3
-6
-12
12

8.

Теорема Виета.
Если числа х1 и х2
являются корнями уравнения
х2+рх+q=0
то справедливы формулы
x1 x2 q
x1 x2 p
т.е.сумма корней приведённого квадратного
уравнения равна второму коэффициенту,
взятому с противоположным знаком, а
произведение корней равно свободному
члену.

9.

D>0
Найти D
D
Найти корни х1
и х2;
Найти сумму
х1 и х2;
Найти
произведение
х1и х2.
D=0
p 4q
2
p p 2 4q
x1,2
2
р D p D
2
p
( р
D )( p D )
4
р2 D
p 2 p 2 4q
4
4
q
p 2 4q
0
х1, 2
р
2
р р
2
2
р
2
p
q
4

10.

Таблица знаков корней
c
Знаки корней
+
+
+
-
-
+
-
-
Оба корня
положительны
Большее по модулю
число положительно
Оба корня
отрицательны
Большее по модулю
число отрицательно
-b

11.

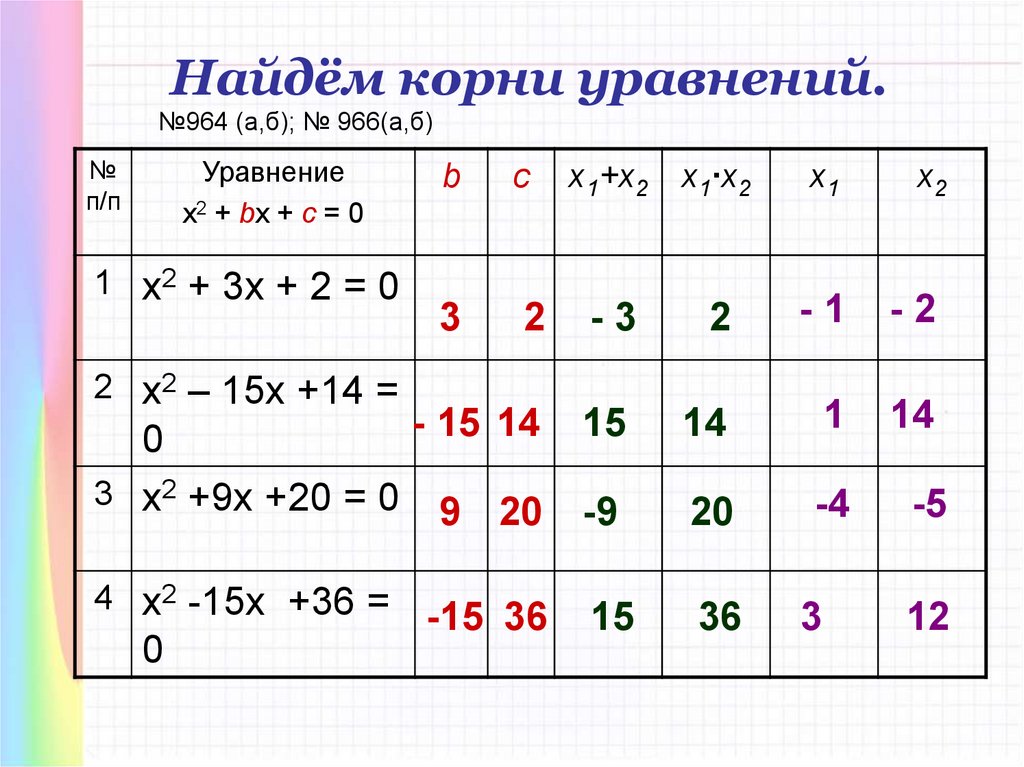
Найдём корни уравнений.
№964 (а,б); № 966(а,б)
№
п/п
Уравнение
х2 + bx + c = 0
1 х2 + 3x + 2 = 0
2 х2 – 15x +14 =
b
c
x1+x2 x1∙x2
0
x2
2
-3
2
-1
-2
- 15 14
15
14
1
14
20
-4
3
0
3 х2 +9x +20 = 0
9 20 -9
4 х2 -15x +36 =
x1
-15 36
15
36
3
-5
12

12.

Теорема, обратная
теореме Виета.
p, q, x1 , x2
Если числа
таковы, что
x1 x2 p, x1 x2 q
то x1 и x2 - корни уравнения
x px q 0
2

13.

1. Пусть х1 и х2 - корни квадратного уравнения (х1 < х2). Решите
уравнение (1-10), запишите корни уравнения в указанном порядке (при
решении там, где это удобно, пользуйтесь теоремой, обратной теореме
Виета).
1) х2-25=0,
(х1,х2)
1) х2-4х-21=0,
(х1,х2)
2) х2-3х=0,
(х1,х2)
2) х2-10х+21=0, (х1,х2)
3) х2-5х+6=0,
(х2,х1)
3) х2-7х+12=0,
(х1,х2)
4) х2-12х+35=0, (х2,х1)
4) х2-6х=0,
(х2,х1)
5) х2-6х=0,
(х2,х1)
5) х2+4х-32=0,
(х2,х1)
6) х2-2х-35=0,
(х2,х1)
6) х2+6х-55=0,
(х2,х1)
7) х2-х-6=0,
(х2,х1)
7) х2+16х+55=0, (х2,х1)
8) х2+3х=0,
(х2,х1)
8) х2+12х+32=0, (х2,х1)
9) х2+10х+25=0, (х1,х2)
9) х2+6х=0,
(х1,х2)
10) х2+10х=0.
10) х2-х-12=0.
(х1,х2)
(х1,х2)
После решения уравнений, полученные точки нанесите на координатную
плоскость, и последовательно соедините все точки.

14.

15.

Задание исследовательского характера
1-я группа.
В уравнении х2+pх-35=0 один из
корней равен 7. Найдите другой корень
и коэффициент p.
2-я группа.
Один из корней уравнения х2-13х+q=0
равен 12,5. Найдите другой корень
уравнения и коэффициент q.
3-я группа (группа сильных учащихся).
Не решая уравнение х2-2х-8=0,
применяя теорему Виета, вычислите
сумму квадратов его корней.

16.

I группа
II группа
х рх 35 0
х 13 х q 0
х1 7
х1 12,5
х1 х2 р
х1 х2 13
х1 х2 35
х1 х2 q
7 х2 35
12,5 x2 13
х2 5
х2 0,5
р 7 ( 5) 2
q 12,5 0,5 6,25
р 2
q 6,25
Ответ : 5; 2
Ответ : 0,5;6,25
2
2

17.

III группа
х1 х2 х1 2 х1 х2 х 2 х1 х2
2
2
2
( х1 х2 ) 2 2 х1 х2
х2 2х 8 0
х1 х2 2
х1 х2 8
2 2 ( 8) 20
2
Ответ : 20
2
2

18.

Подведение итогов
Ответьте на вопросы:
• Какие уравнения мы сегодня
рассматривали?
• Чему равна сумма корней квадратного
уравнения?
• Чему равно произведение корней
квадратного уравнения?
Продолжите фразы:
• Сегодня на уроке я узнал...
• Сегодня на уроке я научился...
• Сегодня на уроке я познакомился...

19. Домашнее задание

1, 2 уровень: №№965-967 (в,г) о каком
событии говорят коэффициенты
уравнения
12х2 + 4х + 1961 = 0. Найти корни уравнения.
3 уровень: №997,

English Русский Правила