Преобразование тригонометрических выражений

1. Преобразование тригонометрических выражений

«Три пути ведут к знанию:
путь размышления – это путь самый
благородный,
путь подражания – это путь самый лёгкий,
и путь опыта – это путь самый горький»
Конфуций

2. Верно ли, что

… существует такое число t,что sin t =- 0,8, cos t= 0,6;
… косинус положительного аргумента может
принимать отрицательные значения;
… уравнение cos x = π имеет множество корней;
… значение выражения (cos x – sin x)² + 2sin x cos x
не зависит от значения х;
… tg 3 > 0;
… корни уравнения sin x = a имеют вид:
x = ± arcsin x + 2πk, k є Z;
… cos (- x) = - cos x;
3
… sin 150⁰ = 0,5, а cos 150⁰ = 2 ;
1
… arccos (- ) = - 3 ;
2
… уравнение sin x = 1 – особенное?

3. Преобразование тригонометрических выражений

4. Проверочный тест В – 1

А1. Найдите cos2α, если sin α = 1)
3
2
2)
3
2
3
2
3) - 0,5
, π < α < 3π/2.
4) 0,5
А2. Найдите значение выражения
если α = 46⁰, β = 74⁰.
cos 2 sin sin
3)1
2)0,5
1) 0,5
4) 1
1,5 sin 2 х 3,5
А3. Укажите наименьшее значение выражения
4
1) 2
2)1
3)2,5
В1. Вычислите
2 sin 310 cos 310
sin 380 sin 660 cos 380 sin 240
Ответ: 1.
4) 1

5. Проверочный тест В - 2

А1. Найдите cos α, если sin α = 12 и α - угол II четверти.
13
5
1)
13
5
2)
13
1
3)
13
4)
5
12
А2. Найдите значение выражения 2sin 15⁰(cos 10⁰ cos 5⁰ - sin 10⁰ sin 5⁰)
1)1
2) 2
3)0,25
4)0,5
А3. Найдите наибольшее значениевыражения 3 cos(2 x - 4 ) – 2,5
1)3
2)0,5
3)5,5
4) 0,5
3
В1. Найдите значение выражения 6 2 tg α cos²(π – α), если sin 2α = 2
Ответ: 2.

6.

В1. Решение:
2 sin 310 cos 310
0
0
0
0
sin 38 sin 66 cos 38 sin 24
sin 620
0
0
0
0
0
sin 38 sin( 90 24 ) cos 38 sin 24
sin 620
0
0
0
0
sin 38 cos 24 cos 38 sin 24
sin 620
sin 620
1
0
0
0
sin( 38 24 ) sin 62

7.

В1. Решение:
sin
2
6 2 tg cos ( ) 6 2
cos
cos
2
3 2 2 sin cos 3 2 sin 2 3 2
2
3
2

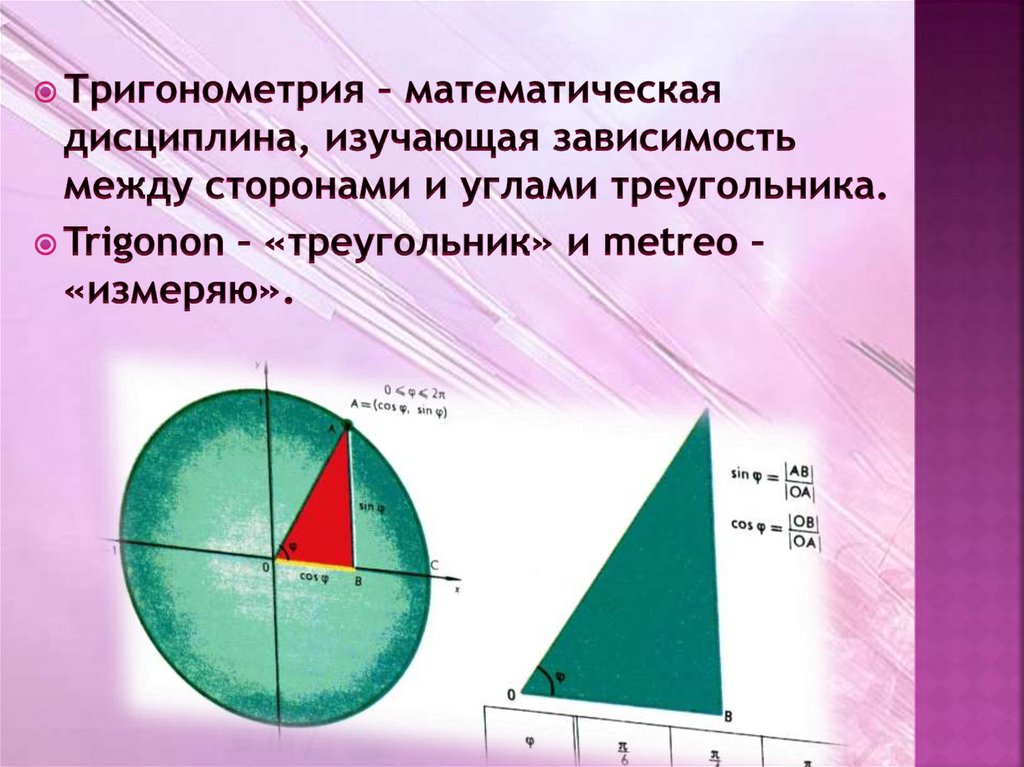
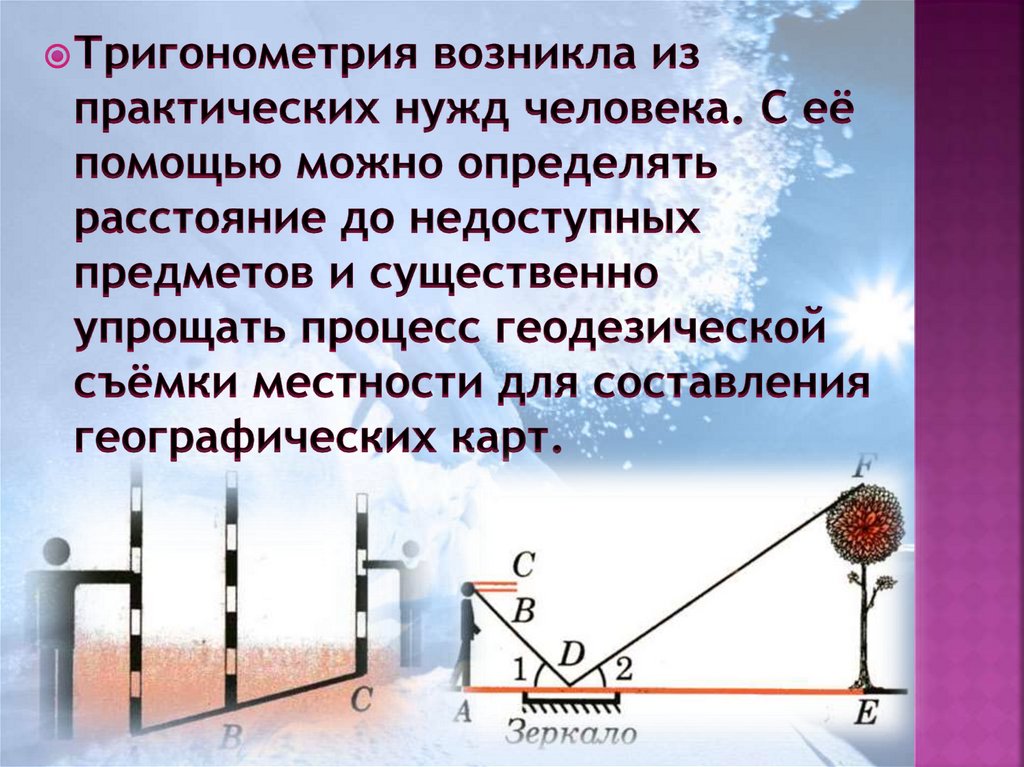
8. История возникновения тригонометрии

Презентацию подготовил ученик 10Б класса
Царегородский Александр

9.

10.

11. Возникновение

12.

13.

14.

15.

16.

17. Использованная литература

Энциклопедический
словарь юного
математика/Сост. А.П.Савин.-М.:
Педагогика, 1989.
Интернет-ресурсы.

18. Преобразование тригонометрических выражений

19.

Задание
Найдите
наибольший
отрицательный
корень
уравнения
sin 3x cos 5x –
- cos 3x sin 5x =
= 0,5
Алгоритм
решения
Базовые знания
Применим
формулу
синуса
разности.
sin(x-y) =
=sinx cosy –
-cosx siny
Воспользуемся
формулой
корней
уравнения
sinx = a.
x =(-1)ⁿarcsina+
+ πn,
nЄZ
Найдём
наибольший
отрицательный
корень
уравнения.
Конкретные шаги
решения
sin 3x cos 5x –
-cos 3x sin 5x = 0,5
sin(3x – 5x) = 0,5
sin 2x = - 0,5
2x = (-1)ⁿ(-π/6) + πn
n
x ( 1) n 1
12 2
nЄZ
При n = 0 x = - 12
Ответ: -
12

20.

Задание
Алгоритм
решения
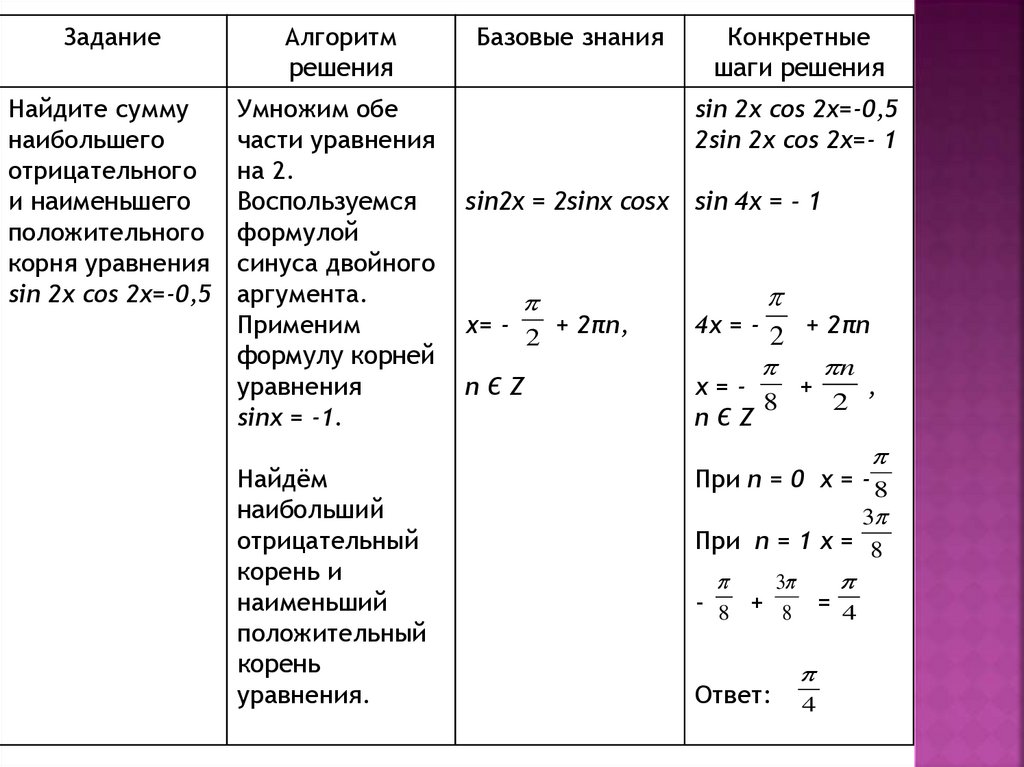
Найдите сумму
наибольшего
отрицательного
и наименьшего
положительного
корня уравнения
sin 2x cos 2x=-0,5
Умножим обе
части уравнения
на 2.
Воспользуемся
формулой
синуса двойного
аргумента.
Применим
формулу корней
уравнения
sinx = -1.
Найдём
наибольший
отрицательный
корень и
наименьший
положительный
корень
уравнения.
Базовые знания
Конкретные
шаги решения
sin 2x cos 2x=-0,5
2sin 2x cos 2x=- 1
sin2x = 2sinx cosx
х= - 2 + 2πn,
nЄZ
sin 4x = - 1
4x = - 2 + 2πn
n
x=+
,
2
8
nЄZ
При n = 0 x = - 8
3
При n = 1 x = 8
3
- 8 + 8
Ответ:
= 4
4

21.

Задание
Алгоритм
решения
Сколько корней
уравнения
sin2x+ sin6x = 0
принадлежат
промежутку
[-180⁰; 180⁰] ?
Применим
формулу
суммы синусов
Базовые знания
sinx + siny =
=2sin x y cos x y
2
2
Конкретные шаги
решения
sin 2x sin 6x = 0
2sin 4x cos 2x = 0
sin4x = 0 cos2x = 0
4x = πn
2x = + πk
Воспользуемся
условием
2
равенства
n
произведения 0
x
=
4
и формулами
x = πn, x = +πk
k
2
корней
x= 4 2
уравнений
n Є Z, k Є Z
sinx = 0; cosx =0
n Є Z, k Є Z
Оценим корни
уравнения
- π ≤ n≤ π
4
-4≤n≤4
Ответ: 9 корней.

22. Домашнее задание

Пособие
«Математика ЕГЭ – 2009, часть I»
стр. 204, В - №3, задания 1,2,3,6 – уровень А,
задания 1 – 8 – уровень В,
задачник - № 27.56 а), 28.33 а) – уровень С.

23.

«Три пути ведут к знанию:
путь размышления – это путь самый
благородный,
путь подражания – это путь самый лёгкий,
и путь опыта – это путь самый горький»
Конфуций