Похожие презентации:
Свойства функции. Исследование свойств функции по графику
1. Свойства функции
Исследование свойств функциипо графику
2.
Слово «функция» в математике появилосьсравнительно недавно.
Впервые о функциях стал говорить
великий немецкий математик и философ
Г.
В.Лейбниц
Лейбниц
Г. В.
в конце XVII века,
а первое определение
функции дал его ученик
И. Бернулли
Бернулли
в 1718 году.
Впрочем, это было не то определение,
которым
мы
пользуемся
сегодня.
Определение функций было дано позднее –
в конце XIX века.
3.
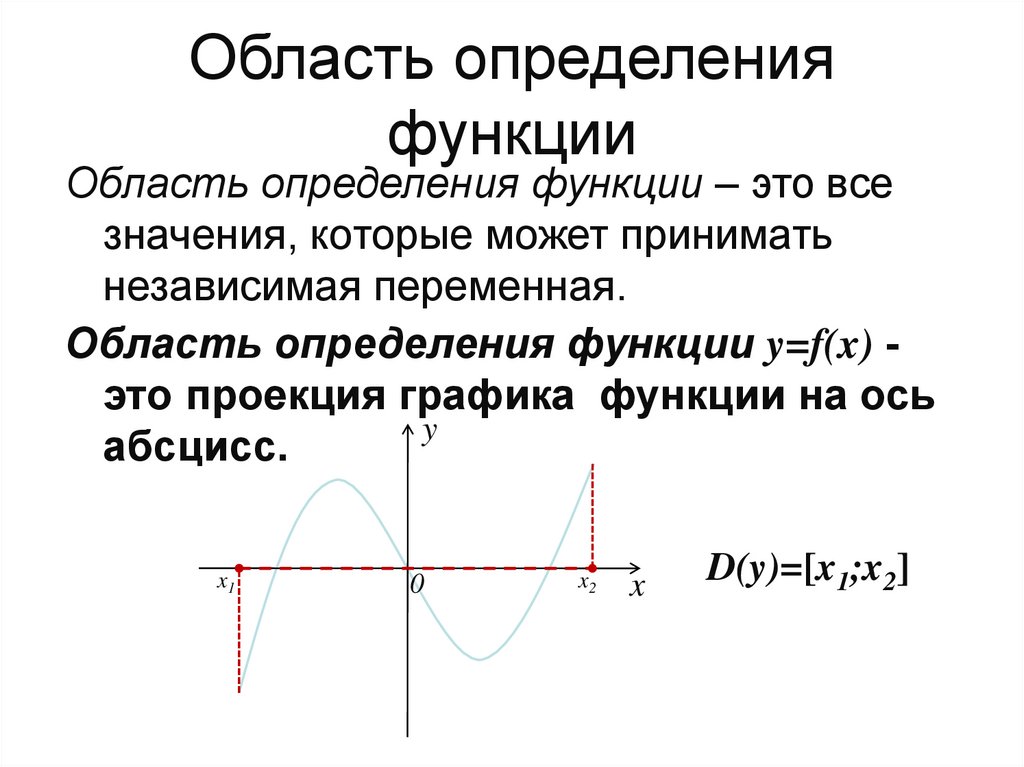
4. Область определения функции
Область определения функции – это всезначения, которые может принимать
независимая переменная.
Область определения функции y=f(x) это проекция графика функции на ось
y
абсцисс.
x1
0
x2
x
D(y)=[x1;x2]
5.
Область определения функцииD( y) 8; 9
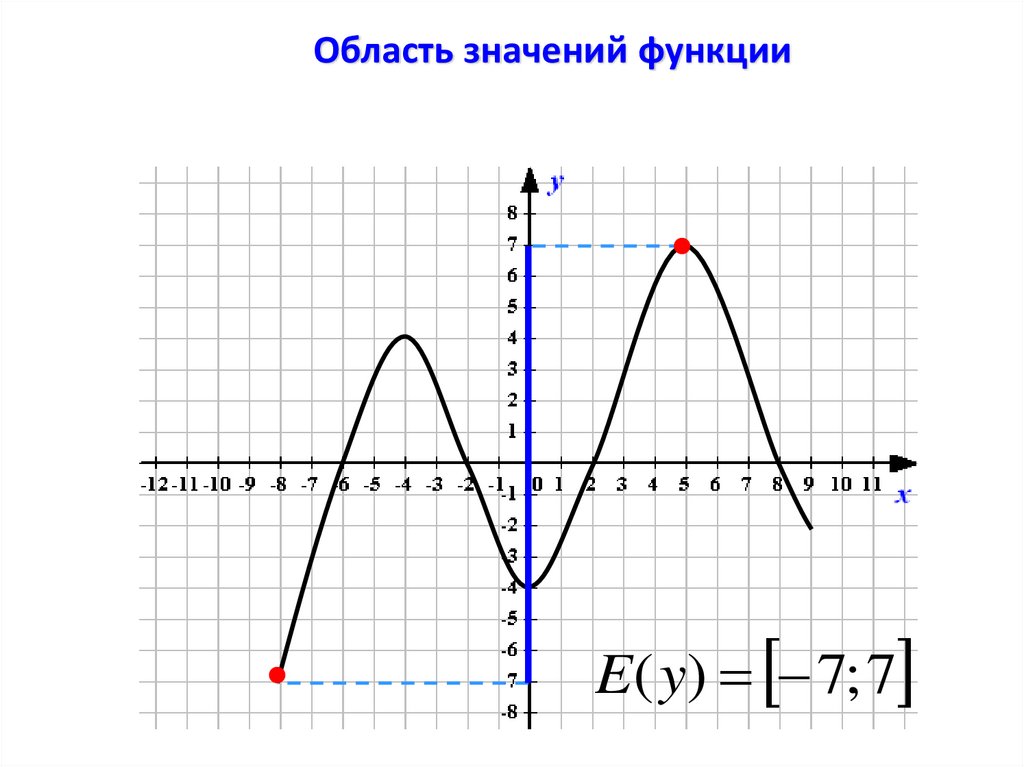
6. Область значений функции
Область значений функции – это всезначения, которые принимает зависимая
переменная.
Область значений функции y=f(x) - это
проекция графика на ось ординат.
y
y2
0
y1
x
E(y)=[y1;y2]
7.
Область значений функцииE( y) 7; 7
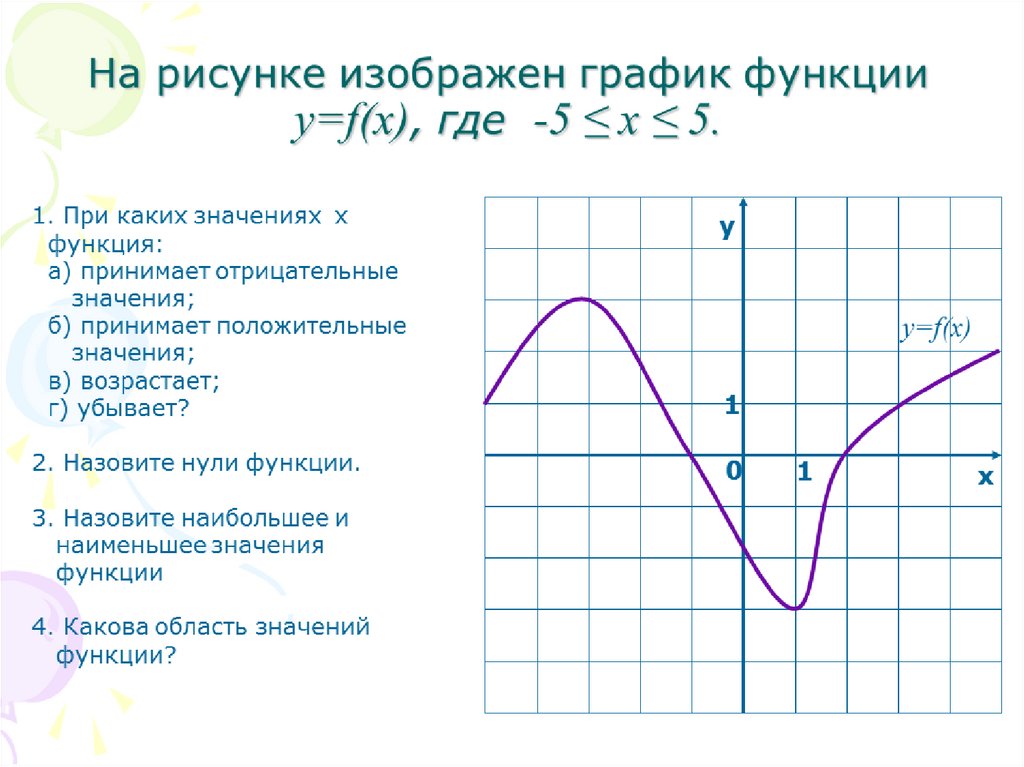
8. Нули функции
Нули функции – это значения аргумента, прикоторых функция обращается в нуль.
Нули функции на плоскости – абсциссы
точек пересечения графика с осью х.
Чтобы найти нули функции y=f(x), нужно
найти корни уравнения f(x)=0. y
x1
x1, x2, x3 – нули функции.
0
x2
x3
x
9.
Нули функцииx 6; x 2;
x 2; x 8
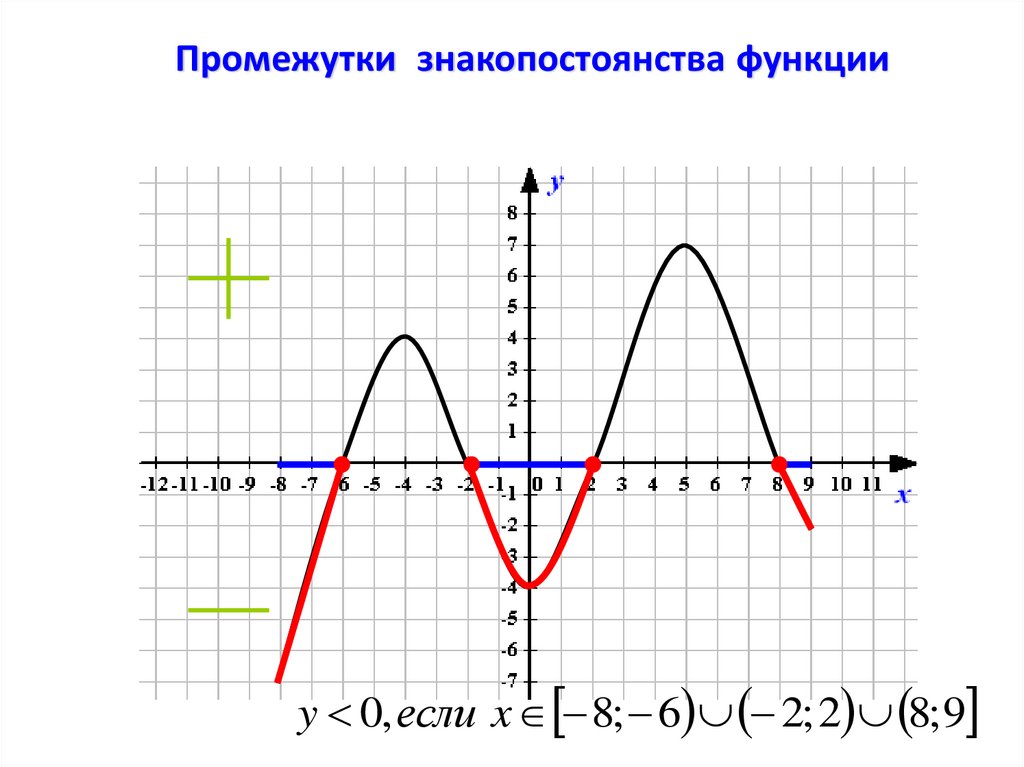
10. Промежутки знакопостоянства
Промежутки знакопостоянства – этопромежутки, в которых функция сохраняет
знак (принимает либо положительные
значения, либо отрицательные).
y
f(x)>0 при x (x1;x2)
f(x)<0 при x (x2;x3)
x1
0
x2
x3
x
11.
Промежутки знакопостоянства функцииy 0, если x ( 6; 2) (2;8)
12.
Промежутки знакопостоянства функцииy 0, если x 8; 6 2; 2 8; 9
13. Промежутки монотонности
yЕсли x2>x1 и y2>y1 => функция возрастающая
y2
x1
0
y1
x2
x
y
y1
x1
0
y2
Если x2>x1 и y2<y1 => функция убывающая
x2
x
14.
Монотонность функцииу возрастает на 8; 4 ; 0; 5
15.
Монотонность функцииу убывает на 4; 0 ; 5; 9
16. Схема исследования функции
Найти область определения функцииНайти область значений функции
Найти нули функции
Найти промежутки знакопостоянства
функции
5. Найти промежутки возрастания и
убывания функции
1.
2.
3.
4.
17. Линейная функция у = kx + b
уk<0
k>0
- b/k 0
х
0 - b/k
х
1 . D (f) = (- ;+ ) 4. Если k > 0, то у > 0 на (- b/k;+ )
у < 0 на (- ; - b/k)
2. E (f) = (- ;+ )
Если k < 0, то у > 0 на (- ; - b/k)
3. Нули функции:
у < 0 на (- b/k;+ )
kx + b = 0
5. При k > 0 функция возрастает
kx == - b
При k < 0 функция убывает
x = - b/k













 Математика
Математика








