Похожие презентации:
كتاب رياضيات و كاربرد آن در مديريت
1. كتاب رياضيات و كاربرد آن در مديريت
كتابرياضيات و كاربرد آن در
مديريت
رشته هاي حسابداري و مديريت
2. مؤلف: ليدا فرخي
مؤلف :ليدا فرخيتهيه ي پاور پوينت :اردوان ميرزايي
تعداد واحد 3 :
3. اهداف درس
اهداف درستوانايي حل مسئله
تقويت تفكر رياضي
آشنايي با :بردارها
ماتريس و دترمينان
دستگاه معادالت خطي و توابع خطي
توابع چند متغيره و معادالت ديفرانسيل
انتگرال
4. فهرست مطالب
فهرست مطالب
فصل اول :بردارها
فصل دوم:ماتريس و دترمينان
فصل سوم :دستگاه معادالت خطي و توابع خطي
فصل چهارم :توابع چند متغيره
فصل پنجم:معادالت ديفرانسيل
فصل ششم :انتگرال
5. فصل اول: بردارها
فصل اول :بردارها
بردارها در صفحه
ضرب عددي دو بردار
بردارها در فضاي سه بعدي
ضرب برداري بردارها
بردارها در فضاي nبعد
6. فصل دوم:ماتريس و دترمينان
فصل دوم:ماتريس و دترمينان
ماتريس
دترمينان
وارون ماتريس
7. فصل سوم: دستگاه معادلات خطي و توابع خطي
فصل سوم :دستگاه معادالت خطي و توابع خطي
دستگاه معادالت
استقالل و وابستگي خطي
رتبه ي يك ماتريس
توابع خطي
8. فصل چهارم: توابع چند متغيره
فصل چهارم :توابع چند متغيره
توابع چند متغيره
حد و پيوستگي توابع چند متغيره
مشتق هاي جزيي
ديفرانسيل كل و مشتقگيري ضمني
ماكسيمم و مينيمم توابع دو متغيره
ماكسيمم و مينيمم توابع نسبت به شرايط داده شده
9. فصل پنجم:معادلات ديفرانسيل
فصل پنجم:معادالت ديفرانسيل
آشنايي معادالت ديفرانسيل
معادالت ديفرانسيل جدايي پذير
10. فصل ششم: انتگرال
فصل ششم :انتگرال
انتگرال
11. فصل اول: بردارها
فصل اول :بردارها12.
كميتهايي مانند سرعت يا شتاب يك متحرك و نيروي وارد بريك جسم هنگامي مشخص مي شوند كه عالوه بر اندازه سو
و جهتشان نيز معين باشد.اين نوع كميت ها را برداري مي
ناميم.
13.
برخي از كميت ها هنگامي كه اندازه ي آنها بر حسب واحدمشخصي داده شود كامال معين مي شوند
.
مانند درجه ي حرارت ،جرم ،طول و حجم ،هزينه و درآمد.
اين گونه كميت ها را عددي يا اسكالر مي ناميم
.
14. 1.1بردارها در صفحه
1.1بردارها در صفحه15. 1.1.1تعريف
1.1.1تعريفپاره خط ABكه ابتداي آن Aو انتهاي آن Bاست ،يك پاره خط
جهت دار ناميده مي شود .به شكل زير توجه كنيد:
B
A
پاره خط جهت دار ABرايك بردار مي ناميم و با ABنمايش ميدهيم
نقطه ي Aرا مبدا و نقطه ي Bرا انتهاي برداَرمي ناميم.
16. 1.1.2 تساوي دو بردار
1.1.2تساوي دو برداردو بردار ABو CDرا برابر يا همسنگ مي ناميم و مينويسيم
، AB=CDاگر اندازه و جهت آنها يكي باشد.
B
D
C
A
17. 1.1.3 جمع بردارها
1.1.3جمع بردارهادو بردار ABو CDرا در نظر مي
گيريم.مجموع AB+CDبرداري است مانند Vكه به يكي
از دو روش زير به دست مي آيد.
با توجه به تعريف تساوي دو بردار ،مي توان دو برداررا كه
داراي يك مبدا نباشند نيز با يكديگر جمع كرد.
18.
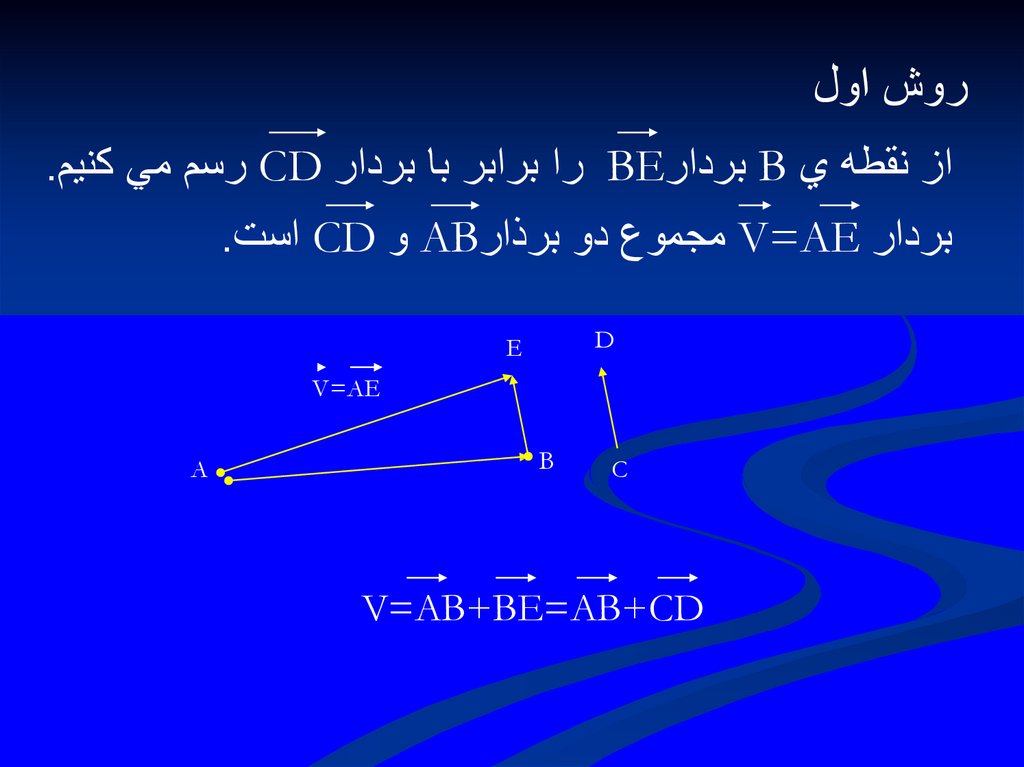
روش اولاز نقطه ي Bبردار BEرا برابر با بردار CDرسم مي كنيم.
بردار V=AEمجموع دو برذار ABو CDاست.
D
E
V=AE
C
B
V=AB+BE=AB+CD
A
19.
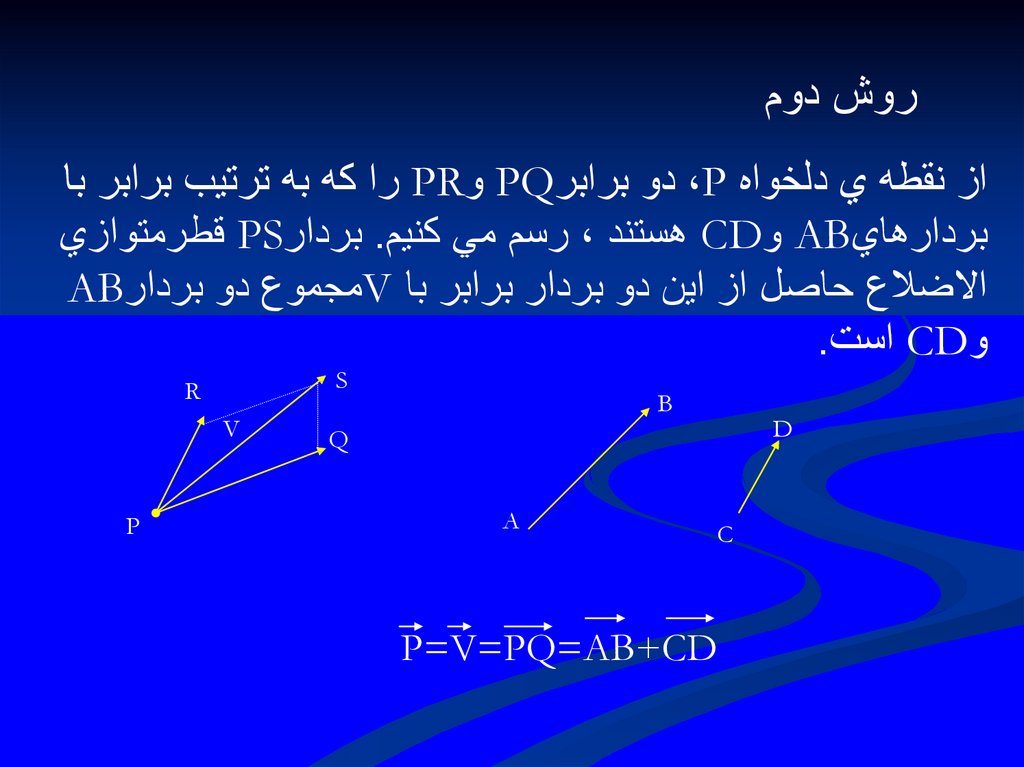
روش دوماز نقطه ي دلخواه ،Pدو برابر PQو PRرا كه به ترتيب برابر با
بردارهاي ABو CDهستند ،رسم مي كنيم .بردار PSقطرمتوازي
االضالع حاصل از اين دو بردار برابر با Vمجموع دو بردارAB
و CDاست.
S
B
D
Q
C
A
P=V=PQ=AB+CD
R
V
P
20. 1.1.4 بردار صفر
1.1.4بردار صفراگر اندازه ي بردار Vبرابر صفر باشد يعني ، V =0
بردار Vرا بردار صفر مي ناميم و 0با نشان مي دهيم .بنا
بر اين اندازه ي 0برابر صفر است ،ولي جهت آن
مشخص نيست.
21. 1.1.5 ضرب عدد در بردا ر(ضرب اسكالر)
1.1.5ضرب عدد در بردار(ضرب اسكالر)
فرض مي كنيم Vبرداري دلخواه و Cعددي حقيقي باشد.منظور
از حاصلضرب عدد Cدر بردار Vبرداري است با اندازه ي
C Vو همجهت با Vاگر C>0و در خالف جهت V
اگر .C<0حاصلضرب عدد Cدر بردار Vرا با CVنشان مي
دهيم.در شكل :اگر C=0آنگاه CVبرابر است با بردار صفر.
CV
V
CV
V
22. 1.1.7 تعريف
1.1.7تعريفبردار Vرا كه ابتداي آن مبدا مختصات و انتهاي آن نقطه ي
)(a1 , a2است در صفحه ي مختصات xoyاست ،بردار
نظير زوج مرتب ) (a1 , a2مي ناميم .اعداد a1و a2را
مؤلفه هاي بردار Vميناميم و مي نويسيم:
)(a1 , a2
a1
)V= (a1 , a2
V
a2
0
23. 1.11 قضيه
1.11قضيهاگر ) V1=(a1,a2و ) V2=(b1,b2دو بردار باشند ،آنگاه
مجموع V1+V2برابر است با:
)V1+V2= (a1+b1 , a2+b2
24. 1.1.13 تعريف قرينه ي يك بردار
1.1.13تعريف قرينه ي يك برداراگر) ،V=(a1,a2آنگاه بردار ) (-a1,-a2را قرينه ي بردارV
مي ناميم و با -Vنشان مي دهيم .پس:
)-V=(-a1, -a2
25. 1.1.14 تعريف تفاضل دو بردار
1.1.14تعريف تفاضل دو برداربردار ) V+(-Uرا كه مساوي با جمع Vبا قرينه ي Uاست
تفاضل Uاز Vمي ناميم و با V-Uنشان مي دهيم .يعني:
)V-U=V+(-U
26. 1.15 تعبير هندسي تفاضل دو بردار
1.15تعبير هندسي تفاضل دو بردارنمايش هاي دو بردار Vو Uرا از يك نقطه رسم مي كنيم.
در اين صورت ،پاره خط جهت داري كه مبدا آن نقطه ي
انتهايي نمايش Uو انتهاي آن ،نقطه ي انتهايي نمايش V
باشد ،يك نمايش بردار V-Uاست .زيرا بنا بر تعريف
جمع بردارها داريم:
U+(V-U)=V
27. 1.1.16 اندازه ي يك بردار
1.1.16اندازه ي يك برداراندازه ي بردار ) V=(a1,a2برابر است با:
2
2
V = a1+a2
28. 1.1.18 قضيه
1.1.18قضيهاگر Vو Uو Wبردارهايي در Vxبوده و cو dاعدادي حقيقي
باشند ،آنگاه جمع برداري و ضرب اسكالر داراي خواص
زيرند:
( U+V=V+Uقانون جا به جايي جمع)
( U+(V+W)=(U+V)+W قانون شركت پذيري جمع)
برداري مانند 0در Vوجود دارد به طوري كهV+0=V
(وجود هماني نسبت به عمل جمع)
برداري مانند -Vو Vدر هست به طوري كه
(V+(-V)=0وجود قرينه ي هندسي نسبت به عمل جمع)
29. ادامه
ادامه
) ( (cd) V=c (dVقانون شركت پذيري)
( C (U+V)=cU+cVقانون بخشپذيري)
( (c+d)U=cU+dUقانون بخشپذيري)
( +- U=Uوجود هماني نسبت به ضرب اسكالر)
30. 1.1.20 تعريف فضاي برداري حقيقي
1.1.20تعريف فضاي برداري حقيقيفضاي برداري حقيقي Vمجموعه اي است از بردارها ،همراه
با مجموعه اعداد حقيقي ( اسكالرها) ،با دو عمل جمع
برداري و ضرب اسكالر ،به طوري كه هر جفت بردارU
و Vدر Vو هر اسكالر ، cبردارهاي U+Vو cUطوري
تعريف شده باشند كه در خواص قضيه ي قبل صدق كنند.
31. بردارهاي يكه
بردارهاي يكهاندازه ي هر دو بردار (0و )1و(1و ، )0برابر با 1است،
آنها را بردارهاي يكه مي ناميم و با نمادهاي زير نشان
ميدهيم.
)j = (0,1
)i = (1,0
32.
با توجه به نماد گذاري گذشته براي هر بردار ) V=(a1,a2بهدست مي آوريم
:
(a1,a2)=a1 (1,0)+a2 (0,1)=a1 i+ a2 j
33.
بنابر اين هر بردار V2در را مي توان به صورت يك تركيبخطي از دو بردار iو ( jعبارتي به صورت a1 i + a2 jرا يك
تركيب خطي از iو jمي نامند ).نوشت .از اين رو بردارهاي iو j
يك پايه براي فضاي برداري V2تشكيل مي دهند .تعداد عناصر
يك پايه يك فضاي برداري ،بعد فضاي برداري نام دارد.
بنابر اين V2يك فضاي برداري دو بعدي است.
34. 1.1.25 تعريف توازي بردارها
1.1.25تعريف توازي بردارهادو بردار نا صفر Uو Vرا موازي مي ناميم ،در صورتي كه
اسكالر (عدد حقيقي ) cوجود داشته باشد ،به طوري
كه . V=cU
35. 1.1.25 قضيه
1.1.25قضيهاگر Vبردار نا صفري باشد ،آنگاه
V
1
v
=U
بردار يكه ( واحد) هم جهت با Vاست
.
36. 1.2 ضرب عددي دو بردار
1.2ضرب عددي دو بردار37. 1.2.1 تعريف ضرب عددي دو بردار
1.2.1تعريف ضرب عددي دو برداراگر ) U=(a1,a2و) V=(b1,b2دو بردار در V2باشند ،
آنگاه حاصلضرب عددي دو بردار Uو Vرا با U.Vنشان
مي دهيم و به صورت زير تعريف مي كنيم:
U.V=(a1,a2).(b1,b2)=a1 b1+a2 b2
38.
توجه مي كنيم كه حاصلضرب عددي دو بردار ،عدديحقيقي است و بردار نيست .اين حاصلضرب داخلي يا
حاصلضرب نقطه اي دو بردار نيز ناميده مي شود.
39. 1.2.4 قضيه
1.2.4قضيهاگر Uو Vو Wبردارهايي در V2بوده و cيك اسكالر باشد.
آنگاه:
U.V=V.U
.1
U.(V+W)=U.V+U.W
.2
(U+V).W=U.W+V.W
.3
)c(U.V)=(cU).V=U.(cV
.4
0.U=0
.5
V.V= V
.6
40. 1.2.5 تعريف زاويه ي بين دو بردار
1.2.5تعريف زاويه ي بين دو بردارفرض مي كنيم Uو Vدو بردار نا صفر باشند به
طوري Uكه مضرب اسكالري از Vنباشد.اگر OPوOQ
به ترتيب بردارهاي نمايشگر Uو Vباشند.آنگاه زاويه ي
بين Uو Vرا كوچكترين زاويه ي بين دو پاره خط OP
و OQتعريف مي كنيم.
41.
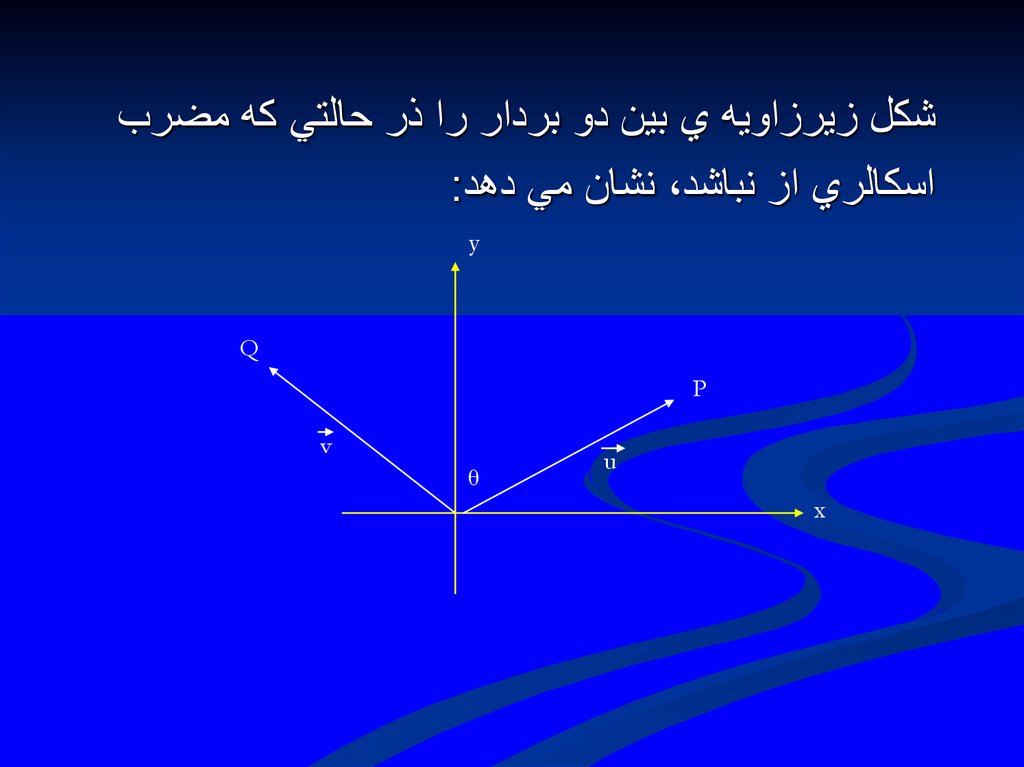
شكل زيرزاويه ي بين دو بردار را ذر حالتي كه مضرباسكالري از نباشد ،نشان مي دهد:
y
Q
P
u
x
v
θ
42. 1.2.6 قضيه
1.2.6قضيهاگر θزاويه ي بين دو بردار Uو Vباشد،آنگاه:
U.V= U V cos θ
43. 1.2.8 نتيجه
1.2.8نتيجهاز قضيه ي قبل نتيجه مي شود كه دو بردار Uو Vبر هم
عمودند ( متعامدند) اگر و تنها اگر:
U.V=0
44. 1.2.10 تصوير يك بردار بر روي بردار ديگر
1.2.10تصوير يك بردار بر روي بردار ديگرفرض مي كنيم OPو OQبه ترتيب نمايشگرهاي بردارهاي
Uو Vباشند.تصوير OQدر جهت ،OPبردار ORاست،كه
در آن Rپاي عمود از نقطه Qي بر خطي است كه از دو
نقطه ي كه از دو نقطه Dو Pمي گذرد.
45.
شكل :تصوير بردار Vبر روي بردارPy
Q
p
v
u
x
R
θ
o
46. 1.2.11 تعريف
1.2.11تعريفاگر Uبردار ناصفري باشد ،تصوير برداري Vروي بردارU
به صورت زير تعريف مي كنيم:
u
U.V
2
U
v
= Proj u
47.
تصوير اسكالر Vروي Uبرابر با V cosθاست .با توجهبه قضيه داريم:
)
U
U
(=V.
V.U
U
= V cosθ
48. 1.3 بردارها در فضاي سه بعدي
1.3بردارها در فضاي سه بعدي49. 1.3.1 تعريف
1.3.1تعريفمجمو عه ي تمام سه تايي هاي مرتب از اعداد حقيقي را
فضاي عددي سه بعدي مي ناميم و با Rنشان مي دهيم.
هر سه تايي مرتب ( zو yو )xرا يك نقطه در فضاي عددي
سه بعدي مي ناميم.
50. 1.3.2 قضيه
1.3.2قضيهفاصله ي بين دو نقطه ( zو yو p)xو ( zو yو p)xبرابر
1 1 1
2 2 2
است با:
) pp = (x –x )+(y –y )+(z –z
1
2
1
2
1
2
1 2
51. 1.3.4 تعريف
1.3.4تعريفيك بردار در فضاي سه بعدي ،يك سه تايي مرتب از اعداد
حقيقي به صورت (2 a 3و aو ) a 1است .اعداد a 2، a 1و a 3را
مولفه هاي بردار ( aو aو )aمي ناميم .مجموعه تمام
1
2 3
بردارهايي به صورت ( aو aو) aرا با V3نشان مي
1
2
3
دهيم.
52.
اگر بردارهاي يكه iو jو kعبارت باشند از:)k=(0,0,1
)j=(0,1,0
)i=(1,0,0
آنگاه هر بردار ( V=(a1,a2,a3در V3را مي توان به صورت
زير نوشت:
V=(a1,a2,a3)=a1 i+ a2 j+ a3 k
53. 1.3.5 تعريف
1.3.5تعريفسه زاويه ي αو βو δزوايايي كه بردار Vنا صفر به ترتيب
با جهت مثبت محورهاي xو yو zمي سازد را زواياي
هادي Vمي ناميم.توجه كنيد كه هر زاويه ي هادي بزرگتر
يا مساوي 0و كوچكتر يا مساوي пاست.
54.
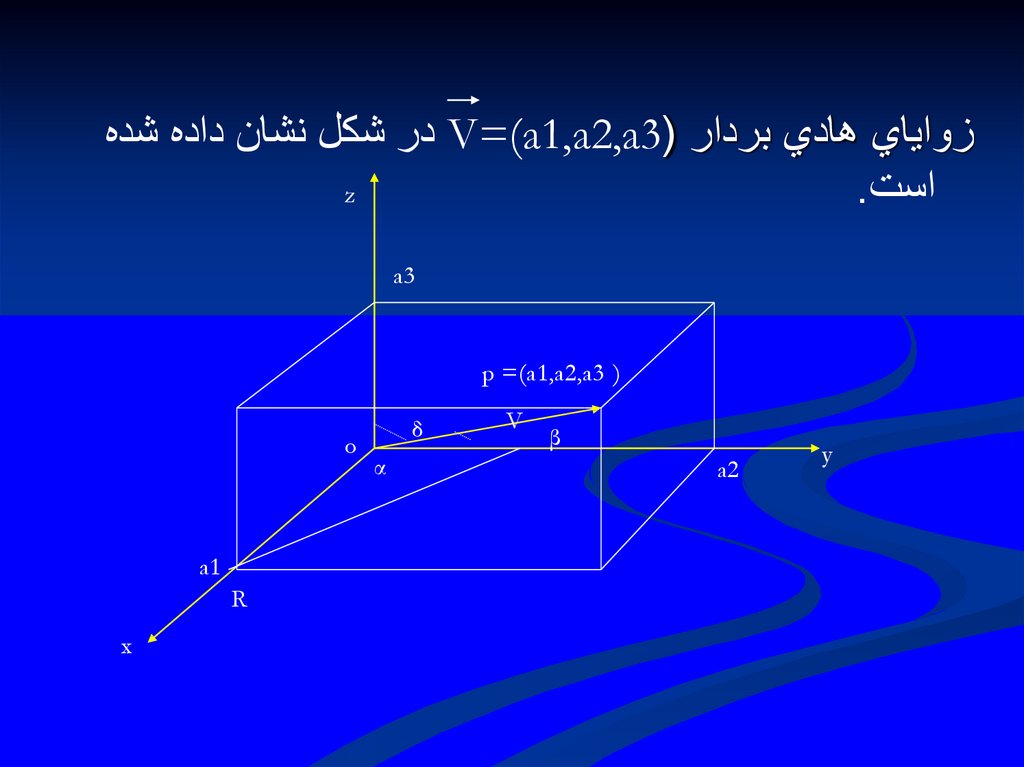
زواياي هادي بردار ( V=(a1,a2,a3در شكل نشان داده شدهz
است.
a3
) p =(a1,a2,a3
y
β
a2
V
δ
α
o
a1
R
x
55.
در شكل مؤلفه هاي Vاعدادي مثبت و زواياي هادي آن مثبتو كوچكتر п/2از هستند.به طوري كه در شكل ديده مي
شود ،مثلث قايم الزاويه OPRاست و داريم :
a1
V
=
OR
OP
=COSα
56.
مي توان نشاشن داد كه دستور اخير به ازاي п/2 ≤α≤ пنيز بر قرار است.دستور هاي مشابهي براي COSβو
COS αبه دست مي آيند.
a3
V
= COS α
a2
V
= COSβ
57.
اعداد COS αو COSβو COS δراكسينوسهاي هاديبردار Vمي نامند.
توجه كنيد كه بردار صفر ،زواياي هادي و در نتيجه كسينوس
هاي هادي ندارد.
58. 1.3.7 نكته
1.3.7نكتهاگر اندازه ي يك بردار و كسينوسهاي هادي آن معلوم
باشند،آنگاه بردار به طور منحصر به فردي معي است،
زيرا:
a1= COS α V
a2= COSβ V
a3= COS δ V
59. 1.3.8 قضيه
1.3.8قضيهاگر COS αو COSβو COS δكسينوسهاي هادي بردار
Vباشند،آنگاه:
2
2
COSβ + COS δ = 1
2
COS α +
60. 1.3.15 نتيجه
1.3.15نتيجهاز قضيه و تعريف كسينوسهاي هادي نتيجه مي شمد كه مؤلفه
هاي يك بردار يكه كسينوسهاي هادي آن هستند.
61.
به عبارت ديگر اگر ( V=(a1,a2,a3بردار يكه هم جهت با Vباشد آنگاه:
62.
در مورد بردارهاي فضايي اعمال جمع ،تفريق،ضرب اسكالرو ضرب عددي دو بردار در، V3مشابه آنچه V2در
تعريف مي شوند.
فرض مي كنيم ) U=(a1,a2,a3و ) V=(b1,b2,b3يك اسكالر
باشد.داريم:
63.
الفب
64.
پت
65. 1.3.14نكته
1.3.14نكتهبه آساني مي توان نشان داد كه:
1
0
66. 1.3.15قضيه
1.3.15قضيهاگر θزاويه ي بين دو بردار نا صفر Uو Vدر V3باشد آنگاه:
67. 1.3.16تعريف
1.3.16تعريفدو بردار در V3را موازي مي ناميم اگر و تنها اگر يكي از
بردارها مضرب اسكالري از ديگري باشد.
68. 1.3.17قضيه
1.3.17قضيهدو بردار نا صفر در V3موازي اند اگر و تنها اگر زاويه ي
بين آنها 0يا пباشد.
69. 1.3.18قضيه
1.3.18قضيهدو بردار نا صفر Uو Vدر V3متعامدند اگر و تنها اگر
U.V=0
70.
1.4ضرب برداري بردارها71. 1.4.1تعريف
1.4.1تعريفاگر ) U=(a1,a2,a3و ) V=(b1,b2,b3آنگاه حاصل ضرب
برداري Uدر Vبا نشان U*Vمي دهيم.برداري است كه به
صورت زير تعريف مي شود:
)U*V=(a2b3-a3b2,a3b1-a1b3,a1b2-a2b1
72.
براي سهولت در يادگيري و به ذهن سپردن دستور ، U*Vازنماددترمينين استفاده مي كنيم.يك دترمينان مرتبه ي دوم را
به صورت زير تعريف مي كنيم:
73.
با استفاده از نماد دترمينان دستور محاسبه ي U*Vبهصورت زير در مي آيد:
74.
سمت راست عبارت اخير را مي توان با نماد زير نشان داد:75. 1.4.3قضيه
1.4.3قضيهاگر Uو Vبردارهايي در V3باشند ،آنگاه:
)U*V= - (V*U
76. 1.4.4قضيه
1.4.4قضيهاگر iو jو kبردارهاي يكه ي V3باشند ،آنگاه:
77. 1.4.5قضيه
1.4.5قضيهاگر Uو Vو Wبردارهايي در V3و cيك اسكالر باشد آنگاه:
78. 1.4.7قضيه
1.4.7قضيهاگر Uو Vدو بردار V3و θزاويه ي بين Uو Vباشد،آنگاه:
U*V = U V sinθ
79. 1.4.9نتيجه
1.4.9نتيجهاگر Uو Vدو بردار نا صفر در V3باشند آنگاه و موازي اند
اگر و تنها اگر U*V=0
80. 1.4.11قضيه
1.4.11قضيهاگر Uو Vو Wسه بردار در V3باشند ،آنگاه:
81. 1.4.12تعريف
1.4.12تعريففرض مي كنيم ) U=(a1,a2,a3و )V=(b1,b2,b3و
) . W =(c1,c2,c3حاصلضرب ) U.(V*Wرا
حاصلضرب عددي سه گانه بردارهاي Uو Vو Wمي
ناميم.
82.
حاصلضرب عددي سه گانه برابر است با:83.
حاصلضرب عددي سه گانه يك اسكالر است.84. 1.4.13قضيه
1.4.13قضيهاگر Uو Vدو بردار نا صفر در باشند آنگاه:
85.
1.5بردارهاي فضاي nبعدي86. 1.5.1تعريف
1.5.1تعريففرض كنيد nعدد صحيح مثبتي باشد n ،تايي مرتب
)(x1,x2…,xnمجموعه اي از nعدد است كه به ترتيب
معيني نوشته شده اند.
87.
اعداد حقيقي xn,……,x2,x1را به ترتيب مؤلفه هاي اول تاnام اين nتايي مرتب مي خوانيم.مجموغه ي تمام nتايي
n
هاي مرتب را با Rنشان مي دهيم.
88.
دو تايي مرتب) Y=(y1,y2,…ynو) X=(x1,x2,…xnرابرابر مب ناميم اگر و تنها اگر براي هر i=1,2,…nداشته
باشيم:
xi=yi
89. 1.5.3تعريف
1.5.3تعريففرض مي كنيم) U=(a1,a2,…anو) V=(b1,b2,…bnدو
بردار در Vnو cعدد حقيقي (اسكالر) باشد.
90.
مجموع دو بردار و ضرب اسكالر عدد در بردار به صورتزير تعزيف مي شود:
)U+V=(a1+b1,a2+b2,…,an+bn
)cU=(ca1,ca2,…,can
91. 1.5.4قضيه
1.5.4قضيهفرض مي كنيم Uو Vو Wسه بردار در Vnو cو kدو
اسكالر (عدد حقيقي) باشند .در اين صورت
الف)جمع بردارها جا به جايي پذير است ،يعني
U+V=V+U
92.
ب) جمع بردارها شركت پذير است ،يعني)(U+V)+W=U+(V+W
پ)عمل جمع داراي عضو خنثي است يعني
بردار) 0=(0,0,…,0بردار صفر nمؤلفه اي وجود دارد به
طوري كه
U+0=U
93.
ت) براي هر Uبردار قرينه –Uوجود دارا به طوري كهU+(-U)=0
c (U+V)=c U +c V
ث)
)(c k) U=c (k U
ج)
(c+ k) U=c U +k U
ح)
خ)وجود هماني نسبت به ضرب اسكالر،يعني
1U=U
94. 1.5.5تعريف
1.5.5تعريفطول بردار ) U=(a1,a2,…anبرابر است با
95. فصل دوم:ماتريس و دترمينان
فصل دوم:ماتريس و دترمينان96.
در اين فصل با معرفي ماتريس مفهوم بردار را تعميم ميدهيم.همچنين انواع ماتريس،ماتريسهاي خاص و اعمال
جبري روي ماتريس ها ،دترمينين و وارون ماتريس را
مورد مطالعه قرار مي دهيم.
97. 2.1ماتريس
2.1ماتريس98. 2.1.1تعريف
2.1.1تعريفهر جدولي از اعداد را كه شامل mسطر و nستون باشد،يك
ماتريس mدر nمي ناميم و به شكل زير نشان مي دهيم.
يا
99.
هر يك از اعداد aijرا يك عنصر يا درايه ماتريس ميناميم.در اينجا iانديس سطر و jانديس ستون است،به بيان
ديگر ،عنصر aijدر محل تالقي سطر iام و ستون jام
ماتريس قرار دارد.
100. 2.1.2تعريف
2.1.2تعريفالف)هر گاه ماتريس A=(aij)mnتنها داراي يك سطر
باشد،يعني ، m=1اين ماتريس را يك ماتريس سطري
(بردار سطري)مي ناميم.
ماتزيس [1و4و ]-3يك ماتريس سطري است.
101.
اگر ماتريس A=(aij)mnتنها داراي يك ستون باشد.يعني،n=1اين ماتريس را يك ماتريس ستوني (بردار ستوني)مي
ناميم.
يك ماتريس ستوني است.
ماتريس
102.
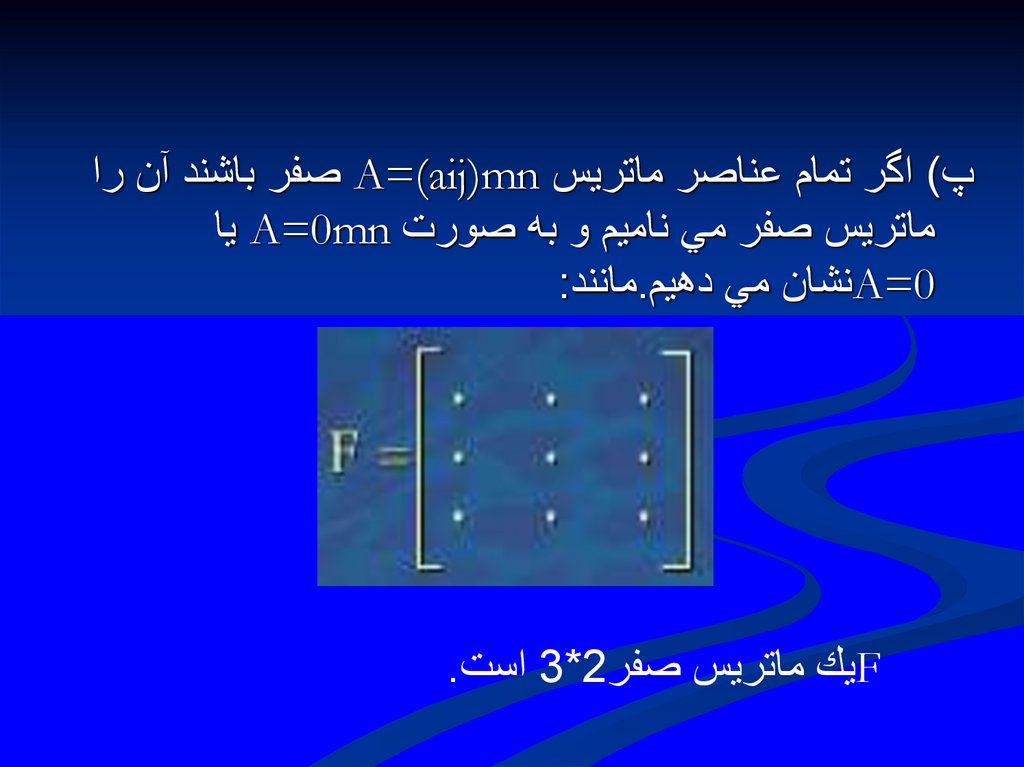
پ) اگر تمام عناصر ماتريس A=(aij)mnصفر باشند آن راماتريس صفر مي ناميم و به صورت A=0mnيا
A=0نشان مي دهيم.مانند:
Fيك ماتريس صفر 3*2است.
103. 2.1.3تعريف
2.1.3تعريفماتريسي را كه تعداد سطرها و تعداد ستونهايش برابر باشد،
يك ماتريس مربع مي ناميم.به بيان ديگر A=(aij)mnيك
ماتريس مربع است اگر و تنها اگرm=n
104.
در ماتريس مربع ، A=(aij)mnقطري را كه شامل عناصر a11,a22,…,annقطر اصلي و اين عناصر را عناصر
قطر اصلي مي ناميم.
105.
106. 2.1.4تعريف
2.1.4تعريفماتريس مربع A=(aij)mnرا يك ماتريس هماني يا واحدn*n
مي ناميم اگر هر يك از عناصر قطر اصلي برابر 1و همه
ي عناصر ديگر آن صفر باشند.
107.
ماتريس واحد n*nرا با Iنشان مي دهيم .مانند:108. 2.1.5تعريف تساوي دو ماتريس
2.1.5تعريف تساوي دو ماتريسدو ماتريس A=(aij)mnو B=(bij)pqرا برابر مي گوييم
اگر m=pو n=qو براي هر iوj
كهi=1,2,…mو j=1,2,…nداشته باشيم aij=bij
109.
براي مثال:110. 2.1.7تعريف
2.1.7تعريففرض مي كنيم A=(aij)mnو B=(bij)mnدو ماتريس
m*nو kعددي حقيقي باشد.
111.
الف) حاصل جمع اين دو ماتريس را با A+Bنشان داده و بهصورت زير تعريف مي كنيم:
112.
ب)حاصل ضرب عدد حقيقي kدر Aماتريس را با kAنشانداده و به صورت زير تعريف مي كنيم:
113.
توجه كنيد كه A+Bو kAماتريسهاي m*nهستند.توجهداشته باشيد كه جمع دو ماتريس كه داراي تعداد سطرهاي
متفاوت يا تعداد ستونهاي متفاوت باشند تعريف نشده است.
114. 2.1.9تعريف
2.1.9تعريفاگر A=(aij)m0ماتريس )-1( Aرا قرينه ي ماتريس Aمي
ناميم و با – A=(-aij)m0نشان مي دهيم.
اگر A=(aij)mnو B=(bij)mnبنابر تعريف داريم:
)A-B=A+(-B
115. 2.1.11قضيه
2.1.11قضيهاگر Aو Bو Cسه ماتريس m*nو kو hدو عدد حقيقي باشند
آنگاه:
116. 2.1.13تعريف
2.1.13تعريفماتريسهاي A=(aij)mpو B=(bij)pnرا در نظر مي
كيريم.منظور از حاصل ضرب Aدر Bماتريس m*nاي
چون cبه طوري كه
حاصل ضرب Aدر Bيعني cرا با ABنشان مي دهيم.
117. 2.1.15قضيه
2.1.15قضيهاگر A=(aij)mnيك ماتريس مربعي n*nباشد آنگاه:
118. 2.1.16قضيه
قضيه2.1.16 آنگاهC=(cij)qn وB=(bij)pq وA=(aij)mp اگر
A(BC)=(AB)C
119. 2.1.19قضيه
قضيه2.1.19C=(cij)mp وB=(bij)pn وA=(aij)pn اگر
C(A+B)=CA+CB
120. 2.1.20تعريف
2.1.20تعريفاگر در ماتريس A=(aij)mnجاي سطرها و ستونها را با
يكديگر عوض كنيم ،ماتريس حاصل را
T
ترانهاده) (Transposeماتريس Aمي ناميم و آن را با A
T
نشان مي دهيم .به بيان ديگر A=(bij)nmكه در آن برايi
و jداريم:
bij=aij
121. 2.1.21قضيه
2.1.21قضيهاگر Aو Bدو ماتريسm*nو kعددي حقيقي باشد آنكاه:
TT
الف) (A)=Aيعني ترانهاده ،ترانهاده ماتريس با ماتريس
برابر است.
T
T
ب)) (kA)=k(Aيعني ترانهاده مضربي از يك ماتريس با
همان مضرب ترانهاده ماتريس بربار است.
122.
TT
T
پ) ،(A+B) = A+ Bيعني ترانهاده مجموع دوماتريس با
مجموع ترانهاده هاي دو ماتريس برابر است.
T
T T
ت) اگر Aو Bدو ماتريس مربع باشند،آنگاه (AB)=B A
،يعني ترانهاده ي حاصلضرب دو ماتريس با حاصلضرب
ترانهاده ماتريس دومي در ترانهاده ماتريس اولي برابر
است.
123. 2.1.23تعريف
2.1.23تعريفT
الف) ماتريس مربع Aرا متقارن مي ناميم اگر . A =A
براي مثال ماتريس زير متقارن است .توجه كنيد كه در
ماتزيس متقارن عناصر ماتريس نسبت به قطر اصلي
متقارن هستند.
124.
ب) ماتريس Aمربع را شبه متقارن مي ناميم اگر. A=ATاگر يك ماتريس شبه متقارن باشد بايد براي هر iو jداشته
باشيم aij=-aijاما از aii=-aiiنتيجه مي شود . aii=0پس
عناصر قطر اصلي در ماتريس شبه متقارن همگي برابر
صفرند.
125.
پ) ماتريس Aمربع را قطري مي ناميم اگر همه ي عناصرغير واقع بر قطر اصلي آن صفر باشند.مانند:
126.
ت) ماتريس قطري Sرا يك ماتريس اسكالر مي ناميم ،اگرعناصر قطر اصلي آن برابر عدد ثابت Kباشد ،يعني
127.
ث) ماتريس n*nو cرا متعامد مي گوييم اگر :128.
براي مثال:آنگاه
پس cماتريسي متعامد است.
129.
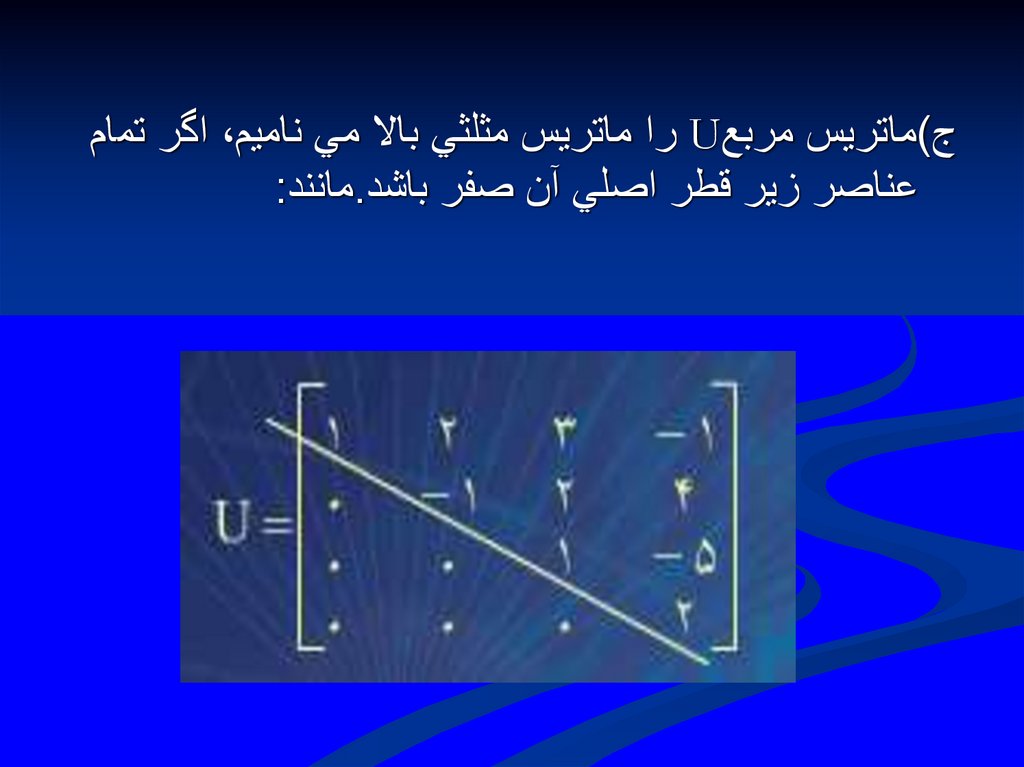
ج)ماتريس مربع Uرا ماتريس مثلثي باال مي ناميم ،اگر تمامعناصر زير قطر اصلي آن صفر باشد.مانند:
130.
چ)ماتريس مربع Lرا ماتريس مثلثي پايين مي ناميم ،اگر تمامعناصر باالي قطر اصلي آن صفر باشد.مانند:
131. 2.1.25تعريف
2.1.25تعريفدر ماتريس مربع A=(aij)nnمجموع تمام قطر اصلي را اثر
Aمي ناميم و با ) tr(Aنشان مي دهيم.پس:
132.
2.2دترمينان133.
دترمينان ماتريس Aرا با det Aيا Aنشان مي دهيم.134. 2.2.1تعريف
2.2.1تعريف )1ماتريس 1*1تنها داراي يك عنصر a11است ،دترمينان
اين ماتريس را برابر با عدد a11تعريف مي كنيم.
135.
)2دترمينان ماتريس 2*2به صورت زير تعريف مي شود
a11 a12
= a11a22-a12a21
a22
a21
= Det A= A
136. 2.2.2تعريف
2.2.2تعريفماتريس A=(aij)nnرا در نظر مي گيريم .فرض كنيد Mij
ماتريسي ) (n-1)*(n-1باشد كه از حذف سطر iام و ستون jام
ماتريس Aبه دست آمده است .دترمينان ماتريس ،Mijيعني
Mijرا مينور عنصر در ماتريس مي ناميم.
137. 2.2.3تعريف
2.2.3تعريفهمسازه عنصر aijدر ماتريس A=(aij)nnرا با Aijنشان
مي دهيم وبرابر با عدد زير است:
138. 2.2.4تعريف
2.2.4تعريفدترمينان ماتريس A=(aij)nnرا به صورت
تعريف مي كنيم.مي گوييم دترمينيان Aبر حسب سطر iام
بسط داده شده است.
139.
بنابر اين تعريف براي محاسبه ي دترمينان يك ماتريس ،يكسطر يا يك ستون را انتخاب مي كنيم .اين سطر يا ستون
را در همسازه اش ضرب ،سپس مقادير حاصل را با هم
جمع مي كنيم.
140.
اگر دترمينان را بر حسب سطر يا ستوني كه بيشترين تعدادصفر را دارد محاسبه مي كنيم ،محاسبات كوتاهتر مي
شود ،زيرا نيازي به محاسبه ي همسازه هاي صفر
نيست.چون حاصلضرب صفر در هر همسازه اي صفر
است.
141. 2.2.7قضيه(خواص دترمينان)
2.2.7قضيه(خواص دترمينان) )1دترمينان ماتريس مربع Aو ترانهاده Aبرابر است
.يعني:
T
A =A
)2اگر تمام عناصر يك سطر يا يك ستون ماتريس Aصفر
باشند ،آنگاه
A =0
142.
)3اگر تمام عناصر يك سطر يا يك ستون ماتريس Aدرعدد rضرب مي كنيم آنگاه دترمينان ماتريس حاصل برابر
با r Aاست.
)4دترمينان ماتريس حاصل از تعويض دو سطر يا دو ستون
ماتريس Aمساوي است با منهاي دترمينان .A
143.
)5اگر دو سطر يا دو ستون ماتريسي برابر باشند ،آنگاهمقدار دترمينان آن برابر با صفر است.
)6دترمينان حاصل از جمع مضرب اسكالري از يك سطر (يا
ستون) با سطري ( يا ستوني) ديگر از ماتريس Aمساوي
است با دترمينان .A
144.
)7دترمينان حاصلضرب دو ماتريس برابر با حاصلضربدترمينانهاي آنها است يعني
AB = A B
)8دترمينان يك ماتريس قطري برابر است با حاصلضرب
عناصر روي قطر اصلي آن.
)9دترمينان ماتريس واحد برابر يك است ،يعني
In = 1
145. 2.2.15تعريف
2.2.15تعريفاگر دترمينان ماتريس A=(aij)nnبرابر صفر باشد ،ماتريس
Aرا منفرد مي ناميم .در غير اين صورت ماتريس را غير
منفرد مي ناميم.
ماتريس زير منفرد است.
146. 2.3وارون ماتريس
2.3وارون ماتريس147. 2.3.1تعريف
2.3.1تعريفماتريس A=(aij)nnرا وارون پذير مي ناميم ،اگر ماتريسي
مانند B=(bij)nnوجود داشته باشد به طوري كه
AB=BA=In
اگر Aماتريسي وارون پذير باشد ،آنگاه وارون آن منحصر به
-1
فرد است و آن را با Aنشان مي دهيم.
148. 2.3.5اعمال سطري مقدماتي
2.3.5اعمال سطري مقدماتيماتريس A=(aij)nnرا در نظر مي كيريم .هر يك از اعمال
زير را كه بر روي سطر هاي ماتريس Aانجام مي پذيرد،
يك عمل سطري مقدماتي مي ناميم.
)1تعويض دو سطر ماتريس .A
)2ضرب يك سطر ماتريس Aدر يك عدد نا صفر.
)3افزودن مضربي از يك سطر ماتريس Aبه سطري ديگر.
149.
براي اختصار در نوشتن اعمال سطري مقدماتي ،از حرفR ،اول كلمه ي Rowبه معناي سطر به صورت زير استفاده
مي كنيم.
الف) Ri Rjبه معناي تعويض سطر iام و سطر jام
ب) kR1به معناي ضرب سطر iام ماتريس در عدد ناصفرk
پ) Rj+kRiبه معناي افزودن برابر سطر ام به سطر ام
150. 2.3.8قضيه
2.3.8قضيهاگر ماتريس وارون پذير Aبه وسيله ي يك سلسله اعمال
مقدماتي تبديل به ماتريس واحد شود ،آنگاه با انجام همين
سلسله اعمال سطري مقدماتي بر روي ماتريس واحد ،
وارون ماتريس Aبه دست مي آيد.
151.
براي به دست آوردن وارون ماتريس Aمعموال اعمال سطريمقدماتي را به طور هم زمان بر روي ماتريس Aو
ماتريس واحد انجام مي دهند.لذا ماتريس مركب] [A Iرا
در نظر گرفته و با انجام يك سلسله اعمال مقدماتي سطري
آن را تبديل به ] [I Bميكنيم.بنا بر قضيه ي باال ،برابر
وارون ماتريس است.
152. 2.3.11تعريف
2.3.11تعريفترانهاده ماتريس همسازه هاي ماتريس مربع Aرا ماتريس
الحاقي Aمي ناميم و با نشان مي دهيم ،پس:
153. 2.3.13قضيه
2.3.13قضيهاگر Aيك ماتريس n*nباشد آنگاه :
154. 2.3.13قضيه
2.3.13قضيهاگر، detA=0آنگاه وارون وجود دارد و برابر است با
عكس اين نتيجه نيز درست است.يعني اگر Aوارون پذير باشد
،آنگاه
155. 2.3.17قضيه
2.3.17قضيهاگر Aو Bدو ماتريس مربع n*nو وارون پذير باشند آنگاه
الف) ماتريس حاصلضرب وارون پذير است و
ب) ماتريس ترانهاده Aوارون پذير است و
156.
پ) وارون ماتريس وارون Aبرابر Aاست ،يعنيت) دترمينان وارون ماتريس Aبرابر با معكوس دترمينان A
است يعني
157. فصل سوم: دستگاه معادلات خطي و توابع خطي
فصل سوم :دستگاه معادالت خطي و توابع خطي158.
در اين فصل با استفاده از مفهوم ماتريس و دترمينان روشيبراي حل و بحث در وجود جوابهاي دستگاه معادالت خطي
ارائه دهيم .سپس استقالال و وابستگي خطي يك مجموعه از
بردارها را مورد بررسي قرار دهيم .در خاتمه ي فصل با
توابع خطي آشنا مي شويم.
159. 3.1دستگاه معادلات خطي
3.1دستگاه معادالت خطي160.
معادله اي به صورت a1x1+a2x2+…+anxn=0بامجهول xn,…,x2,x1را يك معادله ي nمجهولي خطي
مي ناميم n .تايي ) (x1,x2,…,xnاز اعداد حقيقي را كه در
اين معادله صدق كنند يك جواب آن مي ناميم.
161. 3.1.1تعريف
3.1.1تعريفمجموعه اي از معادالت خطي
را يك دستگاه mمعادله ي خطي nمجهولي مي ناميم.
162.
تايي از اعداد حقيقي را در تمام معادله هاي دستگاه صدق كنديك جواب اين دستگاه مي ناميم.
163.
اين دستگاه را ميتوان به صورت معادله ي ماتريسي زيرنوشت:
164.
با فرضمعادله ي ماتريسي اخير به صورت خالصه ي زير در مي
AX=B
آيد.
Aرا ماتريس ضرايب Xرا ماتريس مجهولها و Bرا ماتريس
طرف دوم دستگاه معادالت خطي مي ناميم.
165.
توجه كنيد يك دستگاه معادالت خطي ممكن است داراي يكجواب منحصر به فرد يا بينهايت جواب باشد ويا اصال
جوابي نداشته باشد.
166.
اينك به معرفي روشهايي براي حل يك دستگاه معادالت خطيمي پردازيم.
-1روش حذف گوسي
-2دستور كرامر
167. 3.1.2روش حذف گوسي
3.1.2روش حذف گوسيميتوان نشان داد دو دستگاه معادالت خطي كه يكي از آنها به
وسيله ي انجام اعمال زير روي معادالت دستگاه ديگري به
دست آمده باشد داراي جواب يا جوابهاي يكسان هستند:
168.
(1(2
(3
ضرب يك معادله ي دستگاه در عددي غير صفر.
تعويض محل دو معادله ي دستگاه و
افزودن مضربي از يك معادله به معادله ي ديكر دستگاه.
169.
پس براي حل دستكاه AX=Bبايد تا جايي كه ممكن است بهوسيله ي اعمال سطري مقدماتي ماتريس ] [A Bرا به
ماتريس ساده تري تبديل كنيم تا جوابها به آساني به دست
آيند.
170. 3.1.6قضيه
3.1.6قضيهاگر تعداد مجهولها با تعداد معادله ها ي يك دستگاه معادالت
خطي برابر باشد (دستگاه nمعادالت nمجهولي) و
ماتريس ضرايب دستگاه وارون پذير باشد آنگاه دستگاه
همواره داراي يك جواب منحصر به فرد است.
171. 3.1.8دستور كرامر
3.1.8دستور كرامراگر ضرايب يك دستگاه nمعادالت nمجهولي وارون پذير
باشد آنگاه جواب دستگاه برابر است با
كه درآن Aiماتريس حاصل از جايگزين كردن
در ستون iام ماتريس Aاست.
ماتريس ستوني
فرمول * را دستور كرامر مي ناميم.
172. 3.1.10تعريف
3.1.10تعريفاكر در دستگاه mمعادله ي nخطي مجهولي طرف دوم تمام
معادالت صفر باشند دستگاه را همگن مي ناميم .در غير
اين صورت دستگاه را غير همگن مي ناميم.
173.
روشن است كه در دستگاه همگنهمواره x1=x2=…=xn=0يك جواب دستگاه هست .اين
جواب به جواب بديهي دستگاه موسوم است.
174. 3.1.11قضيه
3.1.11قضيهدستكاه nمعادله ي خطي nمجهولي همگن داراي يك جواب
غير بديهي ( غير صفر) است .اگر و تنها اگر دترمينان
ضرايب دستگاه صفر باشد.
175. 3.1.13نتيجه
3.1.13نتيجهيك دستگاه mمعادله ي nخطي مجهولي همگن همواره
داراي يك جواب غير بديهي ( غير صفر) است اگر
m<n
176. 3.1.15قضيه
3.1.15قضيهاگر X1و X2دو جواب دستگاه غير همگن AX=Bباشند
آنگاه X2-X1جوابي براي دستگاه همگن AX=0است.
177. 3.1.13نتيجه
3.1.13نتيجهدستگاه غير همگن AX=Bداراي يك جواب منحصر به فرد
است اگر و تنها اگر جواب AX=0منحصر به فرد باشد.
178. 3.2استقلال و وابستگي خطي
3.2استقالل و وابستگي خطي179. 3.2.1تعريف
3.2.1تعريفمجموعه ي mبردار} {V1,V2,…,Vnاز عناصر فضاي
برداري Rرا مستقل خطي مي ناميم اگر هيچ مجمو عه اي
از اعداد حقيقي c1,c2,…,cnبه
جز c1=c2=…=cm=0وجود نداشته باشد به طوري كه
180.
به بيان ديگر مجموعه ي mبردار} {V1,V2,…,Vnمستقلخطي است تنها جواب معادله ي
برابر با c1=c2=…=cm=0باشد .در غير اين صورت
اين مجموعه را وابسته ي خطي مي ناميم.
181. 3.3رتبه ي يك ماتريس
3.3رتبه ي يك ماتريس182.
در اين بخش به هر ماتريس عدد صحيح و مثبتي به نام رتبهي ماتريس را نسبت مي دهيم .با استفاده از اين عدد در
مورد جوابهاي دستگاههاي معادالت خطي را بررسي مس
كنيم.
183. 3.3.1تعريف
3.3.1تعريففرض كنيم Aماتريسي m*nباشد .حداكثر تعداد سطرهاي
مستقل خطي ماتريس Aرا رتبه ي ماتريس Aمي ناميم و
با نشان ) r(Aمي دهيم.
184.
به عبارت ديگر اگر R1,R2,…,Rmسطرهاي ماتريس Aباشند رتبه ي aبرابر با حداكثر تعداد بردارهاي مستقل
خطي در مجموعه ي} {R1,R2,…,Rmاست.
185.
يك روش تعيين رتبه ي ماتريس Aاين است كه بزرگترينزير ماتريس مربع Aرا كه دترمينانش مخالف صفر باشد
به دست آوريم ،تعداد سطرهاي اين ماتريس برابر رتبه ي
ماتريس Aاست.
186. 3.3.6خواص رتبه ي ماتريس
3.3.6خواص رتبه ي ماتريسالف) رتبه ي ماتريس واحد Inبرابر با nاست ،يعني:
ب) رتبه ي ماتريس Aبا رتبه ي ترانهاده ي Aبرابر است ،
يعني:
187.
پ) اگر Aماتريس n*nباشد آنگاه r(A)=nاگر و تنهااگر det A=0به بيان ديگر r(A)<nاگر و تنها اگر
. det A=0
ت) رتبه ي حاصلضرب دو ماتريس همواره نابيشتر از
كوچكترين رتبه دو ماتريس است ،يعني:
188. 3.3.7نتيجه
3.3.7نتيجهاينك با استفاده از مفهوم رتبه ي ماتريس به طور خالصه به
بررسي جوابهاي دستگاه معادالت خطي AX=Bدر
حالتهاي مختلف مي پردازيم.
فرض مي كنيم ماتريس ضرايب ، Aباشد m.برابر با تعداد
معادالت و nمساوي با تعداد مجهولهاي دستگاه است .رتبه
ي ماتريس مركب ] [A Bرا با ) r(A Bنشان مي دهيم.
189.
الف) اگر) r(A B)=r(Aآنگاه دستگاه داراي حداقل يك جواباست.
ب) اگر r(A B)=r(A)=nآنگاه دستگاه داراي يك جواب
منحصر به فرد است.
پ) اگر r(A B)=r(A) <nآنگاه دستگاه داراي بي نهايت
جواب و مجمو عه سطر هاي ماتريس Aوابسته ي خطي
است.
ت) اگر ) r(A B)=r(Aآنگاه دستگاه جواب ندارد.
190. 3.4توابع خطي
3.4توابع خطي191.
در اين بخش به مطالعه ي توابع خطي كه توابعي از يكفضاي برداري به فضاي برداري ديگري هستند مي
پردازيم.
192. 3.4.1تعريف
3.4.1تعريفn
m
تابع nمتغيره ي fاز فضاي برداري Rبه فضاي برداري
Rرا كه به ازاي هر عدد حقيقي rو هر دو nتايي
n
از Rدر دو شرط زير صدق مي كند ،يك تابع خطي مي
ناميم.
193. 3.4.3قضيه
3.4.3قضيهn
n
تابع f: R Rخطي است.اگر و تنها اگر هر مؤلفه مقدا رتابع
fدر
به صورت يك تركيب خطي از اعداد
x1,x2,…,xnباشد.
194.
mاز اين قضيه نتيجه مي شود كه اگر R
شد آنگاه اعداد حقيقي
وجود دارند به طوري كه
n
f : Rتابع خطي با
195.
بنا بر اين A=(aij)m*nقرار دادن مقدار تابع خطي fn
را ميتوان به ازاي هر x Rبه صورت ماتريسي
F(x)=Ax
نوشت.ماتريس Aرا يك ماتريس نمايشگر تابع خطي Fميناميم.
196. 3.4.6تعريف
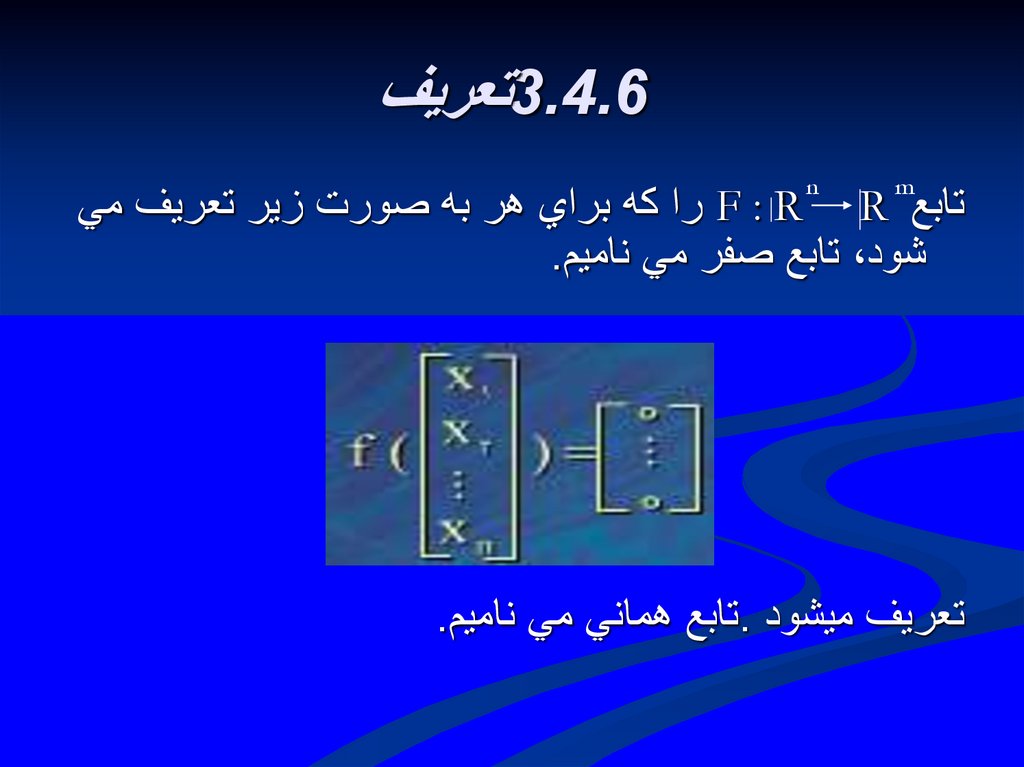
3.4.6تعريفm
n
تابع F : R Rرا كه براي هر به صورت زير تعريف مي
شود ،تابع صفر مي ناميم.
تعريف ميشود .تابع هماني مي ناميم.
197. 3.4.7تعريف
3.4.7تعريفn
تابع R
n
n
I: Rرا كه براي هر X Є Rبه صورت
198. 3.4.8تعريف
3.4.8تعريفm
n
m
n
توابع خطي f : R Rو g : R Rرا در نظر مي گيريم:
(1مجموع fو gرا با f+gنشان ميدهيم و به صورت زير
تعريف مي كنيم:
)(f+g)(x)=f(x)+g(x
)2فرض ميكنيم kعددي حقيقي باشد.حاصلضرب عدد
حقيقي kدر fرا با نشان kfميدهيم و به صورت زير مي
نويسيم.
)(kf)(x)=k f(x
199. فصل چهارم:توابع چند متغيره
فصل چهارم:توابع چند متغيره200.
در فصل هاي قبل با توابعي سر و كار داشتيم كه تنها وابستهبهيك متغير بودند .اين نوع توابع را يك متغيره مي ناميم .ولي
اكثر توابع در اقتصاد و مديريت به بيش از يك متغير
وابسته اند.
201.
فرض كنيد هزينه ي ماهانه ي خانواده اي بستگي به مقدارمصرف آنها از مواد غذايي،پوشاك،خدمات مسكوني و
خدمات بهداشتي و درماني دارد.پس مس توان گفت تابع
هزينه ي اين خانواده يك تابع 4متغيره است.
202. 4.1توابع چند متغيره
4.1توابع چند متغيره203.
nتابع fكه قلمرو آن زير مجموعه اي از Rو برد آن زير
مجموعه اي از اعداد حقيقي باشد.يك تابع nمتغيره مي
ناميم.
204.
اگر fيك تابع nمتغيره باشد هر عنصر قلمرو آن n ،تايي)(x1.x2,…,xnاست ،مقدار تابع به ازاي اين عنصر
قلمرو را با ) f(x1.x2,…,xnنشان مي دهيم.
205. 4.1.3تعريف
4.1.3تعريفn
اگر f,gدو تابع nمتغيره باشند آنگاه براي هر xاز Rو هر
عدد حقيقي ،kاعمال جبري زير تعريف مي شود.
206. 4.2حد و پيوستگي توابع چند متغيره
4.2حد و پيوستگي توابع چندمتغيره
207. 4.2.1تعريف
4.2.1تعريففرض مي كنيم fيك تابع دو متغيره باشد مي گوييم حد تابع
fدر نقطه ي ) (a,bبرابر با Lاست .هنگامي كه نقطه
) (x,yبه نقطه ي ) (a,bنزديك و نزديكتر مي شود
مقدار) f(x,yبه عدد حقيقي Lنزديك و نزديكتر شود .
208.
مي توان نشان داد كه عدد حقيقي Lدر صورت وجودمنحصر به فرد است و لذا Lرا با نماد زير نشان مي دهيم.
209.
حد توابع سه متغيره و به طور كلي nمتغيره نيز به همينصورت تعريف مي شود.تمام مطالبي كه در اين بخش
براي توابع دو متغيره عنوان مي شود براي توابع nمتغيره
نيز درست است.
210. 4.2.2قضيه
4.2.2قضيهاگر f(x,y)=x , g(x,y)=yآنگاه
الف)
211.
ب)اگر k(x,y)=kتابعي ثابت باشد آنگاهLim k(x,y)=k
)(x,y) (a,b
كه در آن kعددي ثابت است.
212. 4.2.3قضيه
4.2.3قضيهاگر حد تابع دو متغيره ي fدر نقطه ي) (a,bبرابر Lباشد
آنگاه
213.
limآنگاه حد تابع ff(x.y)=L
اگر
كه
كند
مي
بيان
قضيه
اين
)(x,y) (a,b
وقتي كه نقطه ي ) (x,yدر مسيرهاي y=bيا x=aبه تقطه
ي ميل كند برابر با Lاست.
214. 4.2.5قضيه
4.2.5قضيهاگر حد تابع fهنگامي ) (x,yكه بر روي دو منحني متمايز به
نقطه ي) (a,bنزديك مي شود متفاوت باشد آنگاه حد تابع f
در اين نقطه وجود ندارد.
215. 4.2.6نتيجه
4.2.6نتيجهاگر
آنگاه تابع fدر نقطه ي ) (a,bحد ندارد.
216.
ابتدا xرا ثابتتوجه كنيد در
را در صورت وجود
فرض كرده
محاسبه مي كنيم.سپس حد عبارت به دست آمده را كه تابعي
از xاست وقتي كه x aپيدا مي كنيم.
217. 4.2.8قضيه
4.2.8قضيهاگر حد توابع دو متغيره ي fو gدر نقطه ي )(a,bاگر حد
توابع دو متغيره ي fو gدر نقطه ي )(a,bوجود داشته باشد
آنگاه
)1حد مجموع دو تابع برابر با مجموع حدهاي آنها است،
يعني:
218.
)2براي هر عدد ثابت k219.
)3حد تفاضل دو تابع برابر با حدهاي آنهاست يععني:220.
)4حد حاصلضرب دو تنبع برابر با حاصلضرب حدهايآنهاست.يعني:
221.
)5حد خارج قسمت دو تابع برابر با خارج قسمت حدهايآنهاست مشروط بر اينكه حد تابع مخرج مخالف صفر باشد،
يعني:
222. 4.2.10قضيه
4.2.10قضيهاگر
باشد آنگاه:
و تابع يك متغيره gدر Lپيوسته
223. 4.2.12تعريف
4.2.12تعريفتابع دو متغيره ي fرا در نقطه ي ) (a,bپيوسته مي ناميم اگر
شرايط زير بر قرار باشد.
)1تابع fدر نقطه ي ) (a,bتعريف شده باشد يعني )(a,b
fمعين باشد.
)2
وجود داشته باشد.
224.
)3در صورتي كه يكي از اين شرايط بر قرار نباشد تابع fرا
در نقطه ي ) (a,bنا پيوسته مي ناميم.
225. 4.2.14قضيه
4.2.14قضيهاگر توابع دو متغيره ي fو gدر نقطه ي ) (a,bپيوسته باشند
(kعددي حقيقي)
آنگاه تواب
(با شرايط )g(a,b)=0نيز در نقطه ي ) (a,bپيوسته اند.
226. 4.2.16قضيه
4.2.16قضيهاگر تابع دو متغيره ي fدر نقطه ي ) (a,bو تابع يك متغيره
ي gدر ) f (a,bپيوسته باشند آنگاه تابع مركب gofدر
نقطه ي ) (a,bپيوسته است.
227. 4.3مشتقهاي جزئي
4.3مشتقهاي جزئي228.
در اين بخش مفهومي نزديك به مفهوم مشتق توابع يك متغيرهرا در مورد توابع چند متغيره ارائه مي دهيم .از اين مفهوم
براي شناخت بهتر توابع چند متغيره استفاده مي كنيم.
229. 4.3.1تعريف
4.3.1تعريففرض مي كنيم fتابعي از دو متغير xو yباشد .اگر
وجود داشته باشد مقدار اين حد را مشتق جزيي fنسبت به
متغير xدر نقطه ي ) (x,yميناميم.و آن را با نمادهاي f
x
(بخوانيد روند ) f (x,yبه
) (x,yيا
روندx
)نشان مي دهيم.
230.
به همين ترتيب مشتق جزيي تابع fنقطه ي) (x,yبه صورت
نسبت به متغير yدر
تعريف مي شود.مشروط بر اينكه اين حد وجود داشته باشد.
231.
اگر ) f x(x,yوجود داشته باشد f xتابعي از دو متغير xو yاستنشان ميدهيم.
اين تابع را به صورت خالصه
نيز به همين ترتيب تعريف مي شود.
تابع
توابع f xو f yرا مشتقهاي جزيي مرتبه ي اول fمي ناميم.
232.
در اينجا نماد ∂ را به جاي dبرتي تمايز مشتقهاي جزيي ازمشتق معمولي به كار مي بريم.
براي محاسبه ي ) f x(x,yدر تابع ) f (x,yمتغير yرا ثابت تلقي
مي كنيم .و از fنسبت به متغير xمانند يك تابع يك متغيره
مشتق مي گيريم.
233.
به همين ترتيب در محاسبه ي ) f x(x,yمتغير را در تابع)f(x,yثابت در نظر گرفته و از fنسبت به متغير yمانند يك تابع
يك متغيره مشتق مي گيريم.
234. 4.3.4مشتقهاي جزيي مرتبه هاي بالاتر
4.3.4مشتقهاي جزيي مرتبه هاي باالترنظير مفهوم مشتقهاي مرتبه هاي باالتر براي توابع يك متغيره
مي توان مشتقهاي جزيي مرتبه هاي باالتررا براي توابع
nمتغيره تعريف كرد .اگر fتابعي از دو متغير xو yباشد
آنگاه f xو f yنيز توابعي از متغيرهاي xو yهستند.پس مي
توان مشتقهاي جزيي توابع fxو fرا تعريف كرد.
y
235.
اين مشتقها را مشتقهاي جزيي مرتبه دوم تابع fمي ناميم.مشتقهاي جزيي مرتبه دوم تابع fعبارتند از:
236.
الزم به تذكر است كه ترتيب نوشتن متغيرهاي xو yدر f x yبر2
خالف ترتيب آنها در نماد
∂ f
∂y ∂x
است.
237. 4.3.6قضيه
4.3.6قضيهفرض مي كنيم fتابعي با متغير هاي xو yباشد .اگر توابع
f xyو f yxدر نقطه ي ) (a,bپيوسته باشد آنگاه:
238. 4.4ديفرانسل كل و مشتقگيري ضمني
4.4ديفرانسل كل و مشتقگيري ضمني239. 4.4.1تعريف
4.4.1تعريففرض مي كنيم fتابعي با متغير هاي xو yباشد .اگر
مشتقهاي جزيي مرتبه اول fوجود داشته باشد ديفرانسيل
كل تابع fرا با نشان dfميدهيم و به صورت زير تعريف
مي كنيم كه در آن dxو dyبه ترتيب ديفرانسيل متغير هاي
xو yاست.
240.
ديفرانسيل كل تابع بيش از دو متغيره نيز به همين ترتيبتعريف مي شود ،اگر uتابعي از چهار متغير z، y ،xوt
باشد آنگاه ديفرانسيل كل تابع برابر است با:
241. 4.4.3نكته
4.4.3نكتهفرض مي كنيم fتابعي با متغير هاي xو yباشد .اگر متغير
هاي xو yنيز توابع يك متغيره ي مشتقپذيري از متغير
ديگري مانند tباشند آنگاه داريم:
242. 4.4.6تعريف
4.4.6تعريففرض مي كنيم fتابعي با متغير هاي xو yباشد .اگر
مشتقهاي جزيي مرتبه ي اول fبر روي ناحيه اي پيوسته
باشد و متغير هاي xو yتوابعي ازمتغير ديگري مانند t
باشند آنگاه مشتق تابع fنسبت به tرا با df/dtنشان مي
دهيم و بنابراين تعريف برابر است با
توجه كنيد كه در واقع fتنها تابعي از متغير tاست.
243. 4.4.8قاعده زنجيري براي توابع چند متغيره
4.4.8قاعده زنجيري براي توابع چند متغيرهفرض مي كنيم fتابعي با متغير هاي xو yباشد .اگر متغير
هاي xو yتوابعي از دو متغيرuو vباشند آنگاه مشتقهاي
جزيي مرتبه ي اول fنسبت به متغير هاي uو vبرابرند
با:
244.
قاعده زنجيري براي توابع بيش از دو متغير كامال مشابهاست.
245. 4.4.10مشتقگيري ضمني
4.4.10مشتقگيري ضمنيبه كمك مفهوم مشتقهاي جزيي مي توان دستور ساده اي براي
مشتقگيري از توابع ضمني ( غير صريح) دو متغيره به
دست آورد.
246.
فرض مي كنيم معادله ي ، f(x,y)=0متغير yرا به صورتتابعي از xبه طور ضمني تعريف كند∂f/ ∂x , ∂f/ ∂y ،
وجود داشته باشند و ∂f/ ∂y =0آنگاه به دست مي آوريم:
247. 4.4.12مشتقهاي جزيي توابع ضمني
4.4.12مشتقهاي جزيي توابع ضمنيفرض مي كنيم تابع دو متغيره ي ) z=f(x,yدر معادله ي
)F(x,y,zصدق كند.پس اگر ∂F/∂x=0آنگاه:
)Fx(x,y,z
)Fz(x,y,z
=-
∂f/ ∂x
∂f/ ∂z
∂z/ ∂x=-
248.
به همين ترتيب به دست مي آوريممشروط بر اينكه ∂F/∂x=0
249. 4.5ماكسيمم و مينيمم توابع دو متغيره
4.5ماكسيمم و مينيمم توابع دو متغيره250.
همهنطور كه از مشتقهاي اول و دوم يك تابع يك متغيره برايتعيين ماكسيمم و مينيمم آن استفاده مي كرديم از مشتقهاي
جزيي مرتبه ي اول و دوم مي توان براي يافتن ماكسيمم و
مينيمم توابع چند متغيره استفاده كنيم.
251. 4.5.1تعريف
4.5.1تعريففرض مي كنيم fتابعي با متغير هاي xو yباشد .در اين
صورت:
الف) ) f(a,bمقدار ماكسيمم (مطلق) fمي ناميم .اگر براي
هر) (x,yاز قلمرو fداشته باشيم:
)F(x,y)<=f(a,b
252.
ب) ) f(a,bمقدارمينيمم (مطلق) fمي ناميم .اگر براي هر)(x,yاز قلمرو fداشته باشيم:
)F(x,y)>=f(a,b
253. 4.5.2تعريف
4.5.2تعريففرض مي كنيم fتابعي با متغير هاي xو yباشد .در اين
صورت:
الف) مي گوييم fتابع در) (a,bداراي يك ماكسيمم نسبي است.
اگر دايره به مركز ) (a,bدر قلمرو fوجود داشته باشد به
طوري كه به ازاي هر) (x,yدر درون اين دايره داشته
باشيم:
)f(x,y)<=f(a,b
254.
ب) مي گوييم fتابع در) (a,bداراي يك مينيمم نسبي است.اگر دايره به مركز ) (a,bدر قلمرو fوجود داشته باشد به
طوري كه به ازاي هر) (x,yدر درون اين دايره داشته
باشيم:
)f(x,y)>=f(a,b
255. 4.5.4قضيه
4.5.4قضيهفرض مي كنيم تابع دو متغيره fدر) (a,bيك ماكسيمم يا مينيمم
نسبي دارد.اگر مشتقهاي جزيي مرتبه ي اول fدر )(a,b
موجود باشند آنگاه:
Fx(a,b)=0
Fy(a,b)=0
256.
از اين قضيه نتيجه مي شود كه اگر تابع fدر) (a,bيك ماكسيمميا مينيمم نسبي داشته باشد آنگاه ) (a,bيك جواب دستگاه دو
مجهولي زير است:
257.
هر جواب اين دستگاه را (نظير توابع يك متغيره ) يك نقطهي بحراني تابع fميناميم.توجه كنيد كه نقطه ي ) (c,dممكن
است يك نقطه ي بحراني fباشد ولي تابع fدر اين نقطه
ماكسيمم و مينيمم نسبي داشته باشد.
258.
اگر ) Fx(a,b)= Fy(a,bولي تابع Fدر( (a,bماكسيمم يامينيمم نسبي نداشته باشد مي گوييم تابع Fدر ( (a,bداراي
يك نقطه ي زين اسبي است.
259.
معموال با استفاده از تعريف تشخيص اينكه يك نقطه ي بحرانيتابع دو دو متغيره ي Fماكسيمم است يا مينيمم مشكل است
.اما به كمك مشتقهاي جزيي مرتبه ي دوم توابع يك يك
متغيره قادر به اين امر هستيم.
260. 4.5.8آزمون مشتق دوم
4.5.8آزمون مشتق دومفرض مي كنيم fتابعي با متغير هاي xو yباشد.و
Fx(a,b)= Fy(a,b)=0همچنين فرض مي كنيم مشتقهاي
جزيي Fدرون دايره اي به مركز( (a,bپبوسته باشند و
261.
در اين صورتالف) اگر ∆ (a,b)>0و Fxx(a,b)<0آنگاه Fدر)(a,bماكسيمم
نسبي دارد.
ب) اگر ∆ (a,b)>0و Fxx(a,b)>0آنگاه Fدر)(a,bمينيمم
نسبي دارد.
262.
پ) اگر ∆ (a,b)>0آنگاه Fدر)(a,bيك نقطه ي زين اسبيدارد .به عبارت ديگر ماكسيمم و مينيمم ندارد.
ت) اگر ∆ (a,b)=0از اين آزمون نتيجه اي به دست نمي آيد.
263.
دقت كنيد كه اگر ∆ (a,b)>0آنگاه حاصلضرب) fxx(a,b)fyy(a,bمثبت است.پس )fxx(a,bو) fyy(a,bهم
عالمت مي باشند .در نتيجه در بندهاي الف و ب آ زمون
مشتق دوم ميتوان ) fyy(a,bرا جايگزين ) fxx(a,bنمود.
264. 4.6ماكسيمم و مينيمم توابع نسبت به شرايط داده شده
4.6ماكسيمم و مينيمم توابع نسبت بهشرايط داده شده
265.
در اكثر مسايل مديريت و اقتصاد تعيين ماكسيمم و مينيمم يكتابع چند متغيره با توجه به يك يا چند شرط صورت مي
گيرد.
266.
براي مثال فرض كنيد هدف يك مصرف كننده به حداكثررسانيدن مطلوب در مصرف دو كاالي 1و 2است .فرض
كنيد قيمت اين دو كاال به ترتيب برابر با p1و p2ميزان
مصرف او از اين دو كاال به ترتيب برابر با x1وx2
باشد.اما اين مصرف كننده محدوديتهايي نيز دارد.
267.
يكي از محدوديتها ميزان درآمد او است .پس مطلوب است اينمصرف كننده تابغي از ميزان استفاده او از اين دو كاال
بوده و ميزان مخارج مصرفي او از اين دو كاال بايد با
ميزان درآمد او نيز برابر باشد.به بيان ديگر ميتوان گفت
كه اين مصرف كننده ميخواهد مطلوبيت خود را با ت.جه
به محدوديت درآمد به حد اكثر برساند.
268.
پس بايد ماكسيمم تابع)U=f(x1,x2
را نسبت به شرط (محدوديت)
P1x1+p2x2=y
پيدا كنيم كه در آن ) U=f(x1,x2تابع مطلوب است.
269.
به دو روش مي توان اين كار را انجام داد .يكي به روشجايگزيني و ديگري به روش الگرانژ .اين دو روش را در
زير معرفي مي كنيم.
270. 4.6.1روش جايگزيني
4.6.1روش جايگزينييكي از روشهاي به دست آوردت ماكسيمم و مينيمم توابع
نسبت به شرايط داده شده از طريق جايگزين كردن تلبع
محدوديت ( شرايط داده شده) در تابع هدف است .بدين
ترتيب مسئله تبديل به مسئله ي ماكسيمم يا مينيمم كردن يك
تابع بدون محدوديت ميشود.
271. 4.6.3روش لاگرانژ
4.6.3روش الگرانژميخواهيم ماكسيمم يا مينيمم تابع دو متغيره ي ) f(x,yرا با
محدوديت g(x,y)=0بيابيم.متغير جديد λموسوم به ضريب
الگرانژ را در نظر مي گيريم با استفاده از متغير λتابع
جديدي به نام تابع الگرانژ را به صورت زير تعريف
ميكنيم.
)F(x,y, λ)=f(x,y)- λg(x,y
272.
پس اگر fدر) (a,bماكسيمم يا مينيمم داشته باشيم آنگاه λ =λ0وجود دارد به طوري كه ) (a,b, λيك جواب دستگاه سه
معادله سه مجهولي زير است.
273. 4.6.5شرط كافي براي وجود ماكسيمم و مينيمم توابع نسبت به شرايط داده شده
4.6.5شرط كافي براي وجود ماكسيمم و مينيممتوابع نسبت به شرايط داده شده
فرض مي كنيم تابع دو متغيره ي ) f(x,yتحت
محدوديت g(x,y)=0داده شده باشد و) F(x,y, λتابع
الگرانژ متناظر باشد .ثابت ميشود كه شرط كافي براي
وجود
274.
الف) ماكسيمم اين است كه275.
ب) مينيمم اين است كه276. 4.6.6نكته
4.6.6نكتهروش الگرانژ را ميتوان براي تابع nمتغيره )f(x1,x2,…,xn
با تابع محدوديت ) i=1,2,…,n gi(x1,x2,…,xnكه در آن
تعميم داد.
277.
در اين صورت تابع الگرانژ عبارتند ازاز مساوي صفر قرار دادن مشتقهاي جزيي تابع الگرانژ
دستگاهي شامل n+kمعادله ي n+kمجهولي به دست مي
آيد.
278. فصل پنجم:معادلات ديفرانسيل
فصل پنجم:معادالت ديفرانسيل279.
حل برخي از مسايل در مديريت ئ اقتصاد منجر به بررسيمعادله اي بين يك تابع مجهول و مشتقهاي آن مي شود.چنين
معادله اي را يك معادله ي ديفرانسيل مي ناميم.در اين فصل
با معرفي چند نوع معادله ي ديفرانسيل ساده روش حل آنها
را مطالعه مي كنيم.
280. 5.1آشنايي با معادلات ديفرانسيل
5.1آشنايي با معادالت ديفرانسيل281. 5.1.1تعريف
5.1.1تعريففرض كنيد yتابعي از xباشد هر معادله اي به
)(n
صورت ) F(x,y,y,…,yرا كه Fدر آن تابعي ازn+2
متغير y ، xو nمشتق اول yنسبت به xباشد يك معادله ي
ديفرانسيل معمولي مرتبه ي nام مي ناميم.
282.
توجه كنيد منظور) y (nاز مشتق nام yنسبت به xاست و مرتبهي يك معادله ي ديفرانسيل برابر با مرتبه ي باالترين مشتق
موجود در معادله است.
283. 5.1.2تعريف
5.1.2تعريفتابع ) y=f(xرا يك جواب معادله ي ديفرانسيل
)(n
F(x,y,y,…,y )=0
در فاصله ي Iمي ناميم.در صورتي كه به ازاي هر xمتعلق
به Iتابع )y=f(xو مشتق هاي آن در معادله صدق كنند.
284.
مجموعه ي تمام جوابهاي معادله را جواب عمومي معادله ميناميم.
منظور از حل يك معادله ي ديفرانسيل به دست آوردن جواب
عمومي آن است.
285. 5.1.4تعريف
5.1.4تعريفمعادله ي ديفرانسيل مرتبه ي ام
با شرايط اوليه
را كه در آن ها اعداد معيني هستند يك مسئله با مقادير اوليه مي ناميم.
286.
توجه كنيد كه براي معادله ي ديفرانسيل مرتبه ي nام nشرطاوليه وجود دارد .اين شرايط مقادير تابع مجهول و )(n-1
مشتق اول آن را در نقطه ي x0معين مي كنند.مي توان
نشان داد كه با وضع محدوديتهايي بر Fيك مسئله با مقادير
اوليه داراي يك مجواب منحصر به فرد است .اين جواب را
جواب خصوصي مسئاله مي ناميم.
287. 5.1.7تعريف
5.1.7تعريفيك معادله ي ديفرانسيل با مشتقات جزيي معادله ايست كه
شانل يك تابع مجهول چند متغيره (بيش از يك متغير) همرام
با مشتقات جزيي آن باشد.
288. 5.2معادلات ديفرانسيل جدايي پذير
5.2معادالت ديفرانسيل جدايي پذير289.
در اين بخش روش حل معادالت ديفرانسيلي را بررسي ميكنيم كه مي توان متغيرهاي آنها را از يكديگر جدا كرد.
290. 5.2.1تعريف
5.2.1تعريفمعادله ي ديفرانسيل مرتبه ي اول p(x)dx+q(y)dy=0را
كه در آن pو qدو تابع حقيقي به ترتيب در فاصله هاي I1
و I2پيوسته اند يك معادله ي ديفرانسيل جدايي پذير مي
ناميم.
291.
با انتگرالگيري مستقيم از اين معادله جواب عمومي آن بهصورت زير به دست مي آيد.
∫p(x)dx+ ∫q(y)dy=c


























































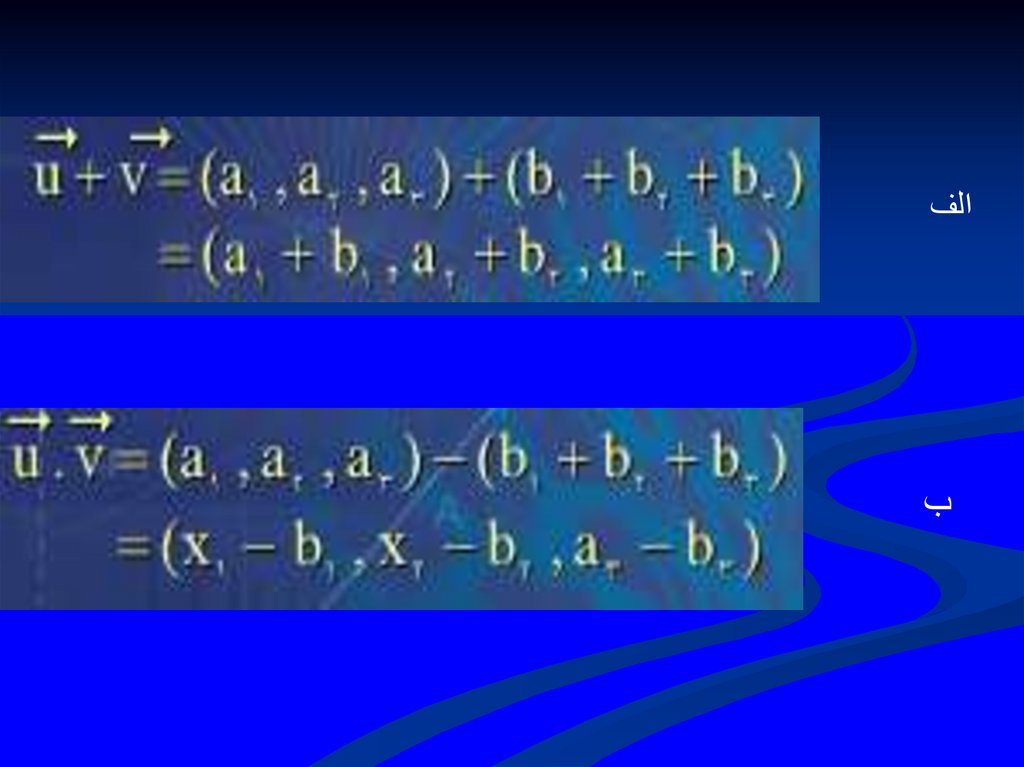

































































































































































































































 Математика
Математика







