Похожие презентации:
Арифметическая и геометрическая прогрессии
1. Урок повторения и обобщения по теме: «Арифметическая и геометрическая прогрессии»
2. Мягкая посадка
• Что вы можете сказать об арифметическойпрогрессии?
• Что вы можете сказать о геометрической
прогрессии?
3. Устная работа
Перед вами последовательности чисел:1) 7; 7; 7;…
2) 1; 4; 9; 16;…
3) 4; – 4; 4; – 4; 4…
4) 0,5; 1; 1,5; 2;…
5) – 2; 8; –12; 28;…
6) 1; 2; 4; 8; 16;…
Под каким номером записана геометрическая прогрессия?
Укажите знаменатель геометрической прогрессии.
4.
1) 7; 7; 7;… , q = 13) 4; – 4; 4; – 4; 4…, q = –1
6) 1; 2; 4; 8; 16;…, q = 2
5.
1) 7; 7; 7;…2) 1; 4; 9; 16;…
3) 4; – 4; 4; – 4; 4…
4) 0,5; 1; 1,5; 2;…
5) – 2; 8; –12; 28;…
6) 1; 2; 4; 8; 16;…
Под каким номером записана арифметическая
прогрессия? Укажите разность арифметической
прогрессии.
6.
1) 7; 7; 7;…,d=0
4) 0,5; 1; 1,5; 2;…, d = 0,5.
7.
Рассмотрим геометрическую прогрессию 1; 2;…Укажите ее девятый член.
Найдите сумму первых 10 ее членов.
8. b9 = 1∙28 = 256
S 101 210 1
1023
2 1
9.
Рассмотрим арифметическую прогрессию 0,5; 1;…Укажите ее шестой член.
Найдите сумму семи первых ее членов.
10. a6=0,5+0,5∙5=3
2 0,5 0,5 6S7
7 14
2
11. Из предложенных формул выберите ту, которая является характеристическим свойством арифметической прогрессии
аn =a1+d (n – 1)Sn
2a1 d (n 1)
n
2
a1 a n
Sn
n
2
a n 1 a n 1
an
2
bn b1 q n 1
b1 (q n 1)
Sn
q 1
Sn
bn q b1
q 1
bn2 bn 1 bn 1
12. Из предложенных формул выберите ту, которая является характеристическим свойством геометрической прогрессии
аn =a1+d (n – 1)Sn
2a1 d (n 1)
n
2
a1 a n
Sn
n
2
an
a n 1 a n 1
2
bn b1 q n 1
b1 (q n 1)
Sn
q 1
Sn
bn q b1
q 1
bn2 bn 1 bn 1



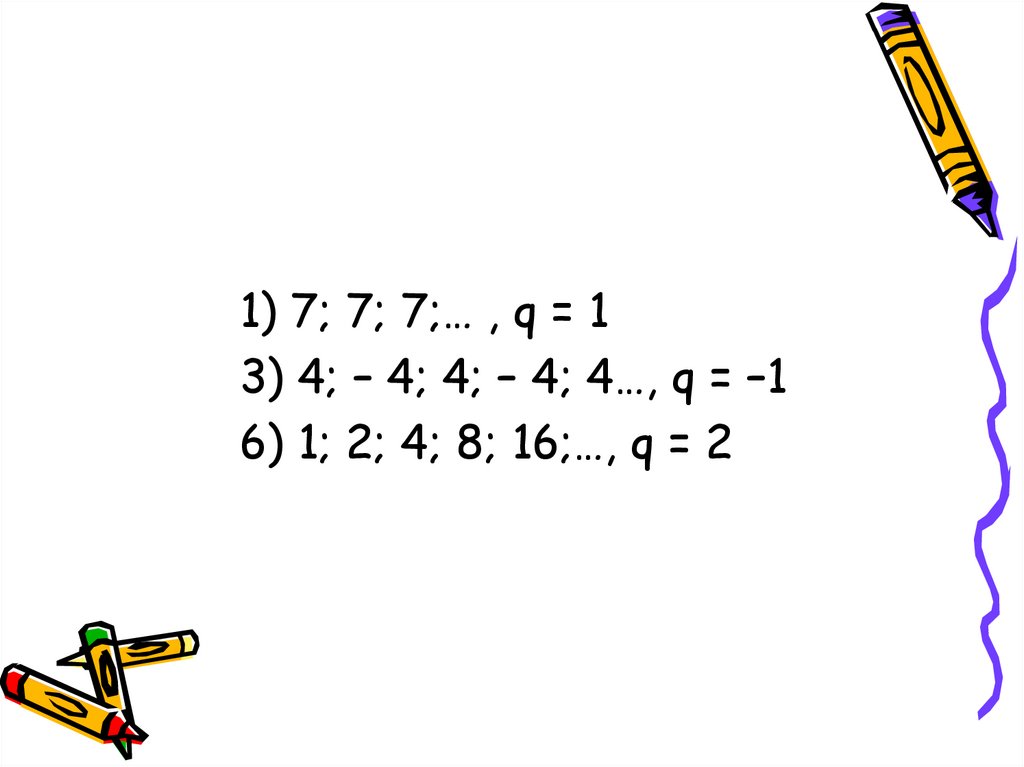



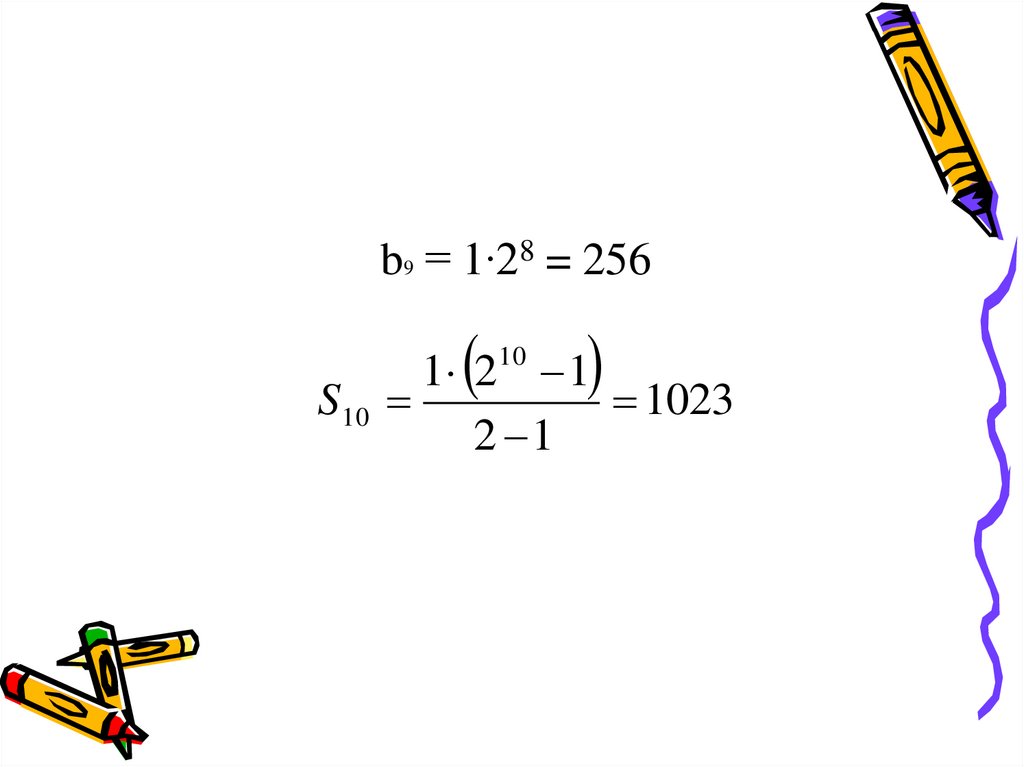




 Математика
Математика








