Похожие презентации:
Использовать на уроке повторения темы «Логарифмы»
1.
Презентацию подготовилаДудоладова М.П.
Учитель математики.
Использовать на уроке
повторения темы
«Логарифмы».
2. a)Log₅(6+X)=2; X=19
Задания первой частиa)Log₅(6+X)=2; X=19
б)Log₆(4+X)=2; X=32
2
в)Log₃(X²+X)=Log₃(X²+3);
X=3
3.
№ 2.2 Log 7 6
2
7 *7
Log 7 6
3 Log 3 12
3 *3
Log 3 12
а )7
б )3
№3.
а)
б)
84
5
Log 5 7
42
2
Log 2 3
3
84
12;
7
42
14
3
294;
324.
4.
5.
№5. Найдите наибольшеезначение функции
У=Ln(х+6)⁹-9х на [-5,5;0]
У=9Ln(х+6)-9х;
D(у): х+6>0
х>-6
D(у)=(-6;+∞)
-6
6.
99
У’=
х 6
D(У’)= (-∞; -6)U(-6;+∞)
9
9;
х 6
х 6 1;
х 5.
7.
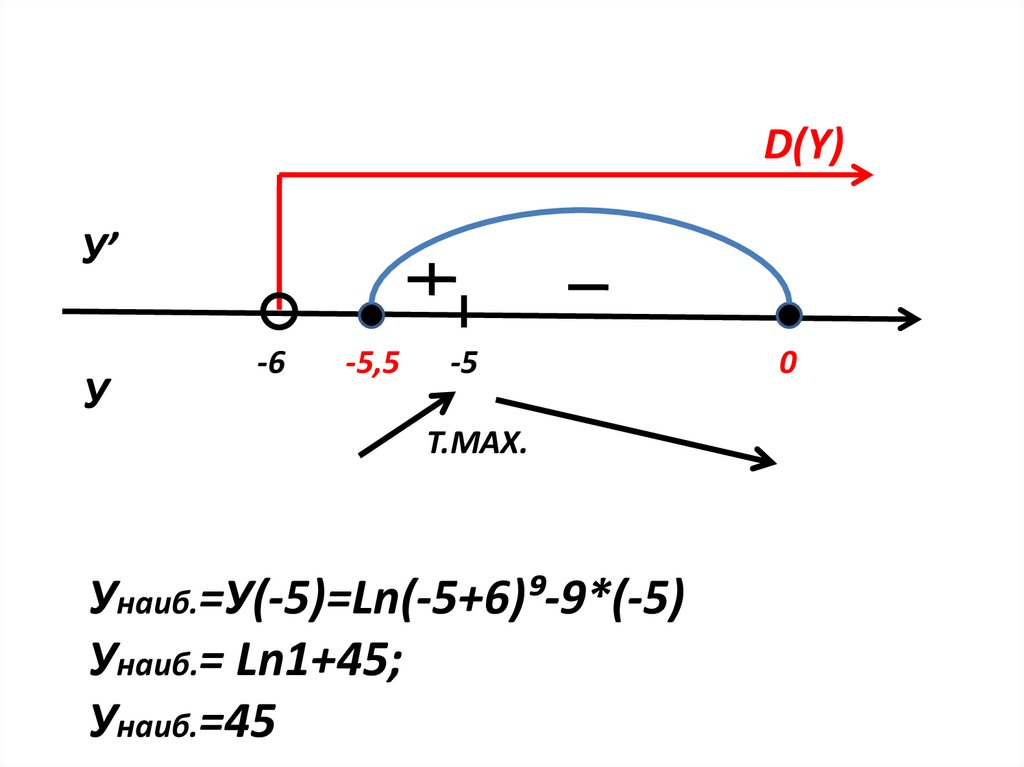
D(Y)У’
У
-6
-5,5
-5
Т.MAX.
Унаиб.=У(-5)=Ln(-5+6)⁹-9*(-5)
Унаиб.= Ln1+45;
Унаиб.=45
0
8. №1.Решить систему неравенств
Задания второй части.№1.Решить систему неравенств
log₄(25-x²)≤2+log₄(x+4) (*)
log₀,₄(2|X+4|+|X-6|-18)<1 (**)
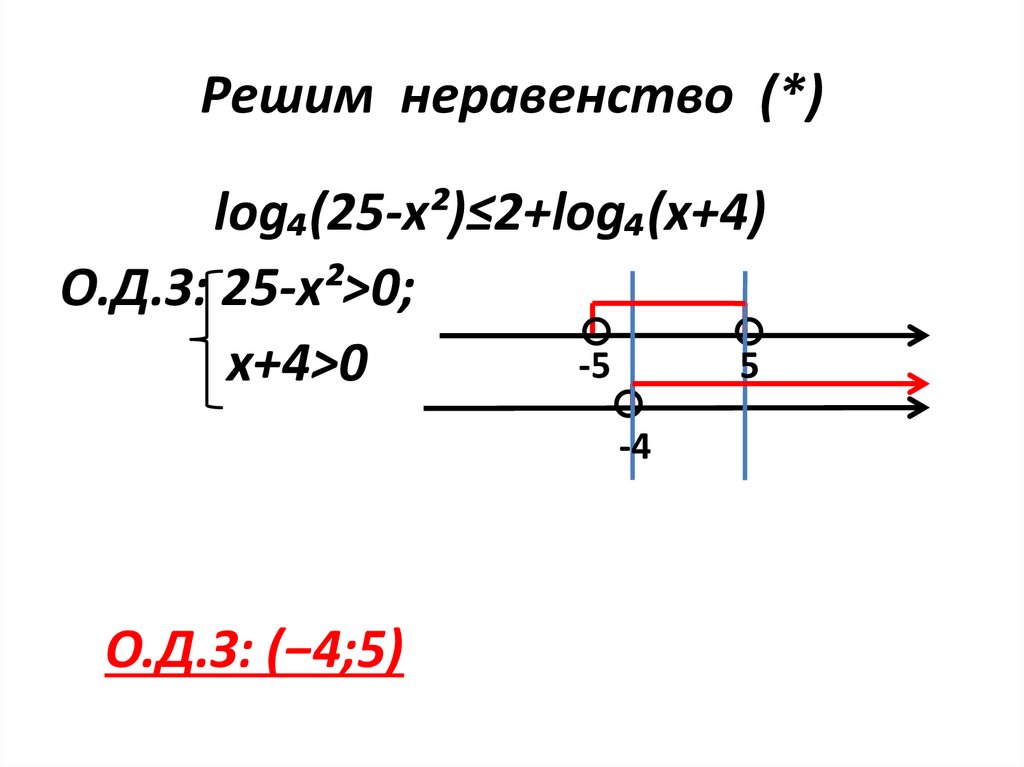
9. Решим неравенство (*)
log₄(25-x²)≤2+log₄(x+4)О.Д.З: 25-x²>0;
-5
5
x+4>0
-4
О.Д.З: (−4;5)
10.
log₄(25-x²) ≤ 2 log₄4+log₄(x+4);log₄(25-x²) ≤ log₄(16x+64);
Функция f(x)= log₄t возрастающая,
т.к. a=4,a>1,то
25-x² ≤ 16x+64;
x² + 16x+64-25≥0;
x² + 16x+39≥0
11.
x² + 16x+39≥0D=256-4*1*39=100>0;
X₁=-3; X₂=-13
-13
(-∞;-13]U[-3;+∞)
-3
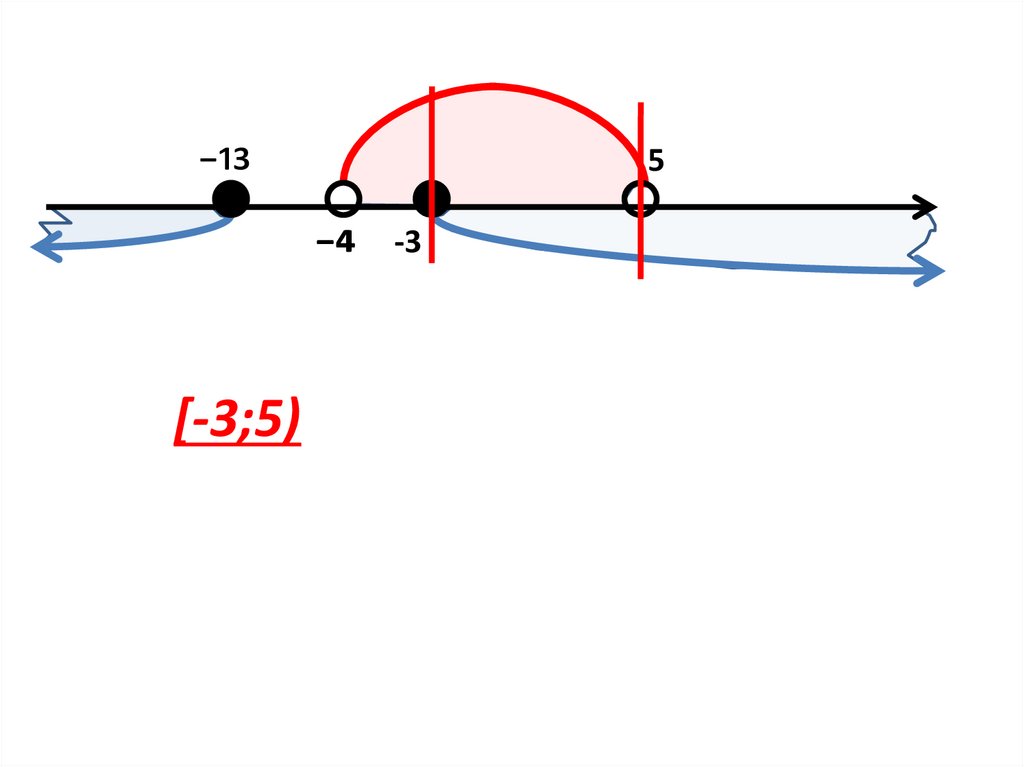
12.
5⁻¹³
⁻⁴
[-3;5)
-3
13.
Решим неравенство (**)log₀,₄(2|X+4|+|X-6|-18)<1
Т.к. -3 ≤ x<5,то
log₀,₄(2 (Х+4)+(6-Х)-18) < log₀,₄0,4;
log₀,₄(Х-4) < log₀,₄0,4;
О.Д.З: Х-4>0;
Х>4
4
14.
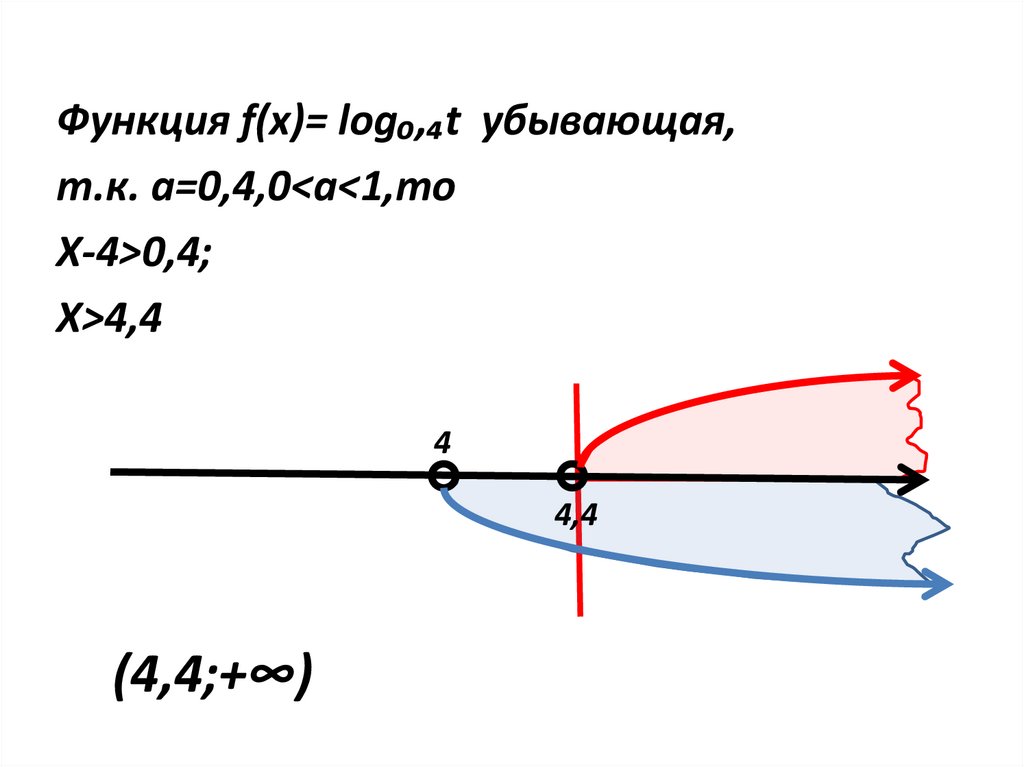
Функция f(x)= log₀,₄t убывающая,т.к. a=0,4,0<a<1,то
Х-4>0,4;
Х>4,4
4
4,4
(4,4;+∞)
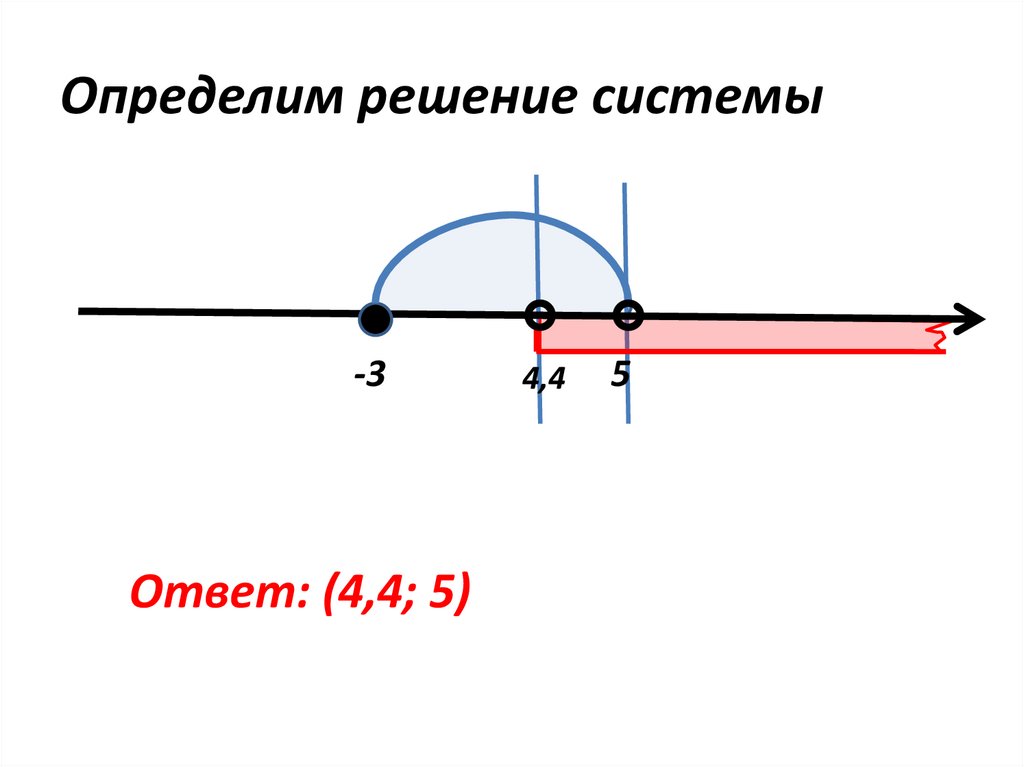
15.
Определим решение системы-3
Ответ: (4,4; 5)
4,4
5
16.
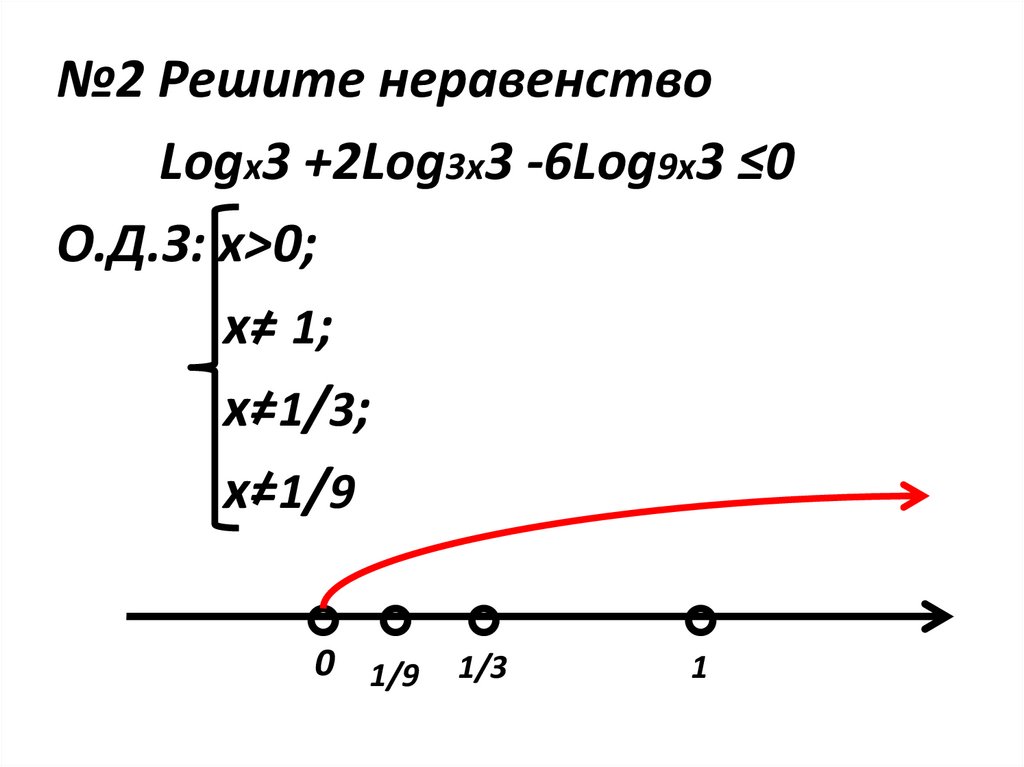
№2 Решите неравенствоLogx3 +2Log3x3 -6Log9x3 ≤0
О.Д.З: х>0;
х= 1;
х=1/3;
х=1/9
0 1/9 1/3
1
17.
12
6
0;
Log 3 x Log 3 3 x log 3 9 x
1
2
6
0.
Log 3 x 1 Log 3 x 2 Log 3 x
Пусть
Log 3 x y, то
1
2
6
0
y 1 y 2 y
18.
2 3у у 4 у 2 у 6 у 6 у0;
у(1 у)(2 у)
2
3у у 2
0.
у(1 у)(2 у)
2
2
2
19.
3у2
у 2 0;
D 1 24 25;
2
у1 1; у 2 ;
3
у (1 у )( 2 у ) 0;
у 0; у 1; у 2
20.
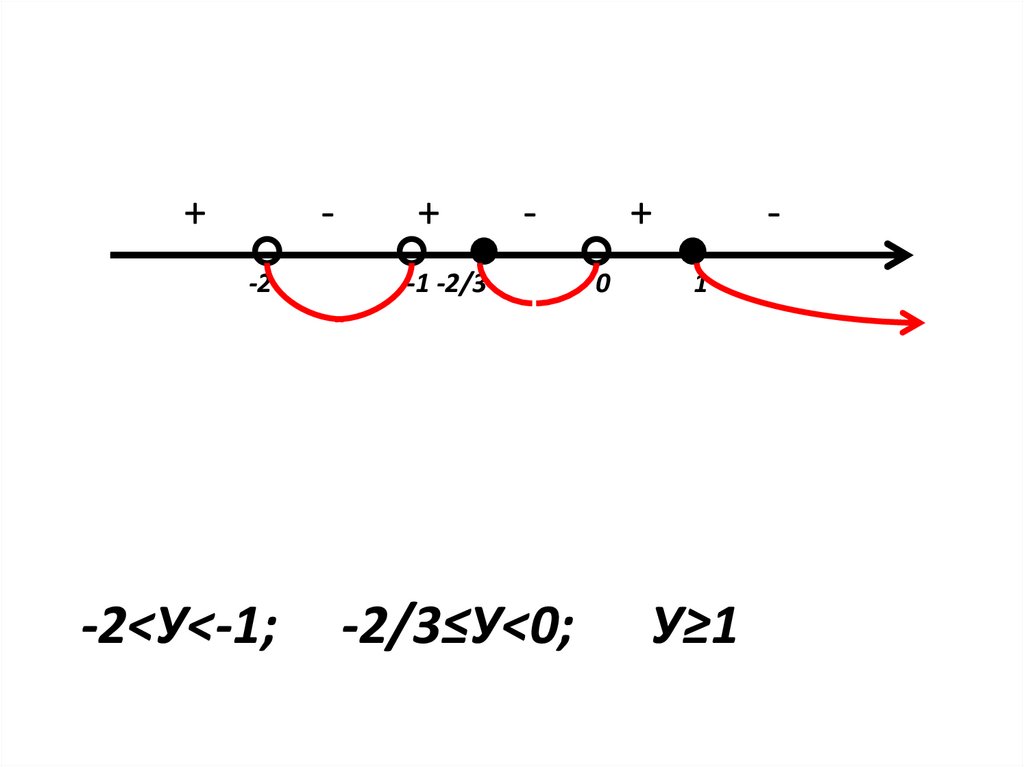
+-2
-2<У<-1;
+
-
-1 -2/3
-2/3≤У<0;
+
0
1
У≥1
21.
2 y 1;1
1
Log 3 Log 3 x Log 3 ;
9
3
1
1
x
9
3
22.
2у 0;
3
Log 3 3
3
2
3
2
3
Log 3 x Log 31;
х 1.
23.
у 1;Log 3 у Log 3 3;
у 3.
0 1/9 1/3
3
2
3
1
1
1
x ;3
9
3
2
3
3
х 1; х 3
24.
№3 При каких значениях хсоответственные значения
функций f=Log 3 x и g= Log3 (3 x)
будут отличаться больше, чем
на 2?
25.
Log 3 x Log 3 (3 x) 2;О.Д.З: Х>0;
3-Х>0
0
3
(0;3)
26.
Log 3 x Log 3 (3 x) Log 3 9;Log 3 x Log 3 (3 x ) Log 3 9;
x 27 9 x;
x 2,7
0
(2,7; 3)
2,7
3
27.
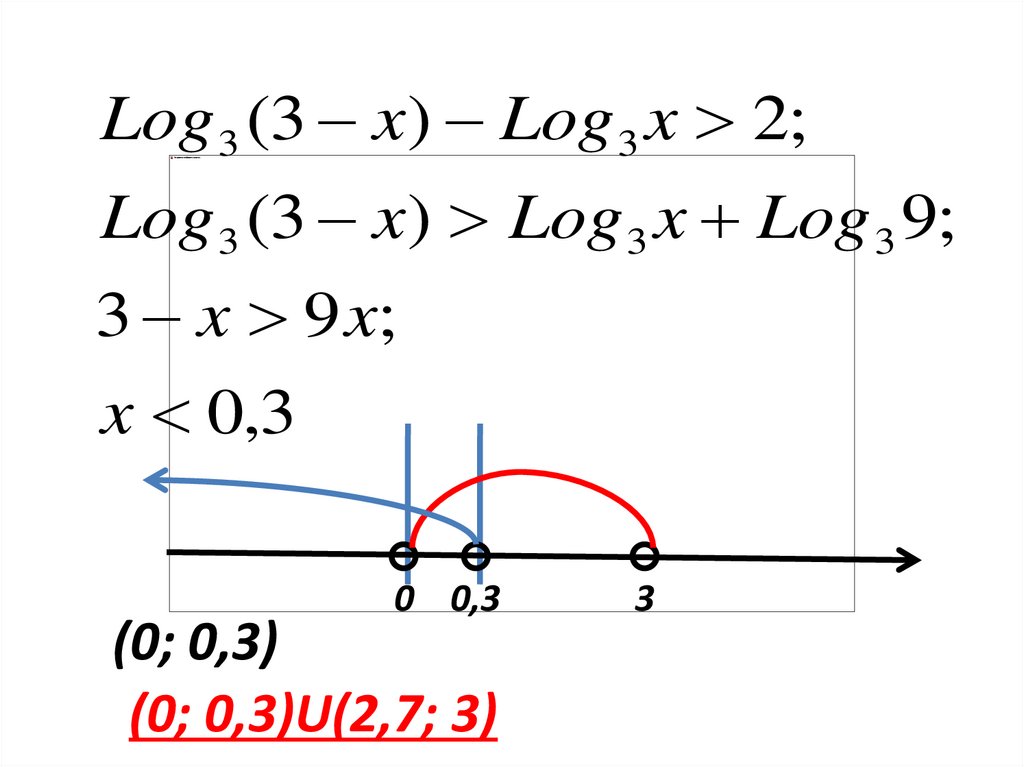
Log 3 (3 x) Log 3 x 2;Log 3 (3 x) Log 3 x Log 3 9;
3 x 9 x;
x 0,3
0 0,3
(0; 0,3)
(0; 0,3)U(2,7; 3)
3


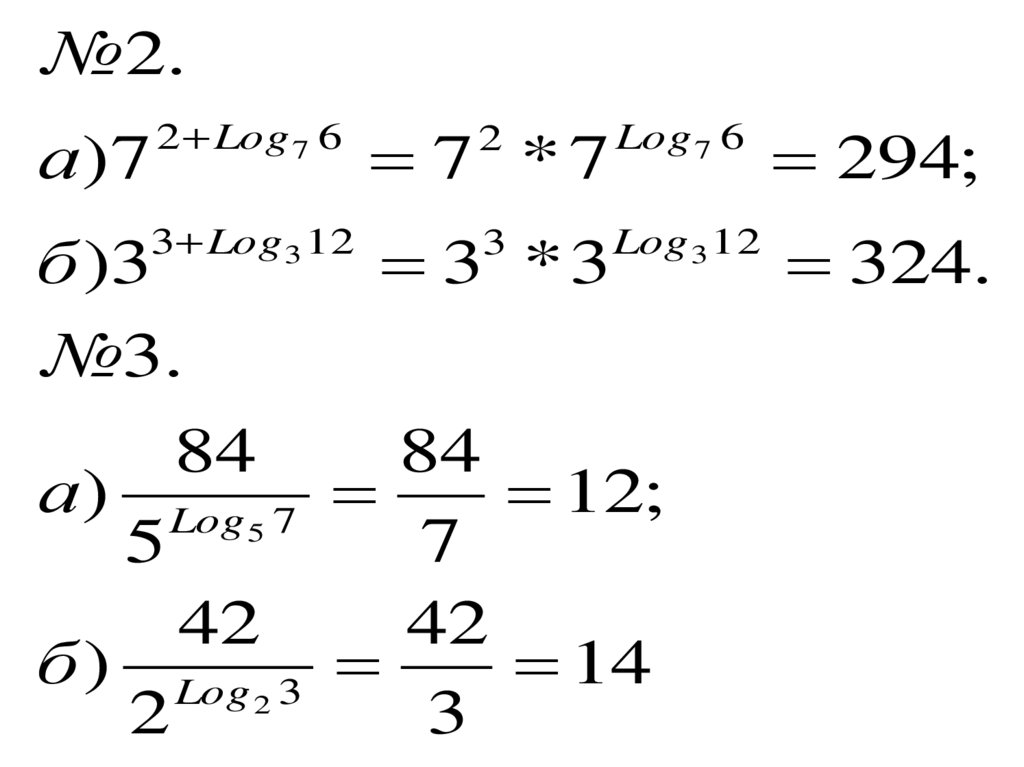
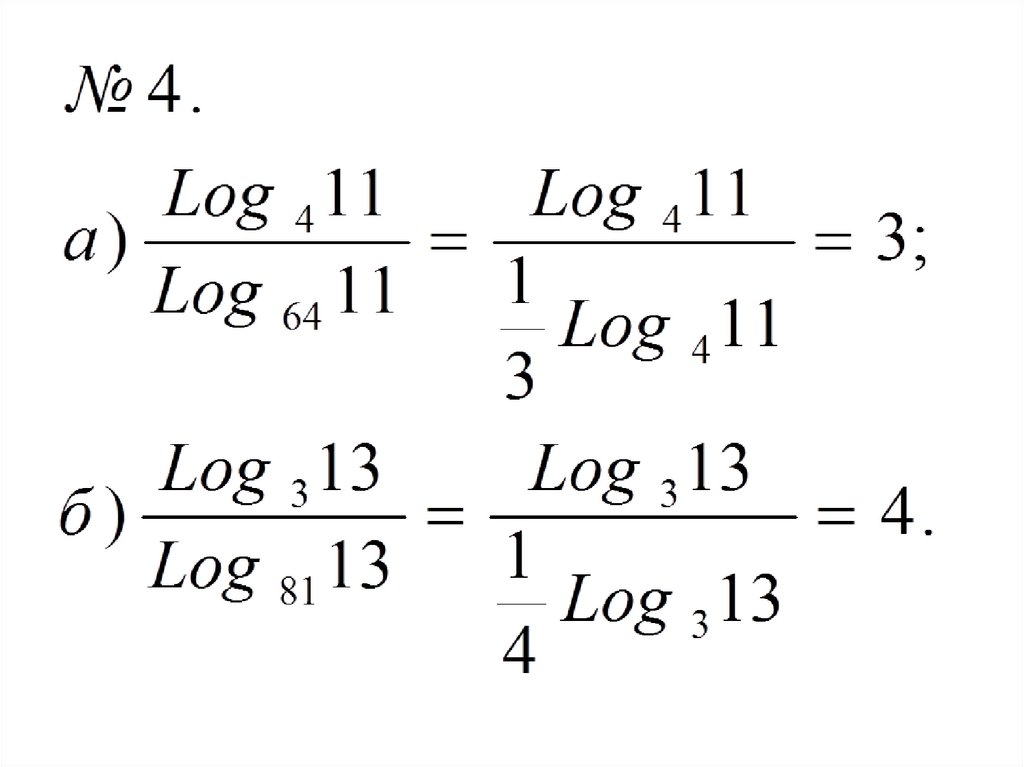

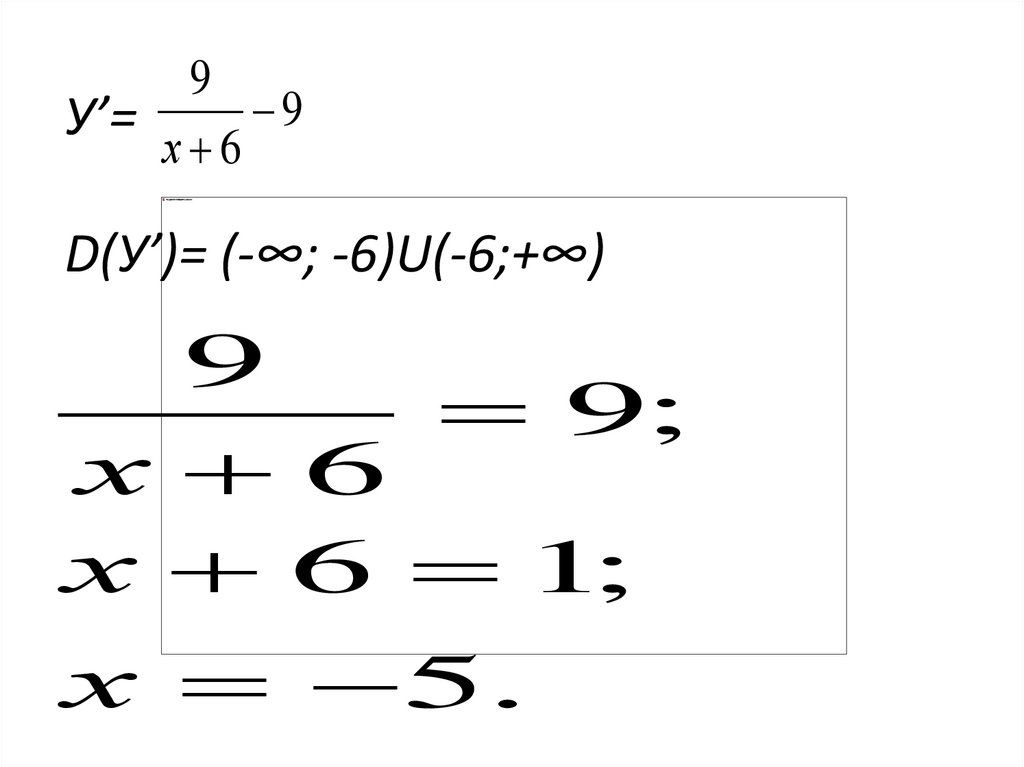


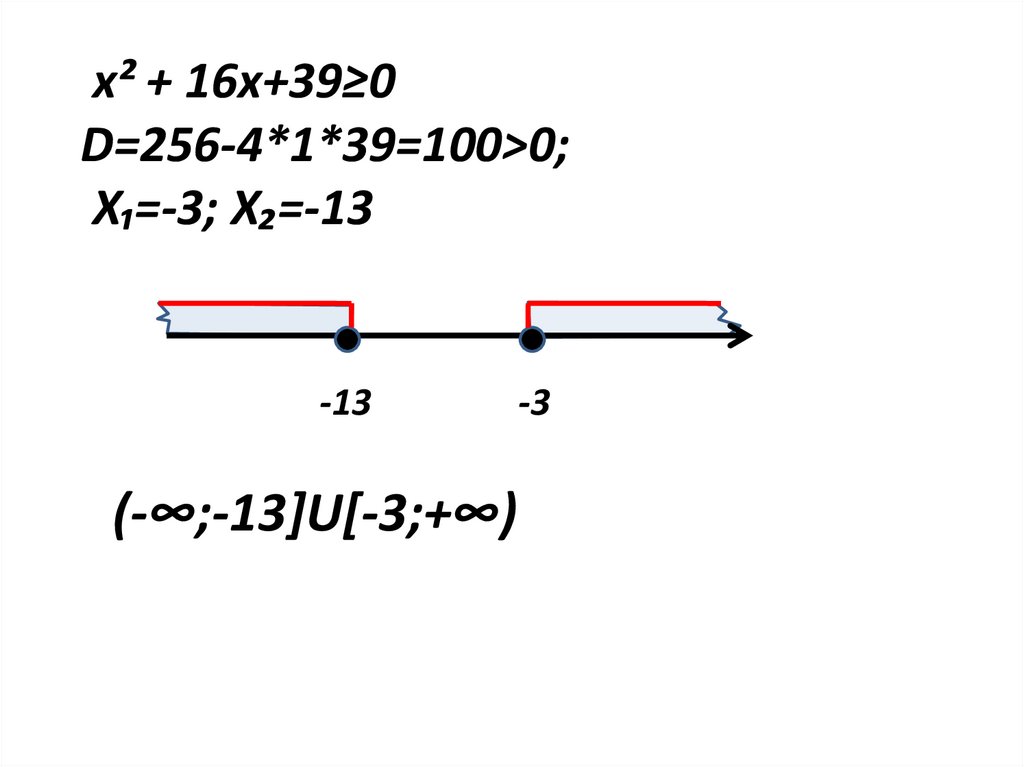

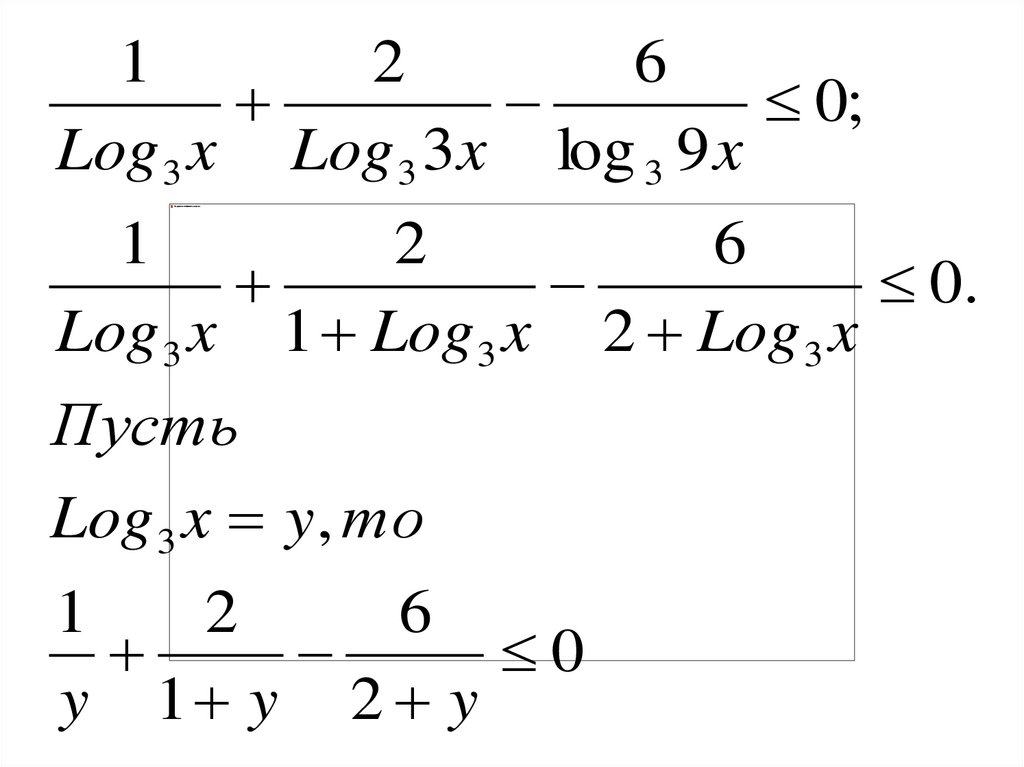

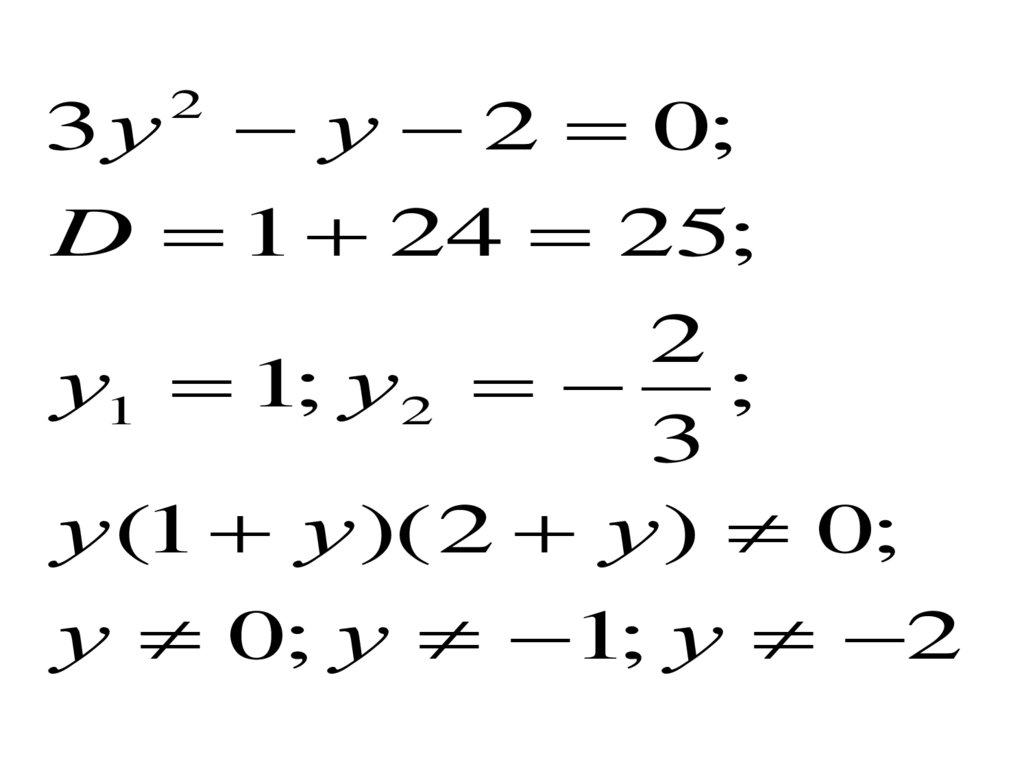
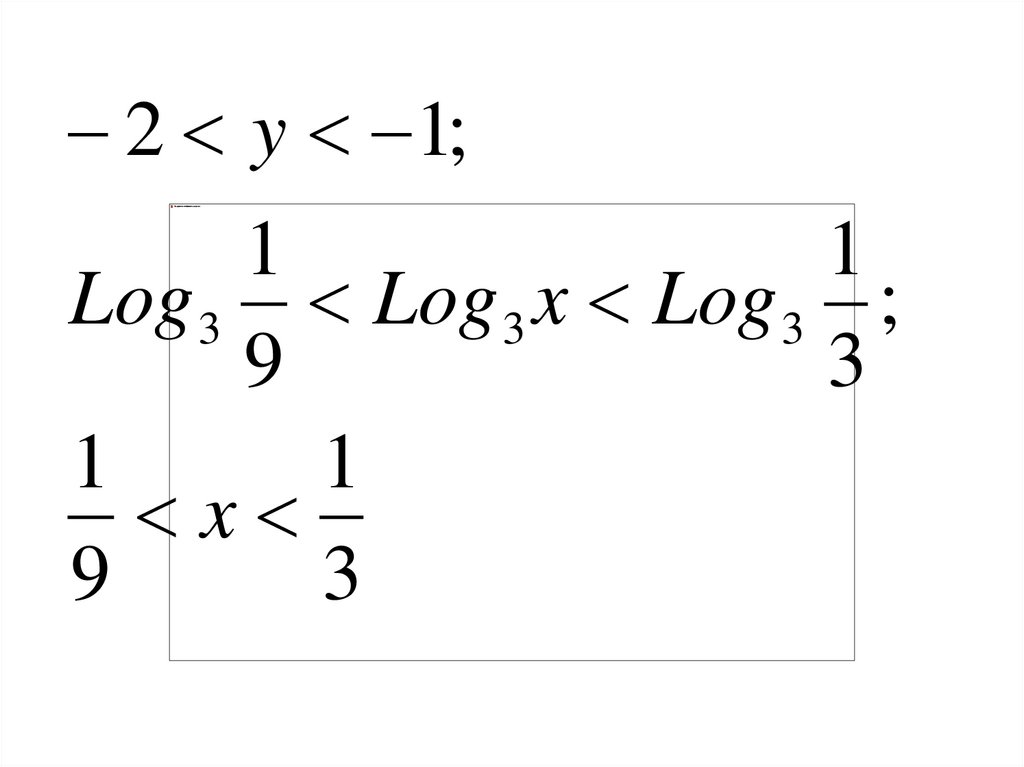
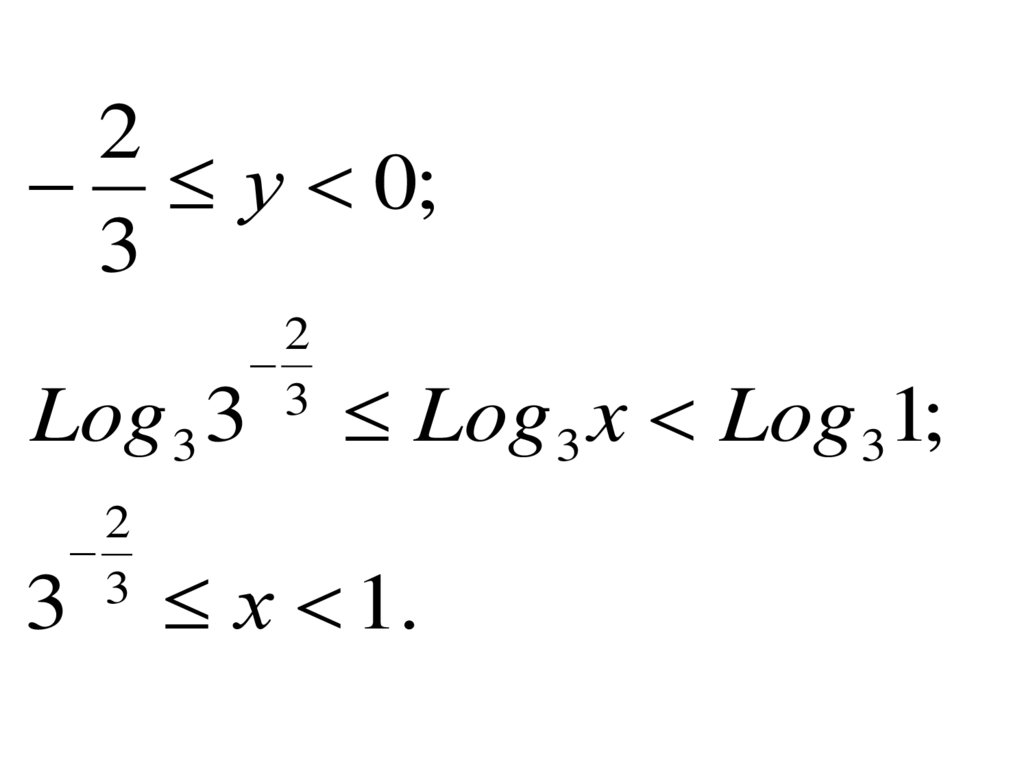
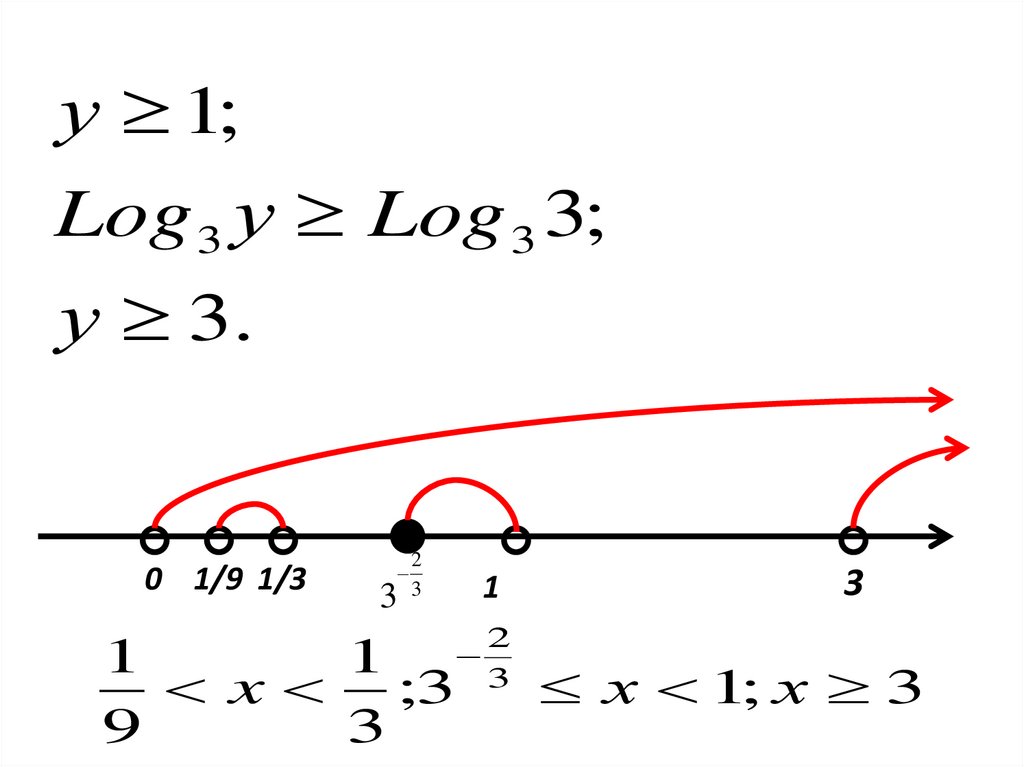

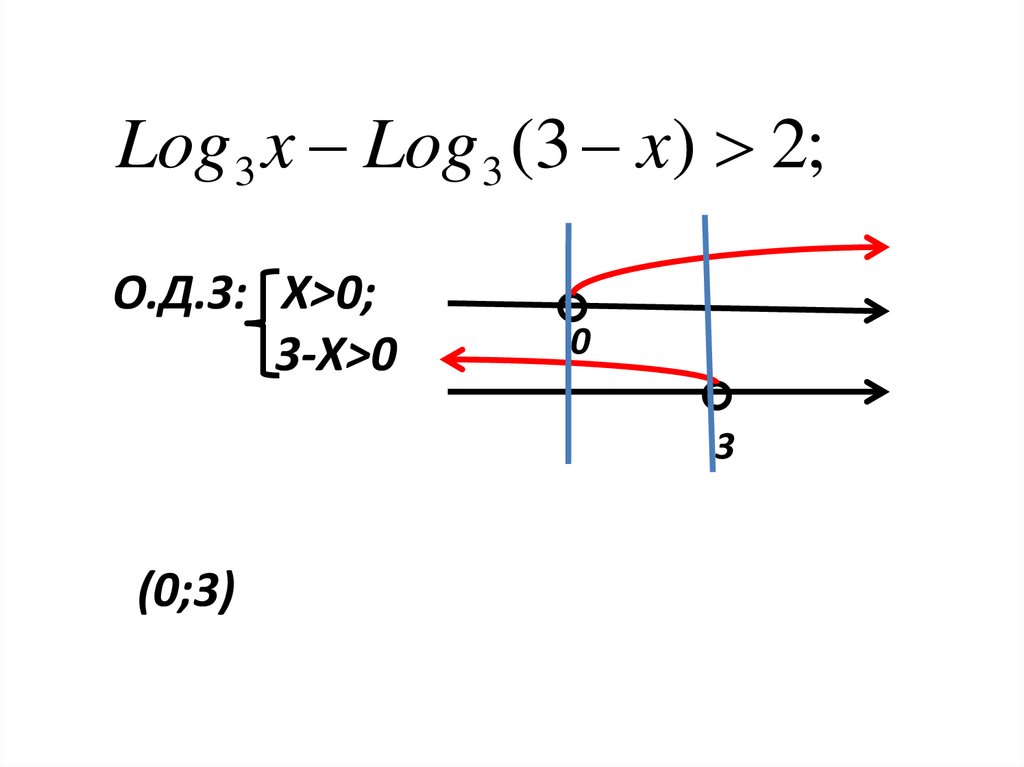
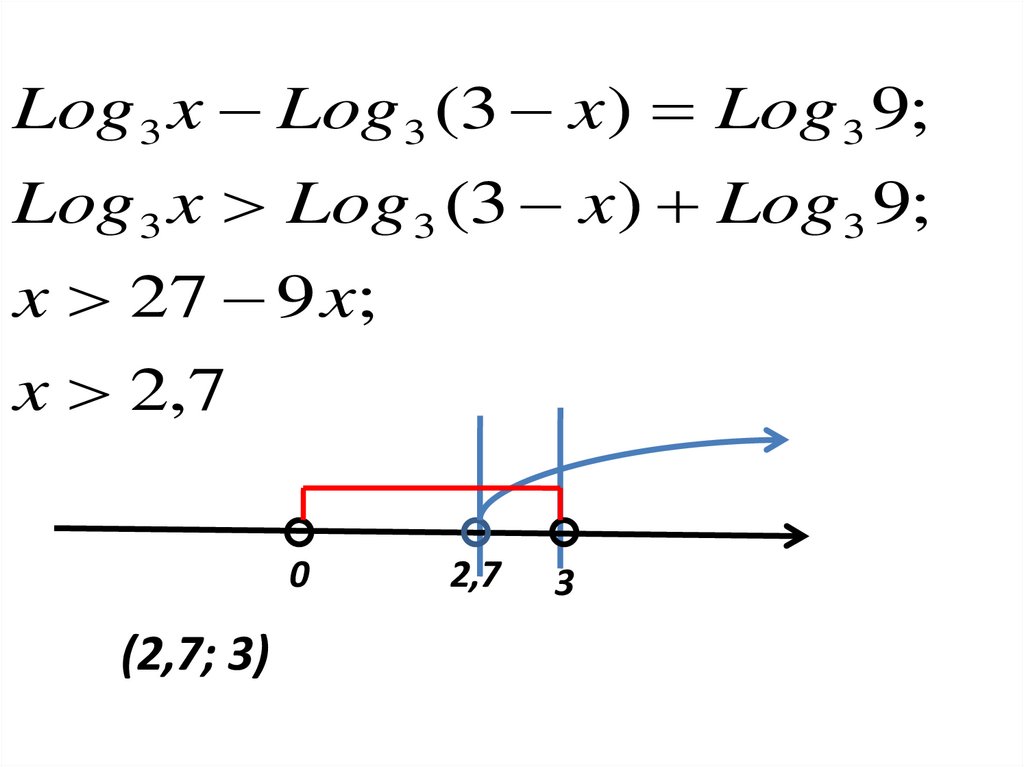
 Математика
Математика








