Подготовка к ЕГЭ. Площади фигур

1.

Информационно-коммуникационное сопровождение
обучения математике
Курсовая работа
учителя математики
Фадеевой Екатерины Павловны.
ПОДГОТОВКА к ЕГЭ -2012.
Площади фигур.
Решение задач В3.
ГБОУ Гимназия № 261
Кировского р-на
Санкт-Петербурга.

2. ЦЕЛИ :

• Повторение темы
«Площади геометрических фигур»
• Создание презентации
для подготовки уч-ся к экзаменам.

3. СОДЕРЖАНИЕ:

1. Разминка.
2. Повторение.
3. Основные типы задач.
4. Формула Пика.
5. Тест.
6. Интерактив .
выход

4. Формула Пика

1.
2.
Задача о площади трапеции.
Формула Пика.
3. Применение формулы для решения задачи 1.
4. Задачи .
содержание

5.

1
Задача 1
Найти площадь фигуры .
C
B
SIV
SII
D
SIII
Первый способ:
Sквадрата = 4·4= 16 ;
SI
SI=(4·2):2=4 ;
A
S ABCD=S квадрата-(SI+SII+SIII+SIV +S кв)
SII= SIV=(1·2):2=1 ; SIII=(1·3):2=1,5 ;
S кв = 1 .
S ABCD=16-(4+1+1,5+1 +1)= 7,5
Формула Пика
содержание

6.

Формула
Пика :
Если дан многоугольник на некоторой клетчатой решетке, вершины
которого находятся в узлах этой клетчатой решетки , то тогда его
площадь можно найти по следующей формуле:
S многоугольника = В + Г : 2 - 1
В - кол-во точек пересечения линий решетки внутри фигуры
Г - кол-во точек на границе фигуры.
задача
содержание

7.

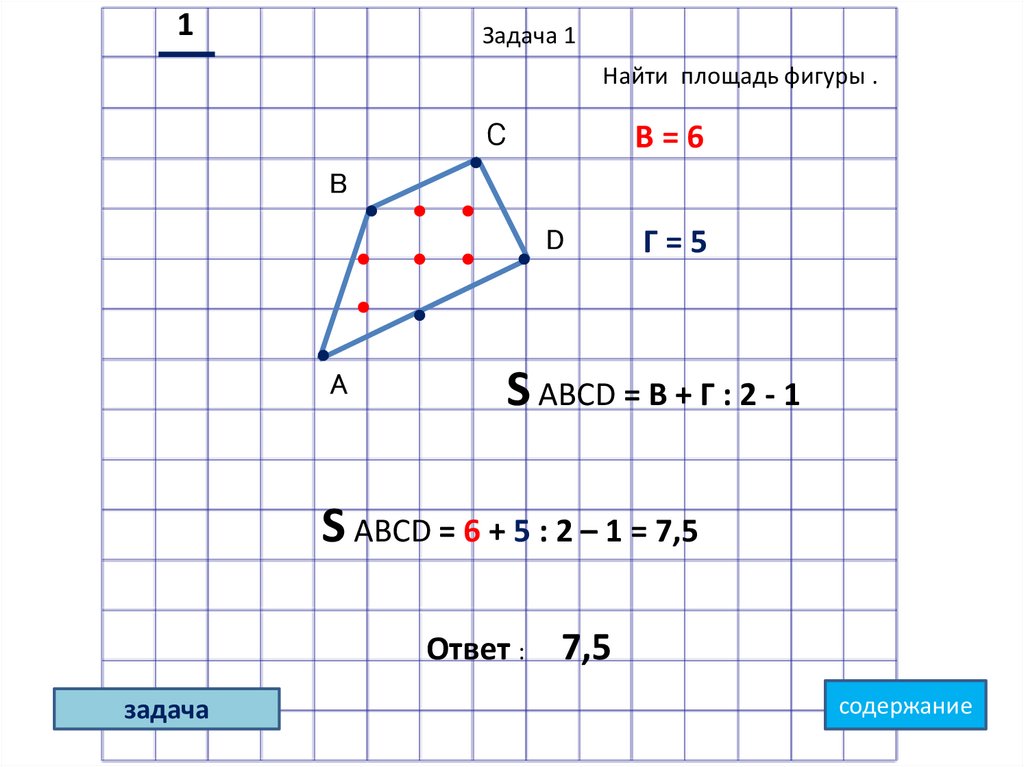
1
Задача 1
Найти площадь фигуры .
С
В=6
B
D
A
Г=5
S ABCD = В + Г : 2 - 1
S ABCD = 6 + 5 : 2 – 1 = 7,5
Ответ :
задача
7,5
содержание

8.

Заполните пропуски в тексте :
1.Если
х1;у1 и
имеет координаты………..
b х2;у2
a
- данные векторы , то вектор a b
a х;у
2
2
a
x
y
вычисляется по формуле……..
3.Если А(х1;у1) и В(х2;у2)-данные точки, то AB
…
4. Расстояние d между точкой М
выражается формулой …
х1-х2;у1-у2
2. Длина вектора
x2 x1 2 y2 y1 2
( х ; у ) и началом координат
d x2 y2
5.Если даны две точки М1(х1;у1) и М2(х2;у2) ,то расстояниеd между ними
выражается формулой ...
d
x2 x1 2 y2 y1 2
содержание

9. Основные формулы:

многоугольник
Формула площади
Треугольник
произвольный
a h
S
2
а- основание
треугольника,
h-высота .
Прямоугольный
треугольник
a b
S
2
а; в –катеты
прямоугольного
треугольника
Прямоугольник
Трапеция
Круг
а; в –смежные стороны
прямоугольника
S ab
а; в –основания трапеции;
h-высота .
a b
S
h
2
S R
2
R – радиус круга.
содержание

10.

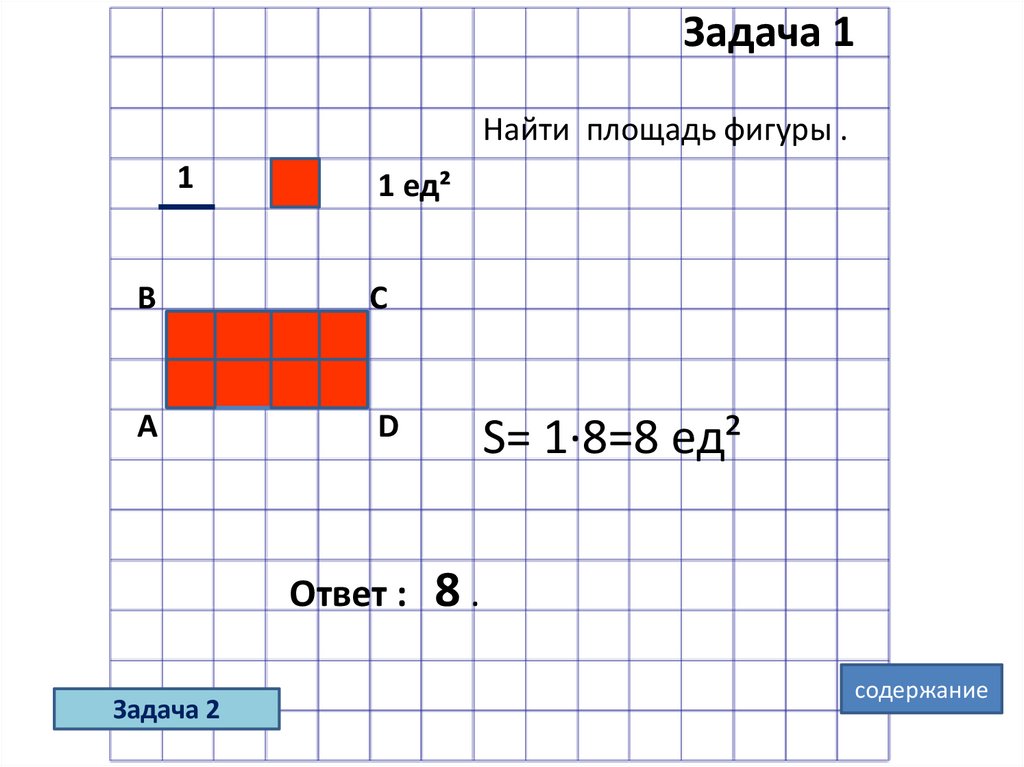
Задача 1
Найти площадь фигуры .
1
1 ед²
B
С
А
D
Ответ :
Задача 2
S= 1·8=8 ед²
8.
содержание

11.

Задача 2
Найти площадь фигуры .
1
1 ед²
B
С
А
a=1
b=5
h=4
S =(1 +5) :2 ·4=12
D
Ответ : 12.
содержание
Задача 2 (продолжение)

12.

Задача 2
Найти площадь фигуры .
1
1 ед²
B
С
А
S = 1·10 + 4·S Δ
S Δ =1:2
S = 1·10 + 4·(1:2)=12
D
Ответ : 12.
Задача 3
содержание

13.

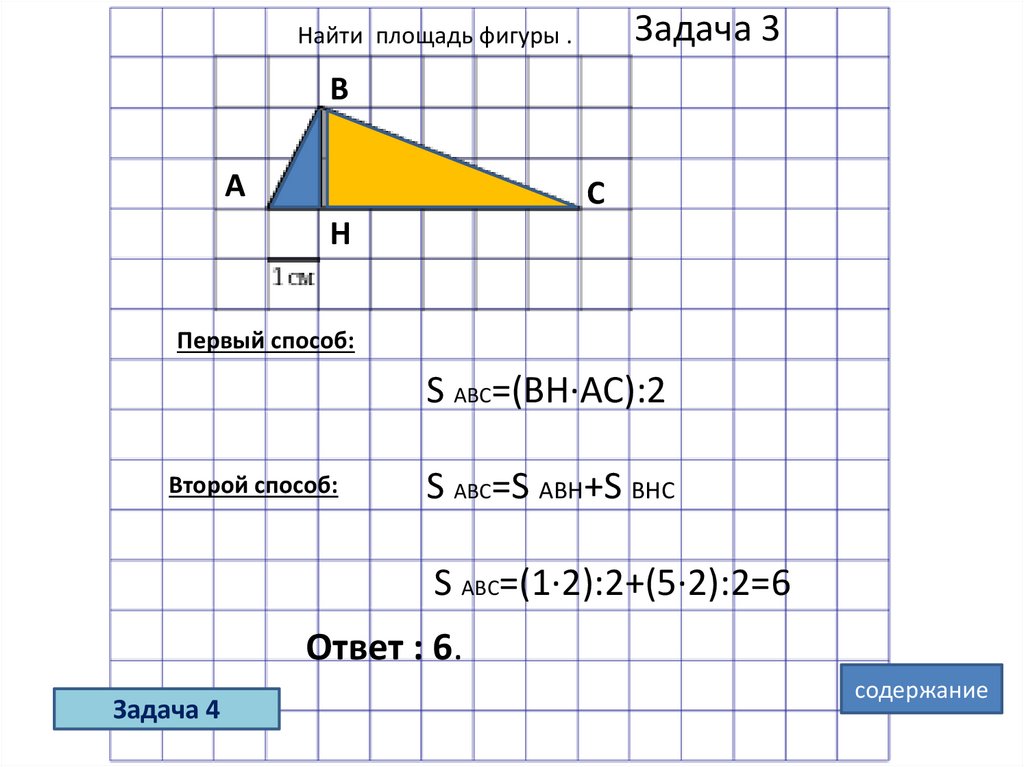
Задача 3
Найти площадь фигуры .
B
A
C
H
Первый способ:
S ABC=(BH·AC):2
Второй способ:
S ABC=S ABH+S BHC
S ABC=(1·2):2+(5·2):2=6
Ответ : 6.
Задача 4
содержание

14.

Задача 4
Найти площадь фигуры .
а
h
а= 3 ;
h= 8 ;
S= ·a· h = 12 · 3 · 8 = 12
1
2
Ответ : 12.
Задача 5
содержание

15.

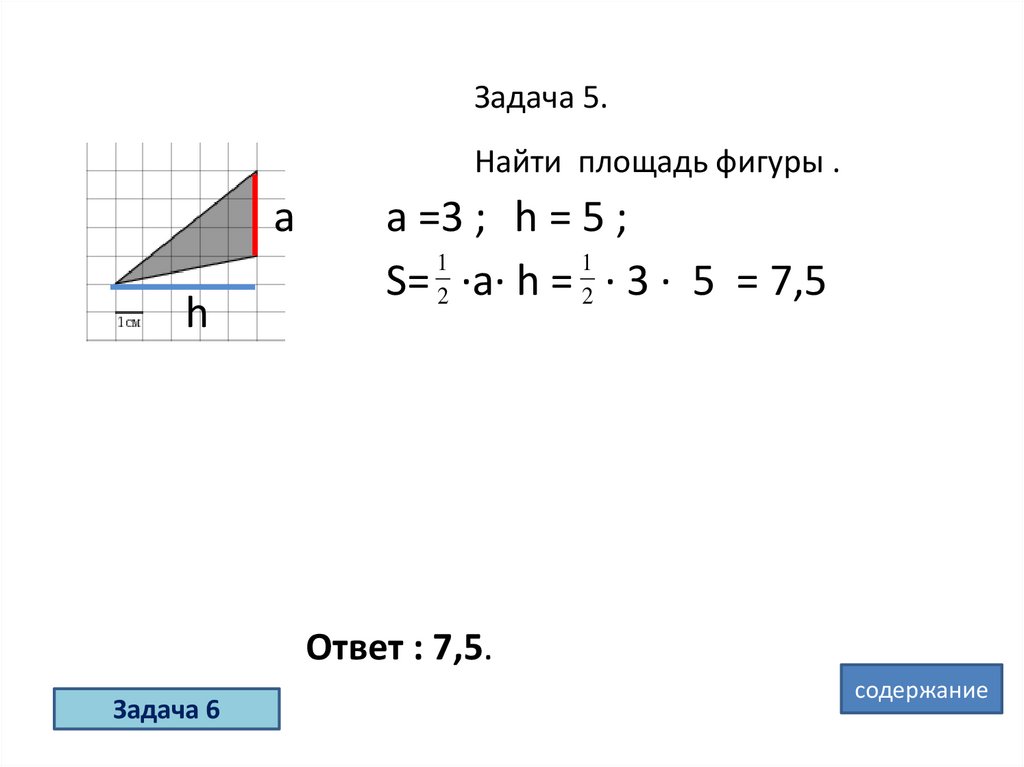
Задача 5.
Найти площадь фигуры .
а
h
а =3 ; h = 5 ;
1
1
S= 2 ·a· h = 2 · 3 · 5 = 7,5
Ответ : 7,5.
Задача 6
содержание

16.

Задача 6
Найти площадь фигуры .
а
а=2; h=3;
h
h
S= 2·S= 2·
1
·a· h = 2 · 3
2
=6
Ответ : 6.
Задача 7
содержание

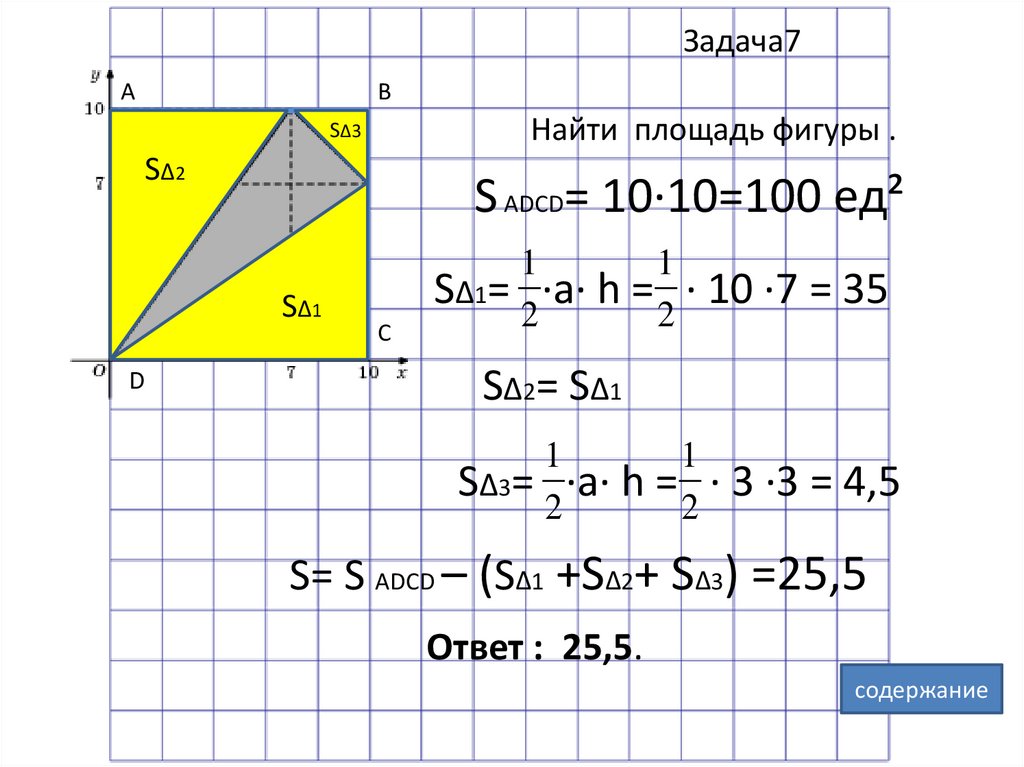
17.

Задача7
A
B
Найти площадь фигуры .
SΔ3
SΔ 2
S ADCD= 10·10=100 ед²
SΔ 1
D
C
1
1
SΔ1= ·a· h = · 10 ·7 = 35
2
2
SΔ2= SΔ1
1
1
SΔ3= ·a· h = · 3 ·3 = 4,5
2
2
S= S ADCD – (SΔ1 +SΔ2+ SΔ3) =25,5
Ответ : 25,5.
содержание

18.

Задача 1
Найти площадь фигуры .
В = 10 ;
Г=7
S =В+Г:2-1
S = 10 + 7 : 2 – 1 = 12,5
Ответ :
Задача 2
12,5
содержание

19.

Задача 2
Найти площадь фигуры .
Первый способ:
S = 12 + 8 : 2 – 1 = 15
Второй способ:
S = (1 + 4) : 2 ·6 = 15
Ответ :
15
Формула Пика

20.

ИНТЕРАКТИВ :
www.reshuege.ru
www.mathege.ru
www.interurok.ru
содержание

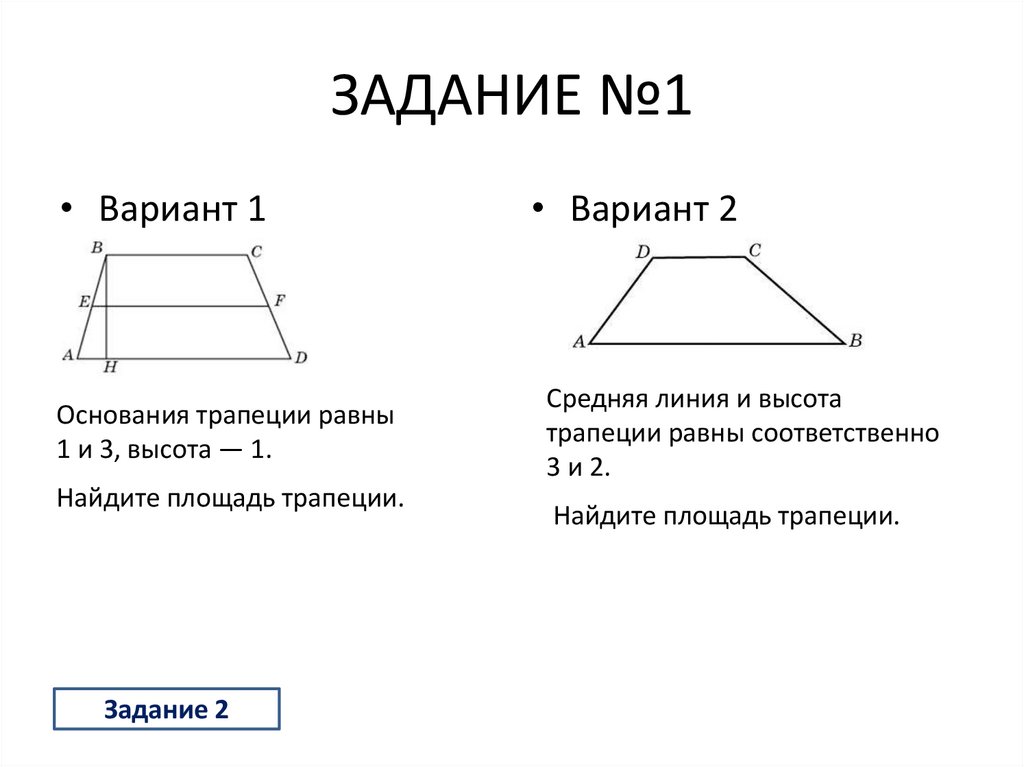
21. ЗАДАНИЕ №1

• Вариант 1
Основания трапеции равны
1 и 3, высота — 1.
Найдите площадь трапеции.
Задание 2
• Вариант 2
Средняя линия и высота
трапеции равны соответственно
3 и 2.
Найдите площадь трапеции.

22. ЗАДАНИЕ №2

• Вариант 1
• Вариант 2
Найдите площадь квадрата,
вершины которого имеют
координаты
На клетчатой бумаге с клетками
размером 1 см х1 см изображен
треугольник (см. рисунок).
(4;3), (10;3), (10;9), (4;9).
Найдите его площадь в квадратных
сантиметрах.
Задание 3

23. ЗАДАНИЕ №3

• Вариант 1
Найдите площадь в
квадратных
сантиметрах.
Задание 4
• Вариант 2
Найдите площадь
прямоугольника ABCD,
считая стороны квадратных
клеток равными 1.

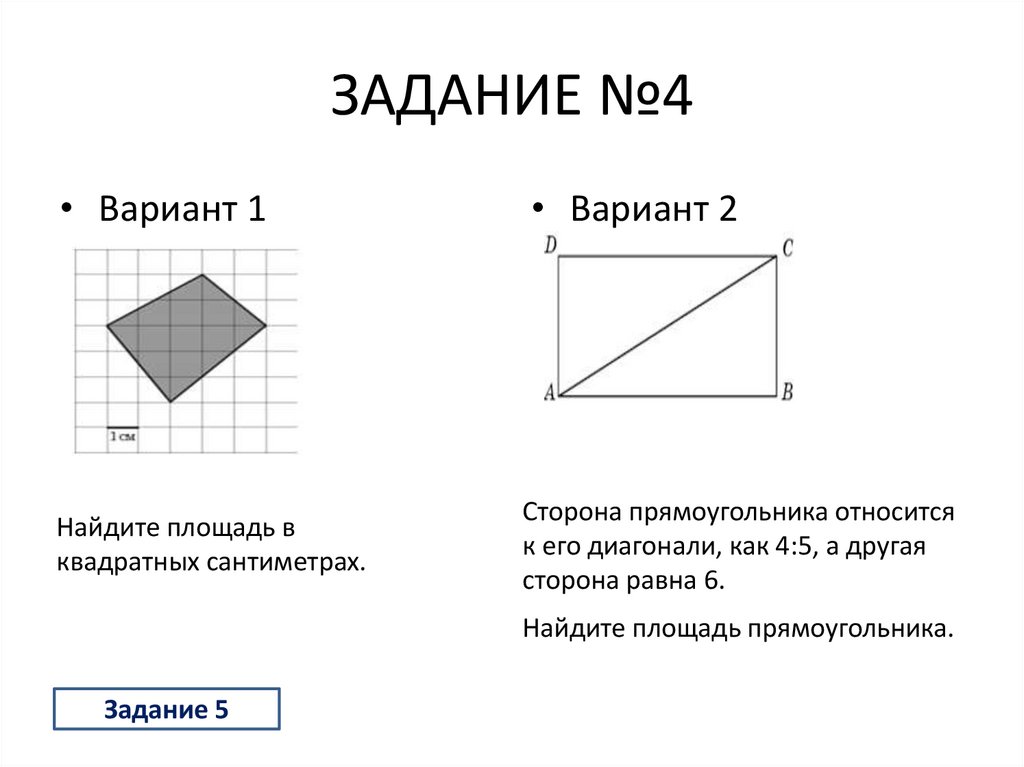
24. ЗАДАНИЕ №4

• Вариант 1
• Вариант 2
Найдите площадь в
квадратных сантиметрах.
Сторона прямоугольника относится
к его диагонали, как 4:5, а другая
сторона равна 6.
Найдите площадь прямоугольника.
Задание 5

25. ЗАДАНИЕ №5

• Вариант 1
• Вариант 2
Площадь прямоугольного
треугольника равна 16.
Один из его катетов равен 4.
Найдите другой катет.
содержание
Найдите площадь треугольника,
вершины которого имеют координаты
(0;0), (10;7), (7;10).
ответы

26. ОТВЕТЫ к ТЕСТУ

1 вариант
1
2
2
36
содержание
3
4
7,5 12,5
2 вариант
5
1
2
3
4
5
8
6
10,5
10
48
25,5