Похожие презентации:
Площадь трапеции. Свойство площадей равных фигур
1.
2. Свойство площадей равных фигур
Равныемногоугольники
имеют равные
площади
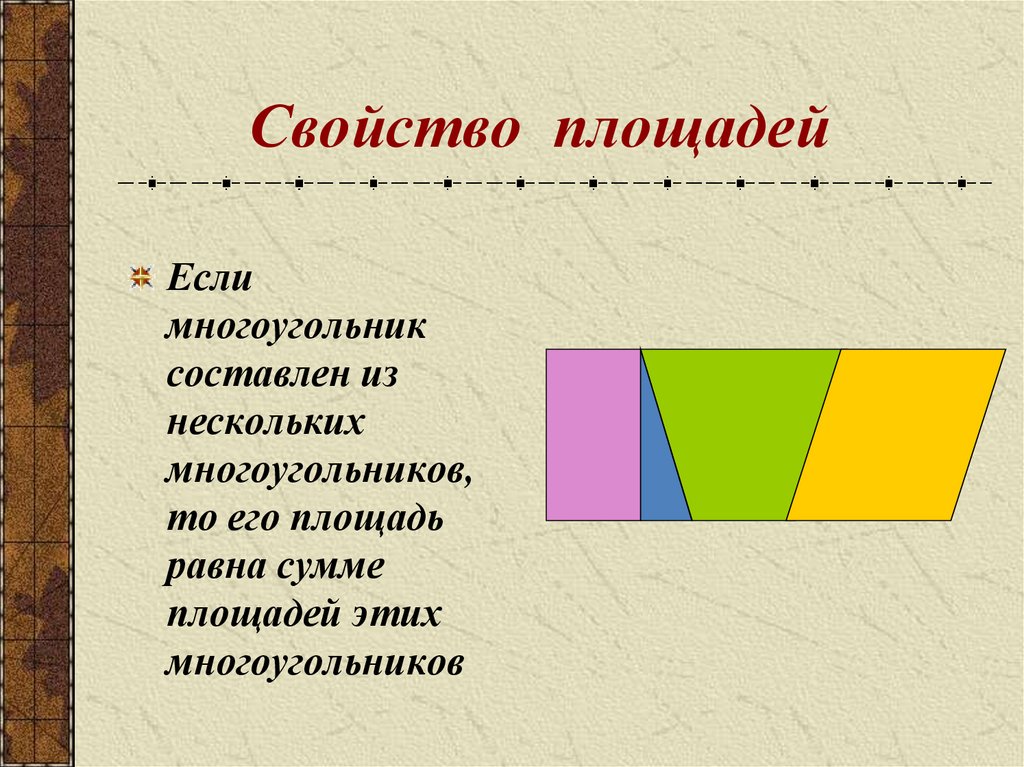
3. Свойство площадей
Еслимногоугольник
составлен из
нескольких
многоугольников,
то его площадь
равна сумме
площадей этих
многоугольников
4. Формулы площадей
аКвадрат
Прямоугольник
Параллелограмм
Треугольник
S = a2
S=a·b
b
a
S=a·h
h
a
S=½a·h
h
a
5.
Еще 4-5 тыс.лет назад вавилонянеумели определять площадь трапеции
в квадратных единицах.
Древние египтяне 4000 лет назад
пользовались почти теми же
приемами, что и мы: сумма
параллельных сторон делилась
пополам и умножалась на высоту.
28.11.2022
5
6.
Определение площадей геометрическихфигур - одна из древнейших
практических задач.
Правильный подход к их решению
был найден не сразу.
Один из самых простых и доступных
способов вычисления площадей был
открыт Евклидом.
При вычислении площадей он
использовал простой прием,
называемый методом разбиения.
28.11.2022
6
7.
Вычисление площадей на РусиПотребность измерения площадей привела к
созданию на Руси рукописей геометрического
содержания чисто практического характера в
XVI веке.
В рукописи «Книга сошного письма» собраны
правила измерения площадей. Трапеция:
площадь трапеции выражается произведением
полусуммы оснований на «хобот», т.е. на
боковую сторону, что тоже неверно.
Вопреки сохранившимся рукописям создание
«русскими мастерами каменных дел»
различных сооружений кремлевских стен и
башен, храмов говорит о том, что эти мастера
28.11.2022
7
8.
• Что называется трапецией?• Что такое основания трапеции?
• Как называют две другие стороны?
• Какие виды трапеций знаете?
9. «Трапеция» - слово греческое, означающее в древности «столик». Отсюда идет название трапеза, трапезная. В «Началах» Евклида
(III в.до н.э.)трапеция – любой четырехугольник (не
параллелограмм). Трапеция в нашем
смысле встречается впервые у
древнегреческого математика Пасидона.
Только в XVIII веке это слово
приобретает современный смысл.
10.
B8см
C
H
6см
30º
Решение:
A
K
D
трапеция ABCD состоит из 2 Δ: ΔABD и ΔBCD
Чтобы найти её площадь надо найти площади этих треугольников.
Проведём высоту BK в ΔABD
и DH в ΔBCD;
SABD =½ AD BK
SABCD = SABD + SBCD
SBCD = ½ BC DH
SABCD = ½ AD BK + ½ BC DH
= ½ BK (AD+BC)
SABCD= ½ BK (AD+BC)
BK- высота, AD,BC- основания
Теорема: Площадь трапеции равна произведению полусуммы её оснований на
высоту
11. Решить задачу
Дано:ABCD-трапецияB
AD=12 см; BC=8см,
6см
AB=6 см, A=30°
A 30º
Найти: S ABCD
К
Решение:
a b
S
2
BC AD
S ABCD
BK
2
8 12
2
S ABCD
3 30( см )
2
h
8см
C
D
12.
• Дайте определение высоты трапеции:а) Назовите высоту у прямоугольной
трапеции.
б) Сколько высот можно построить для
трапеции?
Что о них можно сказать?
13.
Высота трапецииперпендикуляр,проведённый из любой
точки одного из оснований
к прямой, содержащей
другое основание
A
BH- высота
CH1,DH2,MN-высоты трапеции
B
M
C
H2
D
H
N
H1
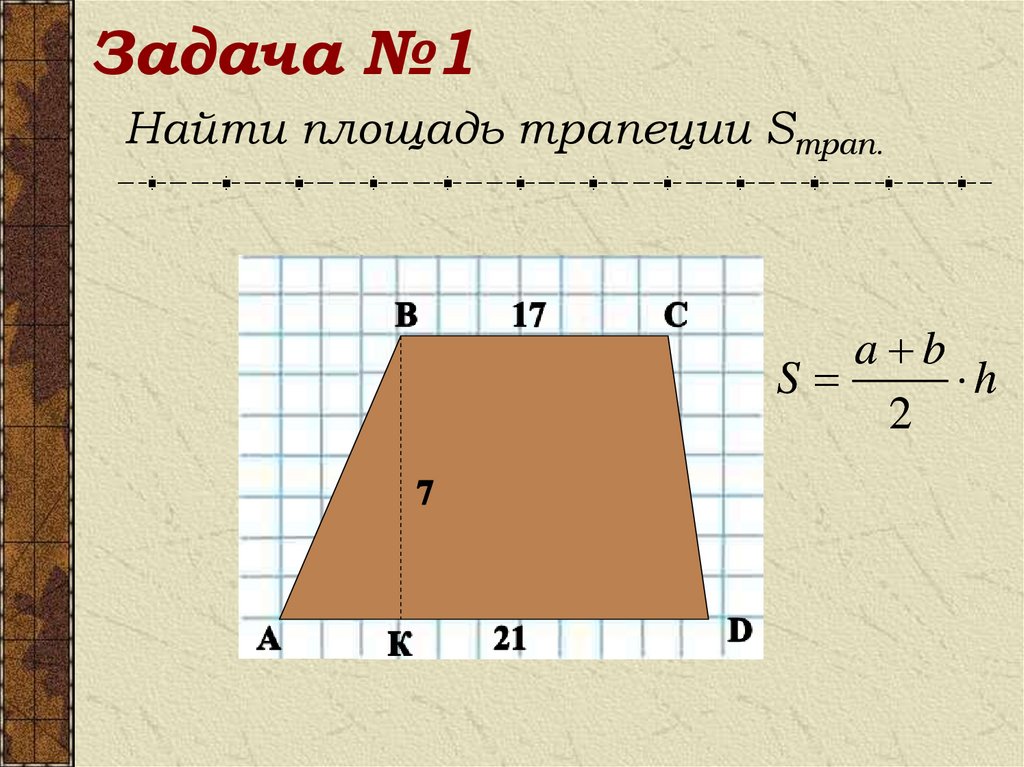
14. Задача №1
Найти площадь трапеции Sтрап.a b
S
h
2
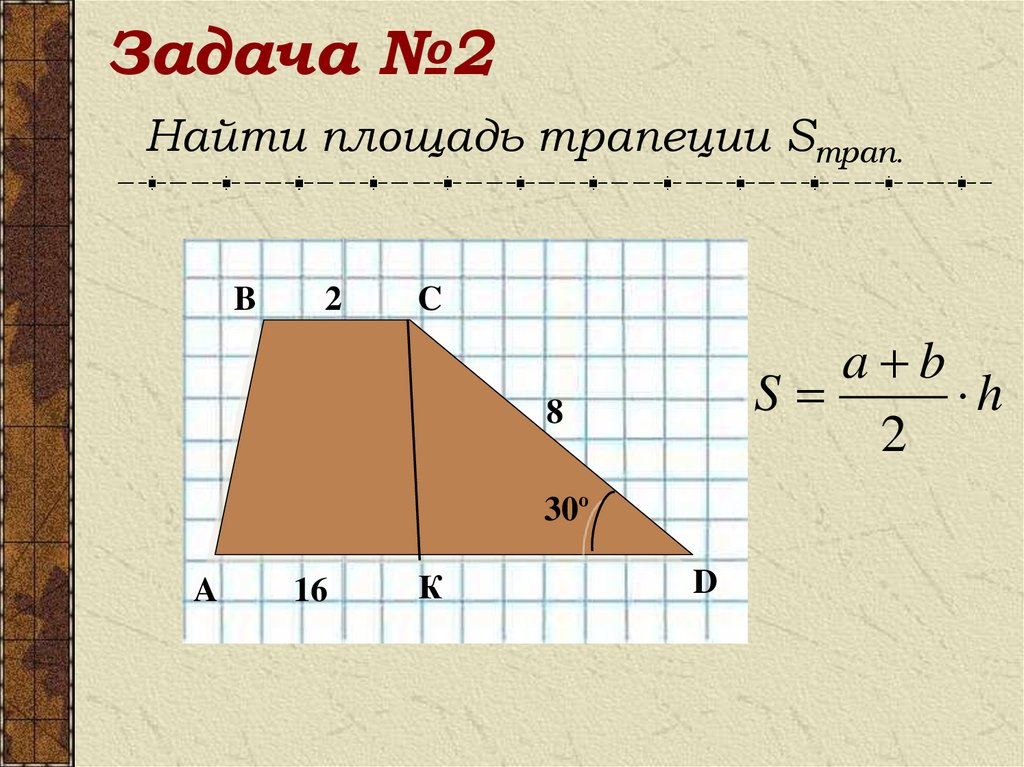
15. Задача №2
Найти площадь трапеции Sтрап.B
2
C
a b
S
h
2
8
30º
A
16
К
D
16. Задача №3
Найти площадь трапеции Sтрап.B
C
К
12
A
Е
ED=18
D
17. Подведем итог:
1. На уроке вывели формулу трапеции.Она имеет вид:
1
S трап = 2 ( AD BC ) BH
2. Научились применять эту формулу для
решения задач.
18. Желаю успеха!
«К большомутерпению
придет
и уменье.»















 Математика
Математика








