Похожие презентации:
Энергия магнитного поля. Объемная плотность энергии
1.
§ 28 Энергия магнитного поля.Объемная плотность энергии.
Глава 3
Электричество и магнетизм
2.
При размыкании цепи, за счет ЭДСсамоиндукции совершается работа, в результате
которой уменьшается энергия катушки
dI
dA S Idt L Idt LIdI
dt
3.
Интегрируя по току, получаемсовершаемую при исчезновении тока
0
2
0
LI
A LIdI
2
I0
работу,
4.
Следовательно, энергия магнитного поля катушки2
0
LI
W
2
5.
Энергия контура сосредоточена в магнитном поле.Возьмем в качестве примера магнитное поле
соленоида. Индуктивность и магнитная индукция
соленоида:
L 0 n V
2
B 0 nI
6.
Выражение для энергии магнитного поля соленоида:2
2
n
V
LI
B
B
0
W
V
2
2
0 n 2 0
2
2
7.
Энергия магнитного поля распределена с некоторойобъемной плотностью в объёме катушки
2
W
B
V 2 0
8.
Энергия поля может быть определена с помощьюинтегрирования по объему
W dV
V
или
W
V
B
2
2 0
dV
9.
Сравнивая два соотношения для магнитного поля,W
V
B
2
2 0
LI
W
2
dV
2
получаем формулу для вычисления индуктивности
контура:
2
L 2
I
2
2
B
V
dV
0
10.
Вычислим энергию магнитного поля двух контуров стоком
W W1 W2 W
1-е слагаемое – энергия 1-го контура
2-е слагаемое – энергия 2-го контура
3-е слагаемое – при возникновении тока во 2-м
контуре в первом контуре возникает ЭДС индукции,
работу которой нужно вычесть.
11.
W A1 i1I1dtdI 2
I1 L12
dt I1L12 I 2
dt
12.
Энергию магнитного поля двух контуров с током2
1 1
2
2 2
LI
LI
W
L12 I 1 I 2
2
2
L11 I1 I 2 L22 I 2 I 2 L12 I 1 I 2 L21 I 2 I 1
W
2
2
2
2
13.
Энергия N-контуров с токами определяется суммой1
W
2
N
i 1
N
k 1
Lik I i I k










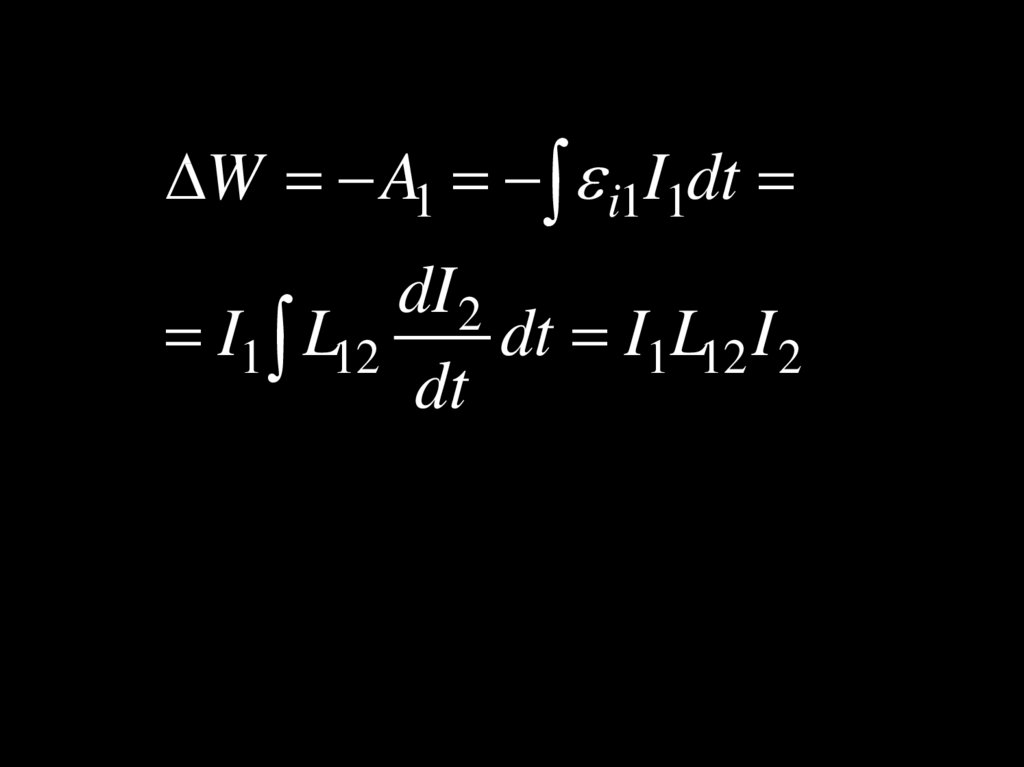


 Физика
Физика








