Похожие презентации:
Разделы физики
1. Физика:
• изучает законы* движения материи;• служит фундаментом для изучения всех специальных дисциплин;
• формирует научное мировоззрение.
_____________
*Законы – устойчивые повторяющиеся объективные
закономерности, существующие в природе
2. Научный подход
1. Постановка проблемы.2. Формулирование одной или нескольких гипотез.
3. Предсказание естественных следствий из каждой гипотезы.
4. Проведение опытов, которые бы подтвердили или опровергли
предсказанные ранее следствия.
5. Формулировка простейшего заключения, в котором
согласовывались бы гипотеза, логические следствия и
эксперимент.
3. Разделы физики
• Механика - раздел физики, наука, изучающая движение материальных тел ивзаимодействие между ними; при этом движением в механике называют
изменение во времени взаимного положения тел или их частей в пространстве.
Кинематикой называют раздел механики, в котором движение тел рассматривается
без выяснения причин, его вызывающих. Динамика - раздел механики, изучающий
законы движения тел в зависимости от действующих на них сил.
• Молекулярно-кинетическая теория - это раздел физики, изучающий свойства тел в
зависимости от характера движения и взаимодействия атомов и молекул этих тел.
Атомы и молекулы рассматриваются в молекулярной физике как наименьшие
частицы химического вещества.
• Термодинамика - это раздел физики изучающий условия и количественные
соотношения взаимопревращений теплоты, работы и других видов энергии без
обращения к молекулярному строению тел.
• Электричество и магнетизм – раздел физики, электрические и магнитные явления.
• Оптика – раздел физики, изучающий природу света, его свойства, законы,
связанные с его распространением.
• Атомная физика — это раздел физики, который изучает строение атомов и
элементарные процессы на атомном уровне.
4. Кинематика
Кинематикой называют раздел механики, в котором движение телрассматривается без выяснения причин, его вызывающих.
Материальная точка – тело, размерами которого в данных
условиях можно пренебречь.
5.
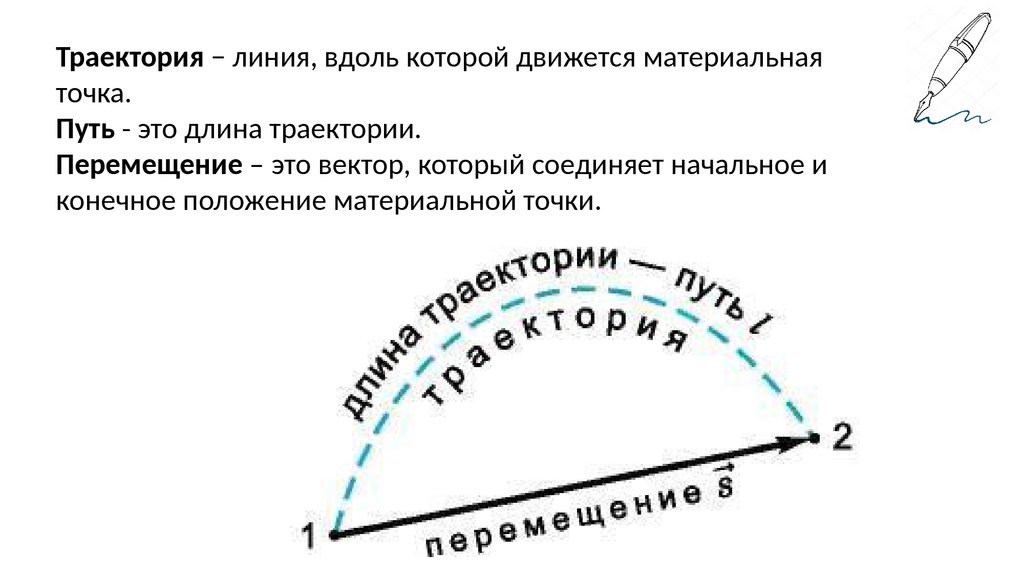
Траектория − линия, вдоль которой движется материальнаяточка.
Путь - это длина траектории.
Перемещение – это вектор, который соединяет начальное и
конечное положение материальной точки.
6.
•Средняя скорость – это физическаявеличина,
равная
отношению вектора перемещения точки к промежутку
времени , за который произошло это перемещение.
– средняя скорость;
- перемещение тела;
– время за которое произошло перемещение.
7.
•Мгновенная скорость – векторная физическая величина, равнаяотношению
перемещения
к
интервалу
времени,
за
который это перемещение произошло, если интервал времени
стремится к нулю.
8. Задача
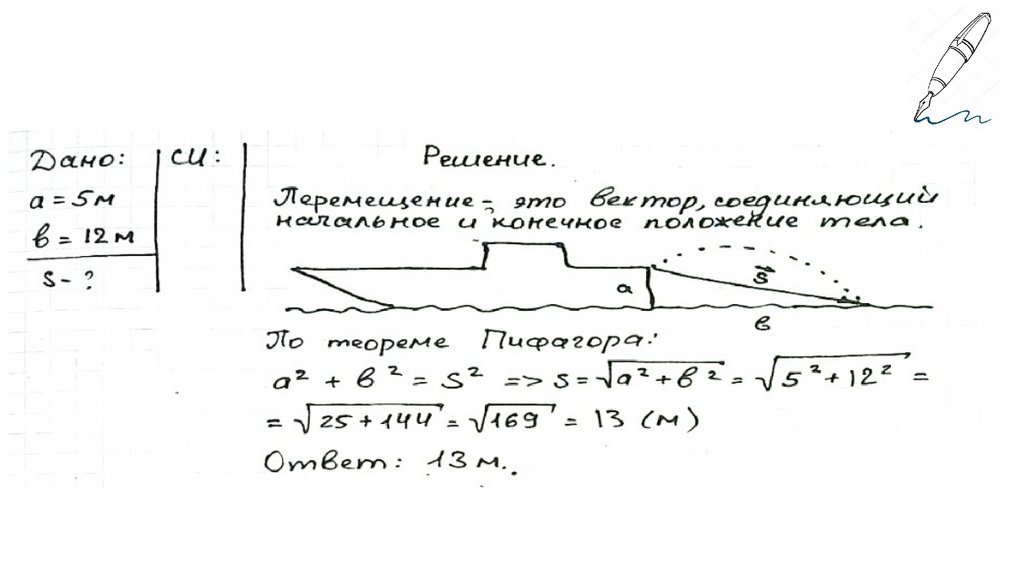
Спасательный круг, брошенный из кормы судна,возвышающейся на 5 м над уровнем воды, упал в
море на расстоянии 12 м от борта судна. Определите
модуль перемещения спасательного круга, если
траектория его движения лежит в диаметральной
плоскости судна.
9.
10. Задача
Корабль прошел по прямому пути 8км за 1,5 ч, а потом еще 2 ч двигался
в том же направлении со скоростью
30 км/ч. После чего корабль изменил
скорость и оставшиеся 10 км двигался
со скорость 20 км/ч. Определите
среднюю скорость корабля за все
время движения.
11.
Дано:Решение
Примечание: в данном случаем можно не переводить в СИ.
Средняя скорость находится как общий путь, деленный на общее время:
Ответ:.
12. Задача
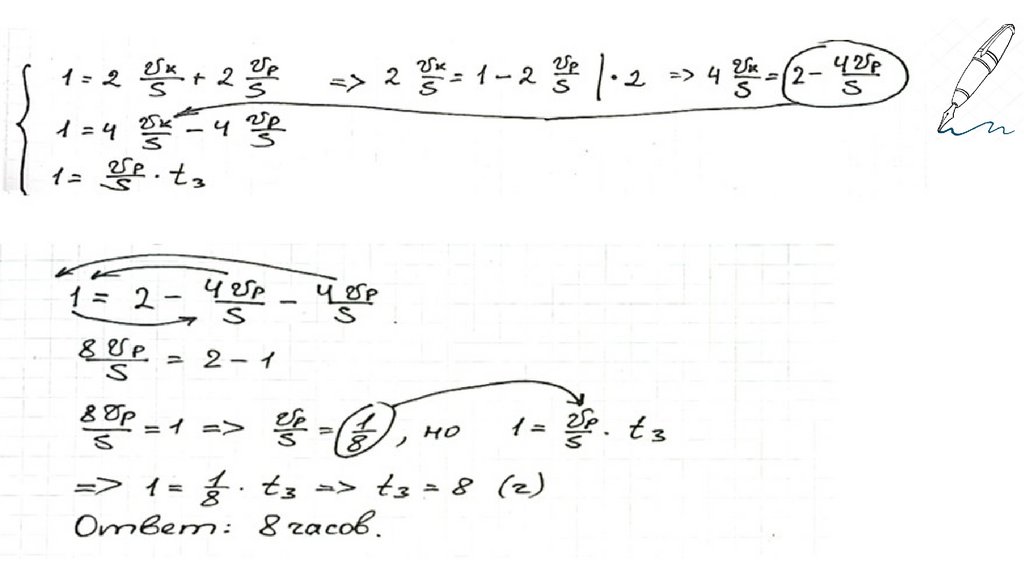
Движение катера между двумя пристанями длится 2 ч, если катердвижется по течению реки, и 4 ч, если он движется против течения.
Определите время движения по течению между этими пристанями
катера с выключенным двигателем.
13.
14.
15. Задача
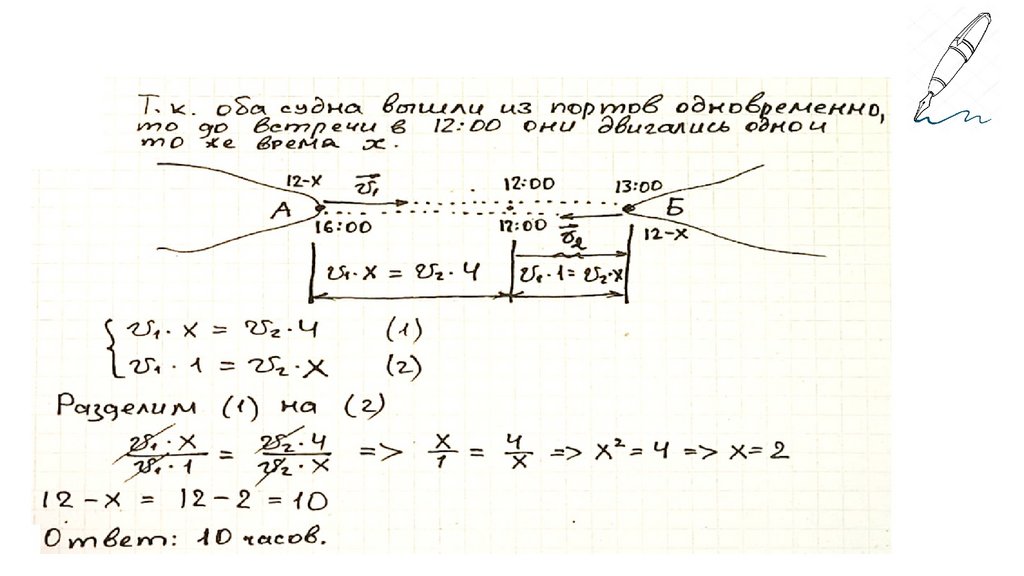
Два судна одновременно вышли из портов. Одно из них из порта Ав порт Б, другое из порта Б в порт А. Скорости судов различны. В 1200 этого же дня суда встретились, а в 13-00 одно из судов достигло
своего пункта назначения. Второе судно достигло своего пункта
назначения в 16-00. В какое время суда вышли из портов?
16.
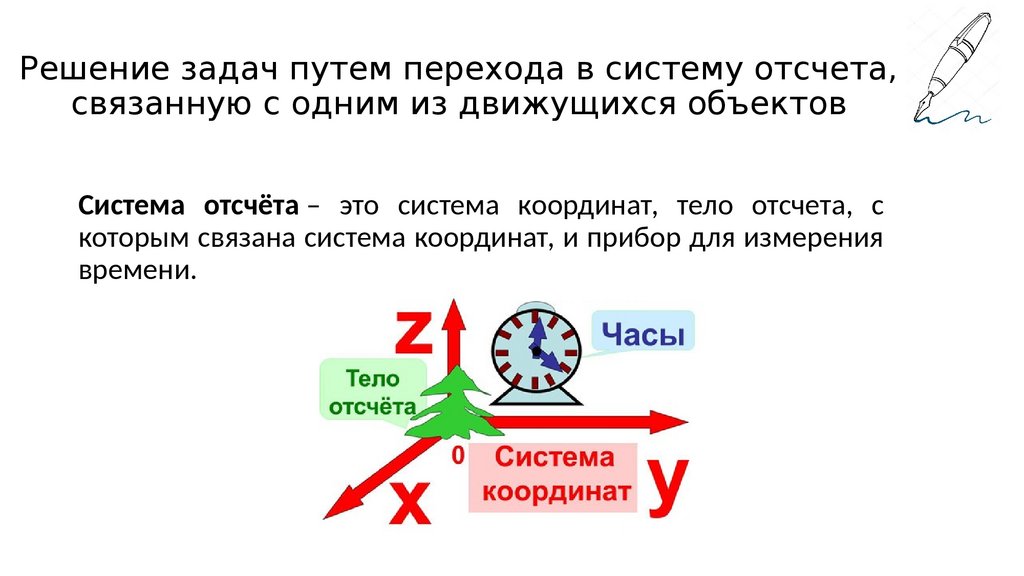
17. Решение задач путем перехода в систему отсчета, связанную с одним из движущихся объектов
Система отсчёта – это система координат, тело отсчета, скоторым связана система координат, и прибор для измерения
времени.
18. Задача
Авианосец «Адмирал Кузнецов» и крейсер «Петр Великий»,двигаясь во встречных направлениях, проходят друг мимо друга в
течение 25 с. Длина «Адмирала Кузнецова» равна 304,5 м, модуль
скорости его движения – 29 узлов. Определите модуль скорости
движения крейсера, если его длина составляет 251 м. (1 узел
считать равным 0,5 м/с).
19. Задача
Дано:.
= 304,5м.
=29узлов
=251м
СИ
0,529
Решение
Перейдем в систему отсчета, связанную авианосцем. Тогда авианосец
будем считать неподвижным, а крейсер будет двигаться относительно
авианосца со скоростью (+).
Время движения крейсера относительно авианосца будет равно времени
прохождения крейсером расстояния .
(+)
.
20.
21. Задача
Яхта отправилась из Севастополя в Ялту со скоростью 30 км/ч.Через пол часа в том же направлении отправился катер - со
скоростью 10 м/с. Определите, через какое время катер нагонит
яхту? Успеет ли катер нагнать яхту до ее прибытия в Ялту? Длину
морского пути от Севастополя до Ялты считать равным 100 км.
22.
Дано:=100км
СИ
8,3
1800 c
100000
м
Решение
Расстояние, которое успеет пройти яхта до того, как пограничный
катер отправится в погоню:
1800 c
Перейдем в систему отсчета, связанную с яхтой. Катер будет
сближаться с яхтой со скоростью . Чтобы с такой скоростью
преодолеть расстояние м потребуется время:
100000
м
За это время яхта пройдет еще расстояние:
=72940,4 (м).
Общее расстояние, пройденное яхтой, составит:
Ответ:(≈2 часа 26 минут)
23. Задача*
Танкер длиной 180 м движется со скоростью 7 узлов.Пограничный катер проходит от носа до кормы танкера и
возвращается к носу танкера за 110 с, двигаясь в обе стороны с
одинаковой по модулю скоростью. Определите скорость
движения пограничного катера. (1 узел считать равным 0,5 м/с).
24.
25.
26.
27.
28. Задача
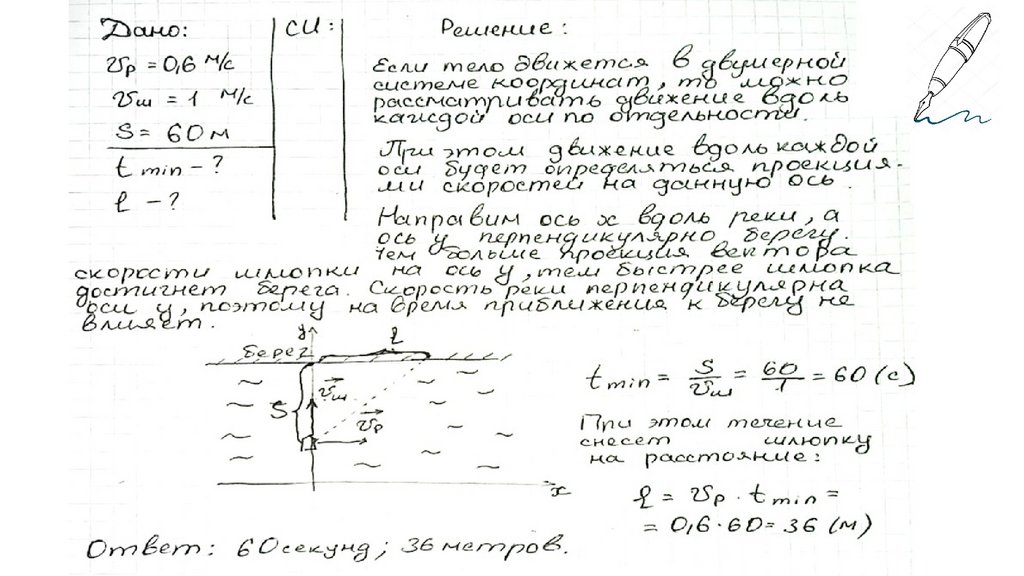
Судно терпит бедствие на реке, скорость течения которой 0,6 м/с.Спасательная шлюпка получила пробоину, вода холодная, поэтому
матрос хочет добраться до берега за кротчайшее время. Какое
потребуется время, чтобы добраться до берега, если скорость
шлюпки 1 м/с, а расстояние до берега 60м. (Определите, на
сколько течение снесет шлюпку во время переправы.)
29.
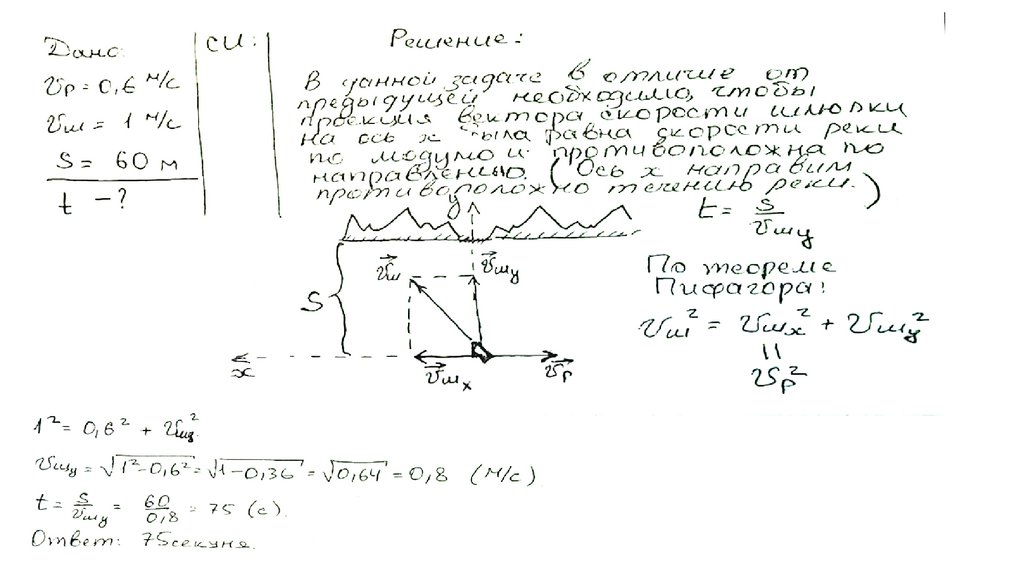
30. Задача
Судно терпит бедствие на реке, скорость течения которой 0,6 м/с.Спасательная шлюпка получила пробоину, вода холодная, поэтому
матрос хочет добраться до берега за кротчайшее время. Какое
потребуется время чтобы добраться до берега, если скорость
шлюпки 1 м/с, расстояние до берега 60м, а единственное место,
куда может причалить шлюпка, находится как раз напротив
терпящего бедствие судна.
31.
32. Задача
Механик на только купленном после первого рейса легковомавтомобиле, совершает опережение попутного грузовика. Когда
автомобиль механика опередил на несколько метров грузовик,
двигавшийся со скорость 72 км/ч по соседней полосе, механик
решил перестроится в его ряд под углом 30 градусов. Какую
минимальную скорость должна показывать стрелка спидометра
легкового автомобиля во время перестроения, чтобы сохранялась
дистанция в направлении движения между грузовиком и легковым
автомобилем? Косинус 30 градусов считайте равным 0.8660.
33.
34.
•Ускорение тела:35. Ускорение свободного падения
•Галилео Галилей первым вычислил ускорение свободного падениятел:
Мы во всех задачах для простоты расчетов будем принимать
Это приведет к погрешности 2%, но значительно упростит вычисления.
36.
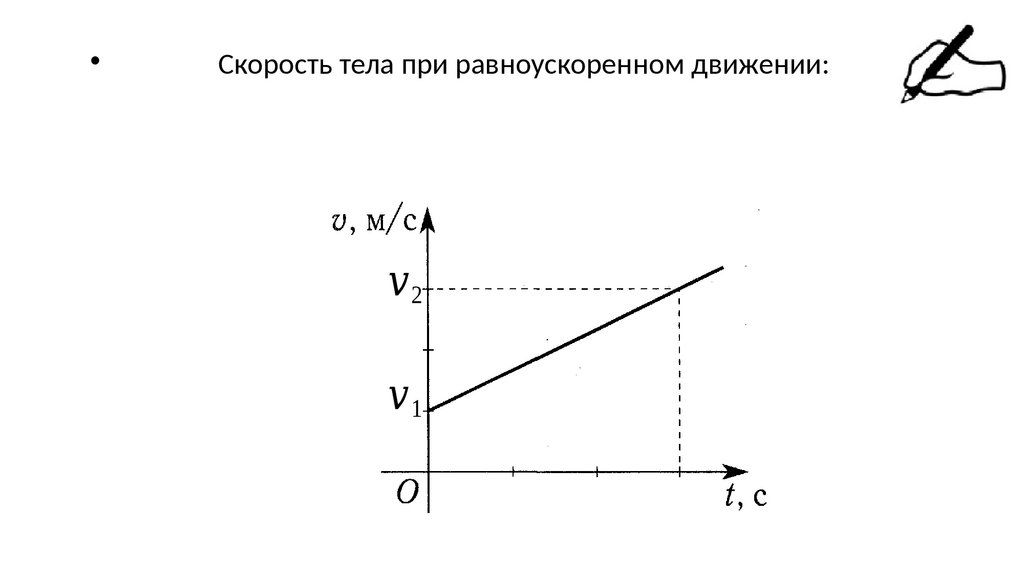
Скорость тела при равноускоренном движении:
2
1
37.
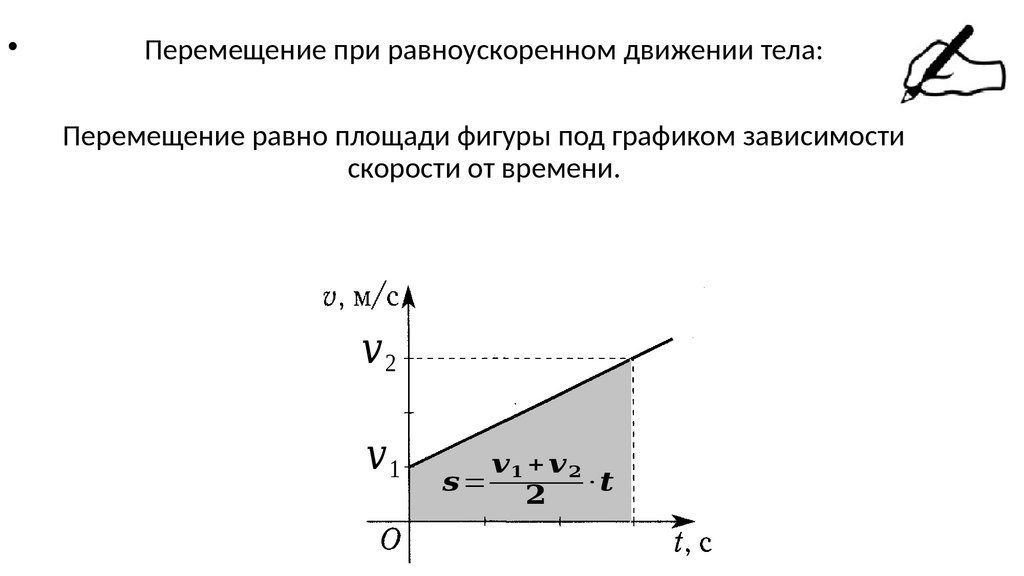
Перемещение при равноускоренном движении тела:
Перемещение равно площади фигуры под графиком зависимости
скорости от времени.
2
1
+
=
·
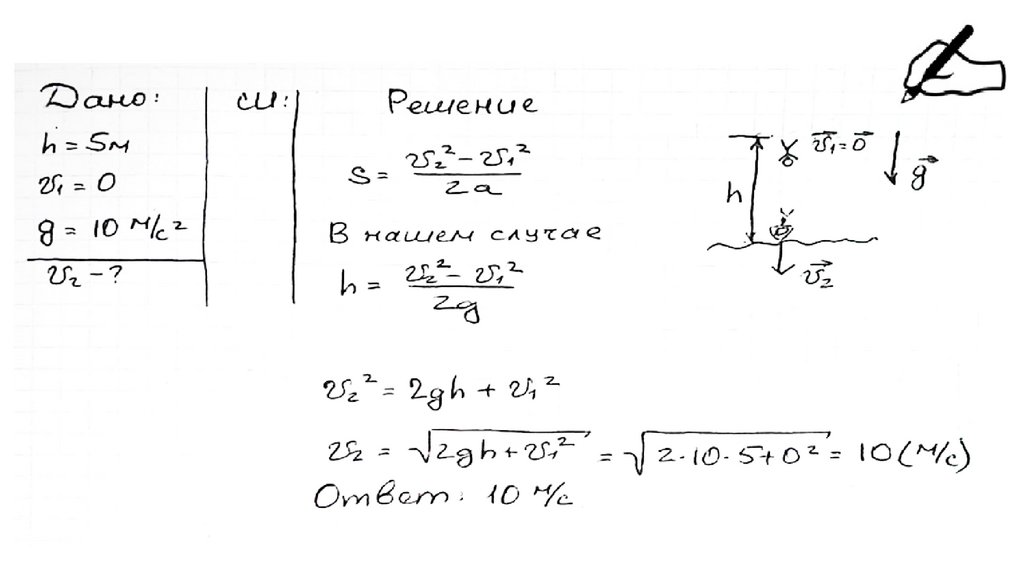
38. Задача
•Определить глубину колодца, если камень отпущенный в него,ударился об воду через 4 с. Ускорение свободного падения считать
равным 10 .
39.
40. Вычисление перемещения по заданным начальной скорости, ускорению и конечной скорости материальной точки
•⇒ (1)(2)
(1)→(2):
|·
41. Вычисление перемещения по заданным начальной скорости, ускорению и конечной скорости материальной точки (второй способ вывода
формулы)42. Задача
Какую скорость у поверхности воды будет иметь матрос, прыгнувший в водус высоты 5 м? g=10 м/с2, сопротивлением воздуха пренебречь. Начальную
скорость матроса считать равной нулю.
43.
44. Задача*
До какой максимальной высоты долетит сигнальная ракета, выпущеннаявертикально вверх со скоростью 100 м/с? Сколько времени займет ее полет
до этой высоты? g=10 м/с2.
45. Задача*
До какой максимальной высоты долетит сигнальная ракета, выпущеннаявертикально вверх со скоростью 100 м/с? Сколько времени займет ее полет
до этой высоты? g=10 м/с2
Ответ: 500м; с.
46. Задача
Задача
Легкомоторный самолет МЧС летит на высоте 100 м со скоростью 252
км/ч. Определите на каком расстоянии до спасательной шлюпки
необходимо сбросить продуктовый набор для моряков? Сопротивлением
воздуха пренебречь. Шлюпка неподвижна. g=10 м/с2.
47.
48.
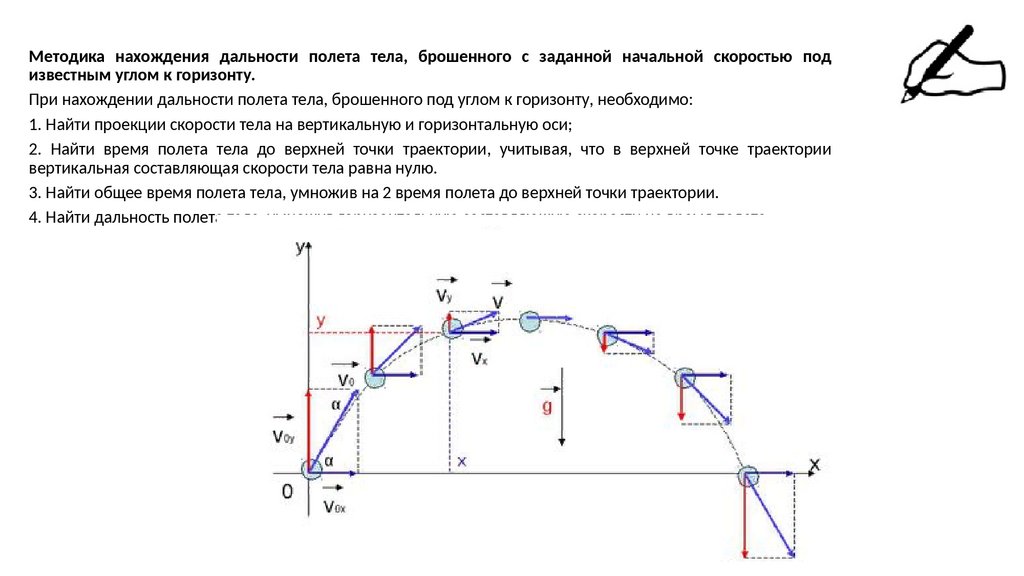
Методика нахождения дальности полета тела, брошенного с заданной начальной скоростью подизвестным углом к горизонту.
При нахождении дальности полета тела, брошенного под углом к горизонту, необходимо:
1. Найти проекции скорости тела на вертикальную и горизонтальную оси;
2. Найти время полета тела до верхней точки траектории, учитывая, что в верхней точке траектории
вертикальная составляющая скорости тела равна нулю.
3. Найти общее время полета тела, умножив на 2 время полета до верхней точки траектории.
4. Найти дальность полета тела, умножив горизонтальную составляющую скорости на время полета.
49. Задача
На каком расстоянии от орудия упадут снаряды, выпущенный подуглами 30, 45 и 60 градусов к горизонту. Начальная скорость
снарядов 853 м/с. Сопротивлением воздуха, возвышением
орудия над морем и кривизной Земли пренебречь.
50.
51.
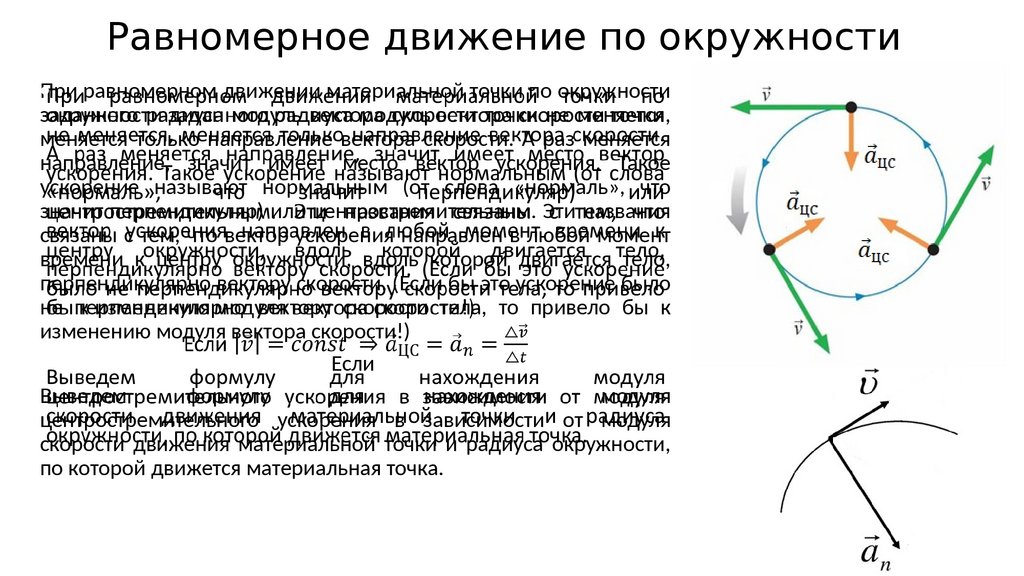
52. Равномерное движение по окружности
При• равномерном движении материальной точки по окружности
заданного радиуса модуль вектора скорости точки не меняется,
меняется только направление вектора скорости. А раз меняется
направление, значит имеет место вектор ускорения. Такое
ускорение называют нормальным (от слова «нормаль», что
значит перпендикуляр) или центростремительным. Эти названия
связаны с тем, что вектор ускорения направлен в любой момент
времени к центру окружности, вдоль которой двигается тело,
перпендикулярно вектору скорости. (Если бы это ускорение было
не перпендикулярно вектору скорости тела, то привело бы к
изменению модуля вектора скорости!)
Если
Выведем
формулу
для
нахождения
модуля
центростремительного ускорения в зависимости от модуля
скорости движения материальной точки и радиуса окружности,
по которой движется материальная точка.
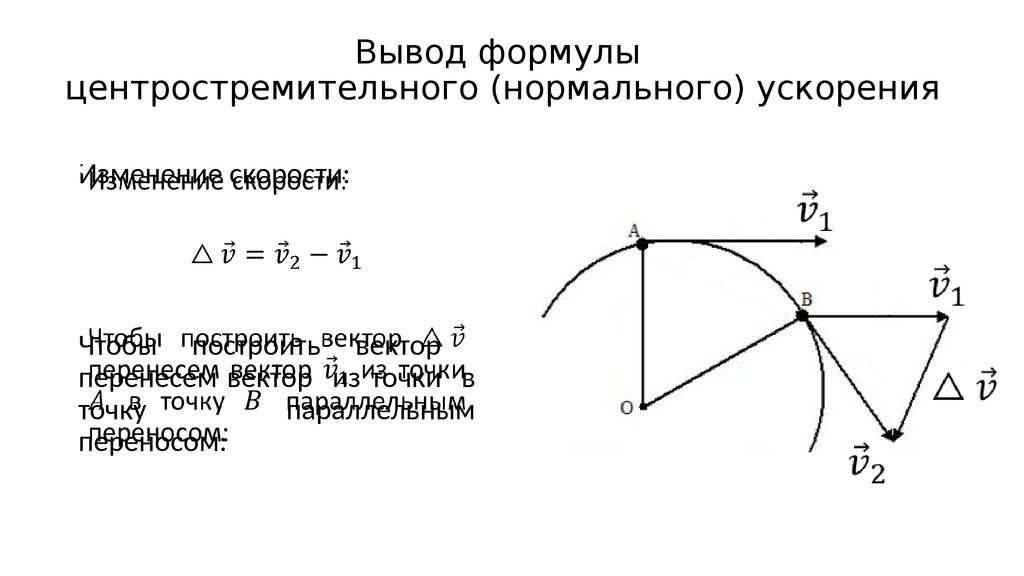
53. Вывод формулы центростремительного (нормального) ускорения
•Пусть тело равномерно двигается поокружности радиусом . За время тело
перейдет из точки в точку по дуге.
Скорость тела в точке A:
Скорость тела в точке B:
и равны по модулю, но по разному
направлены.
54.
Вывод формулыцентростремительного (нормального) ускорения
•Изменение скорости:
Чтобы построить вектор
перенесем вектор из точки в
точку
параллельным
переносом:
55. Вывод формулы центростремительного (нормального) ускорения
•Путь , пройденный телом за время ,равен длине дуги :
Если , то длина дуги примерно равна
хорде .
56. Вывод формулы центростремительного (нормального) ускорения
• вектор скорости перпендикуляренТ.к.
радиусу, то угол поворота тела равен углу
поворота вектора скорости:
Учитывая, что
можно сделать вывод:
(подобны по углам)⇒
, но
, но
57. Угловая скорость
Угловая
скорость:
- угловая скорость, ;
, - угол поворота, радиан;
– время, за которое
произошел поворот, с.
58.
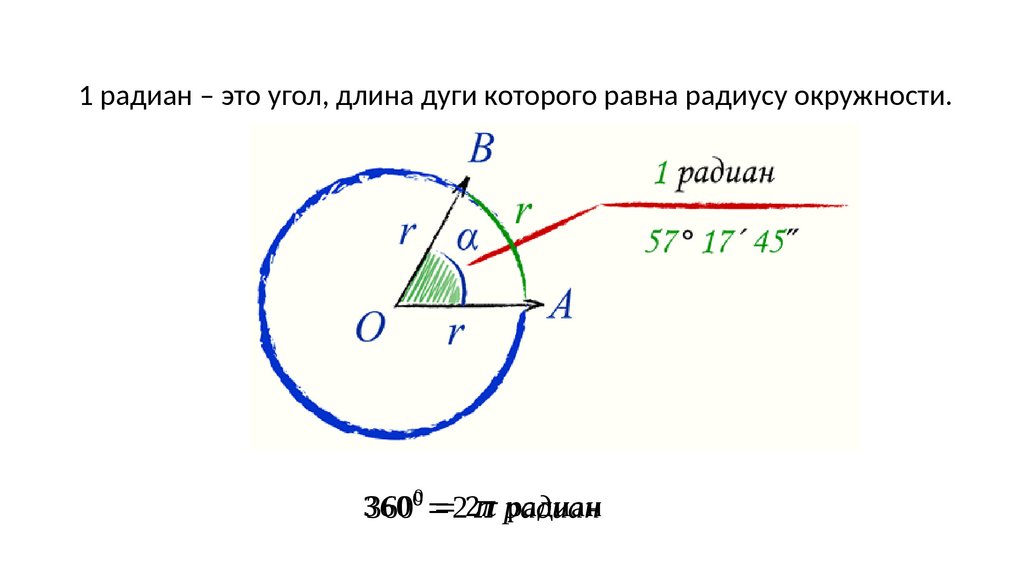
1 радиан – это угол, длина дуги которого равна радиусу окружности.0
360 =2 радиан
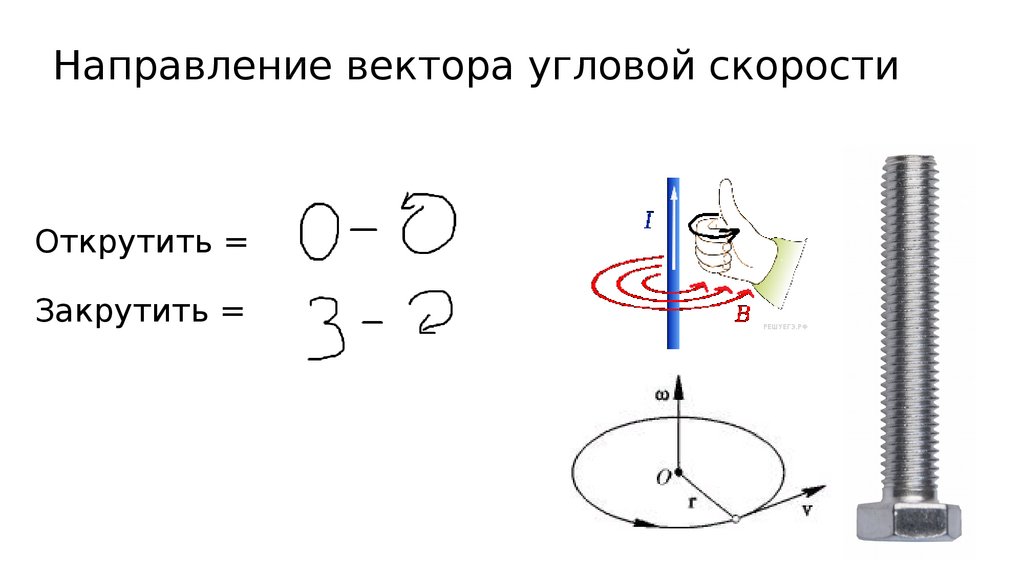
59. Открутить = Закрутить =
Направление вектора угловой скоростиОткрутить =
Закрутить =
60. Задача
Рассчитайте средние угловые скорости секундной, минутной ичасовой стрелок часов.
61.
62. Период обращения тела, частота вращения и угловая скорость
•Период вращения тела – время одного оборота.(секунда)
Частота вращения – это количество оборотов, совершаемое телом
за одну секунду.
()
1 оборот соответствует углу поворота 2π радиан, следовательно:
63. Задача
Винт судна вращается с частотой 720 оборотов в минуту. Каковаугловая скорость вращения винта?
64.
65.
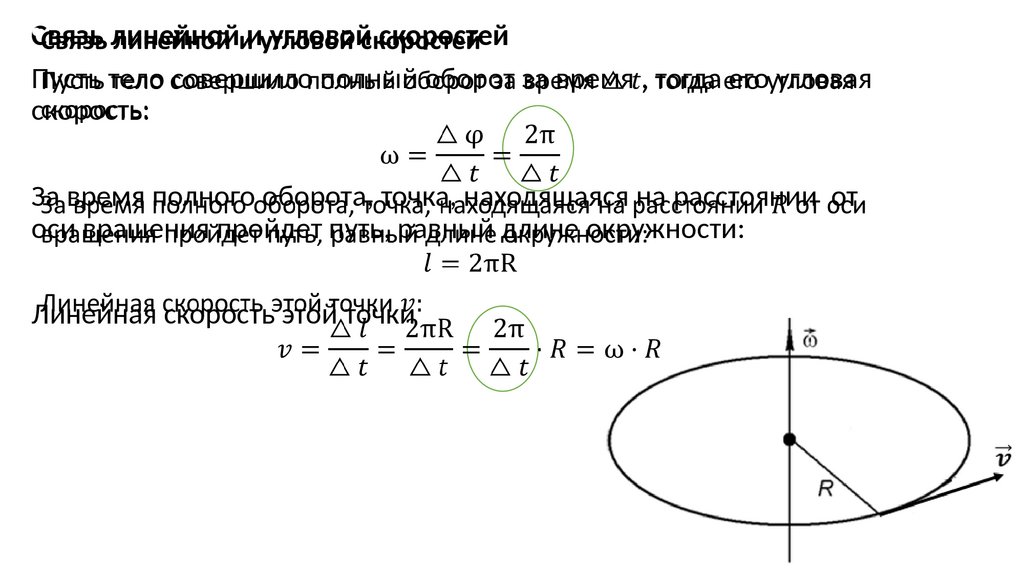
Связь
линейной и угловой скоростей
Пусть тело совершило полный оборот за время , тогда его угловая
скорость:
За время полного оборота, точка, находящаяся на расстоянии от
оси вращения пройдет путь, равный длине окружности:
Линейная скорость этой точки
66. Возрастание скорости поступательного движения точек с увеличением расстояния до оси вращения
= ·67.
Угловое
ускорение.
– угловое ускорение, ;
- начальная угловая скорость, ;
- конечная угловая скорость (измеренная через промежуток времени после
измерения )
, –изменение угловой скорости,;
– время, за которое произошло изменение угловой скорости, с.
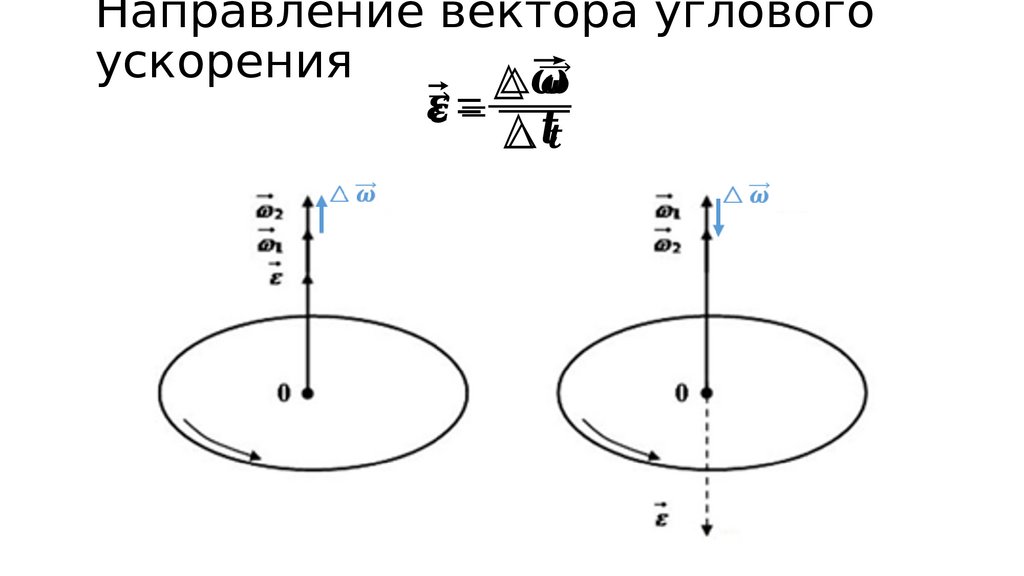
68. Направление вектора углового ускорения
△⃗⃗ =
△
69. Задача
Двигатель раскрутил корабельный винт за 20 секунд до 720оборотов в минуту. Рассчитайте угловое ускорение винта.
70.
71.
•Если тело вращается с угловым ускорением, то модуль скорости точки,расположенной на некотором расстоянии от оси вращения, будет
возрастать.
Тангенциальное ускорение, —
это компонента ускорения,
направленная по касательной к траектории движения.
Характеризует изменение только модуля скорости в
отличие
от
нормальной
компоненты
(центростремительного
ускорения),
характеризующей
изменение только направления скорости.
72.
Связь тангенциального и углового ускорения.
73.
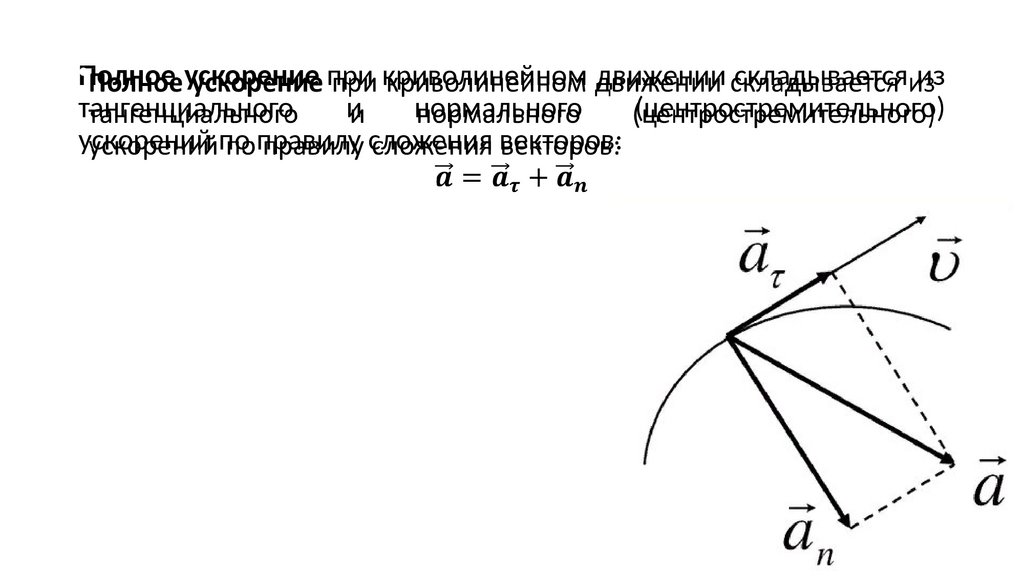
•Полное ускорение при криволинейном движении складывается изтангенциального
и
нормального
(центростремительного)
ускорений по правилу сложения векторов:
74.
• Дина́ мика (греч. δύναμις «сила, мощь») — раздел механики, в которомизучаются причины возникновения механического движения.
• Динамика поступательного движения оперирует такими понятиями,
как масса, сила, импульс, потенциальная энергия, кинетическая
энергия поступательного движения. Динамика вращательного
движения дополнительно оперирует понятиями: момент инерции,
момент силы, момент импульса, кинетическая энергия вращательного
движения.
• Основная задача динамики заключается в выяснении того, как
изменяется механическое движение тел под влиянием приложенных к
ним сил.
75.
Сила – это векторная величина, являющаяся мерой действия на данноетело других тел или полей.
Единица измерения силы в СИ– Ньютон
Сила характеризуется:
• модулем;
• направлением;
• точкой приложения.
⃗
76.
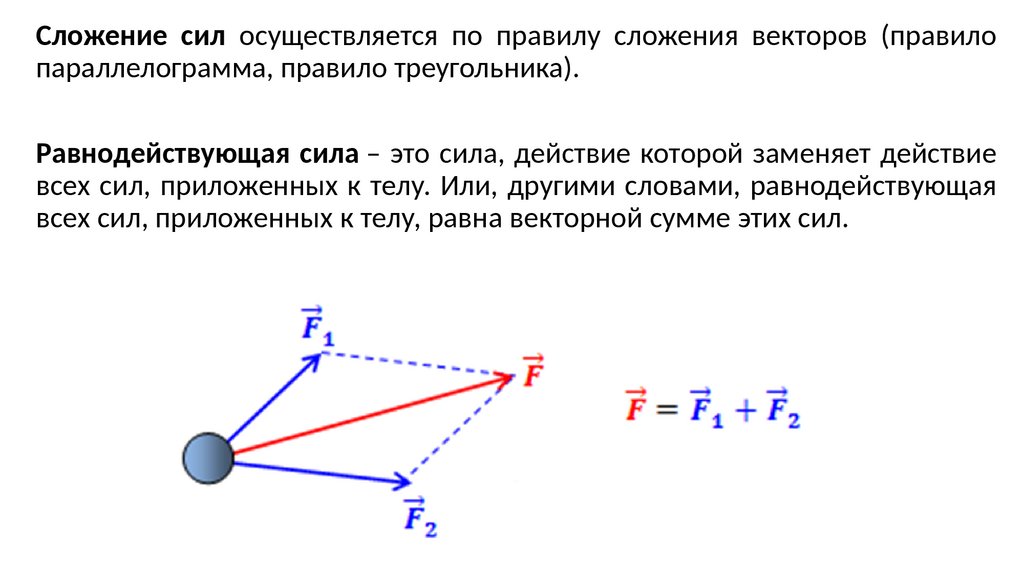
Сложение сил осуществляется по правилу сложения векторов (правилопараллелограмма, правило треугольника).
Равнодействующая сила – это сила, действие которой заменяет действие
всех сил, приложенных к телу. Или, другими словами, равнодействующая
всех сил, приложенных к телу, равна векторной сумме этих сил.
77.
Первый закон Ньютона самим Ньютоном был сформулированследующим образом: «Всякое тело продолжает удерживаться в
состоянии покоя или равномерного и прямолинейного
движения пока и поскольку оно не понуждается приложенными
силами изменить это состояние».
Системы отсчета, в которых соблюдается первый закон Ньютона
называют инерциальными.
78.
Инерция (от лат. бездеятельность)—явление сохранения состоянияпокоя или равномерного прямолинейного движения в отсутствие
внешних воздействий, а также препятствования изменению
скорости (как по модулю, так и по направлению) при наличии
внешних воздействий.
Инертность - свойство тела сохранять состояние равномерного
прямолинейного движения или покоя, когда действующие на него
силы отсутствуют или взаимно уравновешены (в механике).
79. II закон Ньютона
•Ускорение тела прямо пропорционально равнодействующей всехсил, приложенных к телу, и обратно пропорционально его массе.
- ускорение тела, ;
- равнодействующая всех сил, приложенных к телу, Н;
– масса тела, кг.
80.
Масса — физическая величина, отвечающая способностифизических тел сохранять своё поступательное движение
(инертности) , а также характеризующая количество вещества.
81. Задача
Автомобиль массой 3 тонны, двигаясь прямолинейно равноускорено, за20с уменьшил скорость своего движения от 39 до 21 км/ч. Определите
модуль равнодействующей силы, вызвавшей это изменение скорости.
82. Задача 1.
83. Задача
Определите модуль ускорения движения тела массой 2 кг, накоторое действуют представленные на рисунке силы. Модули сил:
F1=10 H; F2=F3=4 H; F4=12 H.
84.
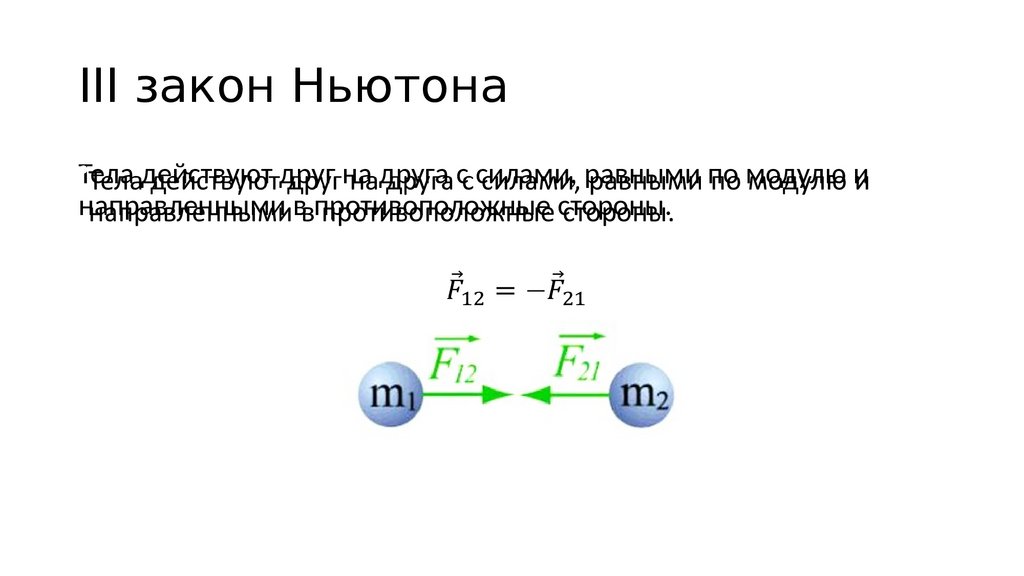
85. III закон Ньютона
•Тела действуют друг на друга с силами, равными по модулю инаправленными в противоположные стороны.
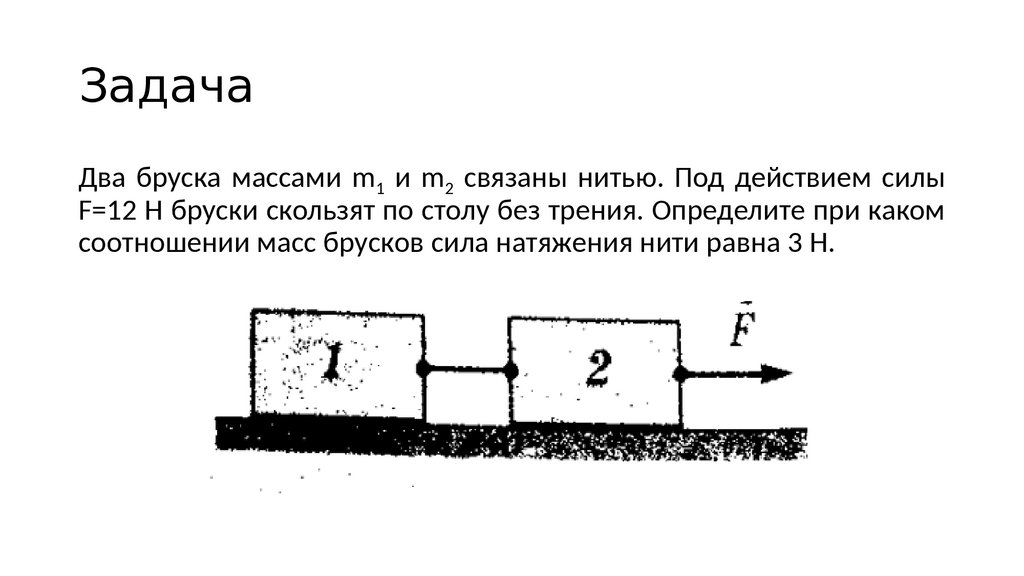
86. Задача
Два бруска массами m1 и m2 связаны нитью. Под действием силыF=12 Н бруски скользят по столу без трения. Определите при каком
соотношении масс брусков сила натяжения нити равна 3 Н.
87.
88. Основные виды сил:
• Центробежная сила• Гравитационная сила
• Сила тяжести
• Вес тела
• Сила реакции опоры
• Сила упругости
• Сила трения
89. Центробежная сила
Согласно I закону Ньютона, любому физическому телу свойственносохранять свое состояние покоя либо равномерного прямолинейного
движения до тех пор, пока на него не будет произведено какое-либо
воздействие извне.
Центробежная сила – это воздействие, которое оказывает движущееся
тело на то, что сковывает свободу его перемещения и заставляет
двигаться криволинейно.
90.
•Как было сказано ранее в разделе «Кинематика», если телодвижется равномерно по окружности, то изменение
направления
его
скорости
описывается
центростремительным ускорением:
По II закону Ньютона произведение массы тела на ускорение
численно равно силе. Значит на тело, движущееся по
окружности действует сила, которая заставляет тело менять
направление движения:
По III закону Ньютона сила действия равна силе
противодействия.
Значит
центростремительная
сила
противодействует силе инерции – центробежной силе:
Значит центробежная сила по модулю равна:
91.
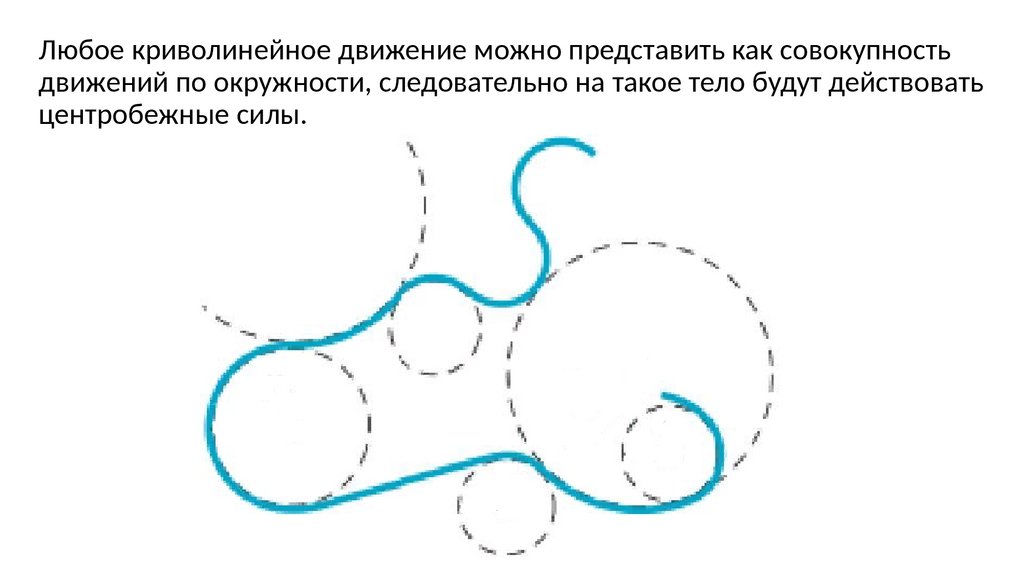
Любое криволинейное движение можно представить как совокупностьдвижений по окружности, следовательно на такое тело будут действовать
центробежные силы.
92.
Закон всемирного тяготения.Любые две материальные частицы притягиваются друг к другу с
силой, прямо пропорциональной произведению их масс и обратно
пропорциональной квадрату расстояния между ними. (Исаак
Ньютон в 1867 г.)
– сила гравитационного
взаимодействия, Н;
- массы тел, кг;
– расстояние между телами
(центрами тел), м;
– гравитационная постоянная
93.
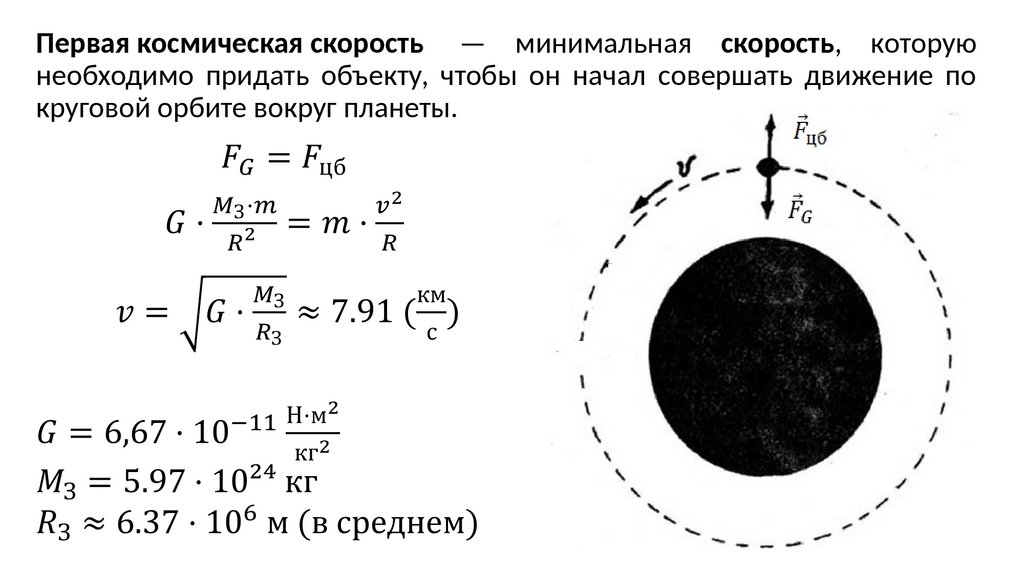
Первая космическая скорость — минимальная скорость, которуюнеобходимо придать объекту, чтобы он начал совершать движение по
круговой орбите вокруг планеты.
94.
Вращаясь со скоростью у поверхностиЗемли объект будет делать один оборот
за время равное:
(мин)
95. ГЛОНАСС и GPS
Спутник излучает сигнал с указанием точного времени его передачи. Навигаторпринимает этот сигнал и, исходя из факта, что тот двигался со скоростью 300 тысяч
километров в секунду (скорость света), рассчитывает время его движения, а значит, и
расстояние до радиопередатчика.
96. Задача Высота орбиты спутника ГЛОНАСС 19100 км, период обращения 11 часов 15 минут 44 секунды. Найдите скорость спутника.
97.
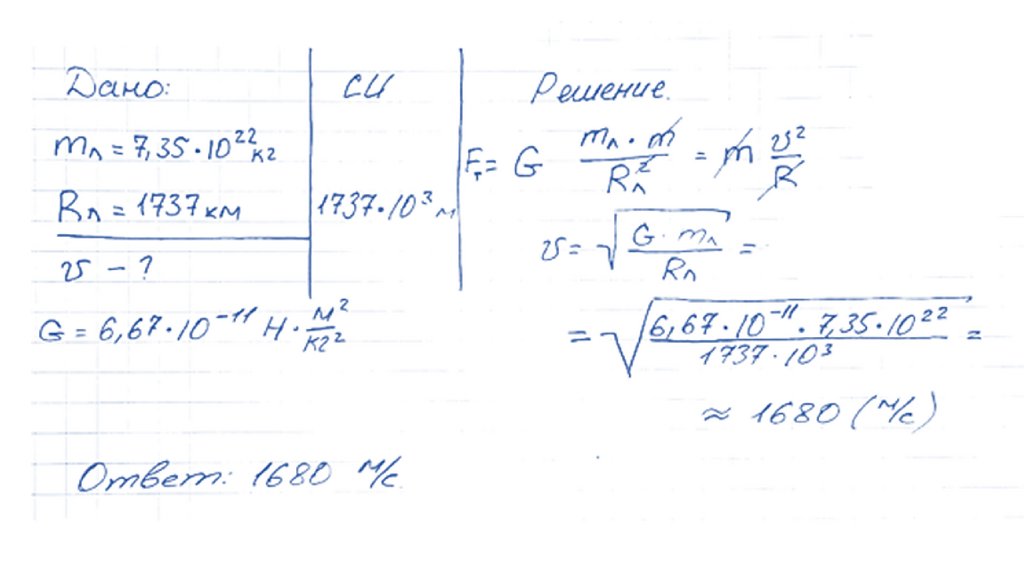
98. Задача
Масса Луны 7,35·1022 кг,радиус Луны 1737 км.
Вычислите
первую
космическую
скорость
для Луны.
99.
100.
101.
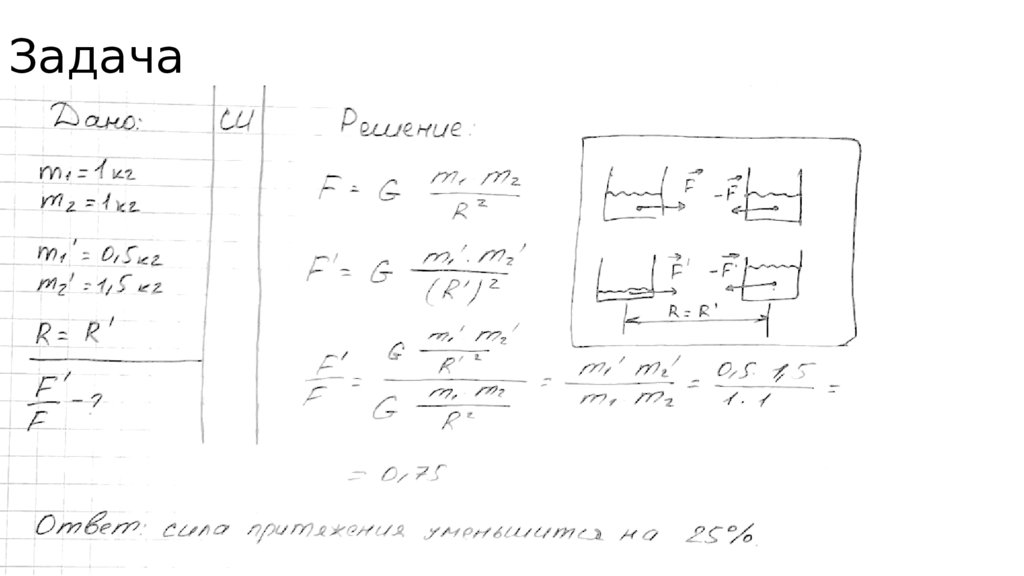
102. Задача
Расстояние между двумя банками с водой массой по 1 кг составляетнесколько метров. Из одной банки перелили в другую 0,5 кг воды и
поставили банки на те же места. Определите, во сколько раз изменилась
сила гравитационного взаимодействия между банками.
103. Задача
104. Сила тяжести
•Сила тяжести — сила, действующая на любое физическое тело, находящеесявблизи поверхности Земли или другого астрономического тела.
По определению, сила тяжести на поверхности планеты складывается из
гравитационного притяжения планеты и центробежной силы инерции, вызванной
суточным вращением планеты т.к. в связи наличие сил трения заставляет тела
вращаться вместе с планетой. Для планеты Земля центробежная сила инерции
пренебрежимо мала.
105.
Примечание:
Угловая скорость вращения Земли вокруг своей оси:
106. Ускорение свободного падения
По второму закону Ньютона:
Следовательно:
9.8
- ускорение свободного падения у поверхности
Земли.
Свободное падение – движение тела под действием силы
тяжести. В 1589 году Галилео Галилей экспериментально
показал, что все тела при свободном падении движутся с
одинаковым ускорением.
Сила тяжести в соответствии со вторым законом Ньютона:
107. Задача
Определите ускорение свободногопадения на поверхности Луны. Масса
Луны 7,35·1022 кг, радиус Луны 1737 км.
Что покажут земные пружинные весы,
на которые встанет человек массой 80
кг?
108.
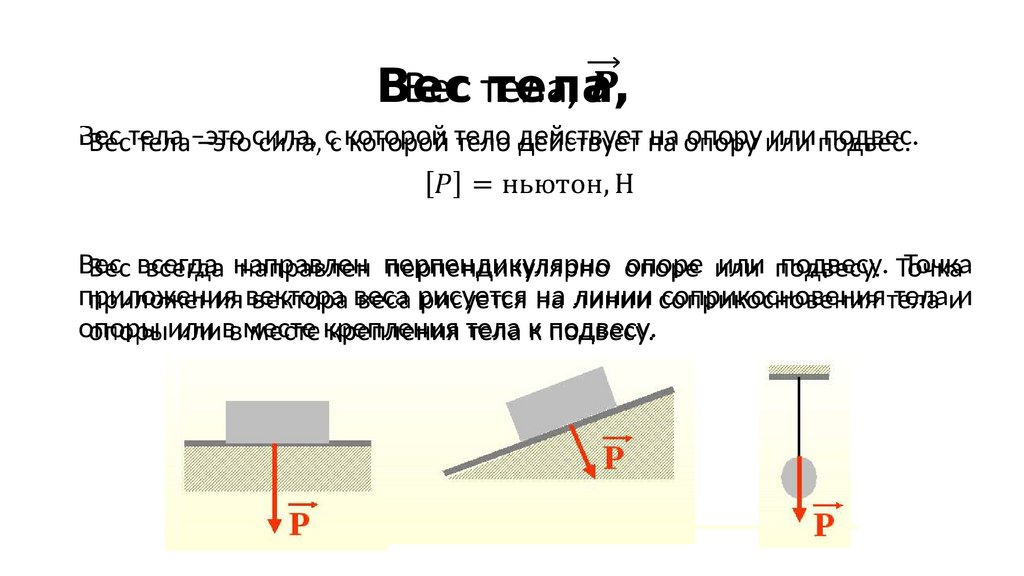
109. Вес тела, P ⃗
Вес тела,•Вес тела –это сила, с которой тело действует на опору или подвес.
Вес всегда направлен перпендикулярно опоре или подвесу. Точка
приложения вектора веса рисуется на линии соприкосновения тела и
опоры или в месте крепления тела к подвесу.
110.
•Если тело и опора неподвижны относительно земли, то веспокоящегося на опоре тела равен силе тяжести:
111. Сила реакции опоры, N ⃗
Сила реакции опоры,•По III закону Ньютона сила действия равна силе
противодействия. Силу противодействия весу
называют силой реакции опоры.
Сила
реакции
опоры
всегда
направлен
перпендикулярно опоре или подвесу. Точка
приложения вектора силы реакции опоры рисуется на
линии соприкосновения тела и опоры или в месте
крепления тела к подвесу.
112. Задача
Автомобиль движется со скоростью 54 км/ч по выпуклому мосту срадиусом кривизны 100м. Определите вес автомобиля в верхней
точке. Масса автомобиля 800 кг.
113.
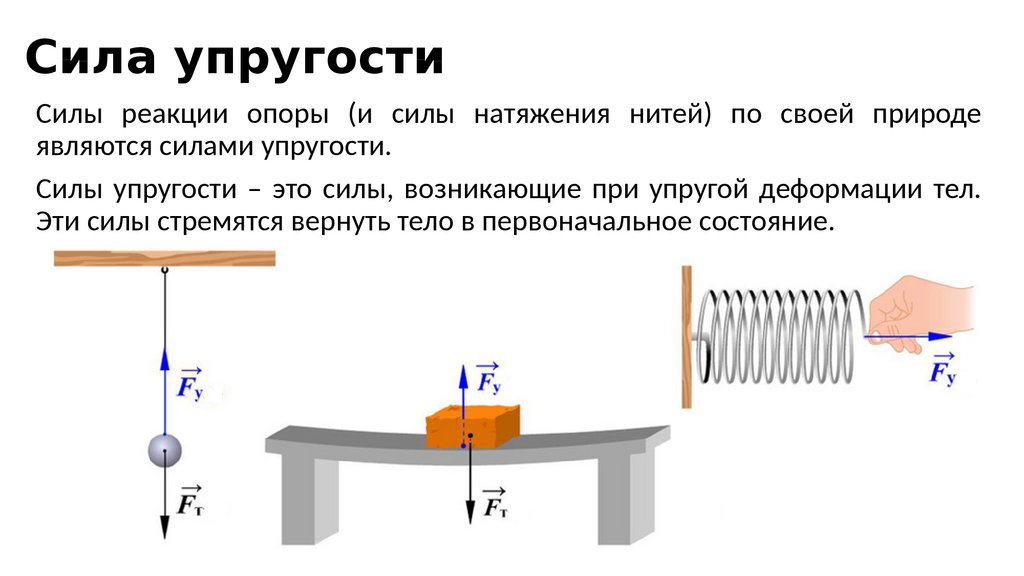
114. Сила упругости
Силы реакции опоры (и силы натяжения нитей) по своей природеявляются силами упругости.
Силы упругости – это силы, возникающие при упругой деформации тел.
Эти силы стремятся вернуть тело в первоначальное состояние.
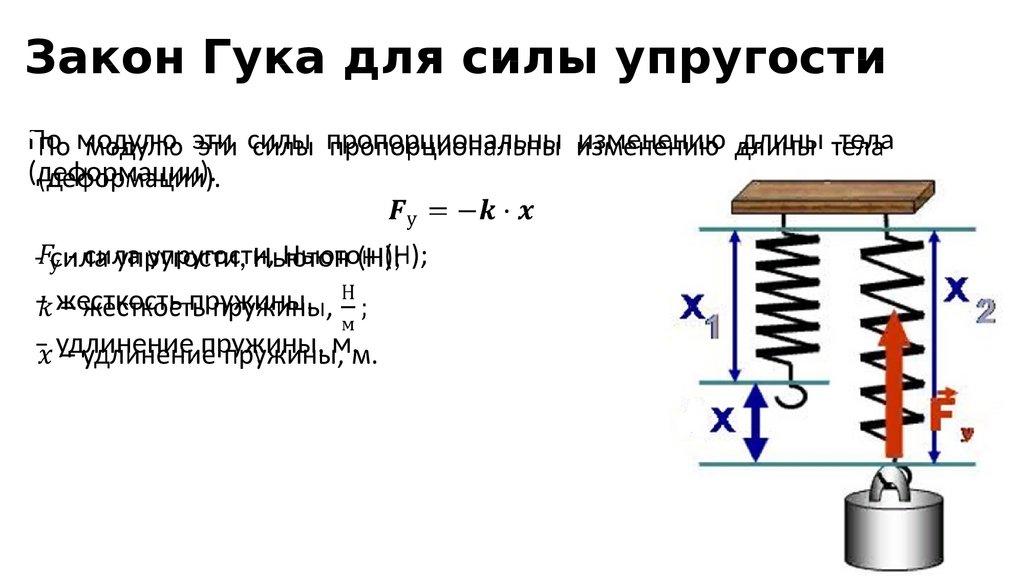
115. Закон Гука для силы упругости
•По модулю эти силы пропорциональны изменению длины тела(деформации).
- сила упругости, Ньютон (Н);
– жесткость пружины,
– удлинение пружины, м.
116. Задача
Когда масса подвешенных к пружине грузов равна 150 г, длинапружины составляет 7 см. Определите длину пружины после
увеличения общей массы грузов до 350 г, если жесткость пружины
50 Н/м.
117. Задача 9.
118. Вес тела, размещенного на опоре, движущейся с ускорением.
Пусть
лифт начал двигаться вверх или вниз с
некоторым ускорением
Тогда тело вместе с
лифтом будет двигаться с ускорением . По
второму закону Ньютона:
По III закону Ньютона тогда:
Выразим вес тела:
119.
Ведем ось Y, направленную вниз, чтобы записать
данное выражение в скалярном виде.
Если :
Если лифт движется вниз с ускорением , то вес будет
равен нулю:
120.
Если
лифт движется вниз с ускорением , то вес
будет равен:
Если лифт движется вниз с ускорением , то вес
будет равен:
121.
•Если лифт движется вверх с ускорением , то вес будет равен:122. Задача
Ракета поднимается вертикально вверх, модуль ускорения еедвижения равен 3g. Определите вес тела массой m, находящегося в
ракете.
123.
124. Задача
Определите вес человека массой 50 кг, взвешивающегося в лифте,опускающемся вертикально вниз с ускорением 3 м/с2
125.
126. Сила трения
Трение — процесс механического взаимодействия соприкасающихся телпри их относительном смещении в плоскости касания
Сила трения — это сила, возникающая при соприкосновении двух тел и
препятствующая
их
относительному
движению.
Причиной
возникновения трения является шероховатость трущихся поверхностей и
взаимодействие молекул этих поверхностей.
127.
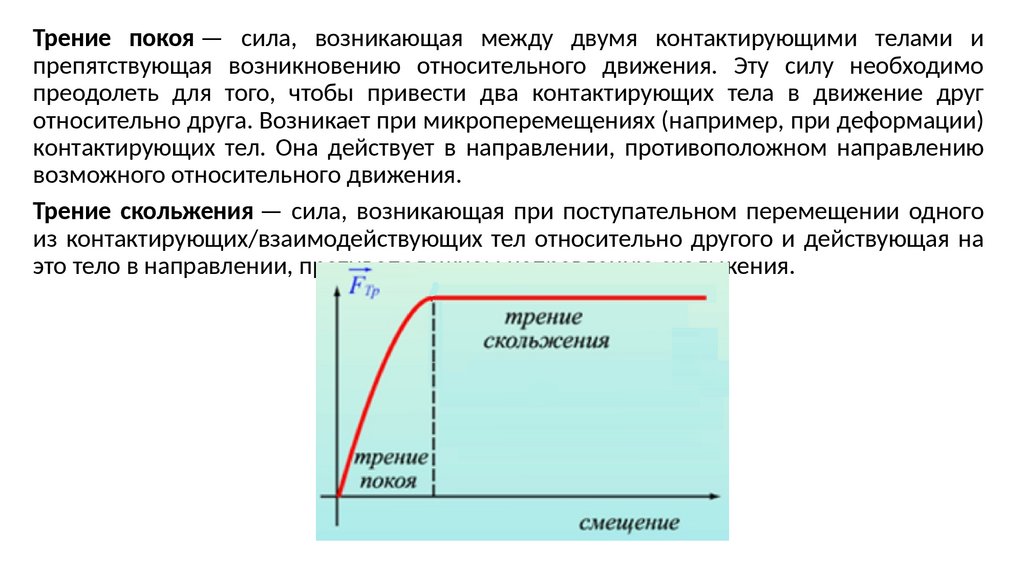
Трение покоя — сила, возникающая между двумя контактирующими телами ипрепятствующая возникновению относительного движения. Эту силу необходимо
преодолеть для того, чтобы привести два контактирующих тела в движение друг
относительно друга. Возникает при микроперемещениях (например, при деформации)
контактирующих тел. Она действует в направлении, противоположном направлению
возможного относительного движения.
Трение скольжения — сила, возникающая при поступательном перемещении одного
из контактирующих/взаимодействующих тел относительно другого и действующая на
это тело в направлении, противоположном направлению скольжения.
128. Сила трения скольжения
- сила трения скольжения, Ньютон (Н);
– коэффициент трения, безразмерная величина;
- сила реакции опоры, Ньютон.
129. Задача
Чтобы сдвинуть с места пустой ящик массой 14 кг, необходимоприложить к нему горизонтальную силу 24 Н. Определите, какая
горизонтальная сила сдвинет с места этот ящик, когда в нем будут
находиться вещи массой 28 кг.
130.
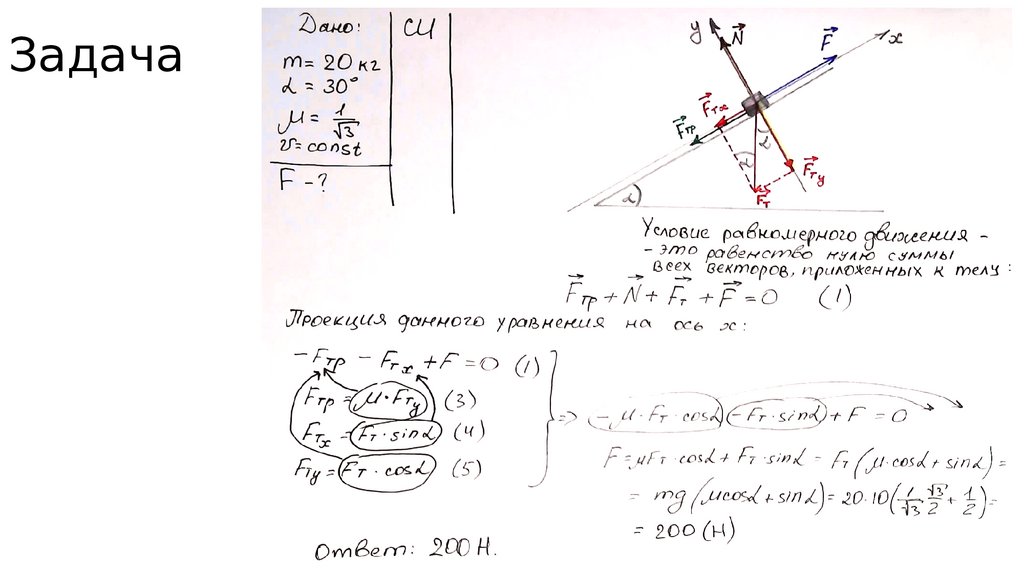
131. Задача
•Груз массой 20 кг поднимают по наклонной плоскости с угломнаклона 300, прикладывая силу в направлении движения.
Определите модуль этой силы, если груз движется равномерно, а
коэффициент трения равен .
132. Задача
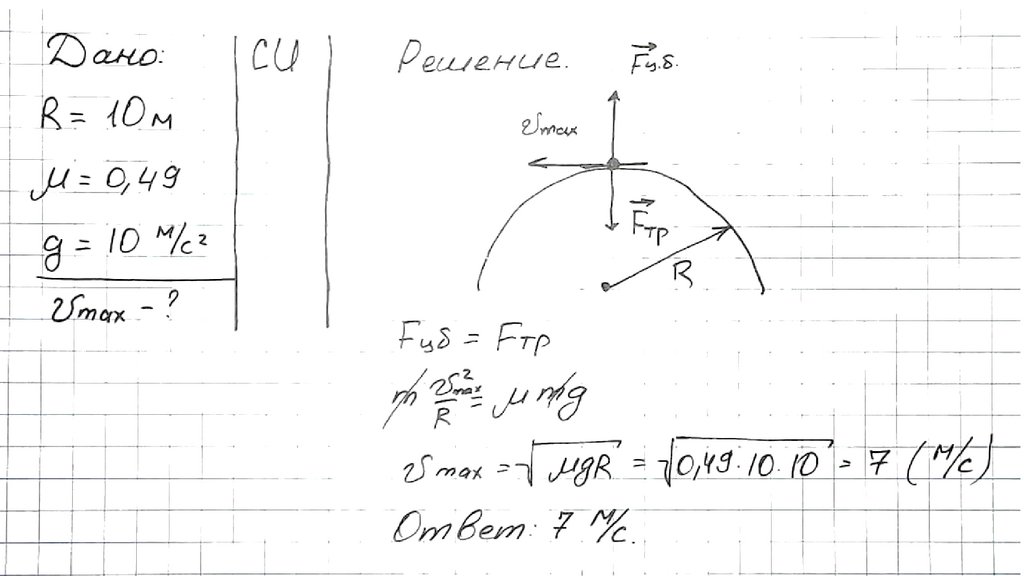
133. Задача.
•Велосипедист движется на повороте горизонтальной дороги подуге окружности радиусом 10 м. Определите максимально
возможную скорость движения велосипедиста, если коэффициент
трения между шинами и дорогой 0,49.
134.
135. ДАВЛЕНИЕ
•Действие силы на поверхность тела характеризуетсядавлением.
Давление
–
это
отношение
действующей
перпендикулярно поверхности силы, к площади
этой поверхности.
– давление, Паскаль (Па);
–
сила,
действующая
поверхности, Н;
перпендикулярно
– площадь поверхности к которой приложена сила, .
136.
1 Паскаль – это такое давление, при котором на 1 квадратный метрповерхности воздействует сила 1 Ньютон, направленная
перпендикулярно данной поверхности.
Выделяют давление твердого тела, давление жидкости и давление
газа.
Сегодня мы рассматриваем давление твердого тела. Давление
жидкостей и газов будет рассмотрено нами в следующих темах.
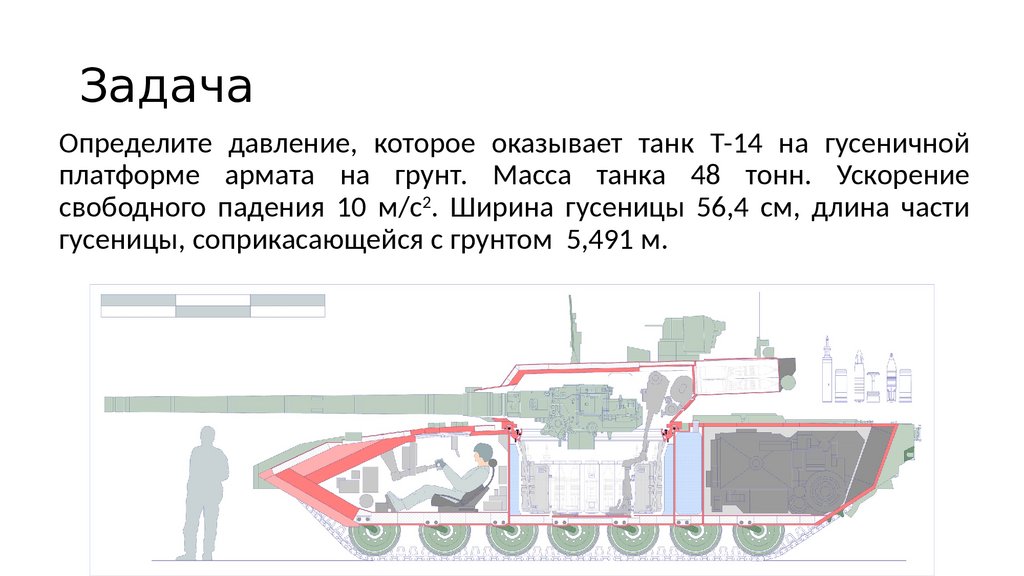
137. Задача
Определите давление, которое оказывает танк Т-14 на гусеничнойплатформе армата на грунт. Масса танка 48 тонн. Ускорение
свободного падения 10 м/с2. Ширина гусеницы 56,4 см, длина части
гусеницы, соприкасающейся с грунтом 5,491 м.
138.
139. РАБОТА ПРИ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
Работа силы – это физическая величина, характеризующая влияние
силы на перемещение тела, к которому она приложена.
– работа силы, Джоуль (Дж);
– сила, Ньютон (Н);
– перемещение тела, метр (м);
– угол между вектором силы и вектором перемещения.
140. Задача
Какую работу совершает сила трения, действующая на ящик приего перемещении на 40 см, если она постоянна и равна 5 Н?
141. Задача
Какую работу совершает сила трения, действующая на ящик приего перемещении на 40 см, если она постоянна и равна 5 Н?
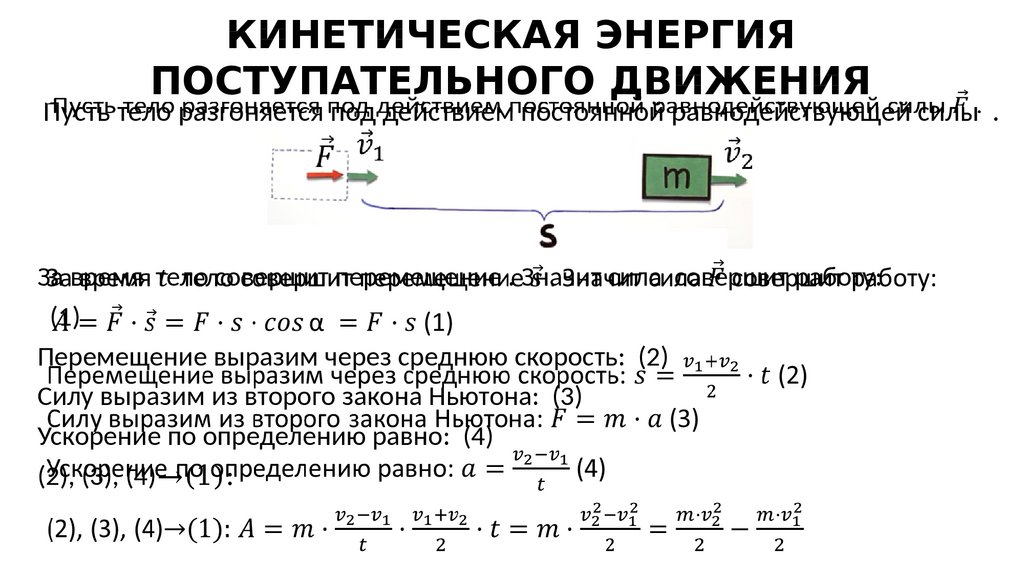
142. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
•Пусть тело разгоняется под действием постоянной равнодействующей силы .За время тело совершит перемещение . Значит сила совершит работу:
(1)
Перемещение выразим через среднюю скорость: (2)
Силу выразим из второго закона Ньютона: (3)
Ускорение по определению равно: (4)
(2), (3), (4)→(1):
143. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
•Кинетическаяэнергия поступательного
движения – это энергия, которая
определяется скоростью центра масс тела.
- кинетическая энергия поступательного
движения тела, Дж;
– масса тела ,кг;
– скорость тела,
144. Задача
Найдите тормозной путь автомобиля, двигающегося со скоростью40 км/ч; 60 км/ч; 90 км/ч. Коэффициент трения шин об асфальт
считайте равным 0.9.
145.
146. Потенциальная энергия силы тяжести
•Из кинематики известна формула:Применим эту формул для тела, отпущенного с
некоторой высоты с нулевой начальной скоростью.
Падая с высоты ускорением свободного падения
тело перед приземлением разгонится до скорости :
147. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА В ПОЛЕ СИЛЫ ТЯЖЕСТИ
•Потенциальнаяэнергия – энергия, которая
расположением взаимодействующих тел.
- потенциальная энергия, Дж;
– масса тела, кг;
– ускорение свободного падения, ;
– высота, м.
определяется
взаимным
148. Закон сохранения механической энергии
•Если в замкнутой системе не действуют силы трения и силысопротивления,
то
сумма
кинетической
и
потенциальной энергии всех тел системы остается величиной
постоянной.
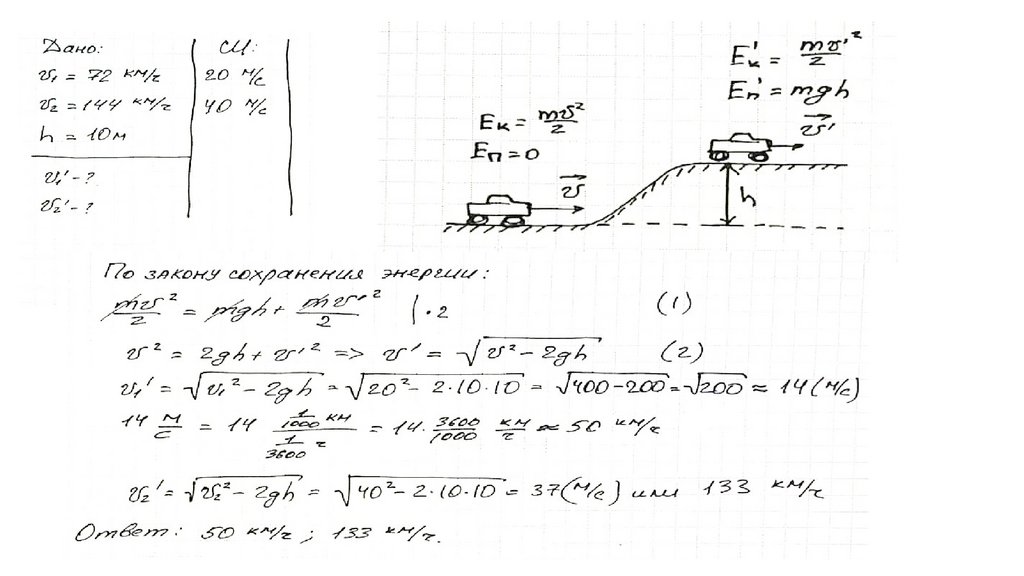
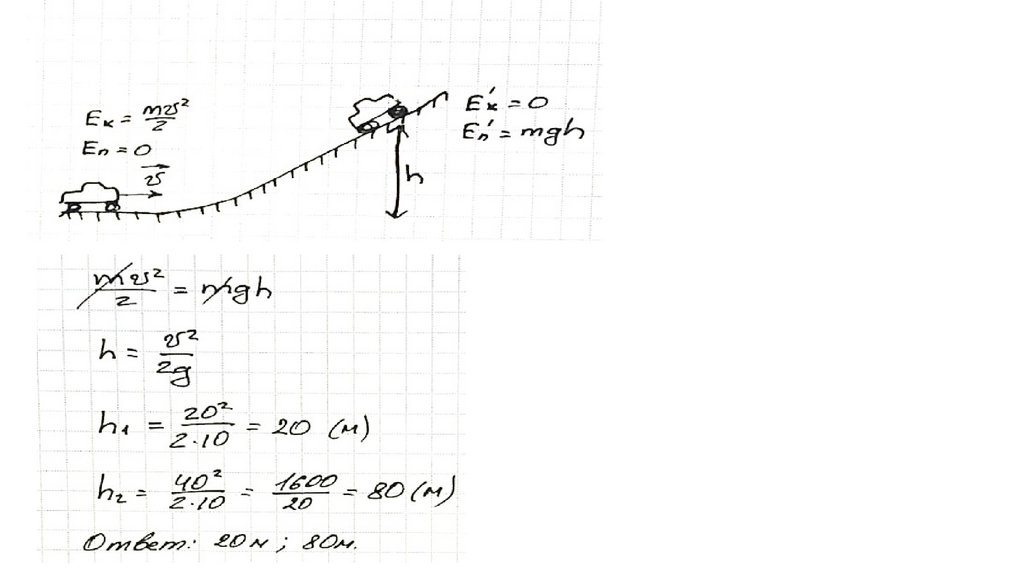
149. Задача
Водитель жигулей приближается к десяти метровому подъему соскоростью 72 км/ч, а водитель Aurus со скоростью 144 км/ч. Оба
водителя въезжают на горку на нейтральной передаче (накатом).
Какие скорости будут показывать спидометры автомобилей в
верхней точке подъема?
150.
151. Задача
В условиях предыдущей задачи найдите высоты, на которыхостановится каждый из автомобилей на тормозном тупике.
152.
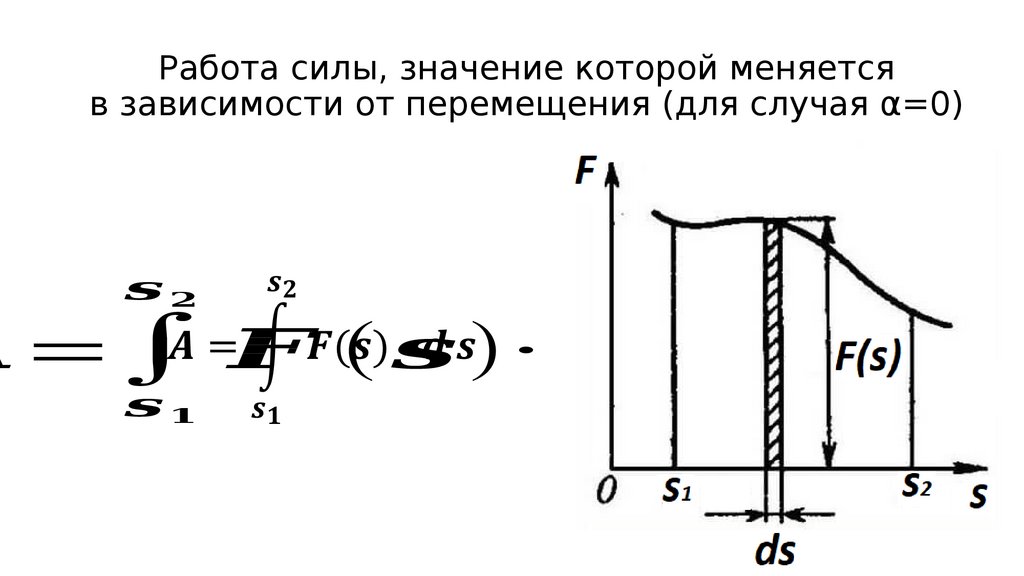
153. Работа силы, значение которой меняется в зависимости от перемещения (для случая α=0)
=∫ ( )·154. Задача
Какую работу надо совершить, чтобы сжать пружину игрушечногопистолета на 3 см, если жесткость пружины 667 Н/м? Запишите
решение с использованием интегральной формулы для работы.
155.
156. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ СЖАТОЙ ПРУЖИНЫ
•Потенциальная энергия деформированного тела – потенциальнаяэнергия обусловленная взаимным расположением частей тела.
- потенциальная энергия сжатой пружины, Дж;
– жесткость пружины, ;
– удлинение пружины, м.
157. Задача*
К концу сжатия пружины детского пружинного пистолета на 3 смприложенная к ней сила была равна 20 Н. Найти потенциальную
энергию сжатой пружины. До какой максимальной высоты долетит
присоска, если ее масса 4 грамма. Сопротивлением воздуха
пренебречь.
158.
159. КПД
•Коэффициент полезного действия (КПД) – отношение полезнойработы к затраченной работе.
– КПД, %;
- полезная работа, Дж;
- затраченная работа, Дж.
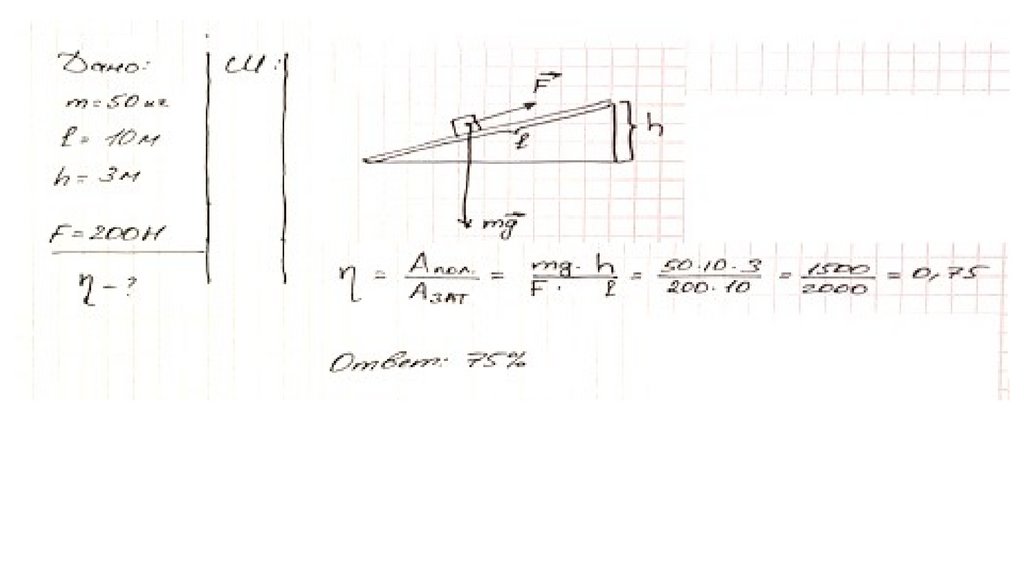
160. Задача
Определите КПД наклонной плоскости длиной 5 м и высотой 3 м,если для равномерного подъема по ней ящика массой 50 кг нужно
прикладывать силу 200 Н?
161.
162. Мощность
•Мощность – физическая величина, равная работе совершаемой вединицу времени.
– мощность, Ватт (Вт);
– работа, Дж;
– время, с.
Двигатель имеет мощность 1 Вт если он совершает работу 1 Дж за
1 секунду.
163. Задача
Какова мощность насоса способного поднять 4,5 куб. м. воды навысоту 5 м за 5 секунд. Найдите также его мощность в лошадиных
силах (1 лошадиная сила = 735,5 Вт).
164.
165. Мощность
– мощность, Ватт (Вт);
– сила, Н;
– скорость, .
166. Задача
Какова мощность электродвигателя подъемного крана, если онспособен поднимать груз массой 1 тонна со скоростью 0,5 м/с?
167.
168. Калория
Калория – количество энергии, необходимое для нагрева 1 граммаводы на 1 градус.
1 Калория ≈ 4,2 Дж
1 ккал = 1000 калорий ≈ 4200 Дж
1 Дж = 1 калория/4,2 ≈ 0,24 калории = 0,00024 ккал
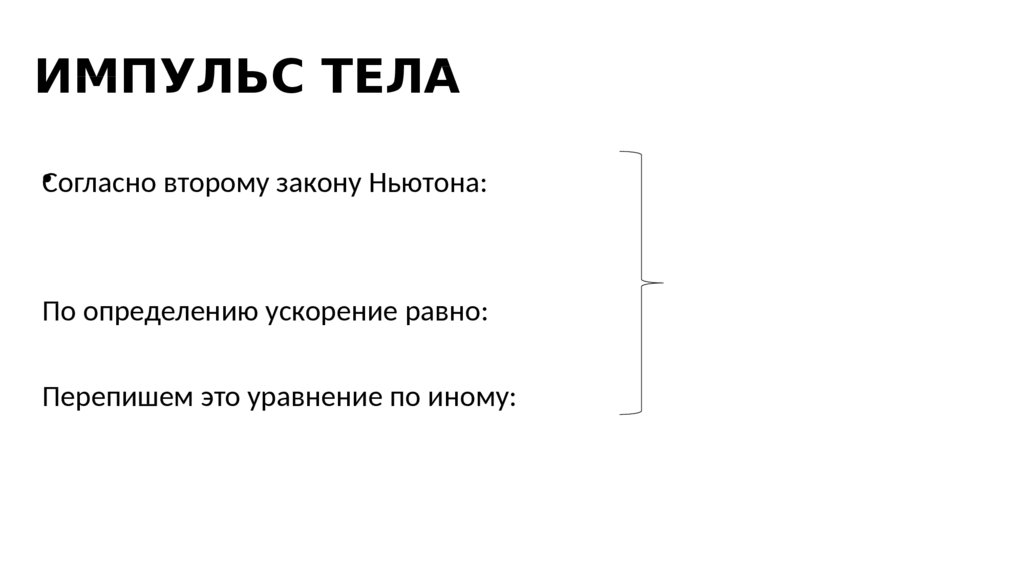
169. ИМПУЛЬС ТЕЛА
•Согласно второму закону Ньютона:По определению ускорение равно:
Перепишем это уравнение по иному:
170. ИМПУЛЬС ТЕЛА
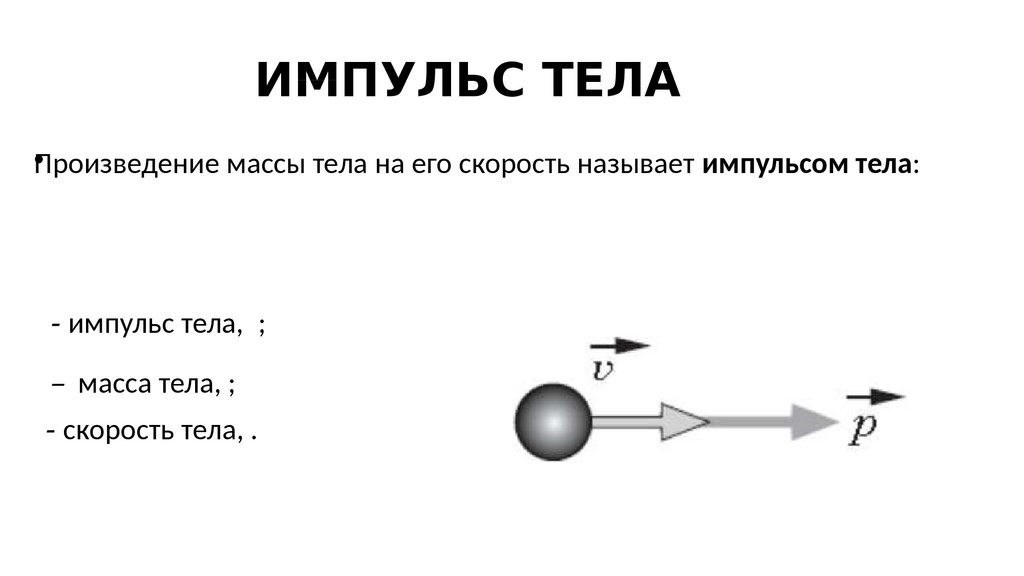
•Произведение массы тела на его скорость называет импульсом тела:- импульс тела, ;
– масса тела, ;
- скорость тела, .
171. Задача
Тело массой 5 кг движется со скоростью 10 м/с. Найдите импульсданного тела.
172.
173. ИМПУЛЬС СИЛЫ
Произведение
силы на время ее действия называется импульсом силы:
- сила, действующая на тело, Н;
– время действия силы, с.
174. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ИМПУЛЬСА
Перепишем
наше уравнение, , заменив изменение импульса
обозначением :
Уравнение, связывающее импульс силы и изменение импульса тела
называется теоремой об изменении импульса.
175. Задача
Тело массой 5 кг двигалось со скоростью 10 м/с. В течении 3 с наданное тело действовала сила 8 Н в направлении движения.
Найдите изменение импульса тела и его скорость.
176.
177. Закон сохранения импульса
ЗАКОН СОХРАНЕНИЯИМПУЛЬСА
•Векторная сумма импульсов тел, составляющих замкнутую систему
не меняется с течением времени при любых движениях и
взаимодействиях этих тел.
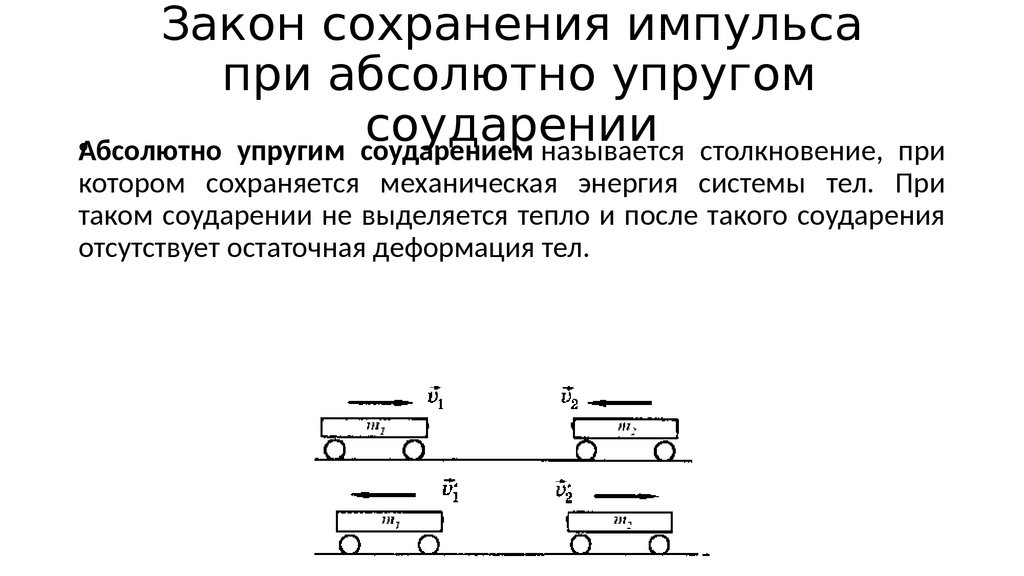
178. Закон сохранения импульса при абсолютно упругом соударении
•Абсолютно упругим соударением называется столкновение,при
котором сохраняется механическая энергия системы тел. При
таком соударении не выделяется тепло и после такого соударения
отсутствует остаточная деформация тел.
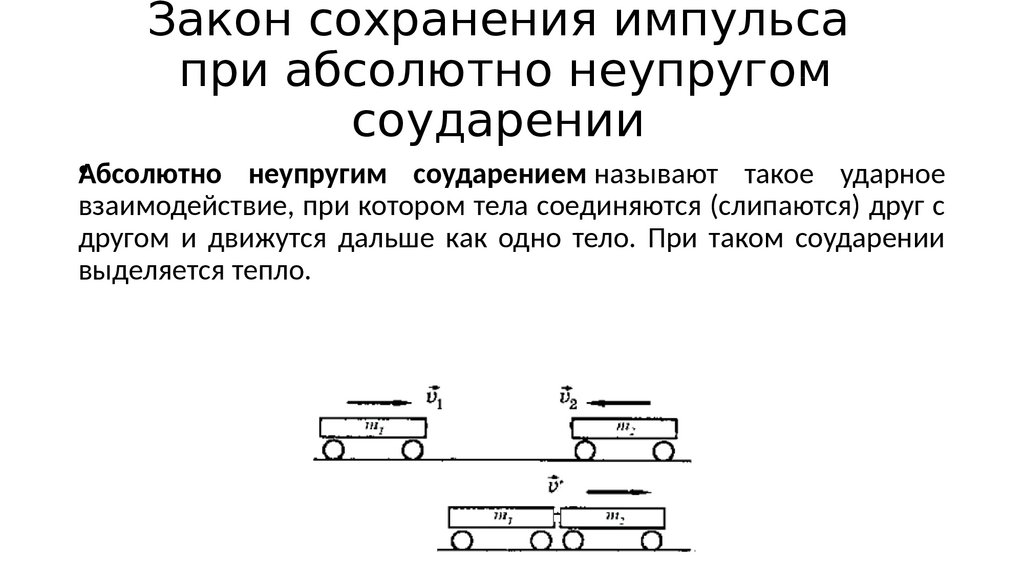
179. Закон сохранения импульса при абсолютно неупругом соударении
•Абсолютно неупругим соударением называют такое ударноевзаимодействие, при котором тела соединяются (слипаются) друг с
другом и движутся дальше как одно тело. При таком соударении
выделяется тепло.
180.
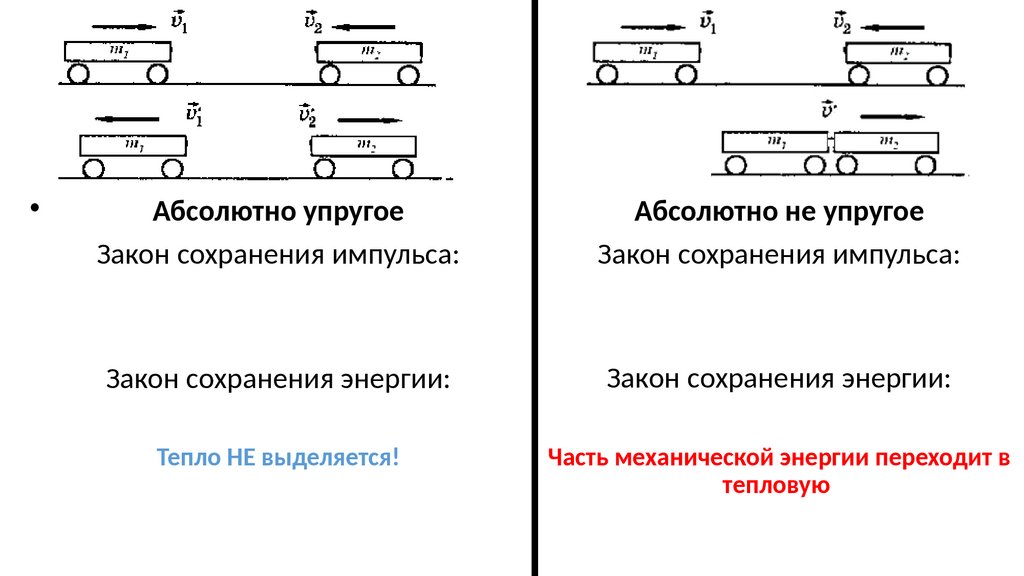
Абсолютно упругое
Закон сохранения импульса:
Абсолютно не упругое
Закон сохранения импульса:
Закон сохранения энергии:
Закон сохранения энергии:
Тепло НЕ выделяется!
Часть механической энергии переходит в
тепловую
181. Задача
Вагон массой 80 тонн, движущийся со скоростью 0,7 м/с, сцепилсяс неподвижным вагоном массой 60 тонн. Определите общую
скорость движения вагонов после сцепки.
182.
183. Задача
В условиях предыдущей задачи найти выделившееся во времясцепки тепло.
184.
185. Задача
Вагон массой 80 тонн, движущийся со скоростью 0,7 м/с, совершилабсолютно упругое соударение с неподвижным вагоном массой 60
тонн. Определите скорости движения вагонов после упругого
соударения.
186.
187.
188.
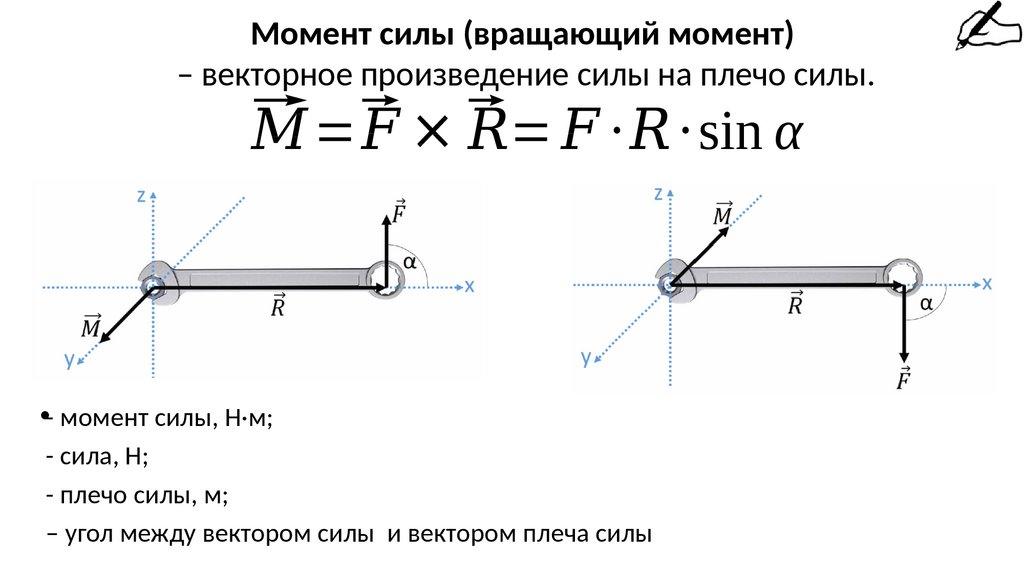
Момент силы (вращающий момент)– векторное произведение силы на плечо силы.
⃗
=⃗
⨯⃗
= · · sin α
•- момент силы, Н·м;
- сила, Н;
- плечо силы, м;
– угол между вектором силы и вектором плеча силы
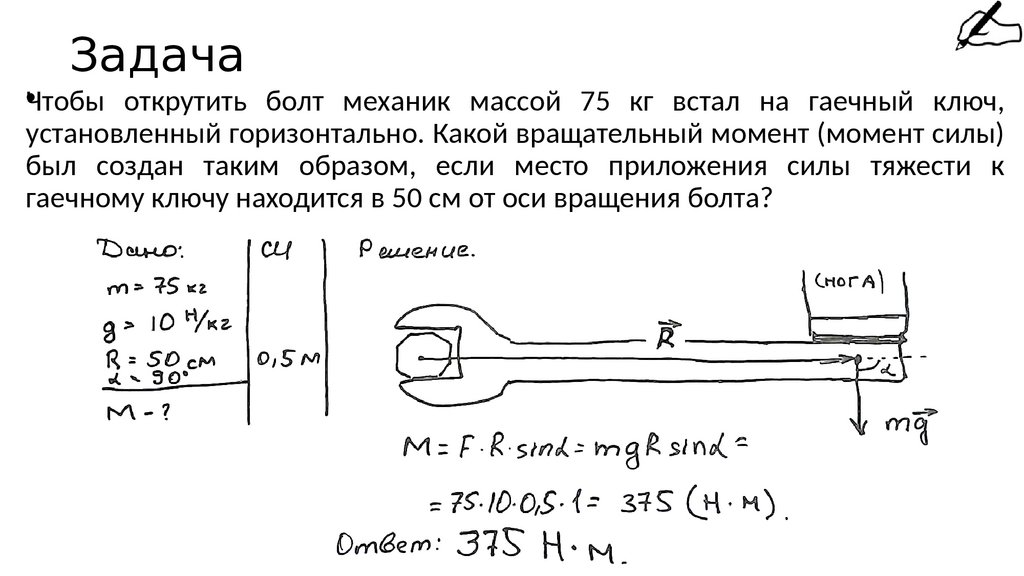
189. Задача
•Чтобы открутить болт механик массой 75 кг встал на гаечный ключ,установленный горизонтально. Какой вращательный момент
(момент силы) был создан таким образом, если место приложения
силы тяжести к гаечному ключу находится в 50 см от оси вращения
болта?
190. Задача
•Чтобы открутить болт механик массой 75 кг встал на гаечный ключ,установленный горизонтально. Какой вращательный момент (момент силы)
был создан таким образом, если место приложения силы тяжести к
гаечному ключу находится в 50 см от оси вращения болта?
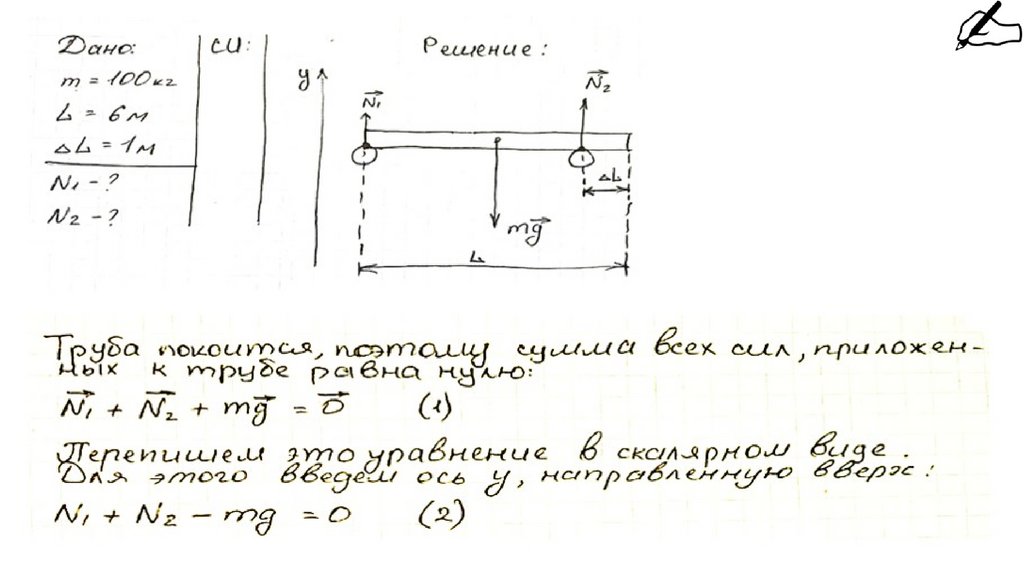
191. Задача
Труба длиной 6 м и массой 100 кг размещена горизонтально надвух опорах. Одна опора находится у левого края трубы, вторая - на
расстоянии 1 м от правого края трубы. Найдите силы реакции опор.
192.
193.
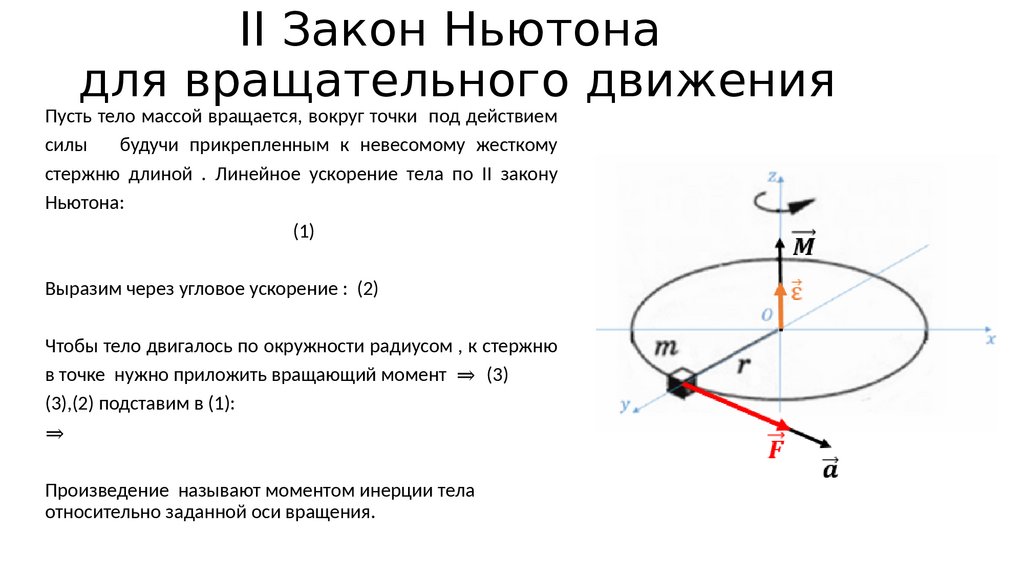
194. II Закон Ньютона для вращательного движения
Пусть тело массой вращается, вокруг точки под действиемсилы
будучи прикрепленным к невесомому жесткому
стержню длиной . Линейное ускорение тела по II закону
Ньютона:
(1)
Выразим через угловое ускорение : (2)
Чтобы тело двигалось по окружности радиусом , к стержню
в точке нужно приложить вращающий момент ⇒ (3)
(3),(2) подставим в (1):
⇒
Произведение называют моментом инерции тела
относительно заданной оси вращения.
195. Момент инерции материальной точки массой m, вращающейся по окружности радиусом r, относительно оси (z), перпендикулярной
Момент инерции материальной точки массой, вращающейся по окружности радиусом ,
относительно оси (, перпендикулярной
плоскости вращения () и проходящей через
центр данной окружности (точку ).
= ·
2
196. II Закон Ньютона для поступательного и вращательного движения
⃗⃗ =
⃗
⃗ε =
– угловое ускорение , ;
– момент силы, ;
– момент инерции тела относительно данной оси вращения, .
197. Момент инерции – сумма произведений элементарных масс, из которых состоит тело, умноженных на квадраты расстояний от них до оси
вращения2
=Σ( · )
198. Момент инерции тонкого кольца массой m и радиусом R, вращающейся относительно оси , перпендикулярной плоскости кольца и
Момент инерции тонкого кольца массой ирадиусом , вращающейся относительно оси ,
перпендикулярной плоскости кольца и
проходящей через его центр
Разделим кольцо на малые фрагменты
массами . Момент инерции одного такого
фрагмента будет равен:
Момент инерции кольца будет равен сумме
моментов инерции его фрагментов:
Но: ⇒
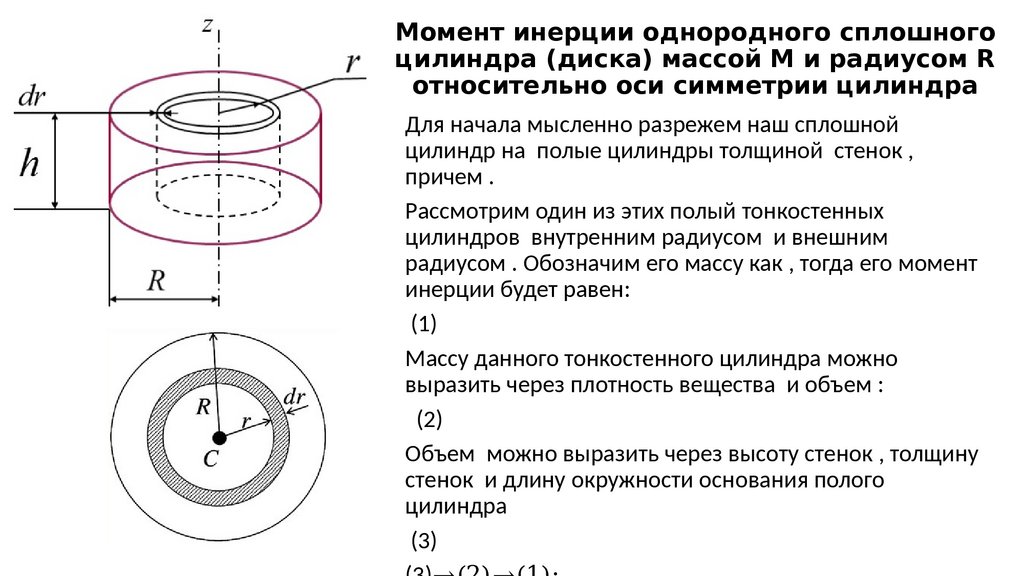
199. Момент инерции однородного сплошного цилиндра (диска) массой M и радиусом R относительно оси симметрии цилиндра
Для начала мысленно разрежем наш сплошнойцилиндр на полые цилиндры толщиной стенок ,
причем .
Рассмотрим один из этих полый тонкостенных
цилиндров внутренним радиусом и внешним
радиусом . Обозначим его массу как , тогда его момент
инерции будет равен:
(1)
Массу данного тонкостенного цилиндра можно
выразить через плотность вещества и объем :
(2)
Объем можно выразить через высоту стенок , толщину
стенок и длину окружности основания полого
цилиндра
(3)
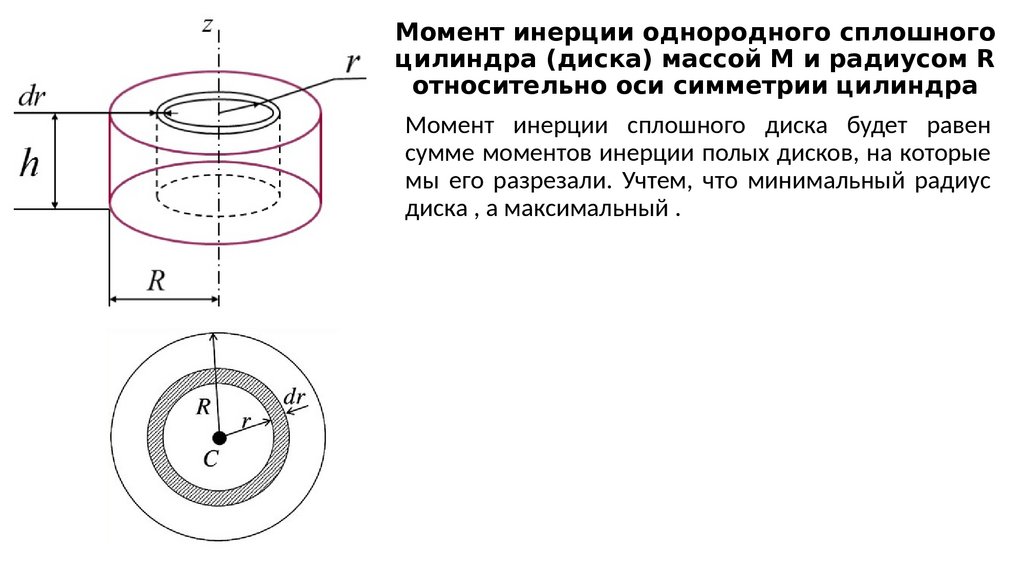
200. Момент инерции однородного сплошного цилиндра (диска) массой М и радиусом R относительно оси симметрии цилиндра
Момент инерции сплошного диска будет равенсумме моментов инерции полых дисков, на которые
мы его разрезали. Учтем, что минимальный радиус
диска , а максимальный .
201.
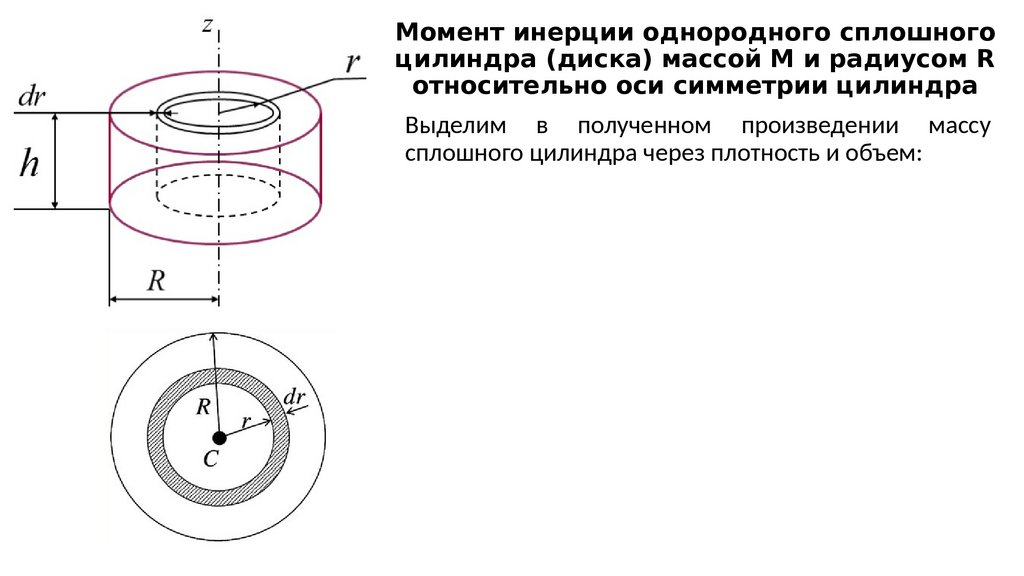
202. Момент инерции однородного сплошного цилиндра (диска) массой М и радиусом R относительно оси симметрии цилиндра
Выделим в полученном произведении массусплошного цилиндра через плотность и объем:
203. Задача
Рассчитать момент инерции сплошного диска массой 5 кг ирадиусом 20 см относительно оси, перпендикулярной плоскости
диска и проходящей через его центр.
204.
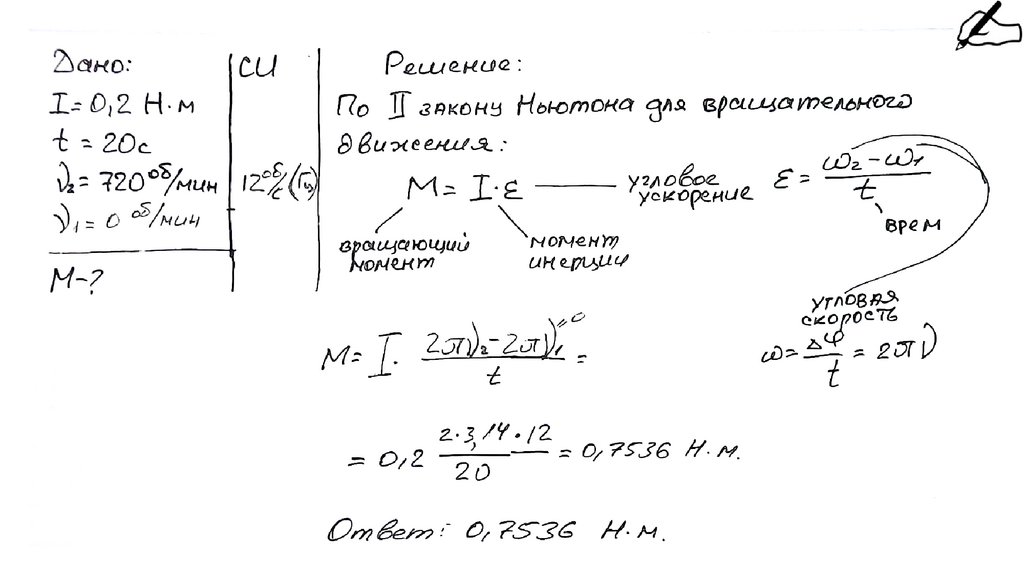
205. Задача
Двигатель раскрутил корабельный винт с моментом инерции 0.2кг·м2 за 20 секунд до 720 оборотов в минуту. Рассчитайте
вращающий момент двигателя. Винт не был погружен в воду.
Сопротивлением воздуха пренебречь.
206.
207. Момент инерции однородного стержня длиной l и массой m относительно оси, проходящей через его центр и перпендикулярной
Момент инерции однородного стержня длинойи
массой относительно оси, проходящей через его центр
и перпендикулярной плоскости вращения стержня
Выделим
на расстоянии
от оси вращения
фрагмент малой длины и массой . Момент
инерции этого малого фрагмента:
Момент инерции стержня:
208. Теорема Штейнера
Моментинерции тела массы
относительно
произвольной оси равен сумме момента инерции
этого тела относительно оси, параллельной данной и
проходящей через центр масс тела, и произведения
массы тела на квадрат расстояния между осями.
- момент инерции тела массы
относительно
произвольной оси,
- момента инерции этого тела относительно оси,
параллельной данной и проходящей через центр
масс тела, ;
– масса тела, кг;
– расстояние между осями, м.
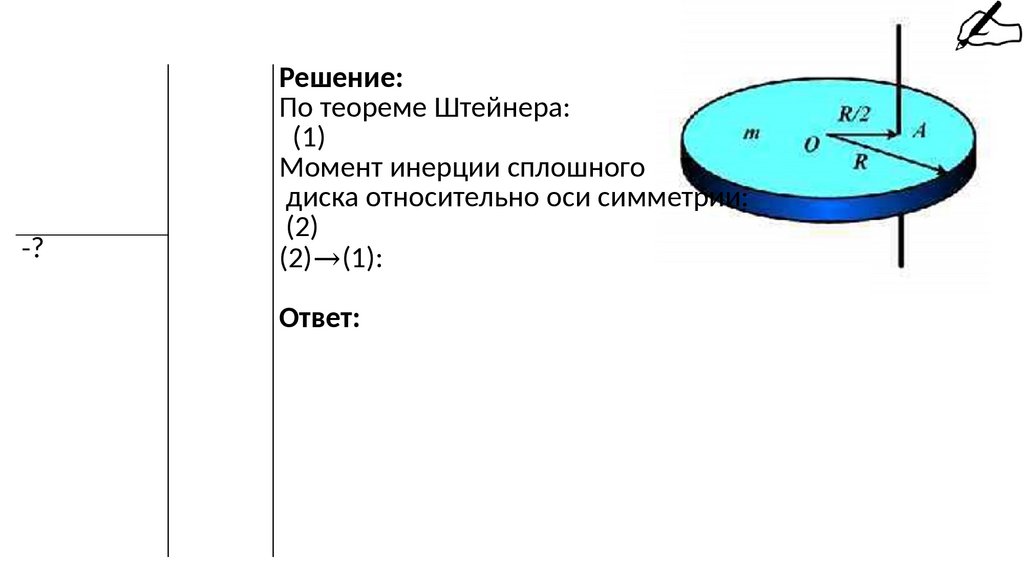
209. Задача
Найти момент инерции сплошного диска массой 5 кг и радиусом 20см относительно оси, параллельной оси симметрии диска и
смещенной на расстояние 10 см относительно нее.
210.
-?Решение:
По теореме Штейнера:
(1)
Момент инерции сплошного
диска относительно оси симметрии:
(2)
(2)→(1):
Ответ:
211. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
- кинетическая энергия вращательного движения, Дж;
– момент инерции тела, ;
– угловая скорость вращения тела, .
212. Момент импульса, Закон сохранения момента импульса
213.
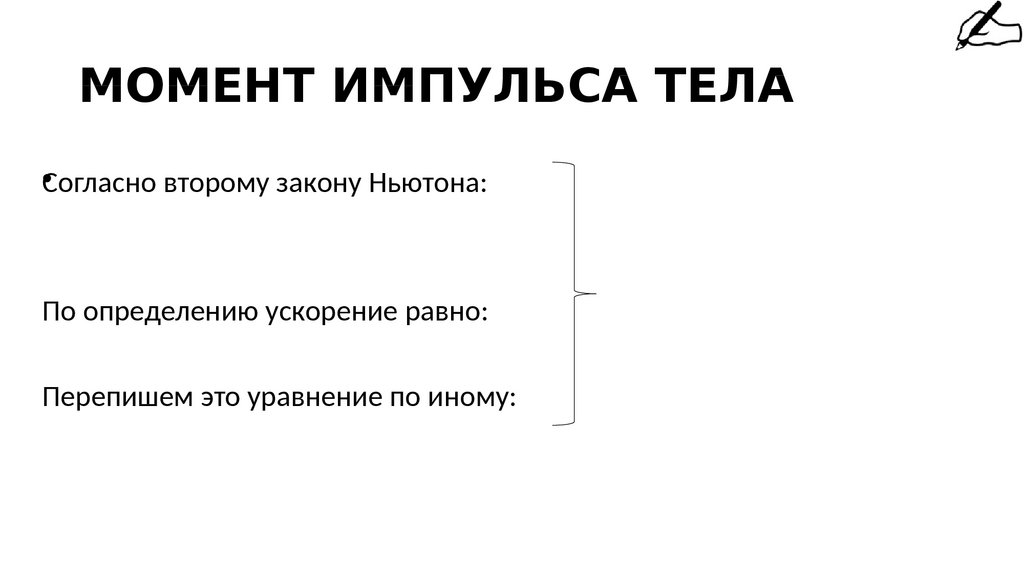
МОМЕНТ ИМПУЛЬСА ТЕЛА•Согласно второму закону Ньютона:
По определению ускорение равно:
Перепишем это уравнение по иному:
214. МОМЕНТ ИМПУЛЬСА ТЕЛА
•Произведение момента инерции тела на его угловуюскорость называется моментом импульса тела:
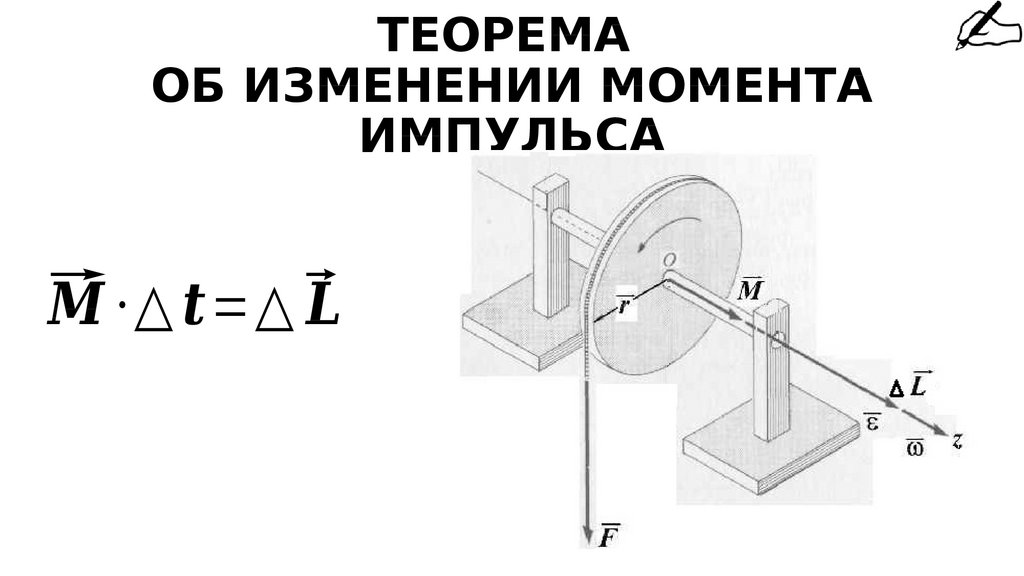
215. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА ИМПУЛЬСА
⃗· △ =△ ⃗
216. Закон сохранения МОМЕНТА импульса
ЗАКОН СОХРАНЕНИЯ МОМЕНТАИМПУЛЬСА
•Векторная сумма импульсов тел, составляющих замкнутую систему
не меняется с течением времени при любых движениях и
взаимодействиях этих тел.
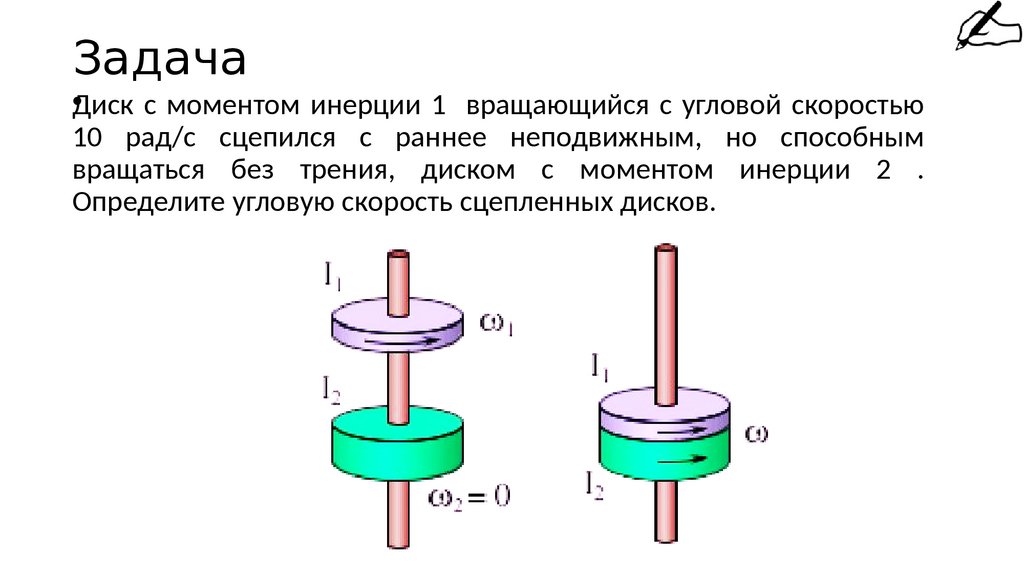
217. Задача
Диск
с моментом инерции 1 вращающийся с угловой скоростью
10 рад/с сцепился с раннее неподвижным, но способным
вращаться без трения, диском с моментом инерции 2 .
Определите угловую скорость сцепленных дисков.
218.
219.
220. ГИРОСКОП
Гироскоп – массивное симметричное тело,вращающееся вокруг своей оси симметрии.
Основное свойство вращающегося тела –
стремление сохранить положение оси
вращения
221. ПРЕЦЕССИЯ ГИРОСКОПА
Прецессия гироскопа – отклонение оси вращения гироскопа внаправлении перпендикулярном направлению воздействия на ось.
⃗
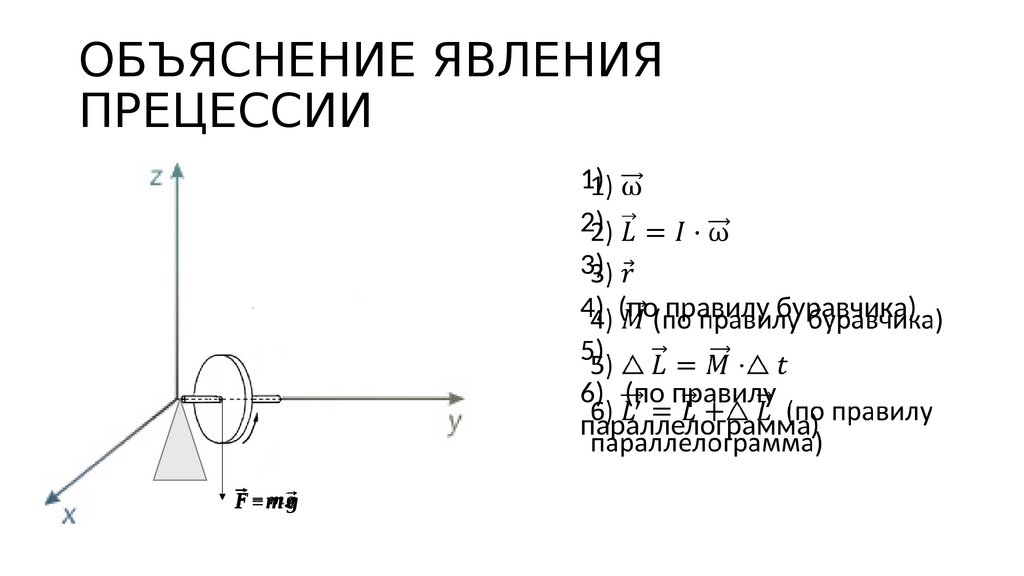
222. ОБЪЯСНЕНИЕ ЯВЛЕНИЯ ПРЕЦЕССИИ
1)2)
3)
4) (по правилу буравчика)
5)
6) (по правилу
параллелограмма)
⃗
= ⃗
223. ОБЪЯСНЕНИЕ ЯВЛЕНИЯ ПРЕЦЕССИИ
Построим вектор угловой скорости по правилу буравчика:⃗ω
⃗
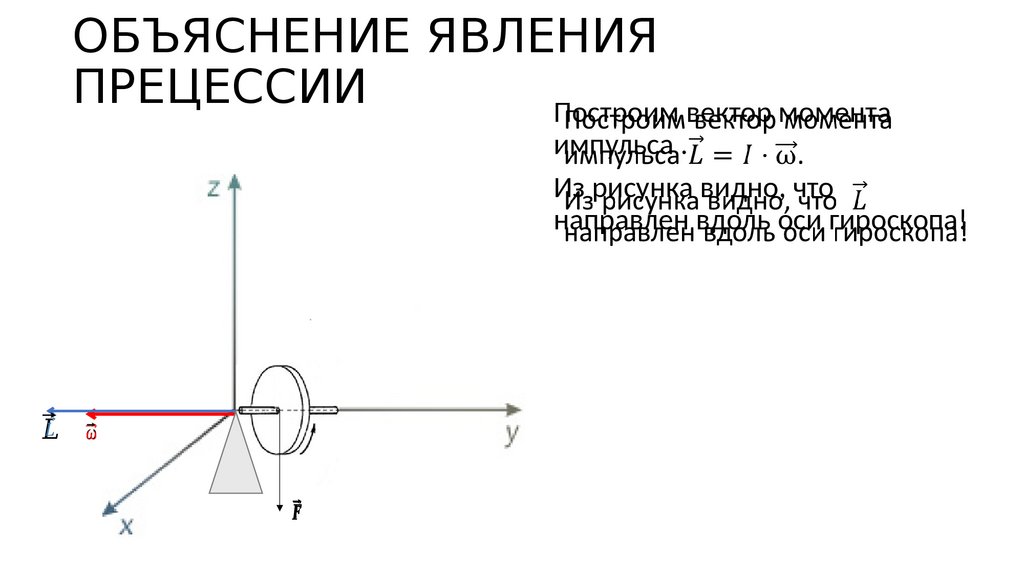
224. ОБЪЯСНЕНИЕ ЯВЛЕНИЯ ПРЕЦЕССИИ
Построим вектор моментаимпульса .
Из рисунка видно, что
направлен вдоль оси гироскопа!
⃗
⃗ω
⃗
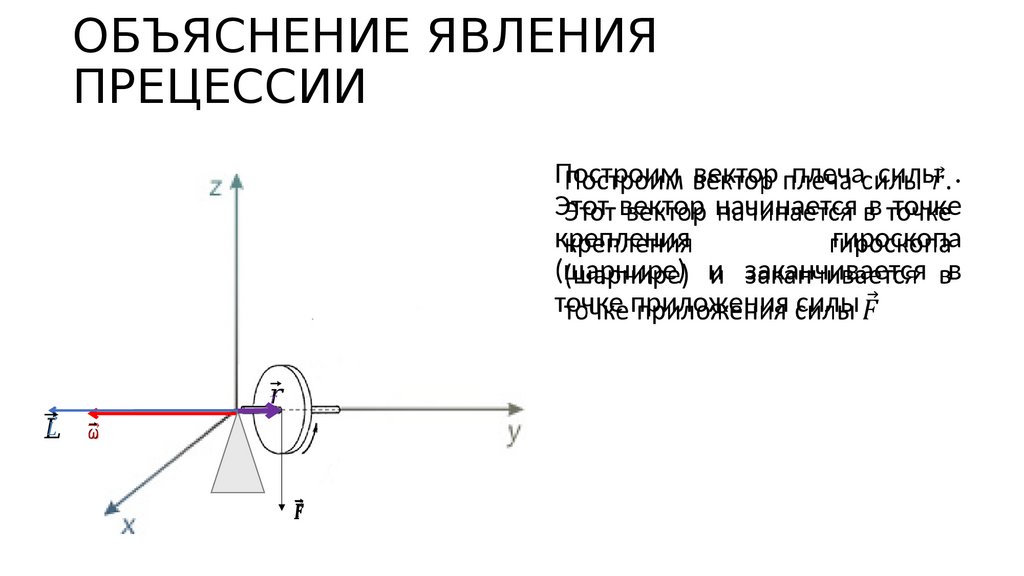
225. ОБЪЯСНЕНИЕ ЯВЛЕНИЯ ПРЕЦЕССИИ
Построим вектор плеча силы .Этот вектор начинается в точке
крепления
гироскопа
(шарнире) и заканчивается в
точке приложения силы
⃗
⃗
⃗ω
⃗
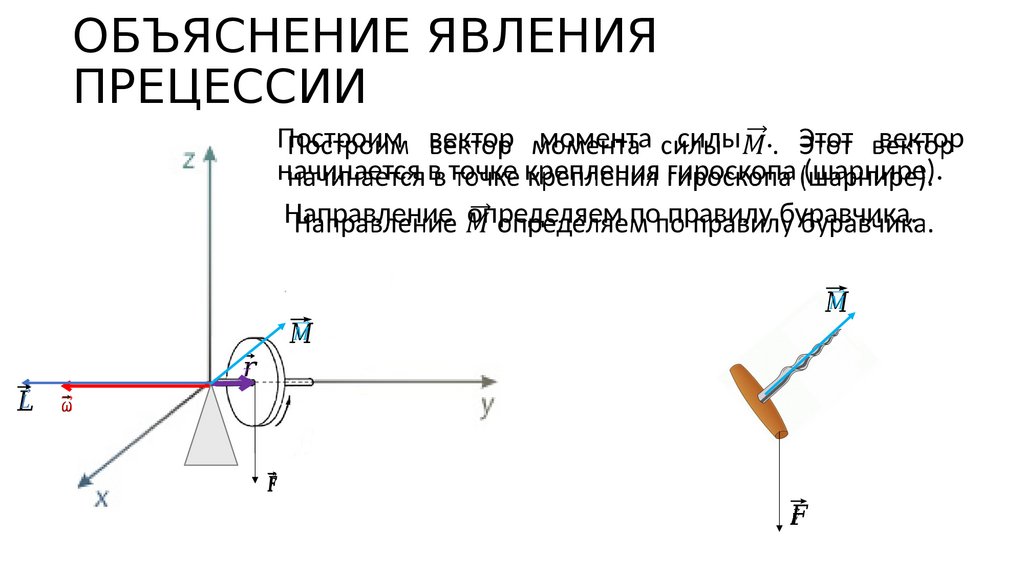
226. ОБЪЯСНЕНИЕ ЯВЛЕНИЯ ПРЕЦЕССИИ
Построим вектор момента силы . Этот векторначинается в точке крепления гироскопа (шарнире).
Направление определяем по правилу буравчика.
⃗
⃗
⃗
⃗
⃗ω
⃗
⃗
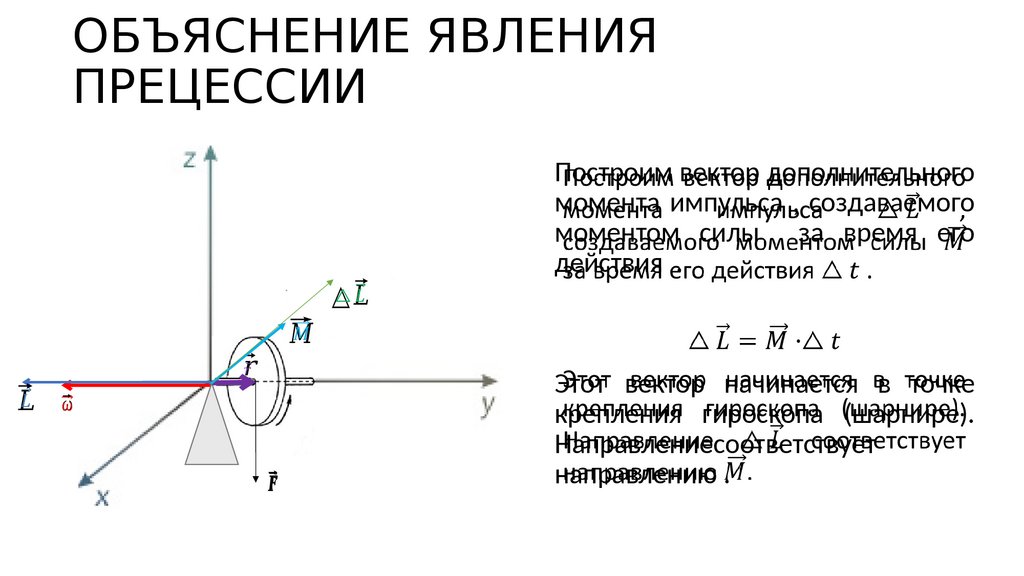
227. ОБЪЯСНЕНИЕ ЯВЛЕНИЯ ПРЕЦЕССИИ
Построим вектор дополнительногомомента импульса , создаваемого
моментом силы за время его
действия .
△⃗
⃗
⃗
⃗
⃗ω
⃗
Этот вектор начинается в точке
крепления гироскопа (шарнире).
Направлениесоответствует
направлению .
228. ОБЪЯСНЕНИЕ ЯВЛЕНИЯ ПРЕЦЕССИИ
⃗′
△⃗
⃗
⃗
⃗
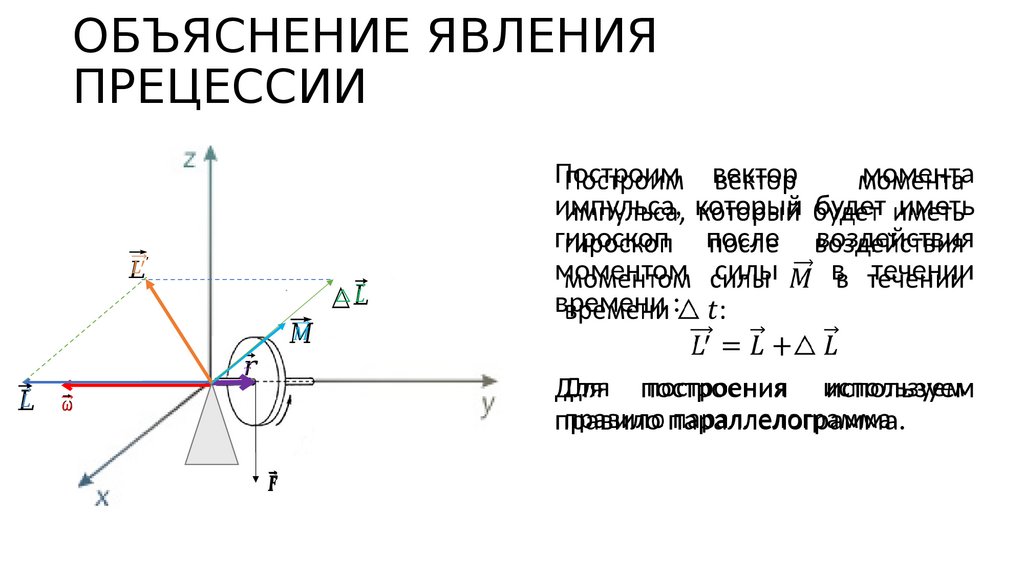
Построим вектор
момента
импульса, который будет иметь
гироскоп после воздействия
моментом силы
в течении
времени :
Для построения используем
правило параллелограмма.
⃗ω
⃗
229.
ОБЪЯСНЕНИЕ ЯВЛЕНИЯПРЕЦЕССИИ
Через промежуток времени ось
гироскопа будет направлена
также как вектор
⃗
′



























































































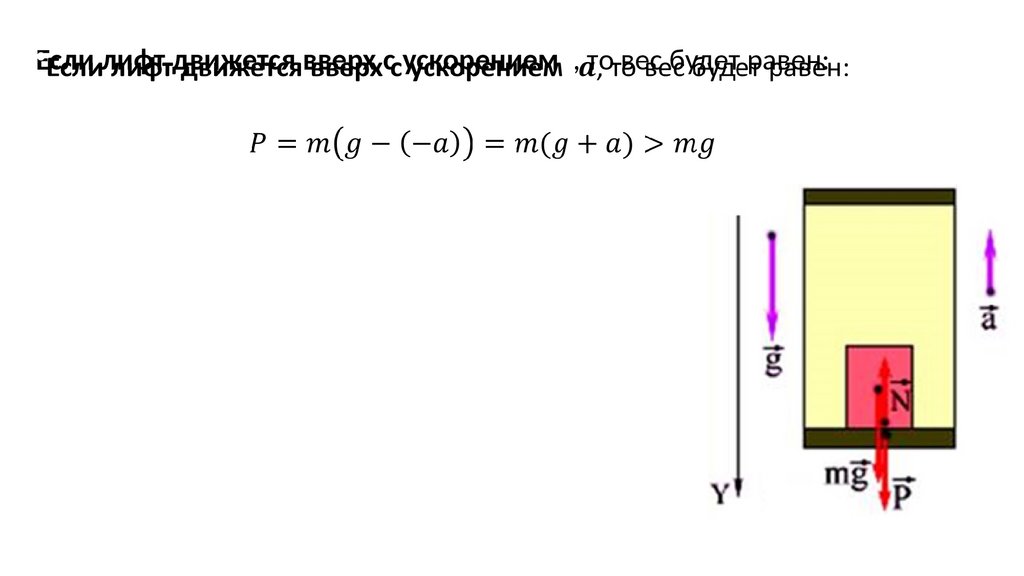







































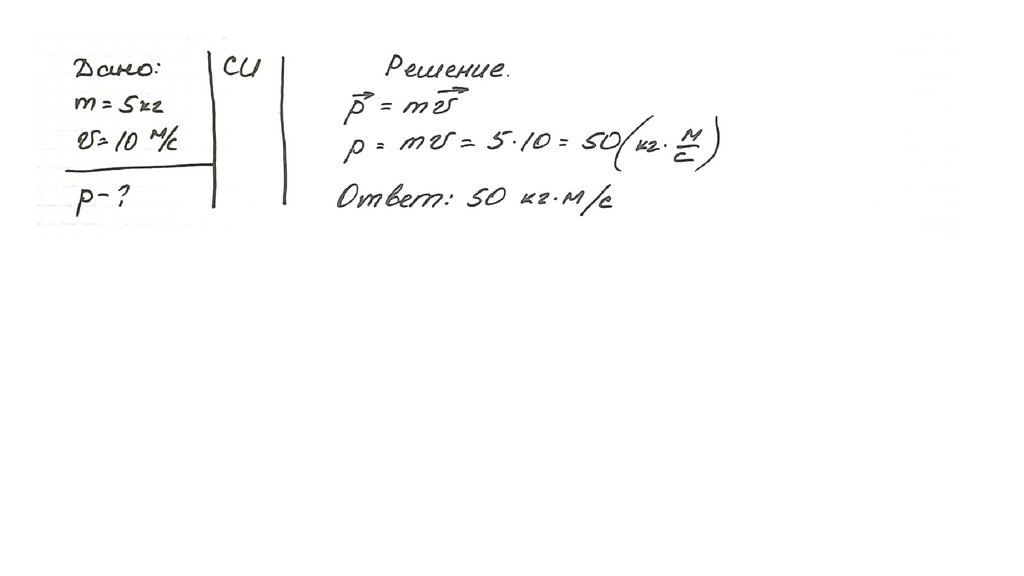




































 Физика
Физика








