Неравенства с одной переменной и их свойства

1. Неравенства с одной переменной и их свойства

Подготовила:
учитель математики
МОУ сош №30 имени А.И.Колдунова
Кутоманова Е.М.
2009-2010 учебный год

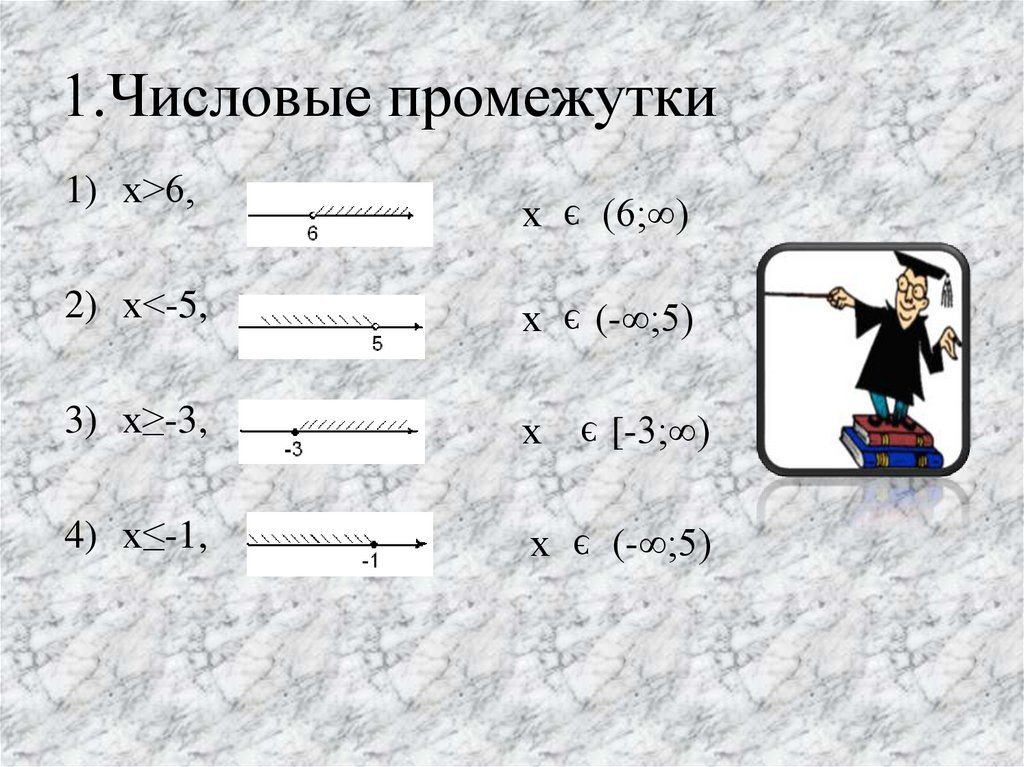
2. 1.Числовые промежутки

1) х>6,
х
э
(6;∞)
2) х<-5,
х
э
(-∞;5)
3) х≥-3,
х
э
[-3;∞)
4) х≤-1,
х
э
(-∞;5)

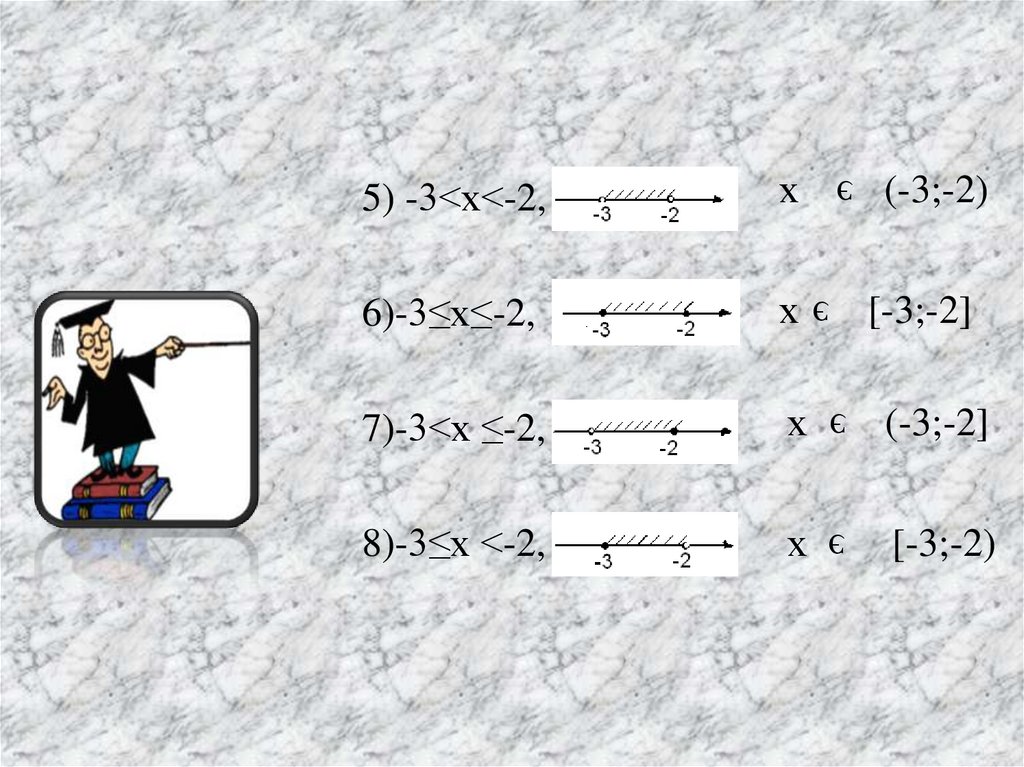
3.

5) -3<х<-2,
х
6)-3≤х≤-2,
х
7)-3<х ≤-2,
х
э
(-3;-2]
8)-3≤х <-2,
х
э
[-3;-2)
(-3;-2)
э
э
[-3;-2]

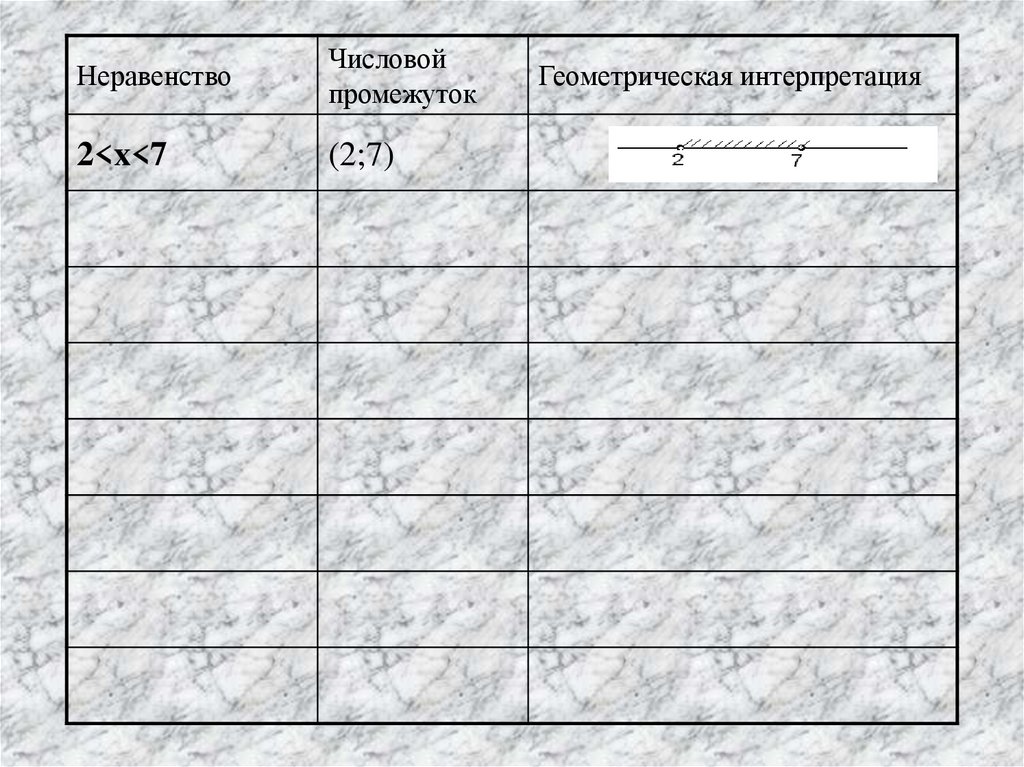
4.

Неравенство
Числовой
промежуток
2<x<7
(2;7)
Геометрическая интерпретация

5.

Неравенство
Числовой
промежуток
2<x<7
(2;7)
-5≤x<-1
[-5;-1)
Геометрическая интерпретация

6.

Неравенство
Числовой
промежуток
2<x<7
(2;7)
-5≤x<-1
[-5;-1)
0,5<x≤1
(-0,5;1]
Геометрическая интерпретация

7.

Неравенство
Числовой
промежуток
2<x<7
(2;7)
-5≤x<-1
[-5;-1)
0,5<x≤1
(-0,5;1]
13≤x≤13,5
[13;13,5]
Геометрическая интерпретация

8.

Неравенство
Числовой
промежуток
2<x<7
(2;7)
-5≤x<-1
[-5;-1)
0,5<x≤1
(-0,5;1]
13≤x≤13,5
[13;13,5]
x>8
(8;+∞)
Геометрическая интерпретация

9.

Неравенство
Числовой
промежуток
2<x<7
(2;7)
-5≤x<-1
[-5;-1)
0,5<x≤1
(-0,5;1]
13≤x≤13,5
[13;13,5]
x>8
(8;+∞)
x<17
(-∞;17)
Геометрическая интерпретация

10.

Неравенство
Числовой
промежуток
2<x<7
(2;7)
-5≤x<-1
[-5;-1)
0,5<x≤1
(-0,5;1]
13≤x≤13,5
[13;13,5]
x>8
(8;+∞)
x<17
(-∞;17)
x≥-15
[-15;+∞)
Геометрическая интерпретация

11.

Неравенство
Числовой
промежуток
2<x<7
(2;7)
-5≤x<-1
[-5;-1)
0,5<x≤1
(-0,5;1]
13≤x≤13,5
[13;13,5]
x>8
(8;+∞)
x<17
(-∞;17)
x≥-15
[-15;+∞)
x≤6
(-∞;6]
Геометрическая интерпретация

12.

Множество действительных чисел
изображается всей координатной
прямой. Его обозначают так: (-∞;∞).
Например:
1)
[1;5]∩[3;7]=[3;5].
2)
[1;5]U[3;7]=[1;7].

13. 2.Решение неравенств с одной переменной.

Определение.
Решением неравенства с одной переменной называется
значение переменной, которое обращает его в верное
равенство.
Например: Рассмотрим неравенство 6х-5>7 .
Подставим вместо х число 1, тогда
получится неравенство 6·1-5>7, которое не
является верным.
Подставим вместо х число 3, тогда
получится верное неравенство 6·3-5>7.
Число 3 является решением неравенства
6х-5>7 или удовлетворяет этому
неравенству.

14. Свойства: 1.Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное

неравенство.
2.Если обе части неравенства умножить или разделить на одно и то же
положительное число, то получится равносильное неравенство.
Если обе части неравенства умножить или разделить на одно и то же
отрицательное число, изменив при этом знак неравенства на противоположный,
то получится равносильное неравенство.
2) 10х+20<5х,
10х-5х<-20,
5х<-20,
х<-4.
-5
х
э
Например:
1) 15+3х>0,
3х>-15,
х>-5.
х (-5;∞)
(-∞; -4)
-4
э

15. Решим задачу:

Длина стороны стороны прямоугольника 8 см. Какой должна
быть длина другой стороны, чтобы периметр
прямоугольника был меньше периметра квадрата со
стороной 10 см?
Пусть х см длина другой стороны
прямоугольника (х>0), тогда его периметр Р
равен 2(х+8) см.
Периметр квадрата со стороной 10 см
равен 40 см.
Имеем: 2(х+8)<40,
х+8<20,
х<12.
Учитывая, что х>0, имеем 0<х<12.

16. Рассмотрим ещё один пример: При каких значениях переменной выражение √ 5х-15 имеет смысл?

5х-15≥0,
5х≥15,
х≥5.
Выражение √5х-15 имеет
смысл при х≥5.