Задание на исследование функции с помощью производной

1.

ЕГЭ 2014
Задания В 15
1

2.

Тип задания: Задание на исследование функции с
помощью производной
Характеристика задания: Задание на вычисление с
помощью производной экстремума данной функции
или наибольшего (наименьшего) значения данной
функции на заданном отрезке
Комментарий: Решение задачи связано с
нахождением при помощи производной точек
максимума (минимума) заданной функции или ее
наибольшего (наименьшего) значения на отрезке.
Если функция задана формулой, то при нахождении
наибольшего (наименьшего) значения функции на
отрезке можно использовать стандартный алгоритм
2

3. Таблица производных

Функция
Производная
Функция
Производная
С (с – const)
0
sinx
cosx
xn
nxn-1
cosx
- sinx
lnx
1/x
tgx
1/cos2x
ax
ax ·lna
ctgx
-1/sin2x
ex
ex
logax
1/x·lna
3

4. Правила вычисления производных

(f(x)+g(x))´=f´(x)+g´(x)
(f(x)-g(x))´=f´(x)-g´(x)
(f(x)·g(x))´=f´(x)·g(x)+f(x)·g´(x)
(f(x)/g(x))´=(f´(x)·g(x)f(x)·g´(x))/g2(x)
(f(g(x))´=f´(g(x))·g´(x)
4

5. Алгоритм отыскания наибольшего (наименьшего) значения функции на заданном отрезке

1.
2.
3.
4.
5.
Найти производную функции
Найти значения х, при которых производная
равна нулю
Выбрать из значений х, найденных в п.2 те,
которые принадлежат заданному отрезку
Вычислить значения функции на концах
заданного отрезка и в точках, определенных
в п.3
Выбрать наибольшее (наименьшее) значение
функции
5

6.

1. Найти наименьшее значение функции
на отрезке [-9; -7]
Решение
Ответ: 0
6

7.

2. Найти наименьшее значение функции
на отрезке [0; π/2]
Решение
Ответ: -15
7

8.

3. Найти наибольшее значение функции
на отрезке [0; π/2]
Решение
Ответ: 3
8

9.

4. Найти наибольшее значение функции
на отрезке [-4; -1]
Решение
Ответ: -6
9

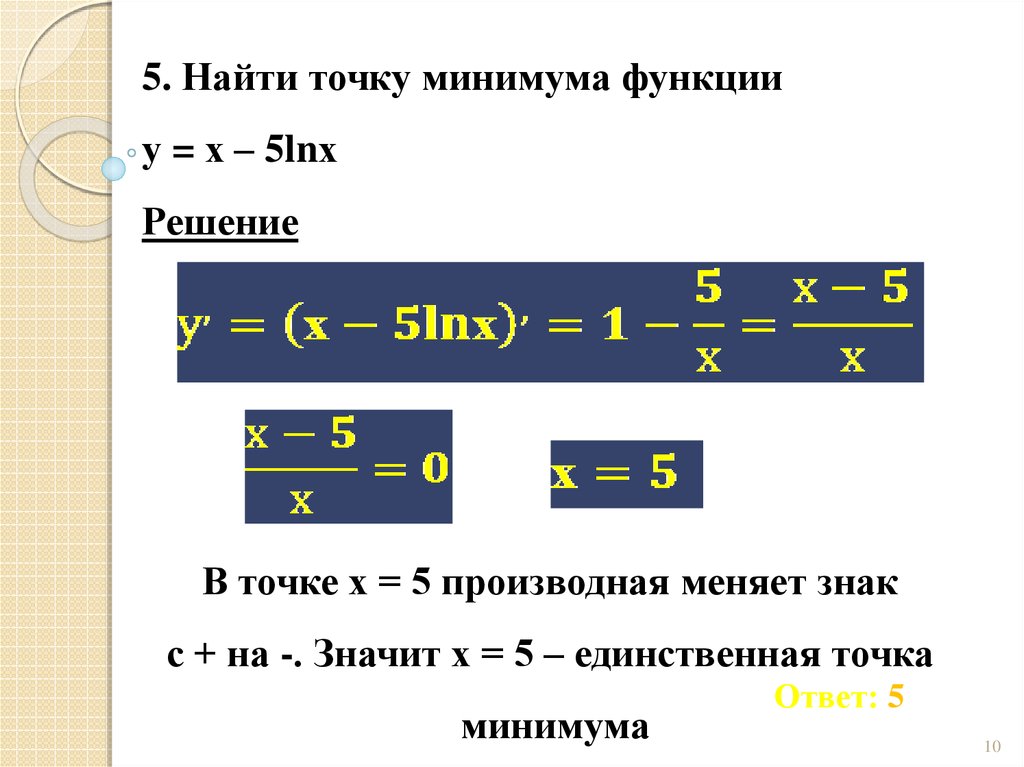
10.

5. Найти точку минимума функции
у = х – 5lnх
Решение
В точке х = 5 производная меняет знак
с + на -. Значит х = 5 – единственная точка
минимума
Ответ: 5
10

11.

6. Найти наибольшее значение функции
у = 5 – 7х + 7ln(х + 3) на отрезке [-2,5; 0]
Решение
Ответ: 19
11