Похожие презентации:
Решение задач практического содержания
1. РЕШЕНИЕ ЗАДАЧ ПРАКТИЧЕСКОГО СОДЕРЖАНИЯ
2.
Задача для буржуяB10 (№ 6081) Для одного из предприятиймонополистов зависимость объёма
спроса на продукцию q (единиц в месяц)
от её цены p (тыс. руб.) задаётся
формулой: q 150 15 p . Определите
максимальный уровень цены p (в тыс.
руб.), при котором значение выручки
предприятия за месяц r q p
составит не менее 360 тыс. руб.
3. Решение задач практического содержания
Обратите внимание на единицу измерения Р (в тыс.рублях), тогда 360000 это 360 (в тысячах рублей)
В равенство, выражающее значение выручки за
месяц
r q p подставим
q 150 15 p
Получаем выручку за месяц:
r (150 15 p) p
r 150 p 15 p 2
4. Решение задач практического содержания
По условию выручка должна быть неменее (т.е. больше или равна)
360 тыс.рублей
150 p 15 p 360 : 15
2
p 10 p 24 0
2
5. Решение задач практического содержания
p 4(тыс. руб )p 6(тыс. руб )
4 p 6
Учитывая условие – определить максимальный уровень
цены – получаем
Р = 6000 рублей
6. Решение задач практического содержания
Задача для прапорщикаB10 (№ 6089) Модель камнеметательной машины
выстреливает камни под определенным углом к
горизонту с фиксированной начальной скоростью. Её
конструкция такова, что траектория полета камня
2
y
ax
bx,
описывается формулой ,
1
где a
12000
1
b
15
1/м, — постоянные параметры. На каком наибольшем
расстоянии (в метрах) от крепостной стены высоты
10 м нужно расположить машину, чтобы камни
перелетали через неё?
7. Решение задач практического содержания
11
2
y
x x
12000
15
Высота стены 10 м, поэтому
1
1
2
x x
12000
15
10
x 2 800 x 120000 0
( 12000)
8. Решение задач практического содержания
200 x 600Наибольшее расстояние 600 м
9. Решение задач практического содержания
Задача для Юрия ДмитриевичаB10 (№ 6115) Зависимость температуры (в градусах
Кельвина) от времени (в минутах) для
нагревательного элемента некоторого прибора была
получена экспериментально и на исследуемом
интервале температур задаётся выражением
T (t ) To at bt 2 , где To 1160 K , a 34 K / мин, b 0,2 K / 2 .
Известно, что при температурах нагревателя свыше
2000 К прибор может испортиться, поэтому его нужно
отключать. Определите (в минутах) через какое
наибольшее время после начала работы нужно
отключать прибор.
10. Решение задач практического содержания
После подстановки параметровполучим:
T (t ) 1160 34t 0,2t
Отключение проводится при
2
t 2000K
Решим неравенство:
1160 34t 0,2t 2000
2
( 0,2)
11. Решение задач практического содержания
t 170t 4200 02
30 t 140
Прибор отключится через 30 мин.
12. Решение задач практического содержания
Соблюдайте электробезопасность!B10 (№ 6147) В розетку электросети подключены
приборы, общее сопротивление которых составляет
100Ом. Параллельно с ними в розетку
предполагается подключить электрообогреватель.
Определите (в омах) наименьшее возможное
сопротивление электрообогревателя, если известно,
что при параллельном соединении двух проводников
с сопротивлениями
их общее
R1 и R2
сопротивление даётся формулой
R1 R2
R
,
R1 R2
а для нормального функционирования электросети
общее сопротивление в ней должно быть не меньше
20 Ом.
13. Решение задач практического содержания
Так как R1 100 ом, то100 R2
R
100 R2
– общее сопротивление
Общее сопротивление должно быть не менее
200 ом
100 R2
20
100 R2
14. Решение задач практического содержания
100 R2 2000 20 R280 R2 2000
R2 25
Ответ: R = 25 ом
15. Решение задач практического содержания
МОЯ ЛЮБИМАЯ ЗАДАЧА!!!B10 (№ 6175) Для определения эффективной
температуры звёзд используют закон Стефана —
Больцмана, согласно которому мощность излучения
нагретого тела прямо пропорциональна площади его
поверхности и четвёртой степени температуры:
числовой
P ST 4 , где 5,7 10 8
коэффициент, площадь измеряется в квадратных
метрах, температура — в градусах Кельвина, а
мощность — в ваттах. Известно, что некоторая
1
звезда имеет площадь
16
S
16
10
2
,
17
46
,
17
10
,
а излучаемая ею мощность P не менее
определите наименьшую возможную температуру
этой звезды.
16. Решение задач практического содержания
После подстановки параметров получаемзависимость
1
8
16
P 5,7 10 10
16
Излучаемая мощность должна быть не
17
46,17 10
менее
поэтому
необходимо решить неравенство
1
16
4
17
5,7 10 10 T 46,17 10
16
8
17. Решение задач практического содержания
.46,17 10 16
T
8
5,7 10
46,17 10 16
T
8
5,7 10
T 8,1 10 1
T 8,1 10 16
17
4
4
9
T 81 10 16
4
T 1200
17
4
4
9
8
Итак, наименьшая
возможная температура
звезды 1200К
18.
.19. Найти значение выражений
20.
1log 3 9 2
2
log 3 1 0
3
4
1
log 3
3
27
1
1
log 3
2
3
21.
56
7
8
log 3
3
2
9
3
log 3 3
3
3
1
log 2
3
0,125
1
2
3
lg( 0,1 100 ) lg( 10 10 ) lg 10
3
1
3
1
3
22.
23.
9log 1 5
5
5
10
11
6 4,5
1,5
log4 , 5 9
log1, 5 6
1
5
54
3 3
24.
1213
14
15
2
log2 4
2
log2 32
32
lg100
100
10
5
4
log5 3
3
16
17
18
19
3
1
2
2
1
3
log3 3
log 1 1
2
log2 5 2
25
log5 3
1
25
9
25.
26.
2021
22
23
4
log2 3
27
3
5
log3 2
9
2 log3 10
2 log5 10
8
90
2,5
24
25
26
27
8
2 log8 5
1 24
1
2
9 3
1
4
16
1
2
2
121 11
27.
2829
30
31
1
3
27 3
1
6
64 2
2
3
8 4
4
3
8 16
32
33
34
35
3
4
81 27
1
2
0,01
2
3
2
2
10
1
2
16 1
1
4
1
81
3



















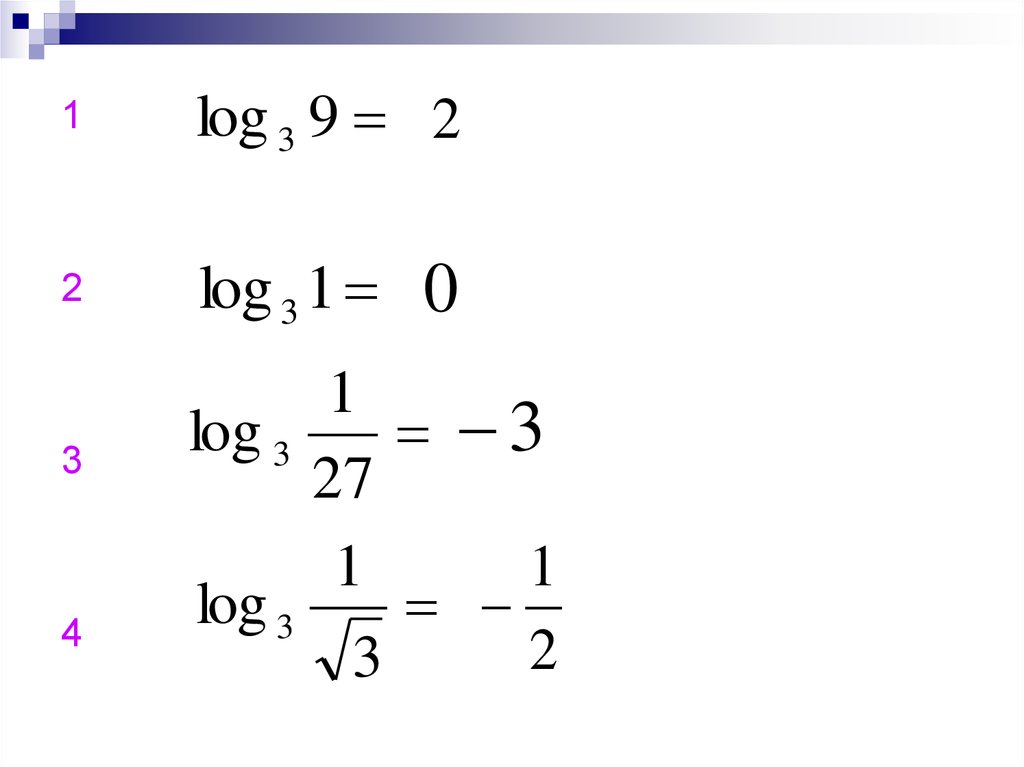
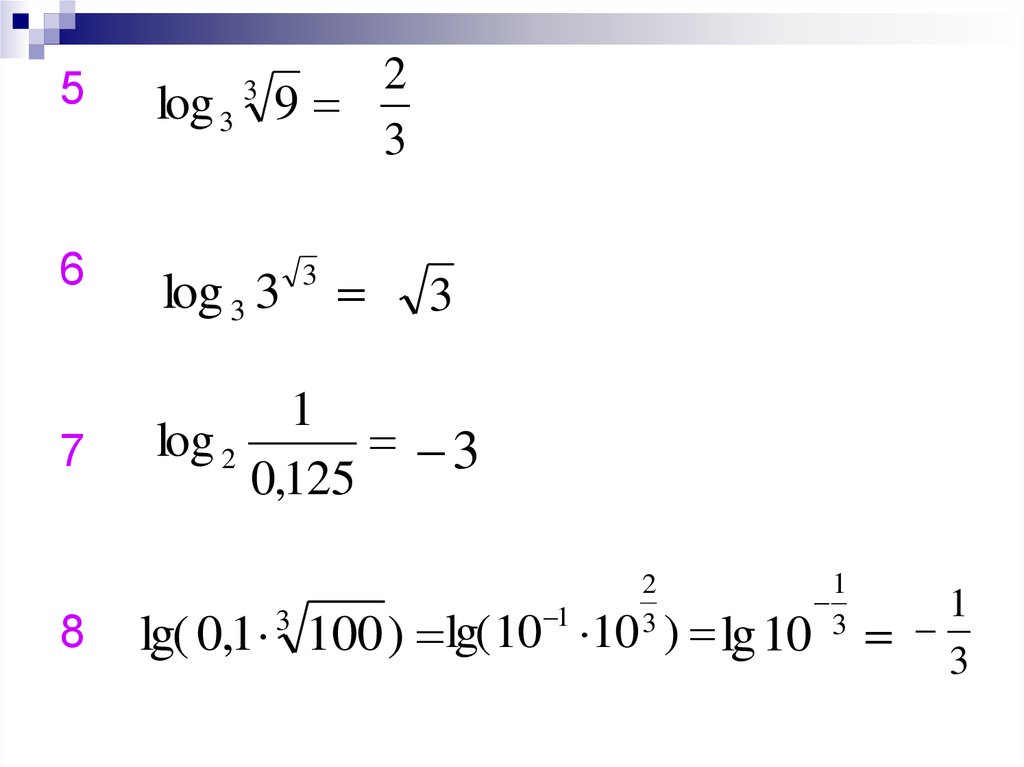

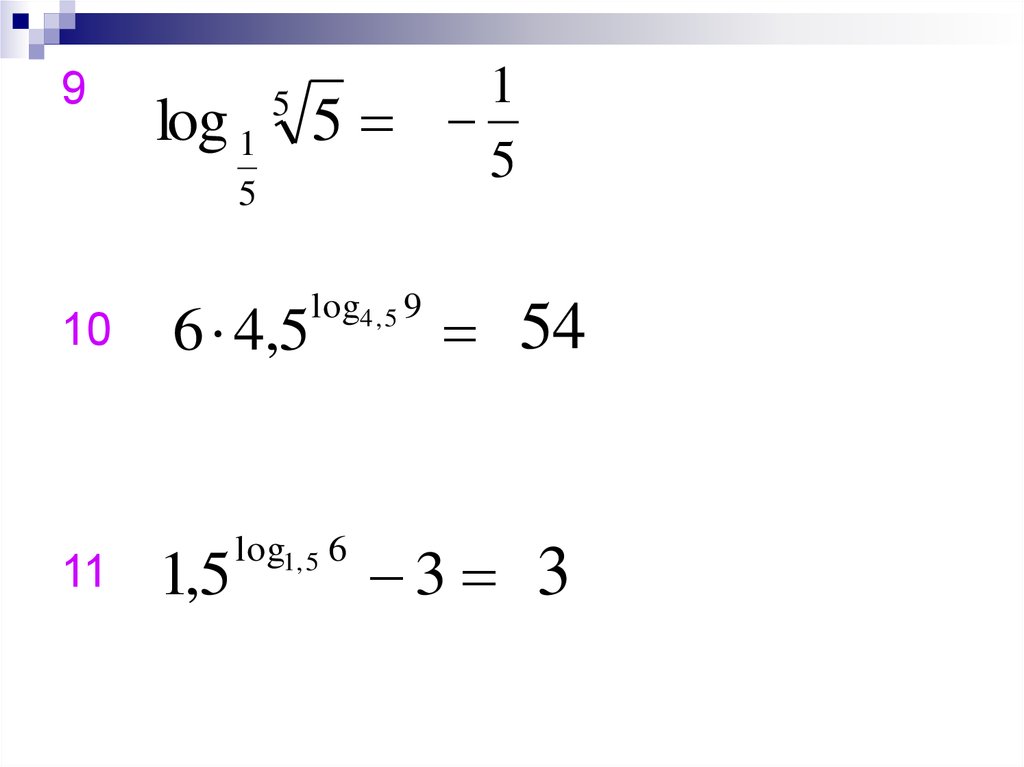
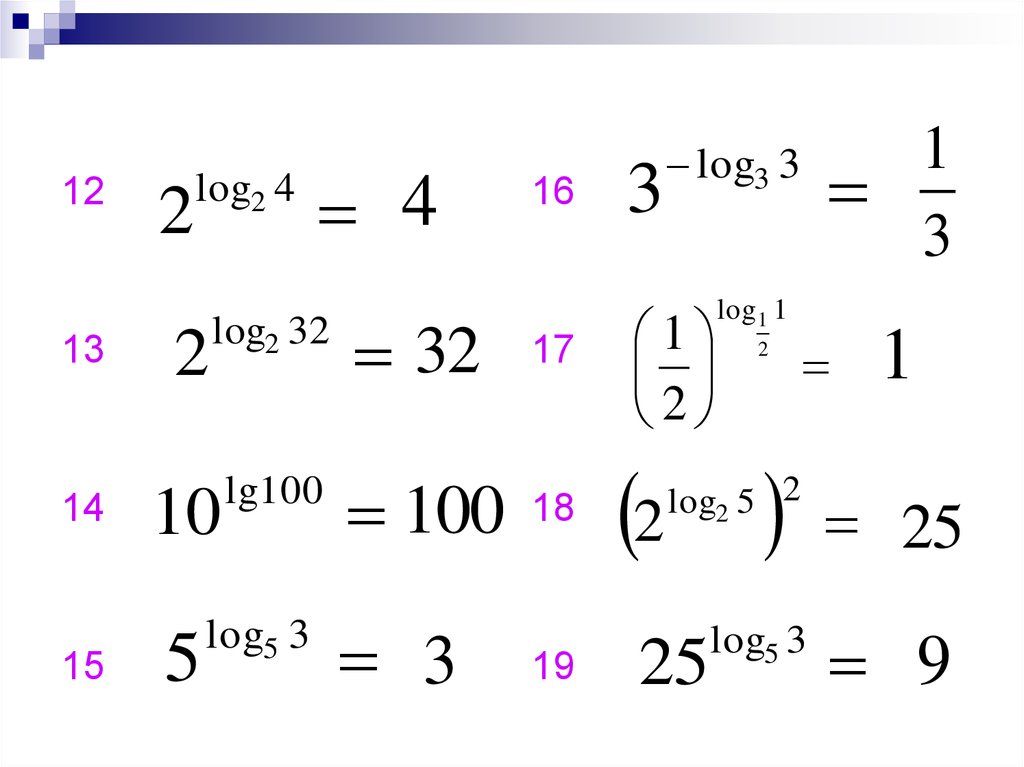




 Математика
Математика