Линейная функция и ее график. 7 класс

1. Линейная функция и ее график 7класс

АЛГЕБРА

2. Маршрут урока

1 станция «Теоретическая разминка»
2 станция «Построение графика линейной функции»
3 станция «Нахождение значения функции»
4 станция «Нахождение значения аргумента»
5 станция «Нахождение координат точки пересечения
графиков функций»
станция Физкультминутка
6 Станция «Практическое применение линейной
функции и её графика»
7 станция «Параметры»
8 Итоговое тестирование
Подведение итогов
1 Домашнее задание

3. 1 станция «Теоретическая разминка»

• Какую зависимость одной переменной от
другой называют функциональной?
• Какая переменная называется функцией?
• Какая переменная называется
аргументом?
• Назовите способы задания функции.
• Что называется линейной функцией?

4. Линейная функция

Функция , которую можно задать
формулой вида y = kx + b,
где x – независимая переменная, k,
b - некоторые числа

5.

• Как называется частный случай линейной
функции y=kx+b при b=0, k 0?

6. Какие из функций являются прямой пропорциональностью.

Какие из функций являются прямой
пропорциональностью.
• 1 вариант
2 вариант
а) y=17x
а) y=-5x
x
б) y=
13
в) y = 13
х
б) y=
9х
2
7x
в) y =
9

7. Какие из функций являются линейными?

a) y=2x-3
линейная функция,
k=2
б)y=7-9x =-9x+7 линейная функция, k=-9
x
1
1
в ) y 1 x 1 линейная функция, k
2
2
2

8.

2
г ) y 1 функция нелин. т.к. x в знаменателе
x
д) y x 3 функция нелин. т.к. x в квадрате
10 x 7 10 x 7
2
е) y
2x 1
5
5
5
5
2
линейная функция,
k=2

9.

• Что является графиком линейной
функции?
• Назовите угловой коэффициент линейной
функции y=kx+b.
• Что показывает угловой коэффициент
линейной функции y=kx+b?
• Что показывает b?

10.

• По схематическому графику линейной
функции, укажите какие знаки принимают
kиb

11.

b
k
y
y
0
x
y
0
x
x
0
x
y
y
y
0
0
x
x
0
x
y
y
y
0
0
x
x
0
x
x

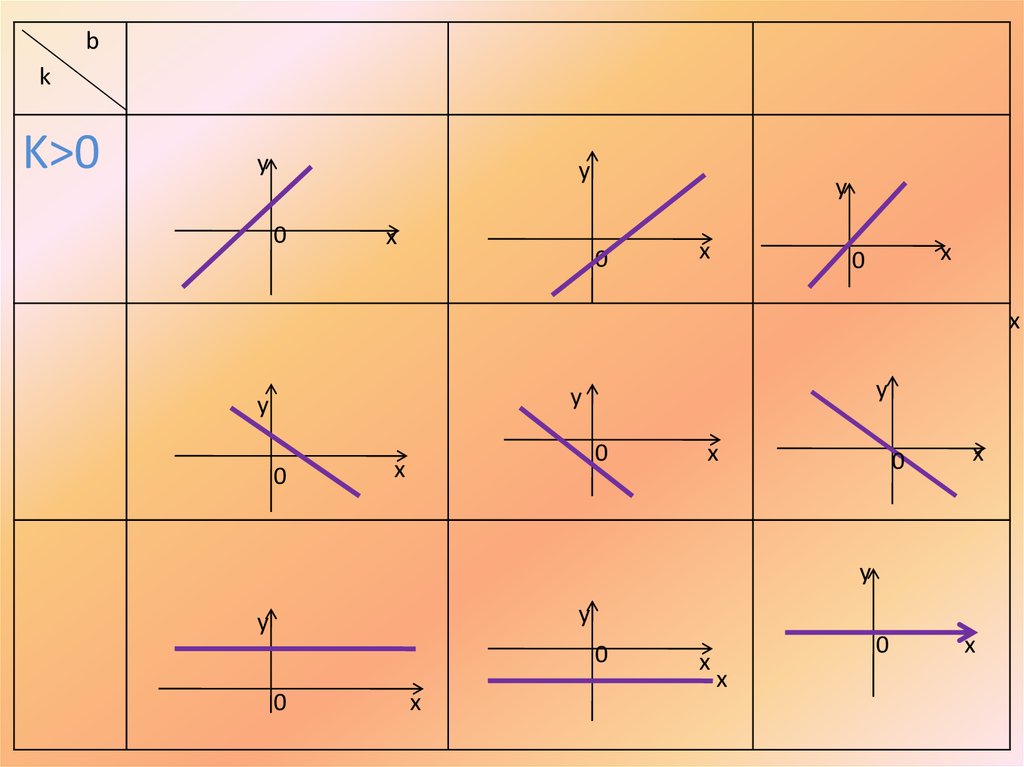
12.

b
k
K>0
y
y
0
x
y
0
x
x
0
x
y
y
y
0
0
x
x
0
x
y
y
y
0
0
x
x
0
x
x

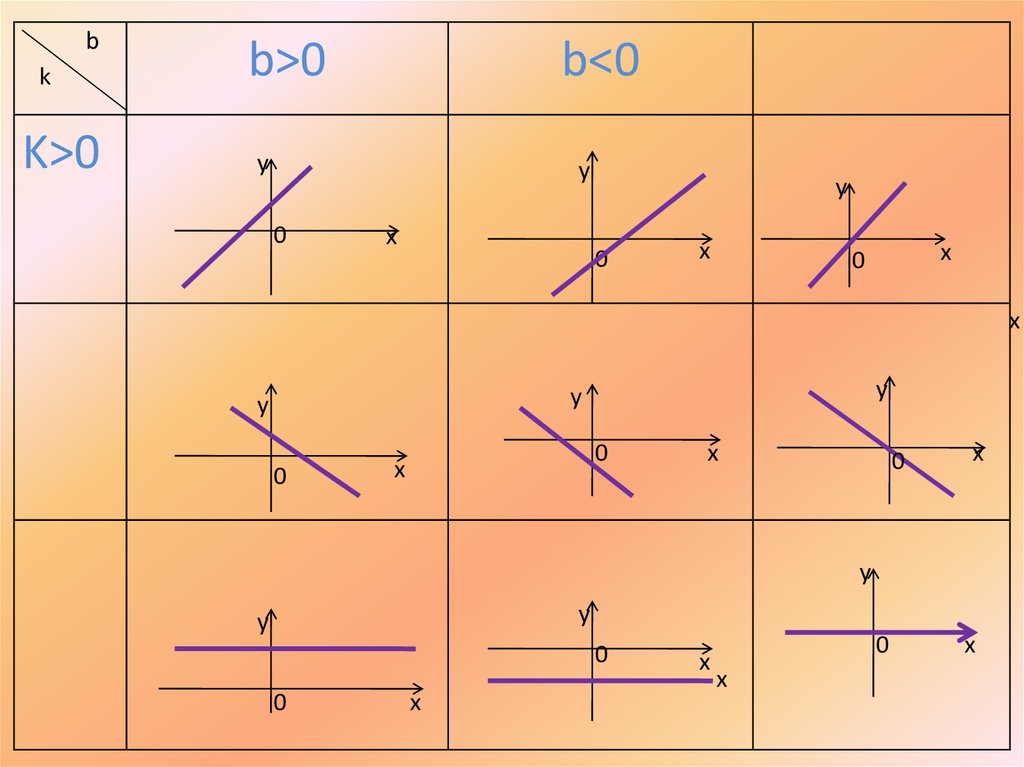
13.

b
k
K>0
b>0
y
y
0
x
y
0
x
x
0
x
y
y
y
0
0
x
x
0
x
y
y
y
0
0
x
x
0
x
x

14.

b
k
K>0
b>0
b<0
y
y
0
x
y
0
x
x
0
x
y
y
y
0
0
x
x
0
x
y
y
y
0
0
x
x
0
x
x

15.

b
k
K>0
b>0
b<0
y
b=0
y
0
x
y
0
x
x
0
x
y
y
y
0
0
x
x
0
x
y
y
y
0
0
x
x
0
x
x

16.

b
k
K>0
b>0
b<0
y
b=0
y
0
x
y
0
x
x
0
x
K<0
y
y
y
0
0
x
x
0
x
y
y
y
0
0
x
x
0
x
x

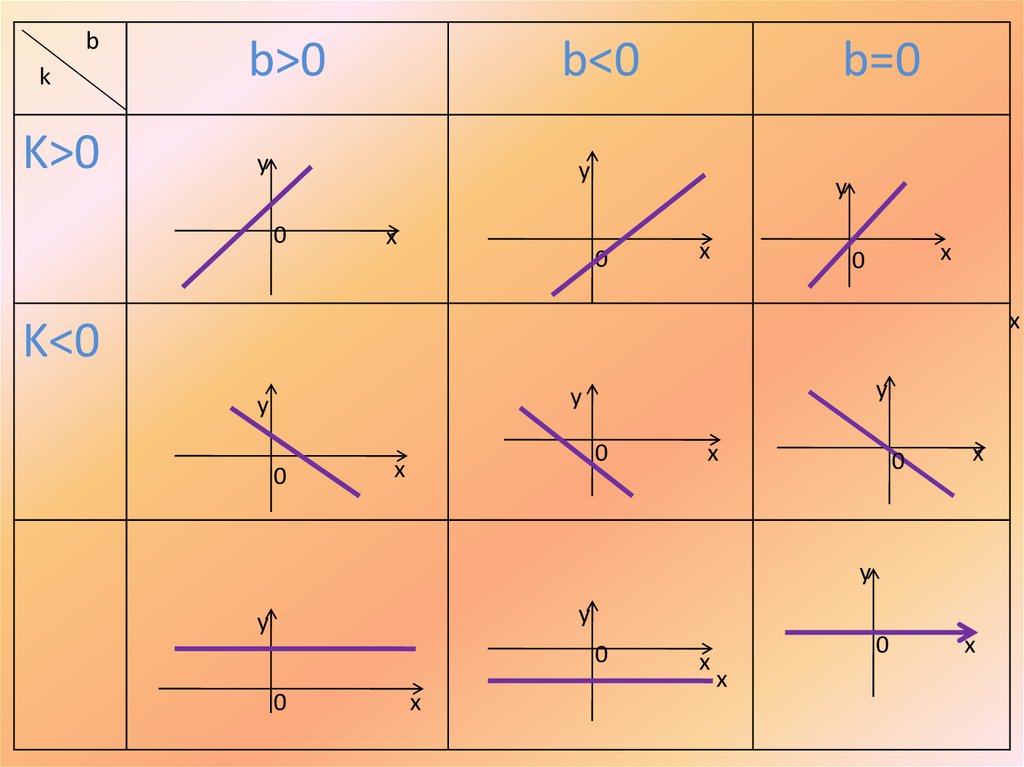
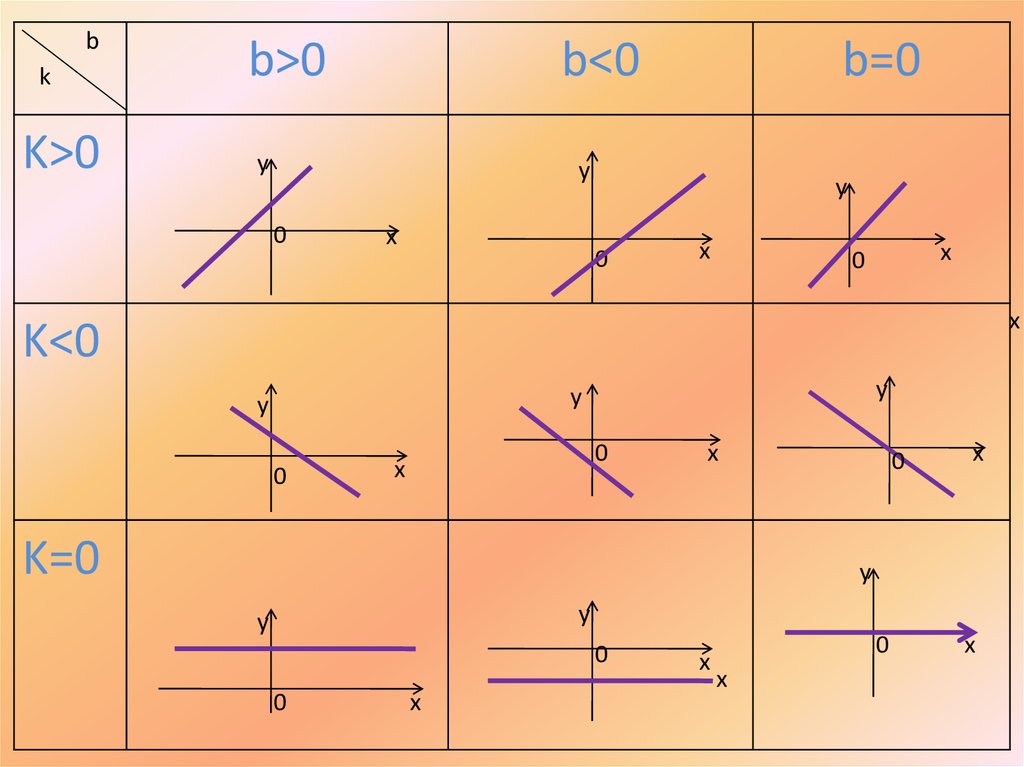
17.

b
k
K>0
b>0
b<0
y
b=0
y
0
x
y
0
x
x
0
x
K<0
y
y
y
0
0
x
x
K=0
0
x
y
y
y
0
0
x
x
0
x
x

18.

• При каком условии прямые,
заданные формулами
y k1 x b1
и
y k2 x b2
параллельны?

19.

• При каком условии прямые,
заданные формулами
y k1 x b1
и
y k2 x b2
параллельны?
k1 k2
и b1 b2

20.

• При каком условии прямые,
заданные формулами
y k1 x b1
и
y k2 x b2
пересекаются?

21.

• При каком условии прямые,
заданные формулами
y k1 x b1
и
y k2 x b2
пересекаются?
k1 k2

22.

• Как звали ученого, создавшего
координатную сетку на плоскости по
аналогии с географическими
координатами?

23. Французский ученый Оресм, 14 век

24.

• Кто из ученых впервые создал
прямоугольную систему координат?

25. Французский ученый Рене Декарт, 17 век

26. 2 станция «Построение графика линейной функции»

Постройте в одной системе координат
графики функций
y 0,5 x 3 и
1
y x
4

27. 3 станция «Нахождение значения аргумента по заданному значению функции »

Найдите какое значение принимает
функция
y 0,5 x 3
при x=8

28. 3 станция «Нахождение значения аргумента по заданному значению функции »

Какое значение принимает функция
y 0,5 x 3
при x=8 ?
y (8) 0,5 8 3 1
A(8;1)

29. 4 станция «Нахождение значения аргумента по заданному значению функции »

При каком значении аргумента, значение
функции
1
y x
4
равно -1,5

30. 4 станция «Нахождение значения аргумента по заданному значению функции »

Найдите при каком значении аргумента
значение функции
1
y x
4
равно -1,5
y 1,5,
1
если x 1,5
4
x 6
(6; 1,5)

31. 5 станция «Нахождение координат точки пересечения графиков функций»

Найдите координаты точки пересечения
графиков функции
1
y 0,5 x 3 и y x
4

32. 5 станция «Нахождение координат точки пересечения графиков функций»

Найдите координаты точки пересечения
графиков функции
1
y 0,5 x 3 и y x
4
1
x 0,5 x 3
4
x 4
y (4) 1
Ответ : (4;1)

33. 6 станция «Физкультминутка»

34. 6 станция «Практическое применение линейной функции и её графика»

Скорость распространения звука в воздухе в
зависимости от температуры воздуха может
быть найдена приближенно по формуле
v 331 0, 6t ,
где v скорость ( м / с ), t температура ( С ).
Найдите скорость распространения звука в
зимний день с температурой 35 С
и в летний день с температурой 35 С.

35. 6 станция «Практическое применение линейной функции и её графика»

Скорость распространения звука в воздухе в
зависимости от температуры воздуха может
быть найдена приближенно по формуле
v 331 0, 6t ,
где v скорость ( м / с ), t температура ( С ).
Найдите скорость распространения звука в
зимний день с температурой 35 С
и в летний день с температурой 35 С.
Ответ:
310 м / с, 541 м / с.

36. В медицине и сейсмологии

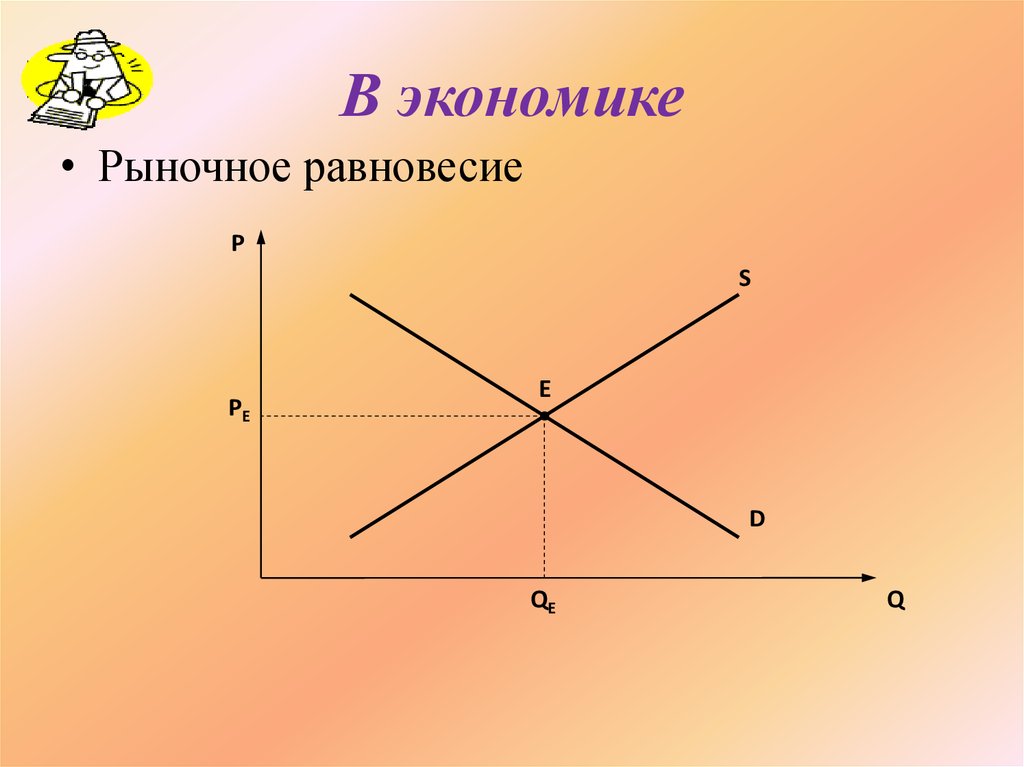
37. В экономике

• Рыночное равновесие
P
S
PE
E
D
QE
Q

38. В физике

Путь метеорита на звездном небе
След альфа-частиц в камере Вильсона

39. 7 станция «Параметры»

1. Найдите значение a, если известно, что
график функции y ax 4 проходит через
точку М(3;-2).
2. График линейной функции параллелен
графику функции y 5 x 0,7 и проходит
через точку А(-1,2; -6). Найдите формулу
линейной функции.

40. 2.

1. 3a 4 2
2.
y kx b
3a 6
k 5
a 2
y 5x b
Ответ : a 2
5 ( 1, 2) b 6
b 0
Ответ : y 5 x.

41. 8 станция «Итоговое тестирование»

42. Домашнее задание

№ 365, 370, 372(а,б)
Температура воздуха в Чебоксарах с 0 часов
до 10 часов 18 ноября изменялась линейно.
Узнайте температуру воздуха с 0 часов до 10
часов 18 ноября и найдите формулу
линейной функции (x-время в часах с шагом
1; y-температура воздуха). Постройте график
изменения температуры воздуха в данном
периоде времени.
Какая температура
воздуха была в нашем городе в 8 часов?

43. Итоги урока: