Применение производной при исследовании функций

1. Применение производной при исследовании функций

2. Доказать, что функция монотонна на заданном промежутке:

y 4 x 2008; если х ;
у 2 х sin x; если х ;
y x x 448; если х .
5
3

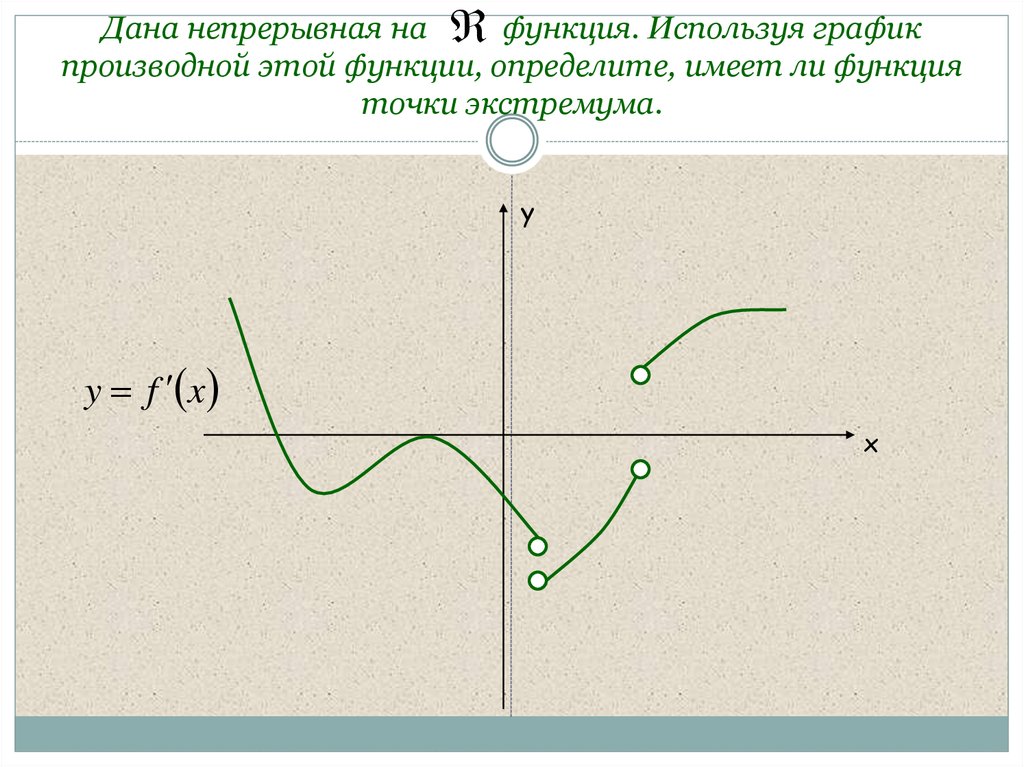
3. Дана непрерывная на функция. Используя график производной этой функции, определите, имеет ли функция точки экстремума.

y
y f x
x

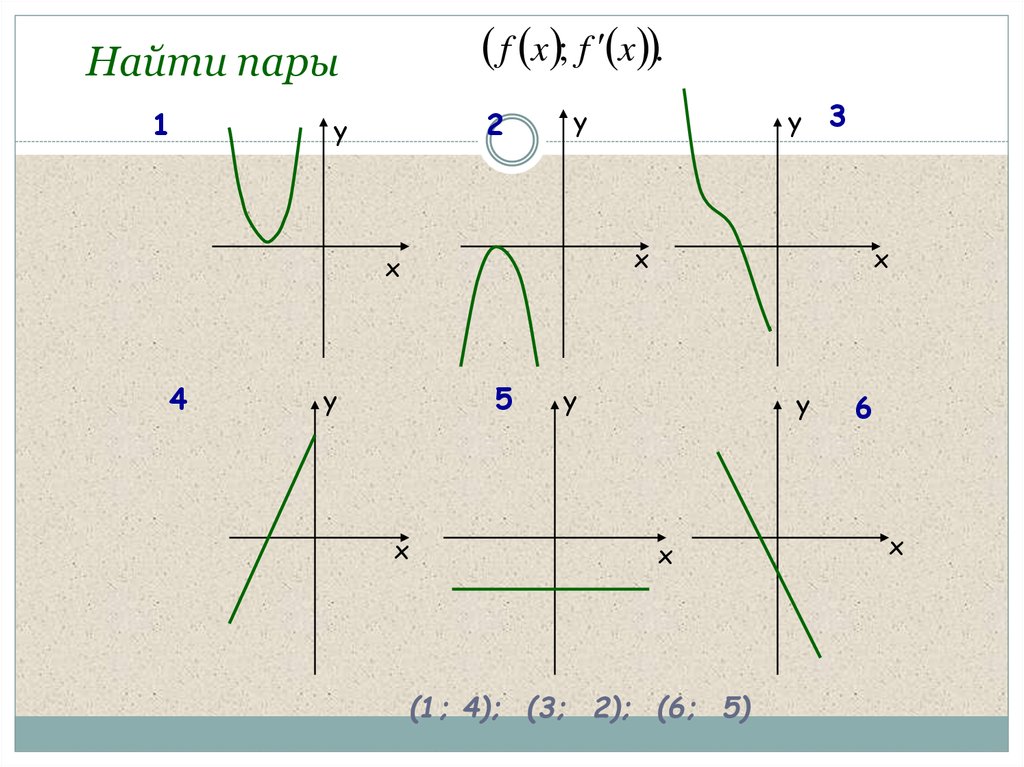
4. Найти пары

f x ; f x .
Найти пары
1
2
y
y
5
y
x
3
x
x
4
y
x
y
y
x
(1; 4); (3; 2); (6; 5)
6
x

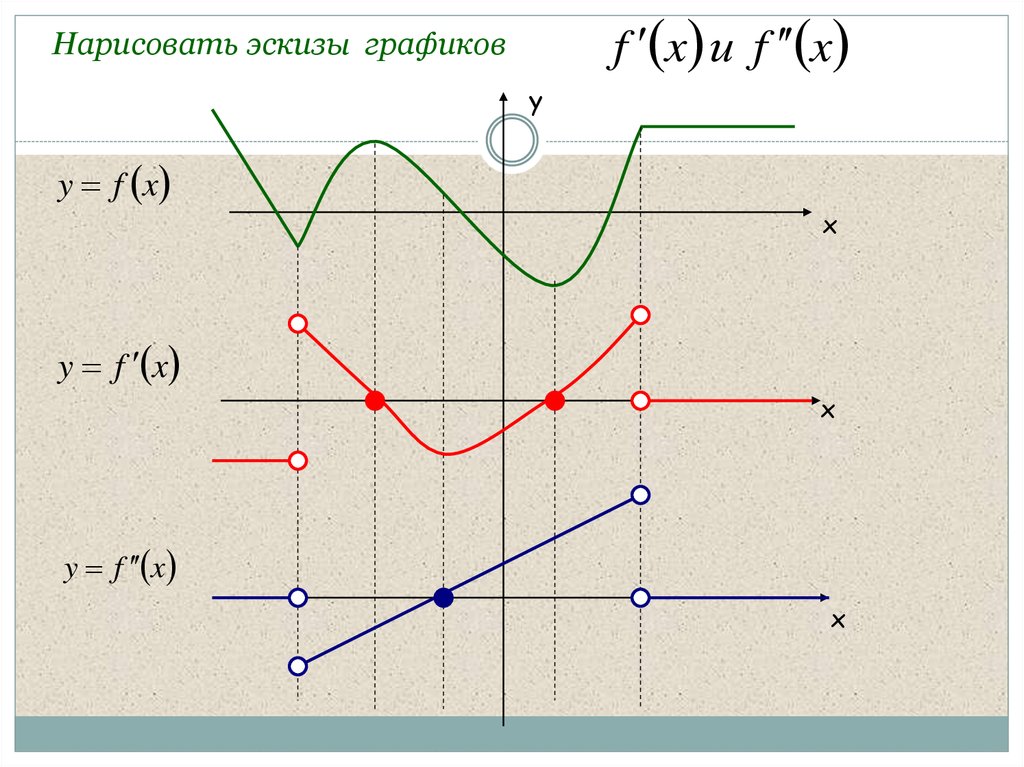
5. Нарисовать эскизы графиков

f x и f x
Нарисовать эскизы графиков
y
y f x
x
y f x
x
y f x
x

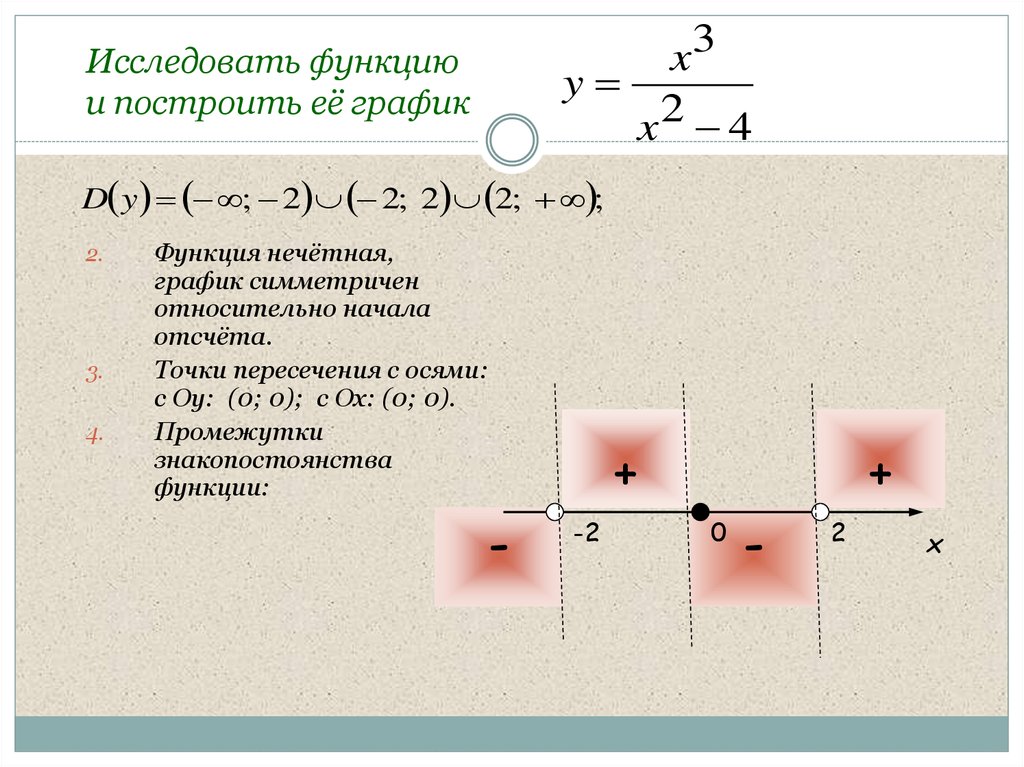
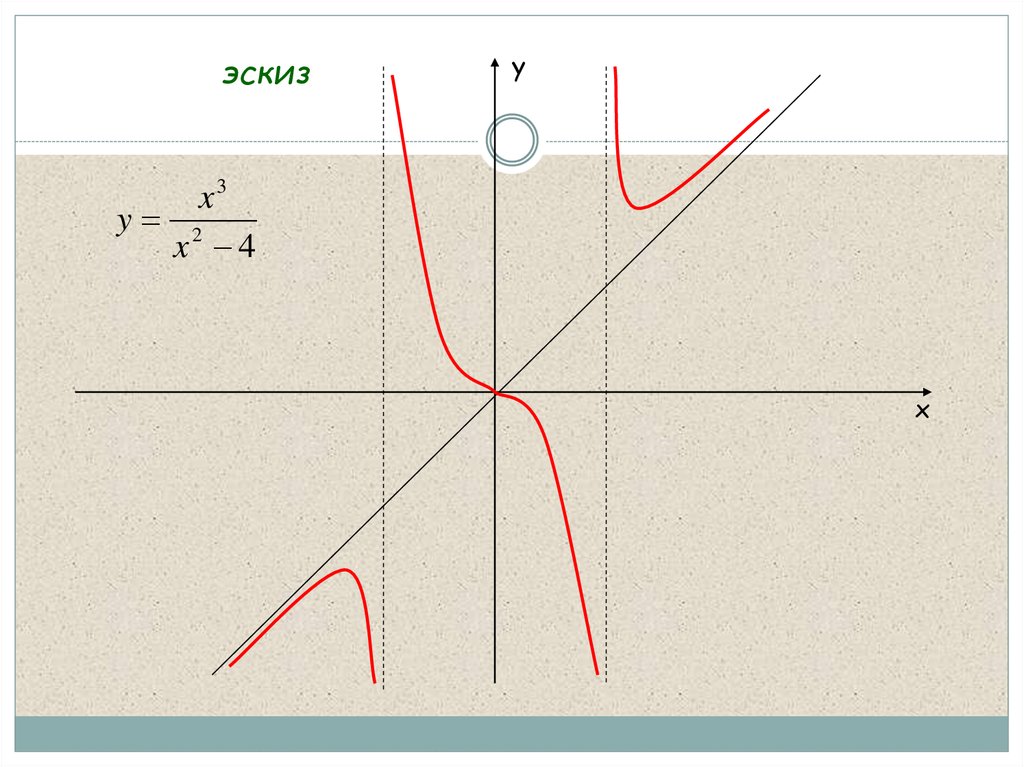
6. Исследовать функцию и построить её график

x3
y
x2 4
Исследовать функцию
и построить её график
D y ; 2 2; 2 2; ;
2.
3.
4.
Функция нечётная,
график симметричен
относительно начала
отсчёта.
Точки пересечения с осями:
с Оу: (0; 0); с Ох: (0; 0).
Промежутки
знакопостоянства
функции:
-
+
-2
+
0
-
2
х

7.

5. Вертикальные асимптоты:
х 2 и х 2, так как
эскиз
y
lim
x 2
lim
x 2
lim
x 2
lim
x 2
x3
8
,
2
x 4 0
x3
;
x2 4
lim
x 2
x3
.
x2 4
x3
8
.
x2 4
0
x3
;
x2 4
lim
x 2
x3
.
x2 4
-2
2
x

8. 6. Наклонные асимптоты

y x
k lim
x
3
эскиз
y
3
x
x
1.
2
x 2 4 x lim
x
4
x
x
b lim f x x lim f x x 0.
x
x
y x
x3
x3 x3 4x
4x
x
0 ;
lim
lim
2
2
x2 4
lim
x
4
x
4
x
x
x
4x
0 .
lim
2
x x 4
x

9. 7. Исследование на монотонность и наличие точек экстремума.

f x
x 4 12 x 2
x
2
4
f x 0, если
2
f x не существует, если
;
x
x 12 x 0
4
2
2
4
2
0,
x 2; x 2.
x 0; x 2 3.
2
f x
x 2 3 точка локального максимума
+
+
2
f 2 3 3 3
2 3
0
f x
x 2 3 точка локального минимума
f 2 3 3 3
-
+
2 3
+
2
х

10. Исследование на направление выпуклостей и наличие точек перегиба.

f x
8 x x 2 12
x
3
;
4
f x 0, если x 0.
2
f x
-
+
2
f x не существует, если
x 2, x 2
+
-
0
2
f x
0; f 0 точка перегиба
х

11.

эскиз
y
x3
y 2
x 4
x