Похожие презентации:
Частотные методы улучшения изображений. Лекция 3
1. Частотные методы улучшения изображений
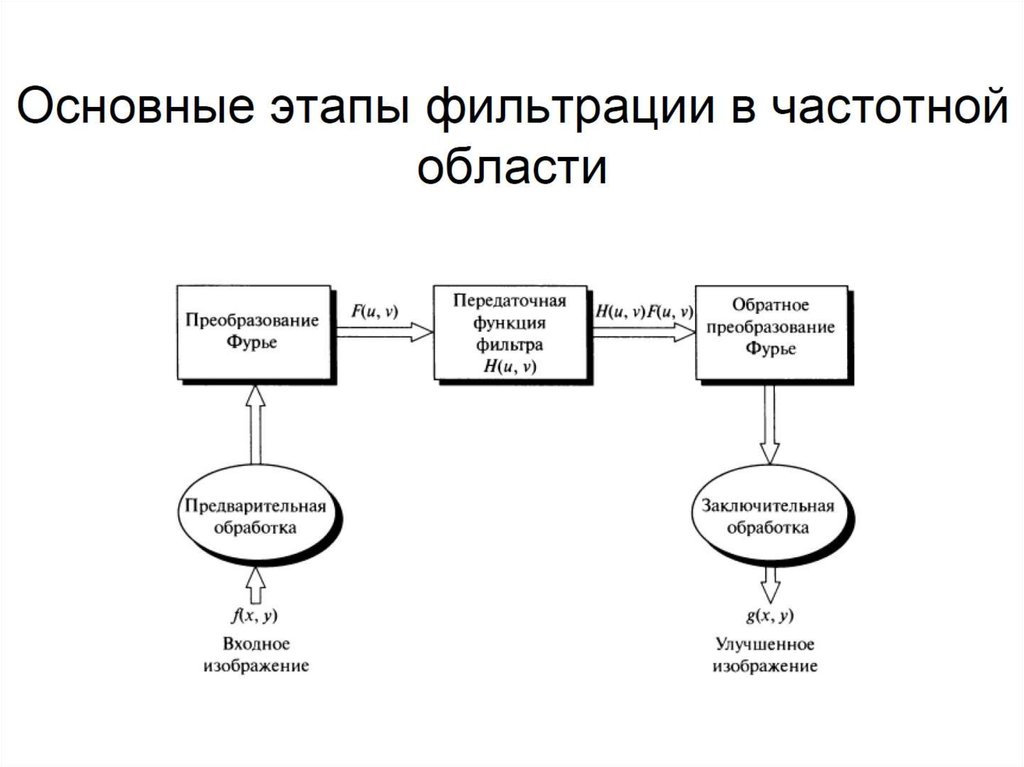
2. Линейная фильтрация в частотной области
- Линейная фильтрация сигналов и изображений можетосуществляться как в пространственной, так и в частотной
области.
- Низкочастотным составляющим соответствует
основное содержание изображения – фон и крупноразмерные
объекты,
- Высокочастотные составляющие – мелкоразмерные
объекты, мелкие детали крупных форм и шумовая
компонента.
- Традиционно для перехода между пространственной и
частотной пространствами используются методы, основанные
на преобразовании Фурье.
- В последние годы все большее применение находят
также методы, основанные на вейвлет-преобразовании
(wavelet-transform).
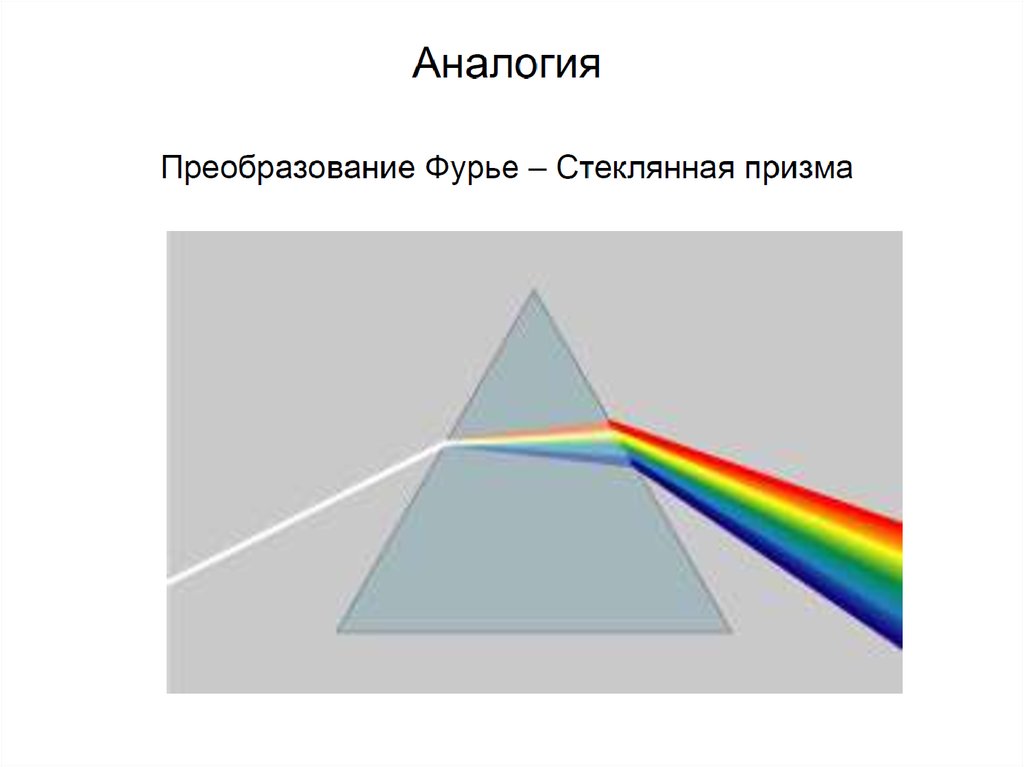
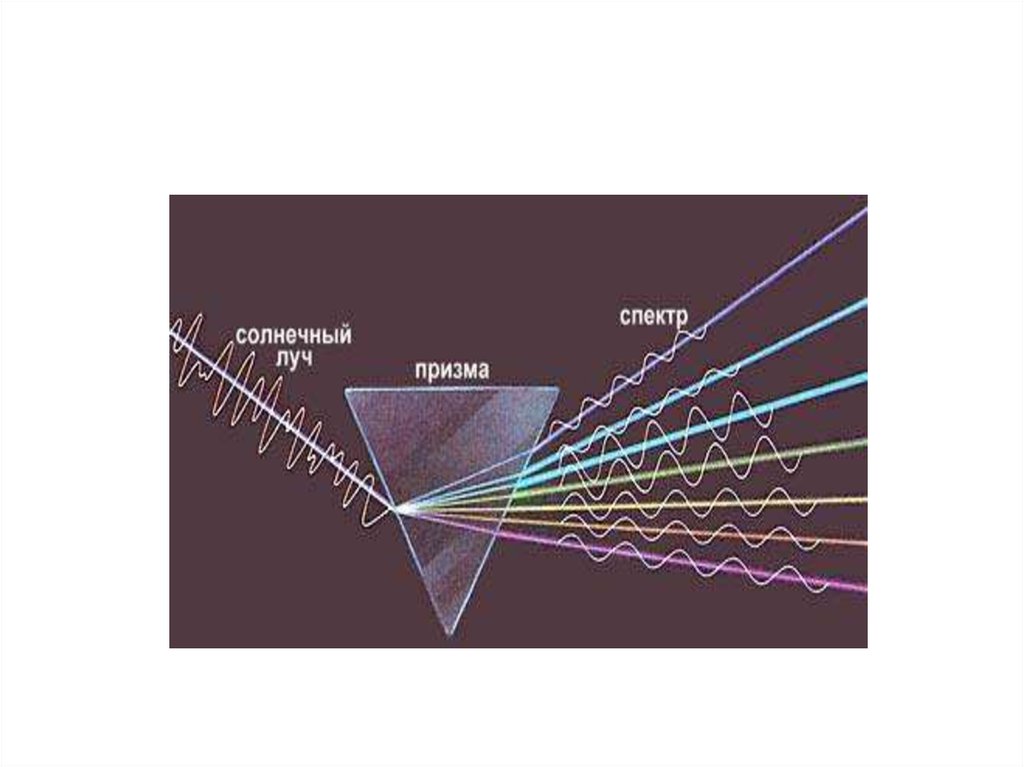
3. Преобразование Фурье
• Сигналы удобно анализировать,раскладывая на синусоиды (гармоники)
– Человек может различать высокие и низкие
частоты => требуется обработка сигналов
с учетом этого
• Преобразование Фурье – это
разложение функции на синусоиды
4.
5.
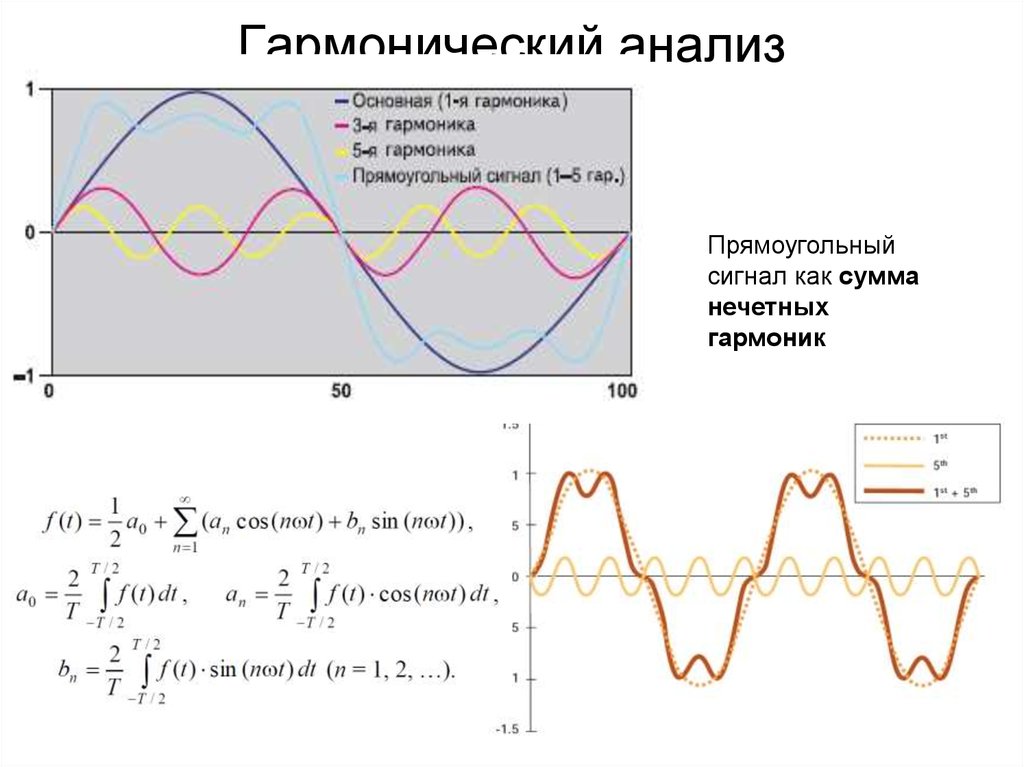
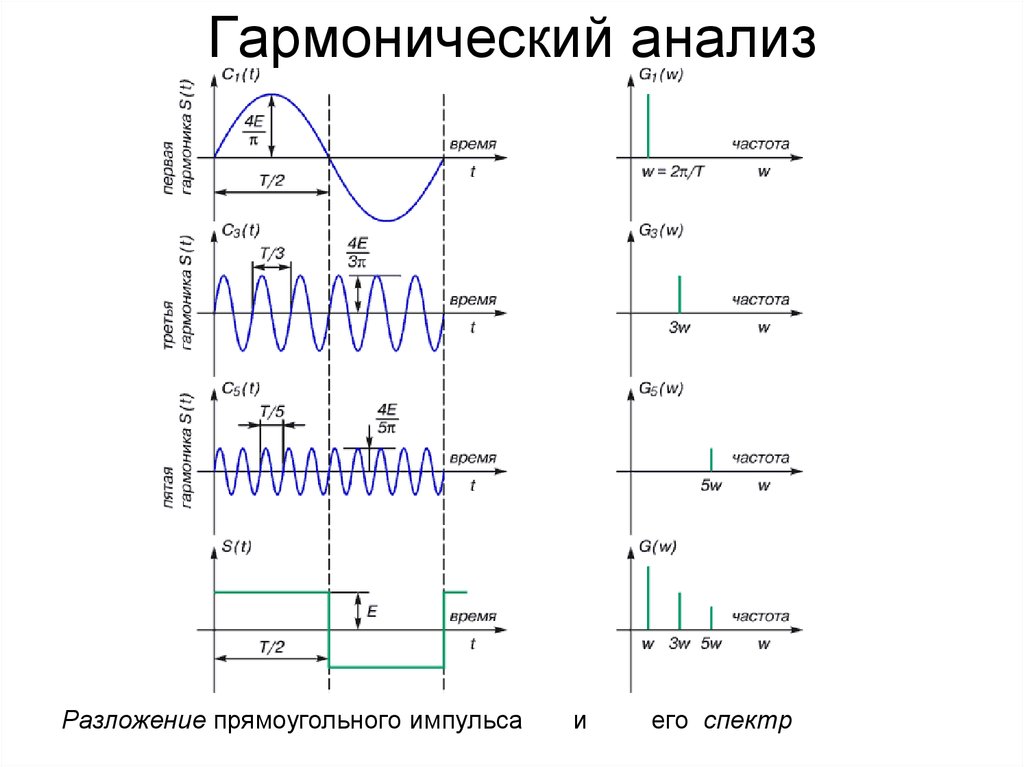
6. Гармонический анализ
Прямоугольныйсигнал как сумма
нечетных
гармоник
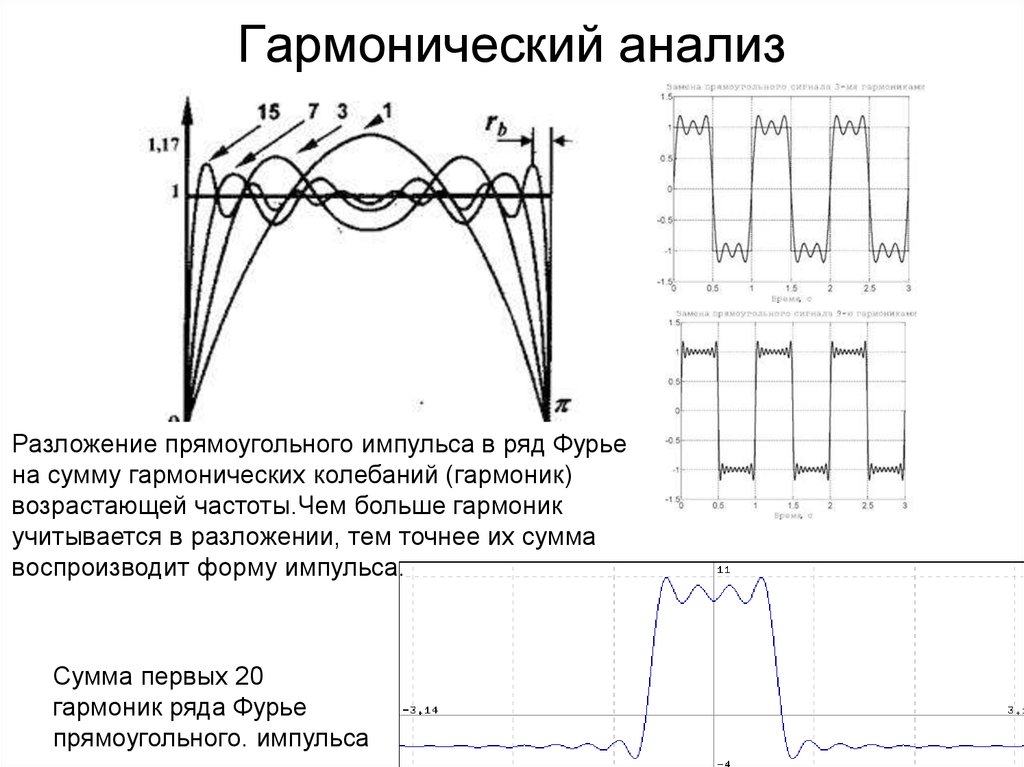
7. Гармонический анализ
Разложение прямоугольного импульса в ряд Фурьена сумму гармонических колебаний (гармоник)
возрастающей частоты.Чем больше гармоник
учитывается в разложении, тем точнее их сумма
воспроизводит форму импульса.
Сумма первых 20
гармоник ряда Фурье
прямоугольного. импульса
8. Гармонический анализ
Разложение прямоугольного импульсаи
его спектр
9.
10.
11.
12.
13.
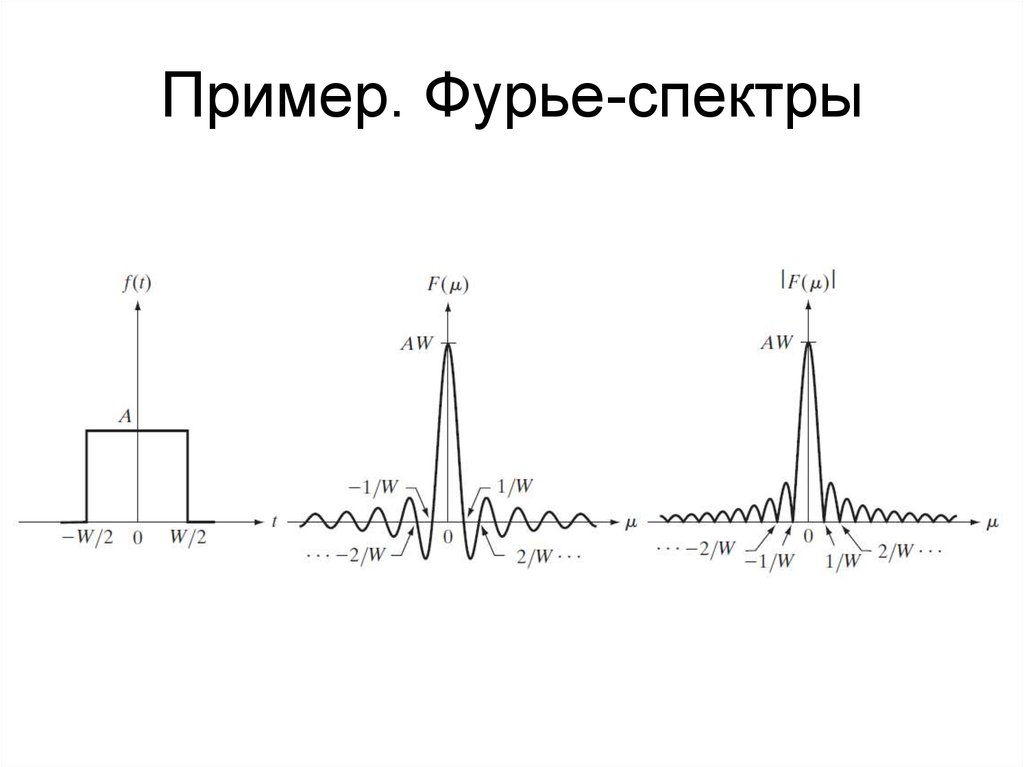
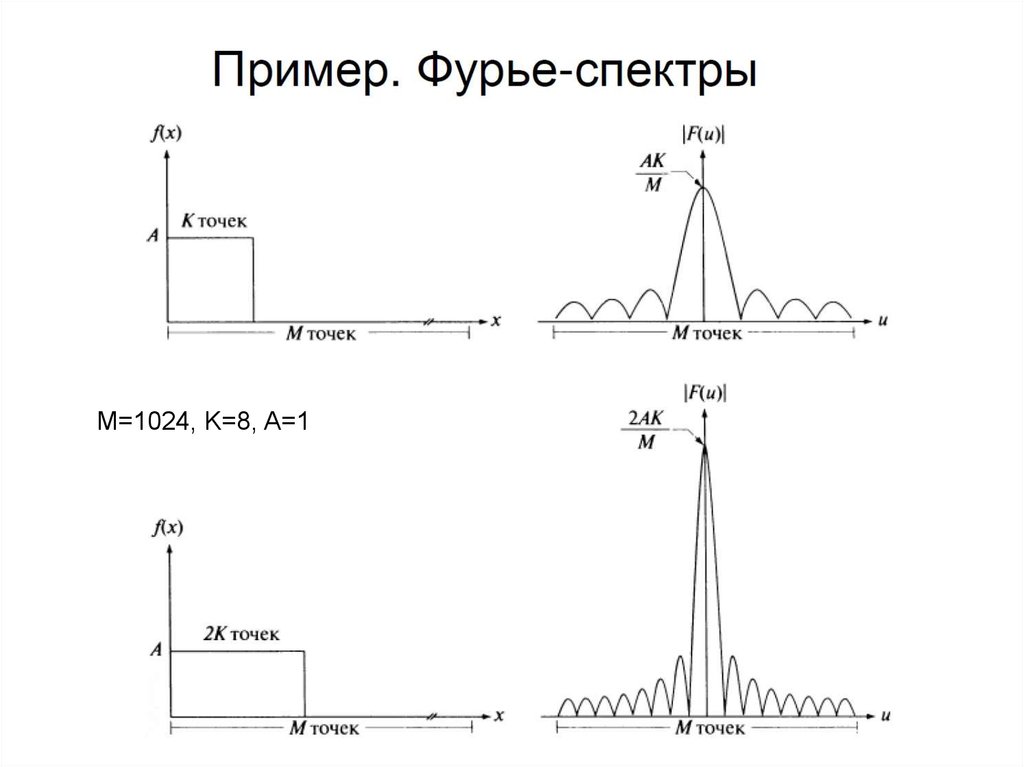
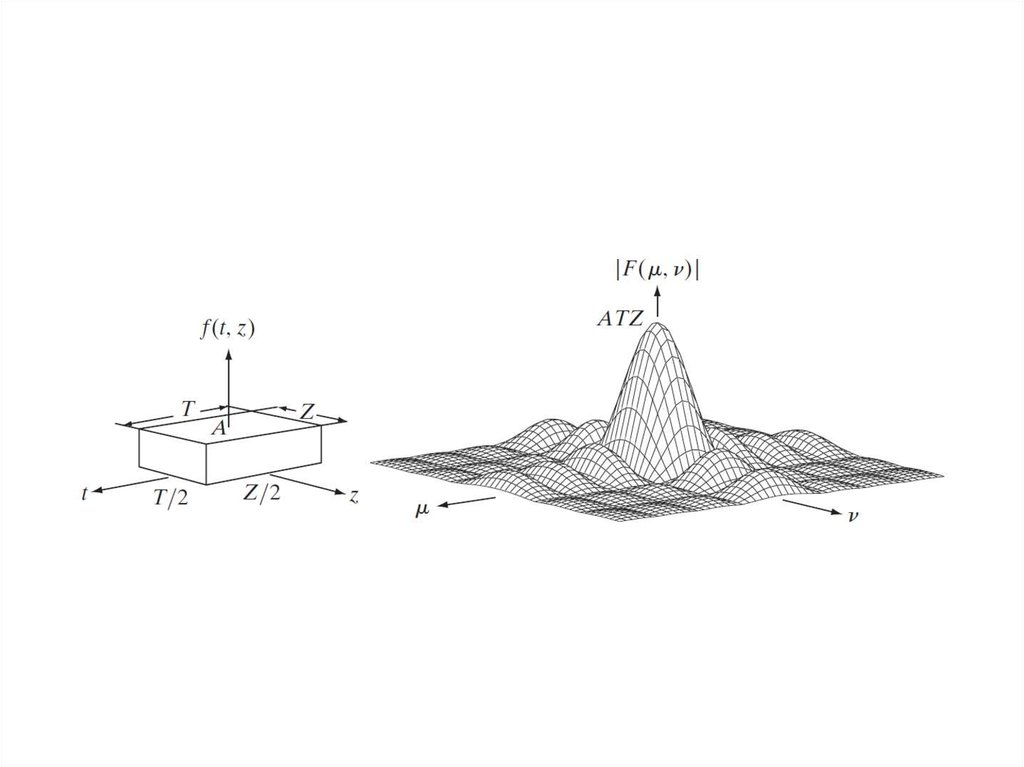
14. Пример. Фурье-спектры
15.
M=1024, K=8, A=116.
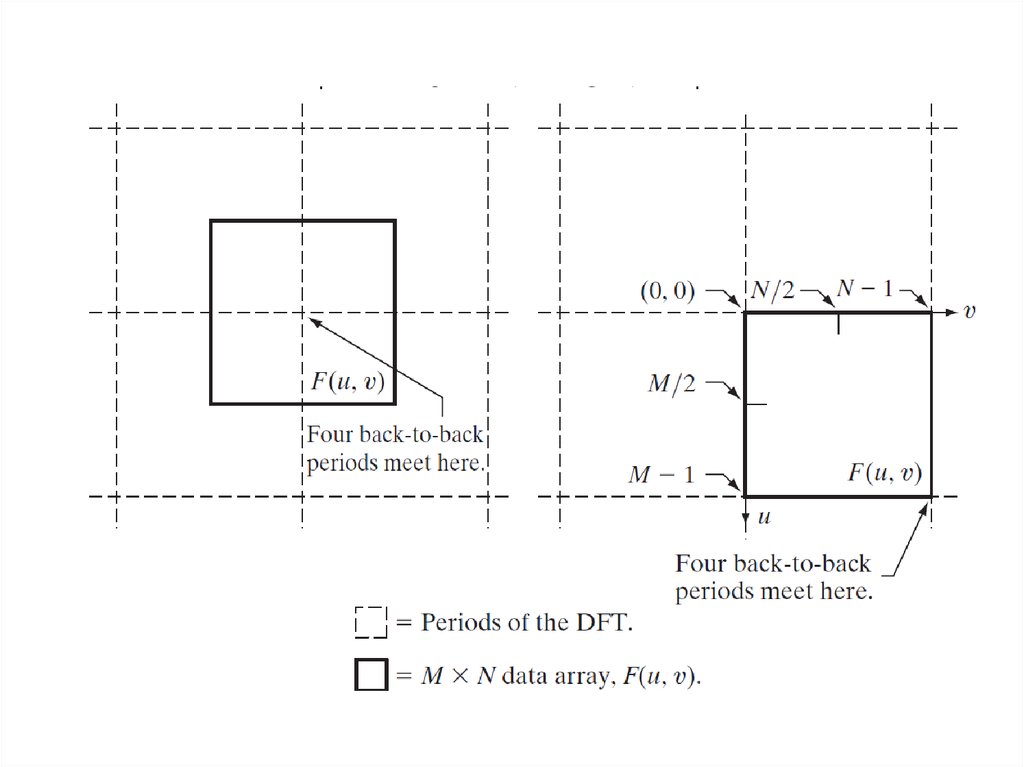
17. Двумерное преобразование Фурье
В случае обработки изображений компоненты двумерногопреобразования Фурье называют пространственными
частотами.
Важным свойством двумерного преобразования Фурье является
возможность его вычисления с использованием процедуры
одномерного БПФ.
1
1
F ( u, v )
N y 0 M
N 1
M 1
f ( x, y )e
x 0
2 jux
M
e
2 jvy
N
Здесь выражение в квадратных скобках есть одномерное
преобразование строки матрицы данных, которое может быть
выполнено с одномерным БПФ. Таким образом, для получения
двумерного преобразования Фурье нужно сначала вычислить
одномерные преобразования строк, записать результаты в
исходную матрицу и вычислить одномерные преобразования для
столбцов полученной матрицы.
18.
19.
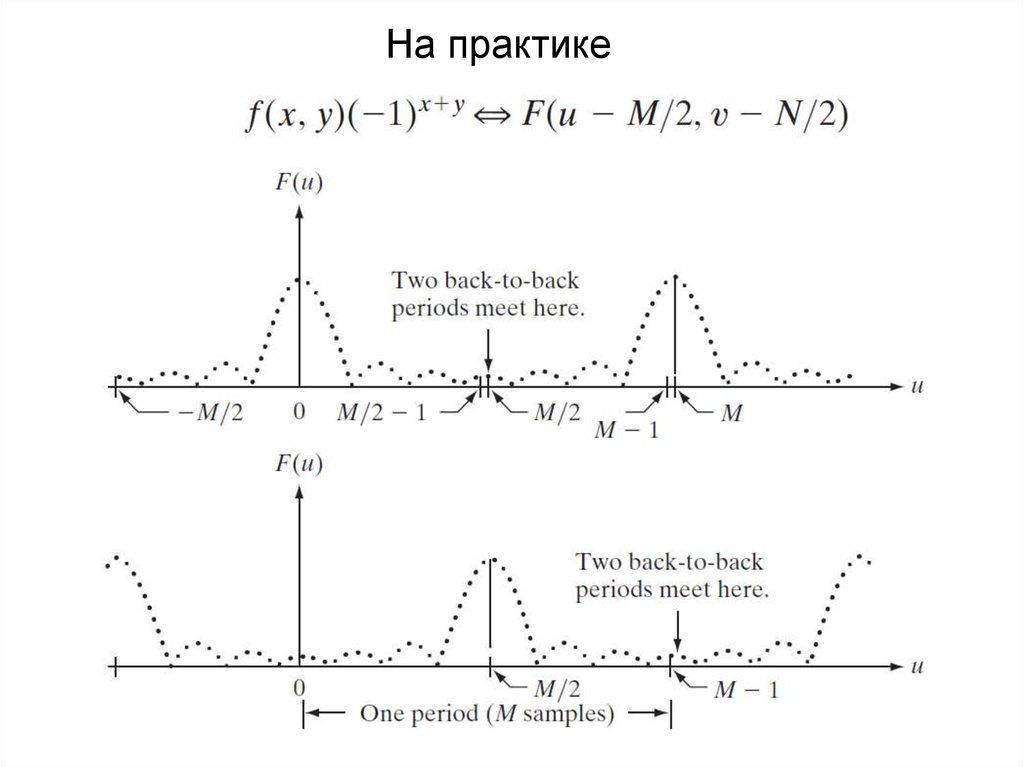
20. На практике
21.
22.
23.
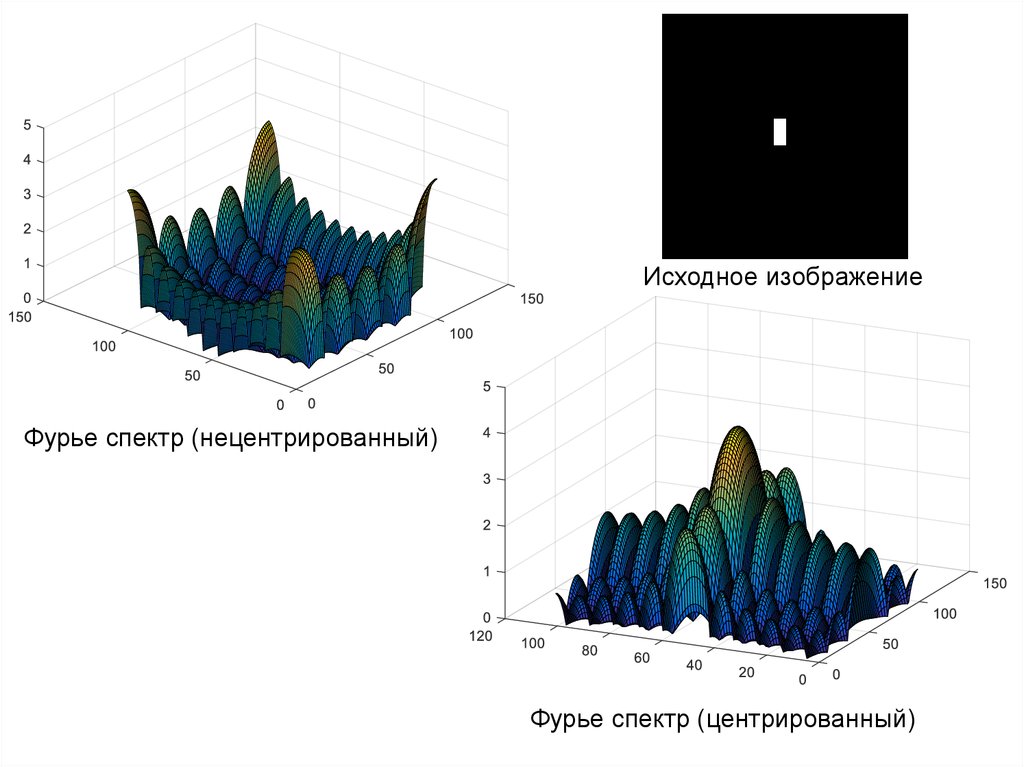
Исходное изображениеФурье спектр (нецентрированный)
Фурье спектр (центрированный)
24.
g=fft2(f)g=fftshift(g)
g1=log(1+abs(g))
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
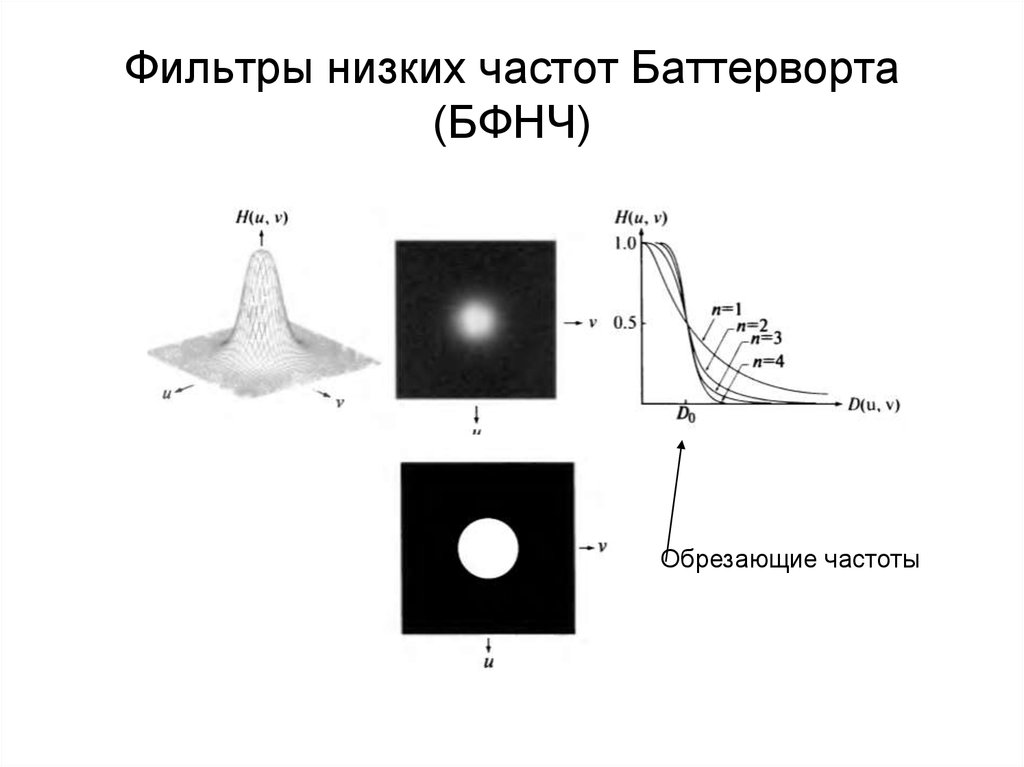
50. Фильтры низких частот Баттерворта (БФНЧ)
1H u, v
2n
1 D u, v / D0
D u, v D0
ИФНЧ
D u, v u M / 2 v N / 2
2
H u, v 0,5
БФНЧ
2 12
51. Фильтры низких частот Баттерворта (БФНЧ)
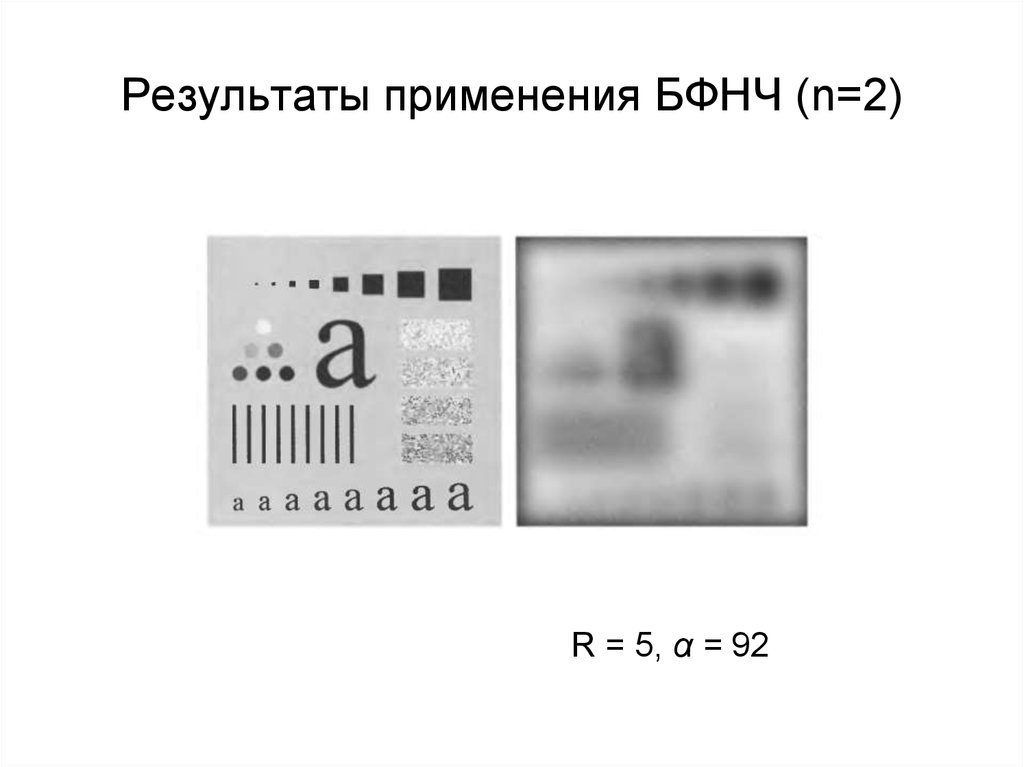
Обрезающие частоты52. Результаты применения БФНЧ (n=2)
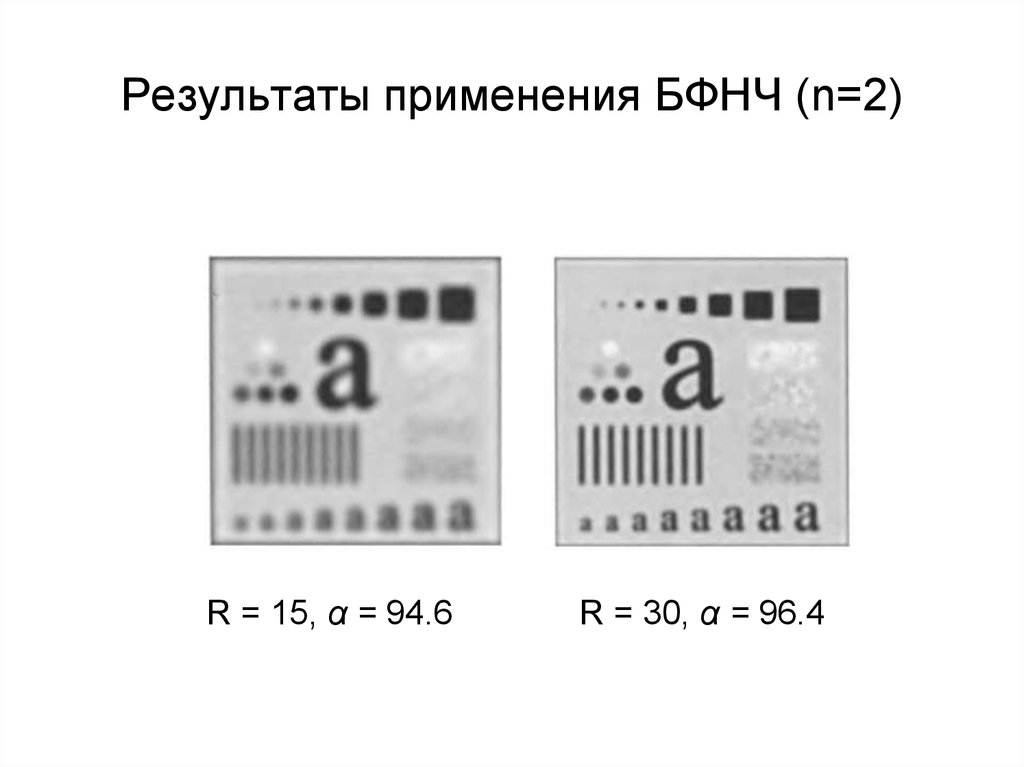
R = 5, α = 9253. Результаты применения БФНЧ (n=2)
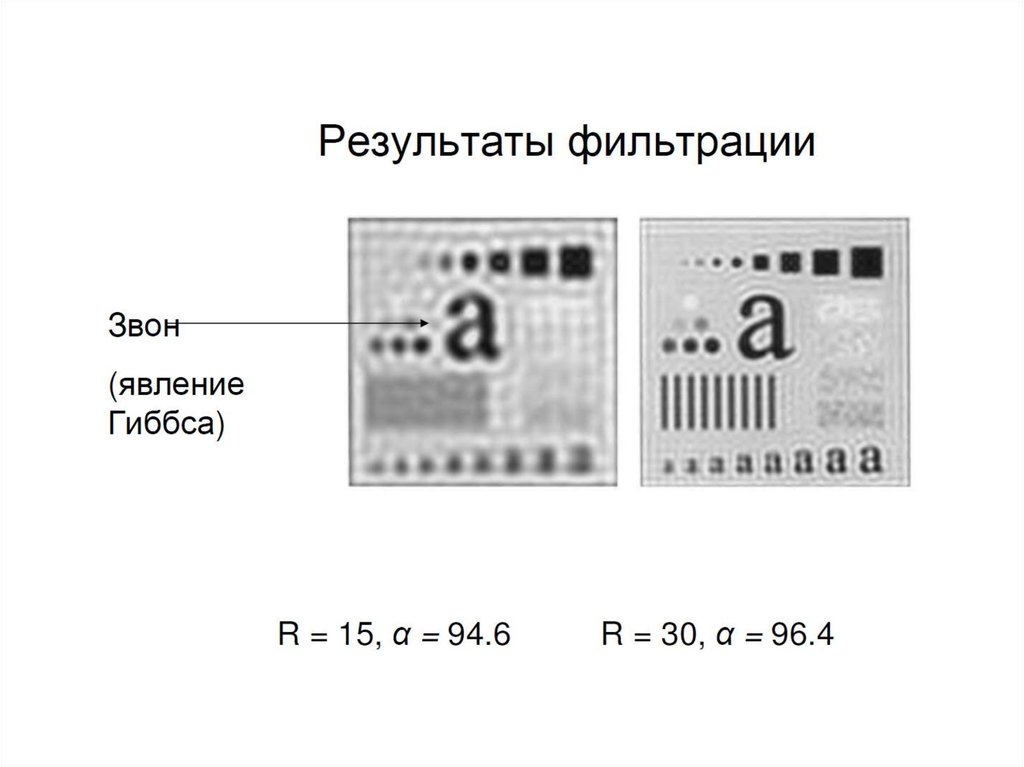
R = 15, α = 94.6R = 30, α = 96.4
54. Результаты применения БФНЧ (n=2)
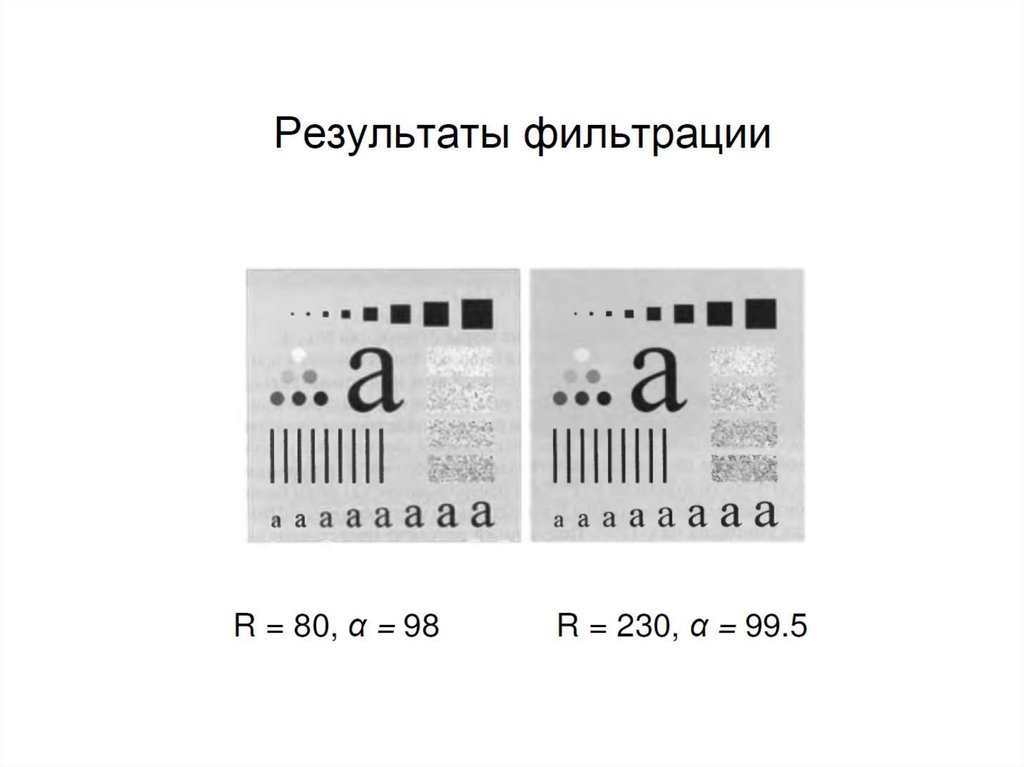
R = 80, α = 98R = 230, α = 99.5
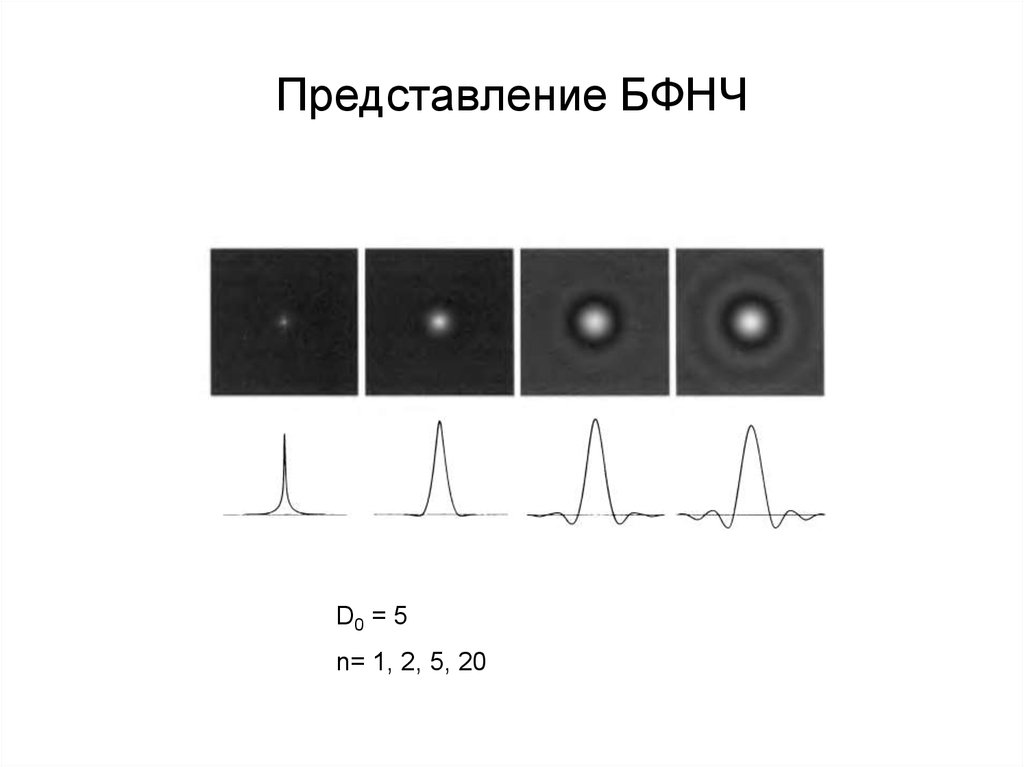
55. Представление БФНЧ
D0 = 5n= 1, 2, 5, 20
56. Сравнение БФНЧ (n=20 →∞) и ИФНЧ
БФНЧ (n=20)ИФНЧ
D0=5
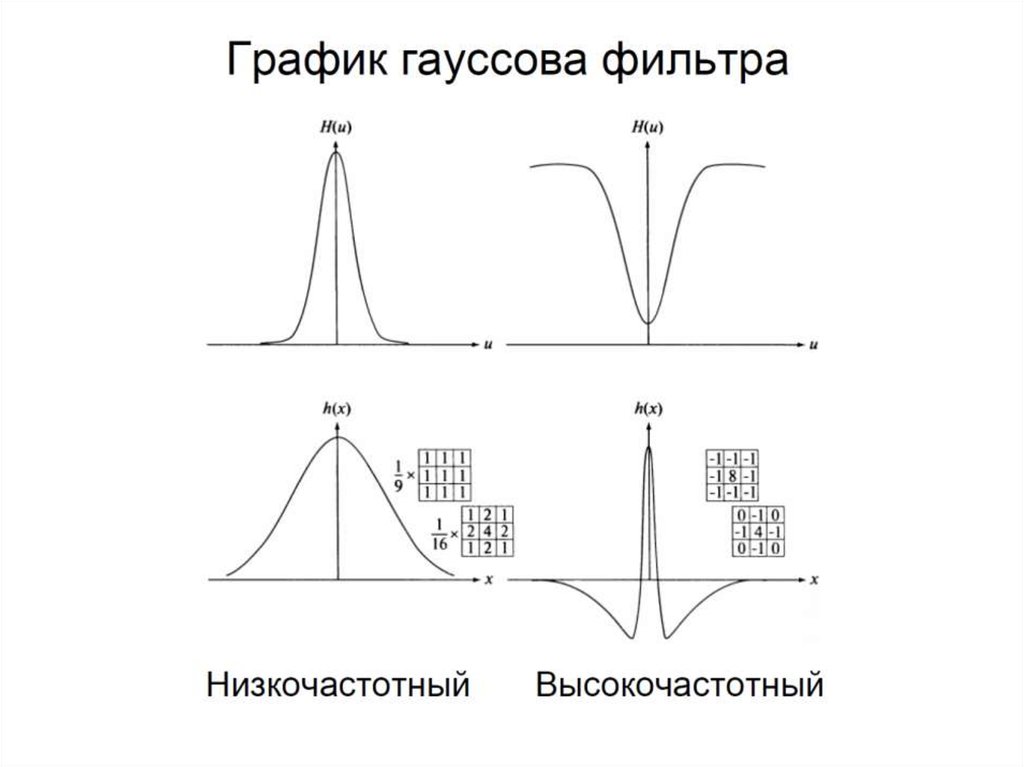
57. Гауссовы фильтры низких частот (ГФНЧ)
H u Aeu 2 / 2 2
H u, v e
D2 u ,v / 2 2
Одномерный
Двумерный
A=1
H u, v e
D2 u ,v / 2 D02
D u, v D0
H u, v 0,607
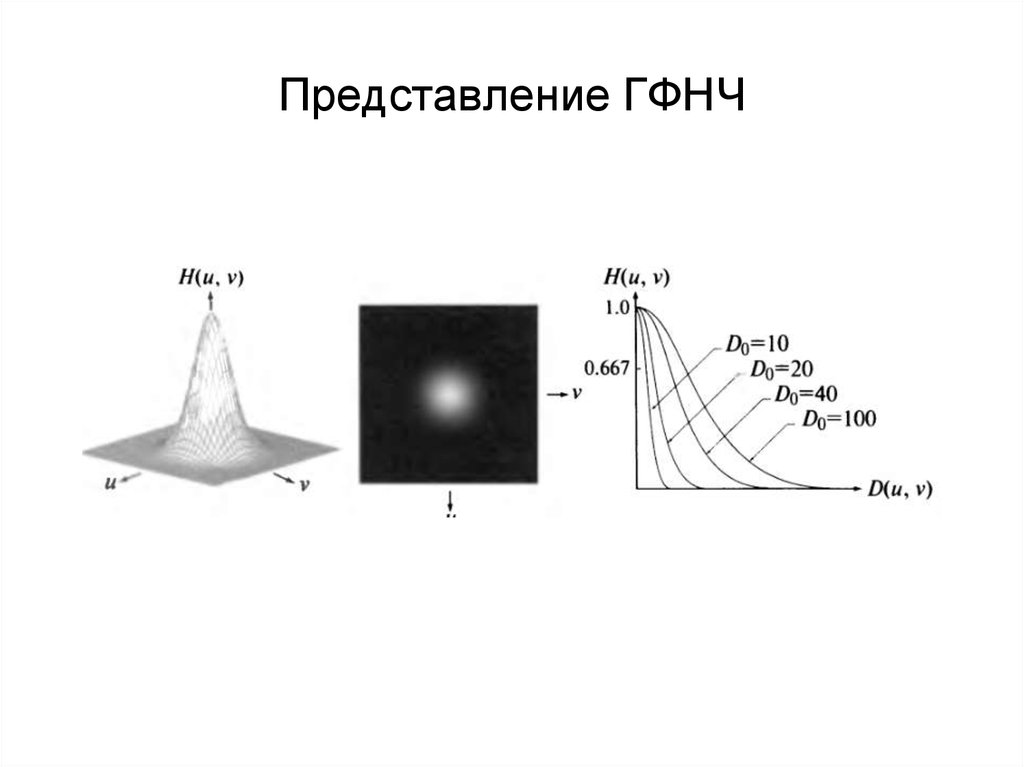
58. Представление ГФНЧ
59. Результаты применения ГФНЧ
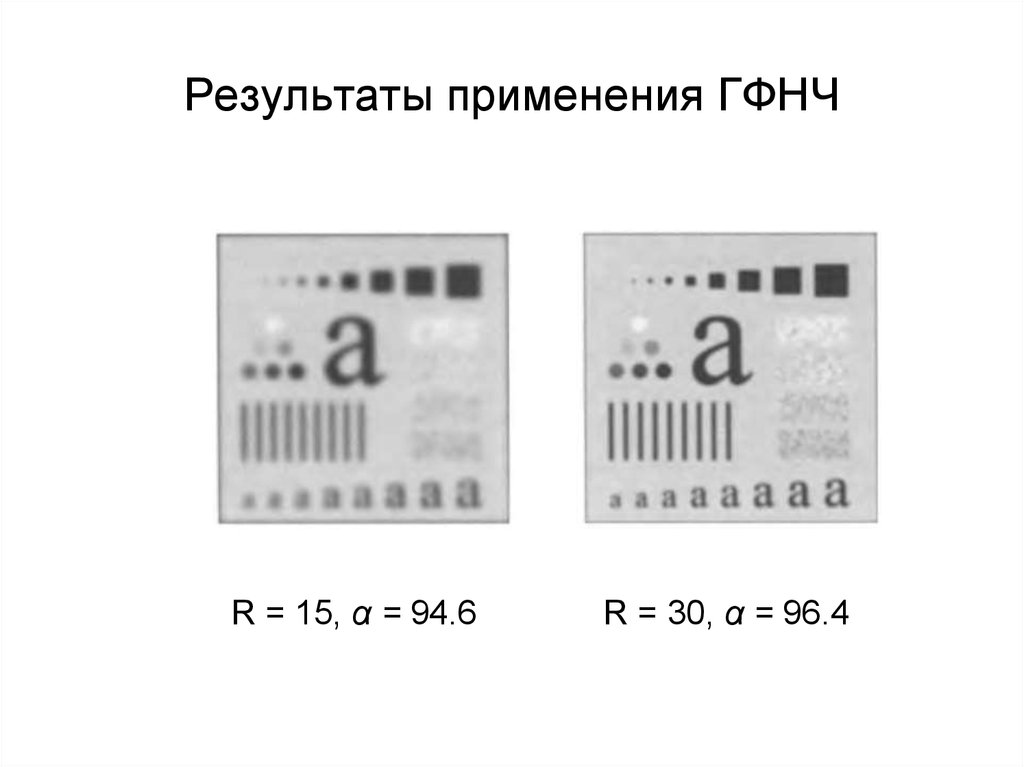
R = 5, α = 9260. Результаты применения ГФНЧ
R = 15, α = 94.6R = 30, α = 96.4
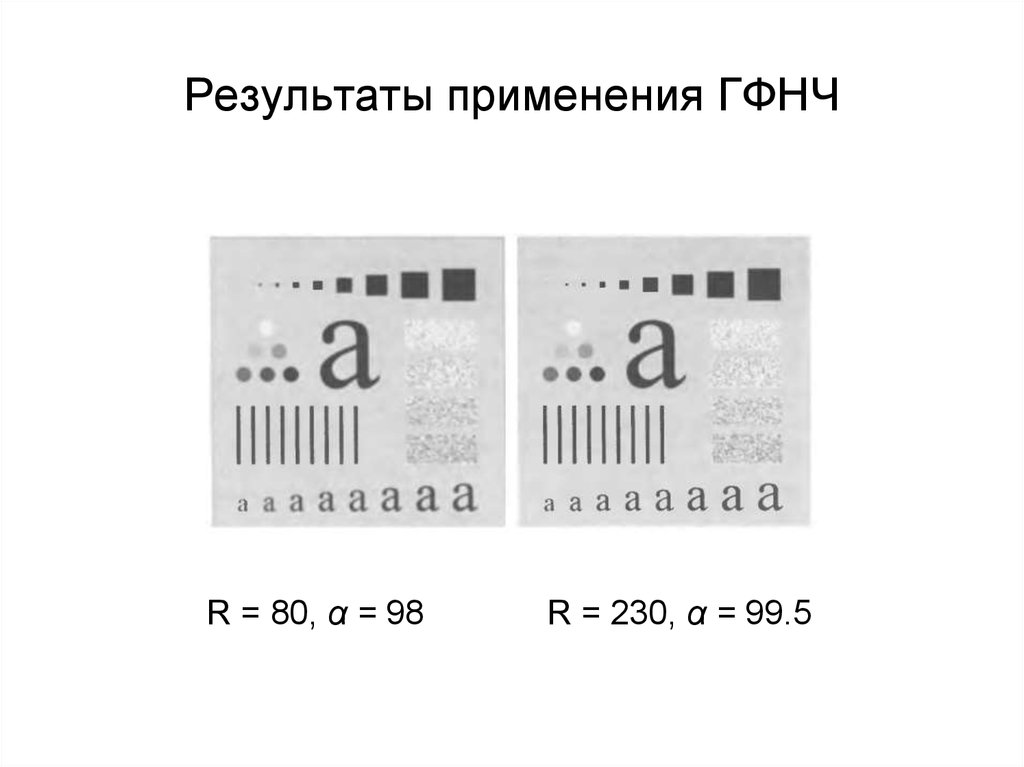
61. Результаты применения ГФНЧ
R = 80, α = 98R = 230, α = 99.5
62. Сравнение БФНЧ и ГФНЧ (D0=15)
R = 15, α = 94.6R = 15, α = 94.6
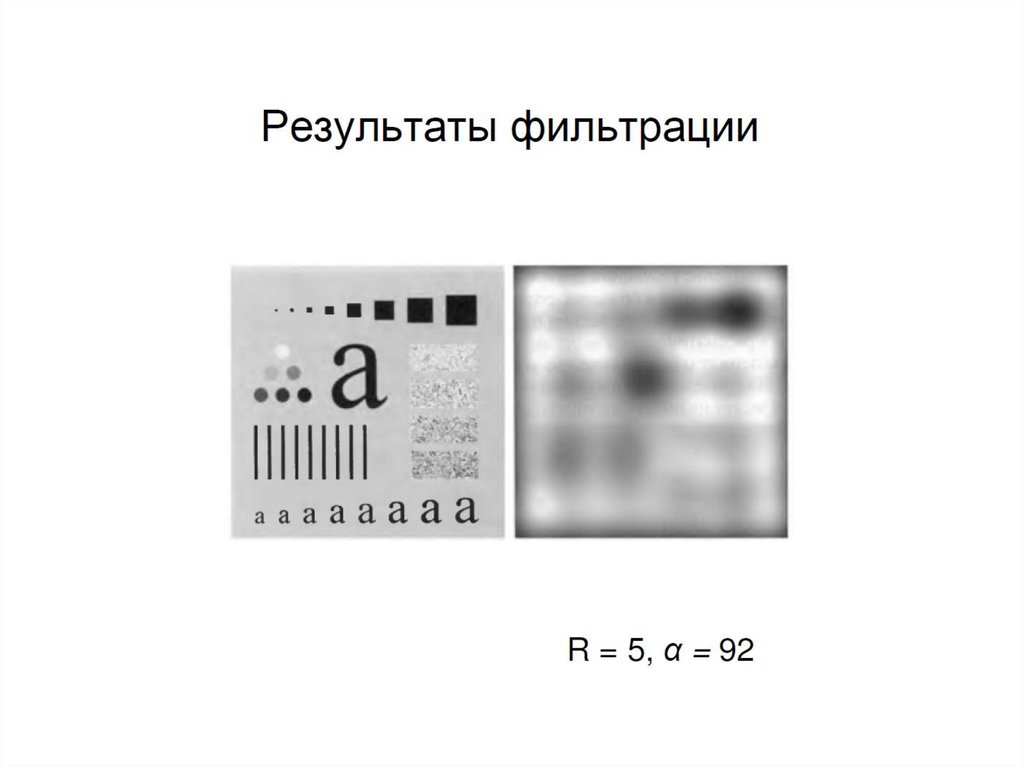
63. Примеры низкочастотной фильтрации в распознавании текста
ГФНЧ (D0=80) размер изображения 444 х 50864. Примеры низкочастотной фильтрации в полиграфии
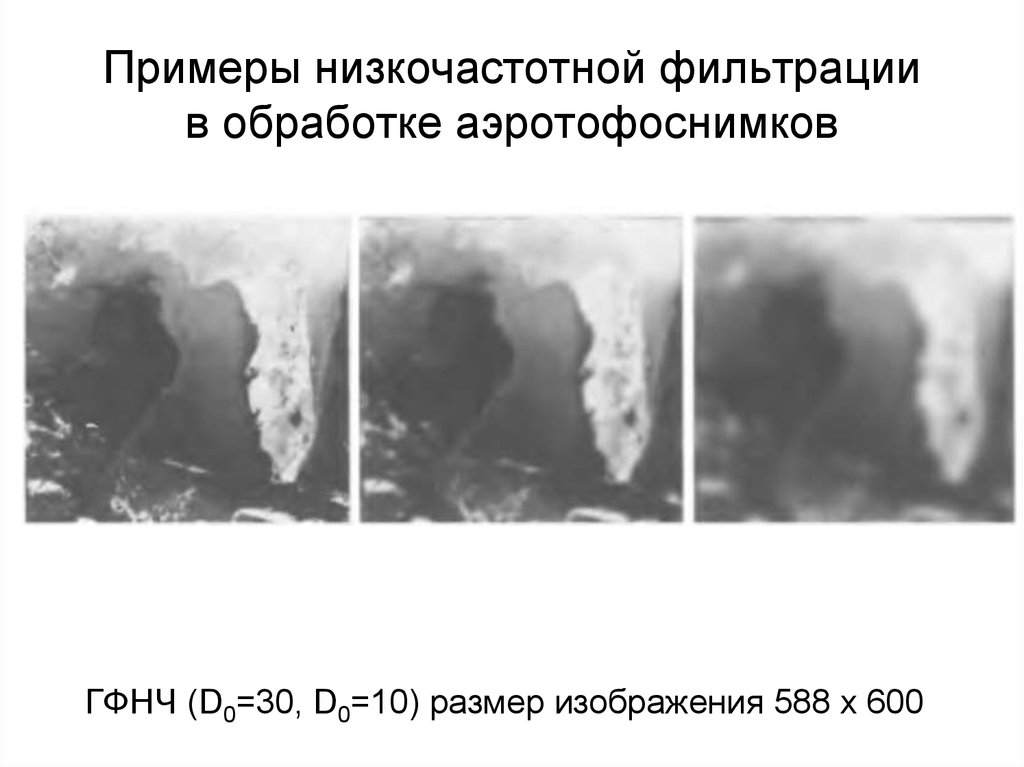
ГФНЧ (D0=80, D0=100) размер изображения 1028 х 73265. Примеры низкочастотной фильтрации в обработке аэротофоснимков
ГФНЧ (D0=30, D0=10) размер изображения 588 х 60066. Частотные фильтры повышения резкости
Рассматриваем центрально-симметричные фильтры нулевогофазового сдвига
Передаточная функция
H hp u, v 1 H lp u, v
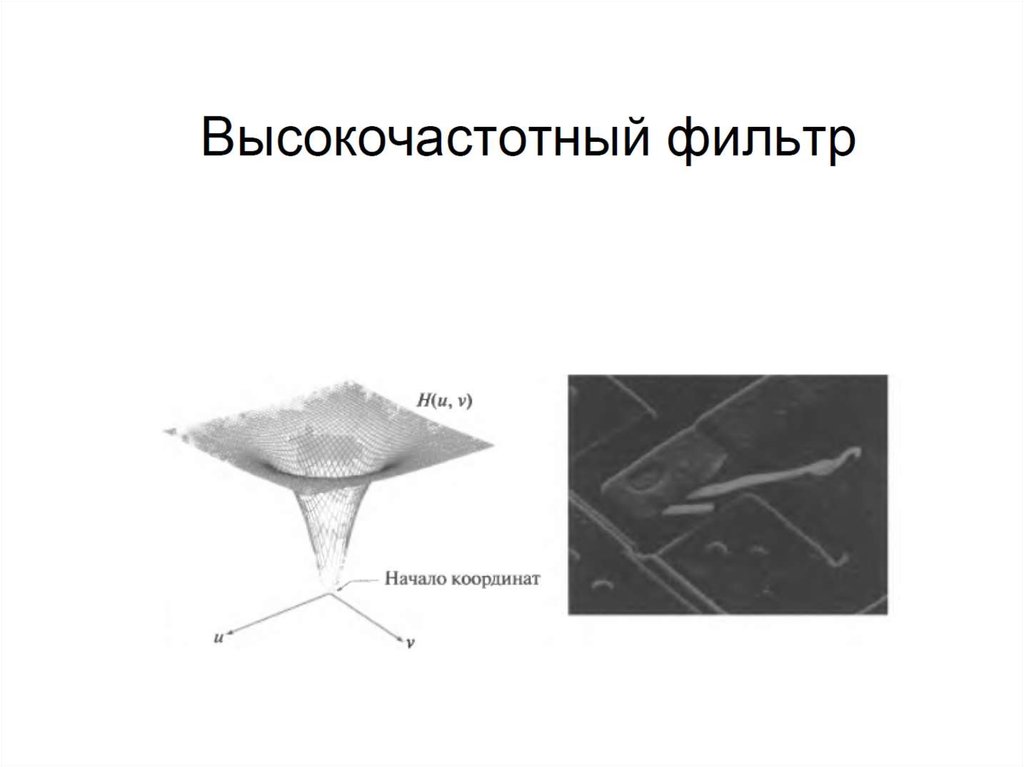
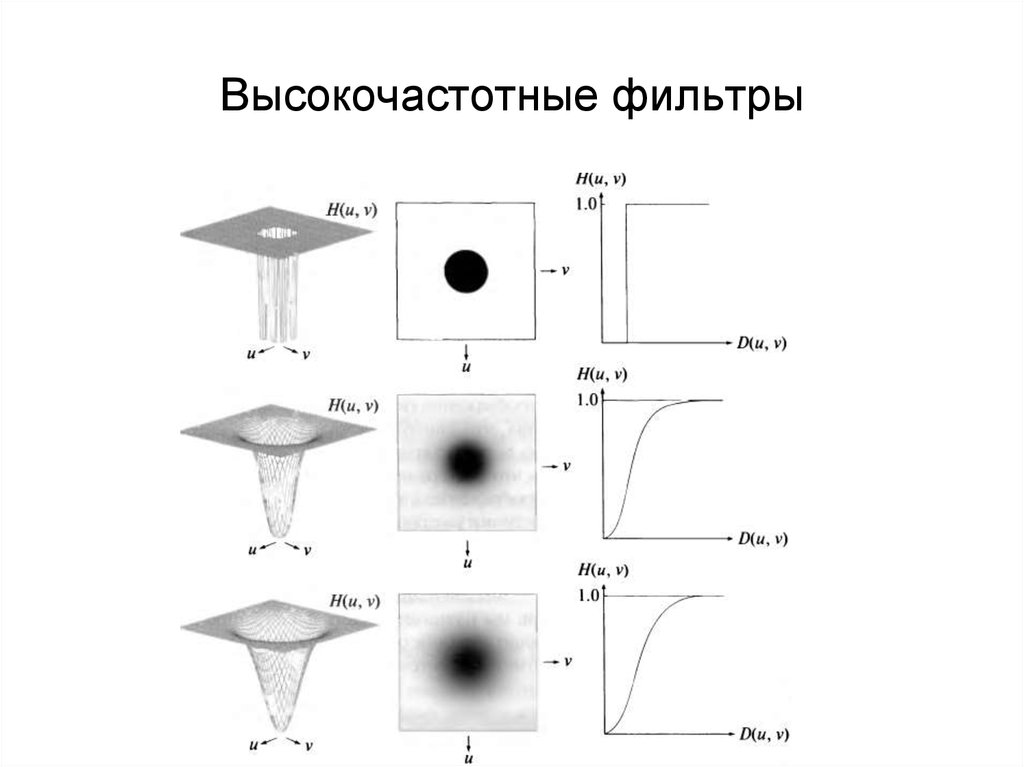
67. Высокочастотные фильтры
• Идеальные фильтры высоких частот – очень резкий• Фильтр Баттерворта – переходный (зависит от порядка)
• Гауссов фильтр – очень гладкий
68. Высокочастотные фильтры
69. Получение пространственного фильтра из частотного
1.2.
3.
Функция фильтра H(u,v) * (-1)u+v
Вычисляется обратное ДПФ
Вещественная часть * (-1)x+y
70. Идеальные фильтры низких частот (ИФВЧ)
0, при D u, v D0H u, v
1, при D u, v D0
D u, v u M / 2 v N / 2
2
2 12
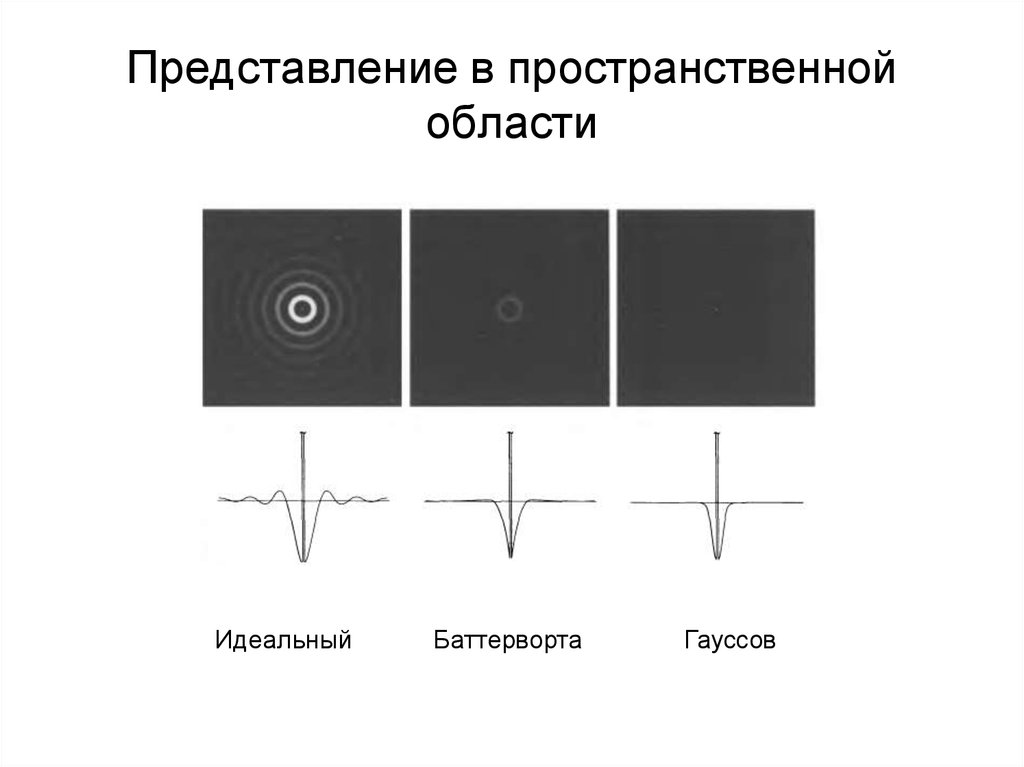
71. Представление в пространственной области
ИдеальныйБаттерворта
Гауссов
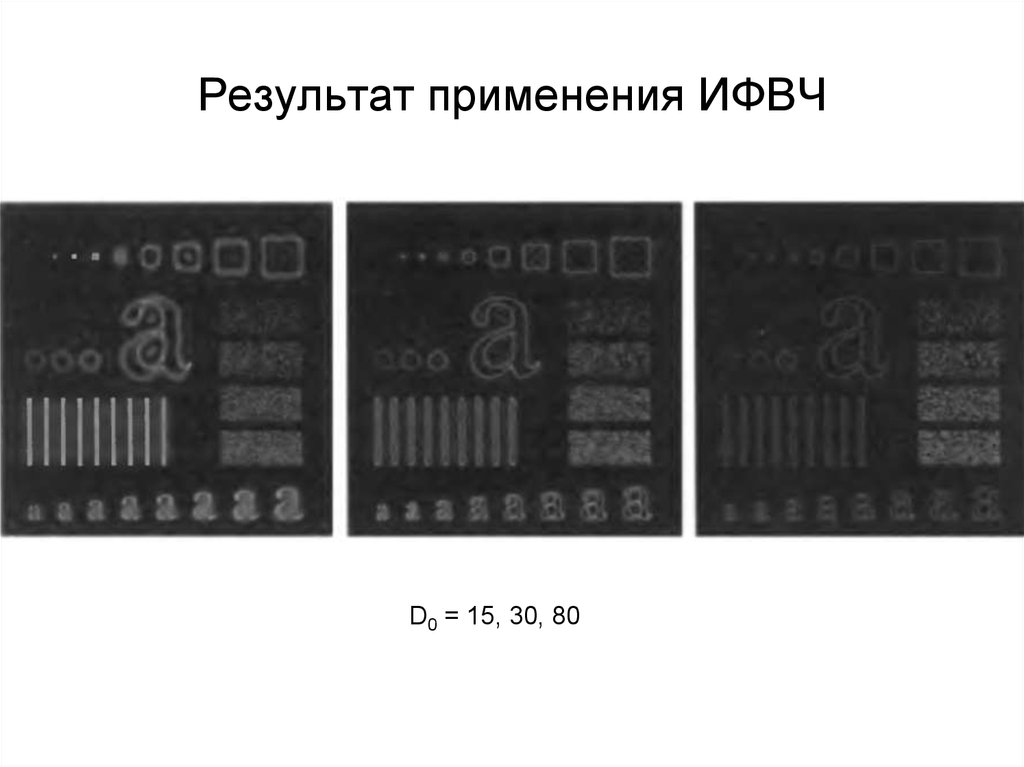
72. Результат применения ИФВЧ
D0 = 15, 30, 8073. Фильтры высоких частот Баттерворта (БФВЧ)
H u, v1
2n
1 D0 / D u, v
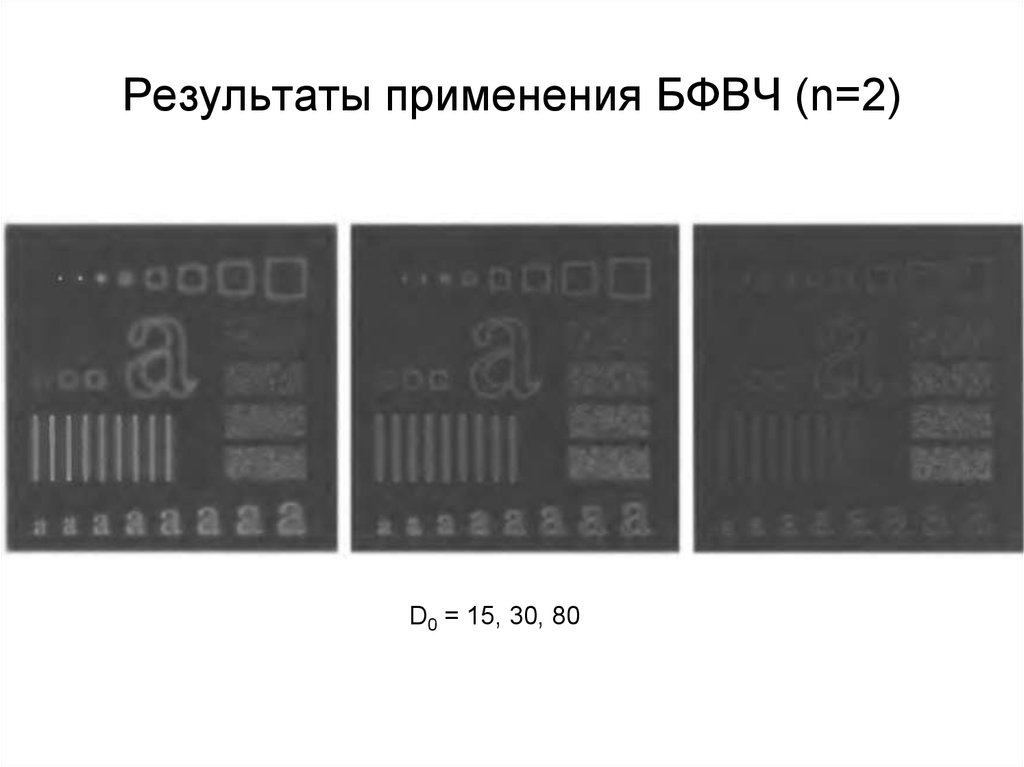
74. Результаты применения БФВЧ (n=2)
D0 = 15, 30, 8075. Гауссовы фильтры высоких частот (ГФВЧ)
H u, v 1 eD 2 u ,v / 2 D02
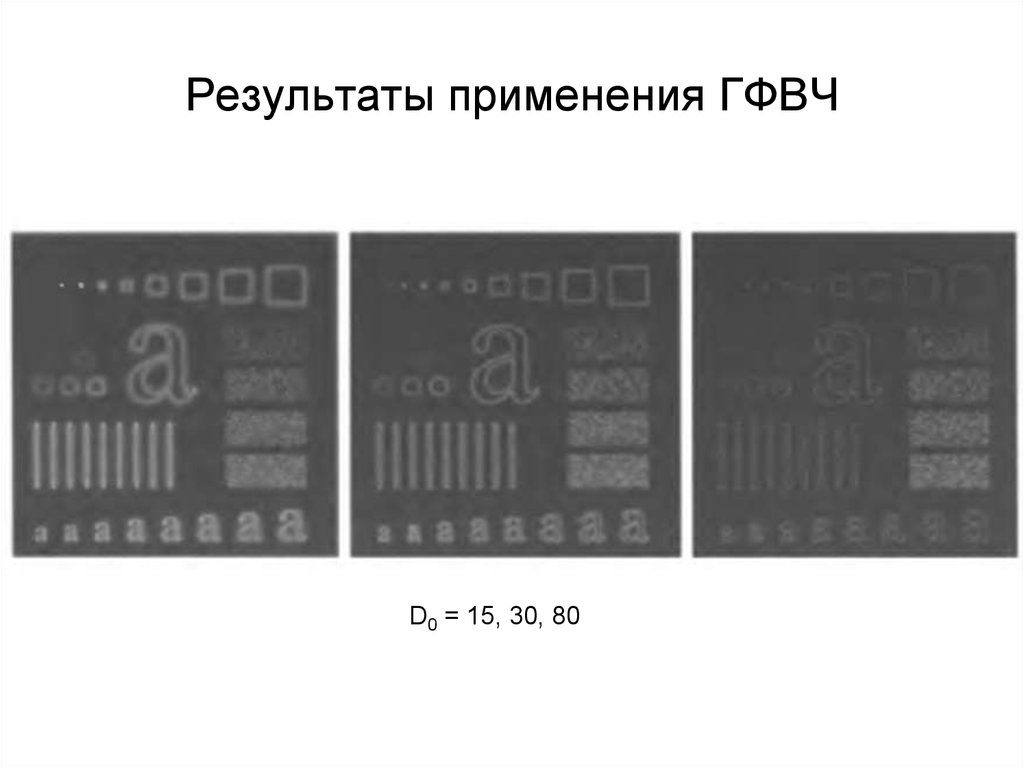
76. Результаты применения ГФВЧ
D0 = 15, 30, 8077. Лапласиан в частотной области
d n f xn
iu
F u
n
dx
2 f x, y 2 f x, y
2
2
2
2
iu
F
u
,
v
iv
F
u
,
v
u
v
F u, v
2
2
y
x
2 f x, y u 2 v 2 F u, v
H u, v u 2 v 2
78. Сдвиг центра передаточной функции
H u, v u 2 v 2H u, v u M / 2 v N / 2
2
2
79. Результат применения дискретного оператора Лапласа в частотной области
22
2
1
f x, y u M / 2 v N / 2 F u, v
2 f x, y u M / 2 v N / 2 F u, v
2
2
80. Представление Лапласиана
81. Для получения улучшенного изображения
вычитаем Лапласиан (изображение полученное сиспользованием частотного фильтра Лапаласа) из
оригинала
g x, y f x, y 2 x, y
82. Вариант использования одного фильтра
H u, v 1 u M / 2 v N / 22
2
2 f x, y 1 1 u M / 2 v N / 2 F u, v
2
2
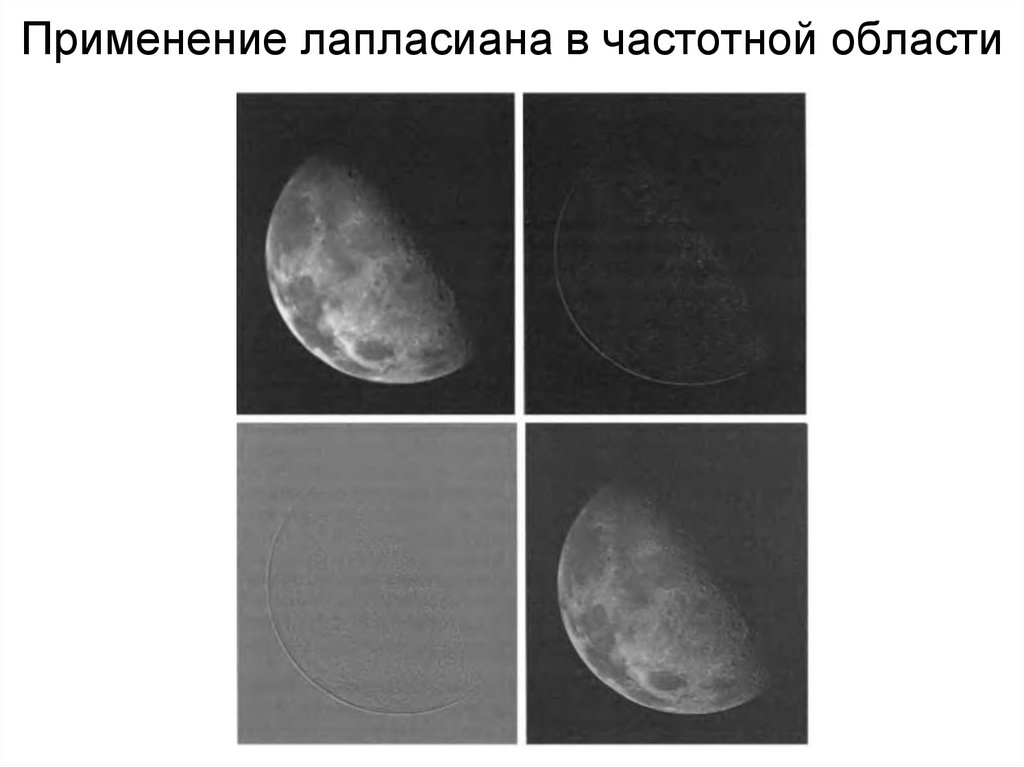
83. Применение лапласиана в частотной области
84. Вариации фильтров
• Нерезкое маскирование• Высокочастотная фильтрация с подъемом частотной
характеристики
• Фильтрация с усилением высоких частот
85. Общее свойство ФВЧ
Среднее значение яркости фона близко к 086. В случае лапласиана
прибавляется исходное изображение к результатуфильтрации
87. Такой подход называется
высокочастотная фильтрация с подъемом частотнойхарактеристики
обобщение метода нерезкого маскирования
88. Нерезкое маскирование
резкое маскирование = оригинал – сглаженная копияf hp x, y f x, y f lp x, y
89. Высокочастотная фильтрация с подъемом частотной характеристики
f hb x, y Af x, y f lp x, yf hb x, y A 1 f x, y f x, y f lp x, y
f hb x, y A 1 f x, y f hp x, y
90. Нерезкое маскирование в частотной области
H hp u, v 1 H lp u, v91. Фильтрация с подъемом частотной характеристики
H hb u, v A 1 H hp u, v92. Результат ФВЧ с подъемом частотной характеристики
ЛапласианA=2.0
A=2.7
93. Сравнение частотного лапласиана с пространственным
частотныйпространственный
94. Фильтрация с усилением высоких частот
H hfe u, v a bH hp u, v0.25 ≤ a ≤ 0.50
1. 5 ≤ b ≤ 2.5
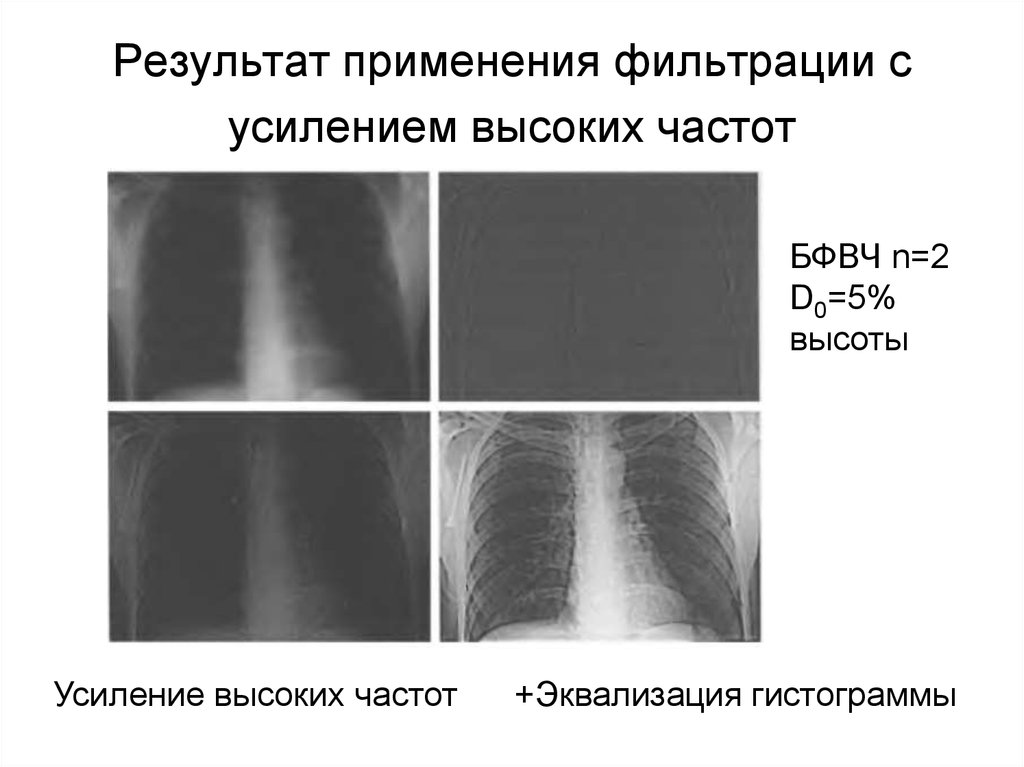
95. Результат применения фильтрации с усилением высоких частот
БФВЧ n=2D0=5%
высоты
Усиление высоких частот
+Эквализация гистограммы
96. Гомоморфная фильтрация
Сжатие яркостного диапазона и усиление контрастаЕще один вариант представления изображения
f x, y i x, y r x, y
97. Сложности частотной обработки
f x, y i x, y r x, yРассмотрим величину
z x, y ln f x, y ln i x, y ln rf x, y
Тогда
z x, y ln f x, y i x, y r x, y
или
Z u, v Fi u, v Fr u, v
98. Применим фильтрацию
S u, v H u, v Z u, v H u, v Fi u, v H u, v Fr u, vВ пространственной области имеем
s x, y 1 S u, v 1 H u, v Fi u, v 1 H u, v Fr u, v
s x, y i x, y r x, y
g x, y e s x , y ei x , y e r x , y i0 x, y r0 x, y
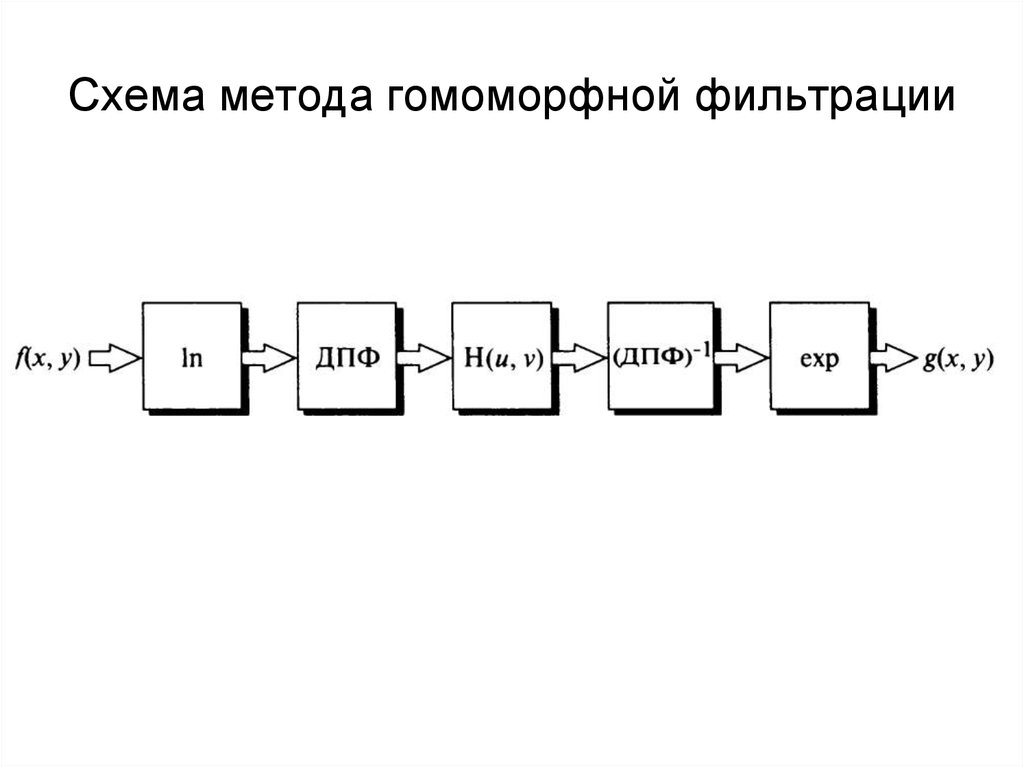
99. Схема метода гомоморфной фильтрации
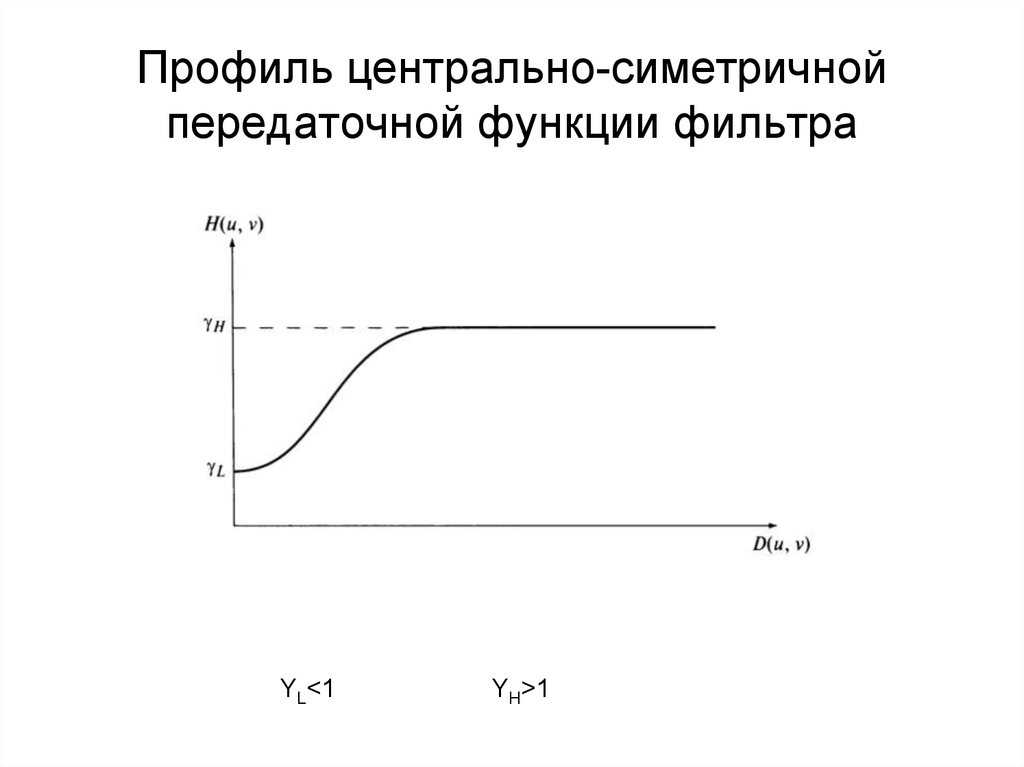
100. Профиль центрально-симетричной передаточной функции фильтра
ΥL<1ΥH>1
101. Аппроксимация модифицированным ГФВЧ
H u, v H L 1 e c D2
u ,v / D02
Похож на фильтр усиления высоких частот
L



































































 Информатика
Информатика








