Похожие презентации:
Интеграл. Урок обобщающего повторения
1. Интеграл
Урокобобщающего
повторения
2. План:
Создателиинтегрального исчисления.
Основные определения и формулы.
Нахождение первообразных.
Вычисление интегралов.
Вычисление площадей криволинейных
трапеций.
3. Ц - С
Ц-СФункция
Интеграл
Первообразная функции
Площадь криволинейной трапеции
Интегрирование – это операция нахождения
первообразной данной функции
Исаак Ньютон и Готфрид Лейбниц –
создатели интегрального исчисления
4. 1.
Создателиинтегрального
исчисления.
5. Исаак Ньютон (1643 – 1727)
Английский математик,физик, астроном, механик,
член Лондонского
королевского общества
(английской Академии
наук), член парламента,
директор монетного двора.
Разработал
дифференциальное и
интегральное исчисления,
открыл закон всемирного
тяготения, сформулировал
основные законы
механики.
6. Готфрид Вильгельм Лейбниц (1646 – 1716)
Немецкий философ, физик,математик, языковед,
основатель Берлинского
научного общества
(позднее – Академии
наук). По просьбе Петра I
разработал проект
развития образования
России. Создал
интегральное и
дифференциальное
исчисления, занимался
введением
математической
символики.
7. 2.
Основныеопределения и формулы.
8. Какая функция называется первообразной?
Функция F(х) называетсяпервообразной для функции f(х)
на некотором промежутке, если
для всех х из этого промежутка
F′(х) = f(х).
9. По какой формуле находят все первообразные для функции?
Если F(х) – некотораяпервообразная для f(х), то все
первообразные для функции f(х)
находятся по формуле F(х) + С,
где С – любая постоянная.
10. Как обозначают интеграл?
b∫ f (x) dx
а
11. Какой формулой пользуются для вычисления интегралов?
b∫
f (x) dx = F (b) – F (a)
a
b
∫
a
b
f (x) dx = F (x)
a
12. 3.
Нахождениепервообразных.
13. Найти все первообразные для функций:
x³ ;х + 3;
6x² – 2x;
4x³ + 3x²;
sin x;
cos x;
(x + 1)²;
(2x – 5)³ .
14. 4.
Вычислениеинтегралов.
15. Записать математическими символами и вычислить:
Интеграл от нуля до трехтри икс квадрат де икс.
Интеграл
от минус двух до двух
два икс де икс.
16. 5.
Вычисление площадейкриволинейных трапеций.
17. Найти площадь криволинейной трапеции, ограниченной прямыми х = 3, х = 4, и графиком функции у = х²
1.Построим график функцииу = х² и прямые х=3, х=4.
2. Вычислим площадь
полученной фигуры.









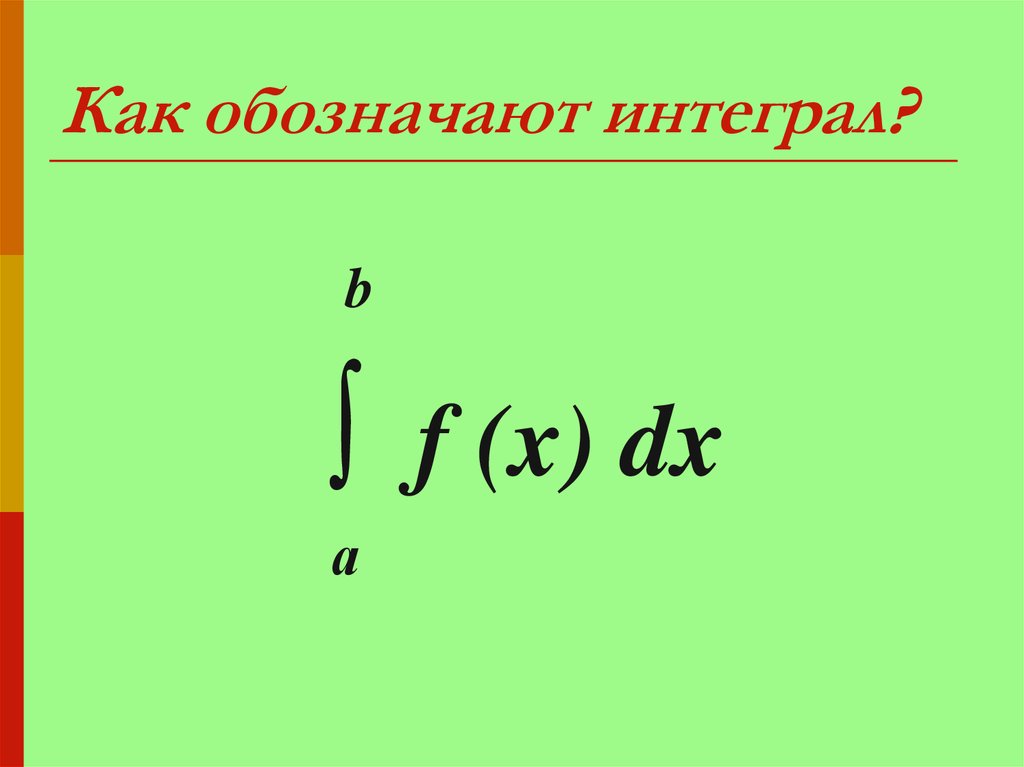







 Математика
Математика








