Квадратные уравнения (8 класс)

1. Квадратные уравнения (8 класс)

Если т ы услышишь, чт о кт о-т о не
любит мат емат ику, не верь.
Её нельзя не любит ь - её можно
только не знат ь.

2.

Цели:
1.Обобщение и систематизация знаний по
теме «Квадратные уравнения»
2.Развитие навыков критериального
оценивания.
3. Воспитание самостоятельности при
решении учебных задач
Форма урока:
Путешествие к вершинам знаний по теме
«Квадратные уравнения»

3.

Путешествие к
вершинам знаний….

4.

Маршрут путешествия:
Первая вершина - «Основа основ»
(отработка теоретической базы)
Вторая вершина – «Техника безопасности»
(устные упражнения)
Третья вершина – «Лучше гор могут быть
только горы» (самостоятельная работа по
выбранным критериям)
Четвёртая вершина – «Сияющая вершина, или
умный в гору не пойдёт, умный гору обойдёт»
(решение заданий повышенного уровня
сложности)

5.

6.

Квадратные
уравнения
умели решать
около 2000 лет
до н. э.
вавилоняне.

7.

ДИОФАНТ
‫ ‬В арифметике Диофанта
отсутствуют понятие
отрицательного числа и общие
методы решения квадратных
уравнений.
325 – 409 г.г. по Р. Х.
знаменитый
александрийский
математик.
‫ ‬При составлении уравнений
Диофант для упрощения
решения умело выбирает
неизвестные.

8.

Интересные способы решения
квадратных уравнений
встречаются в трудах индийского
ученого Бхаскары
(600 – около 680г.г.).
И арабского ученого
Ал – Хорезми
(780 – около 850г.г.)

9. Задача знаменитого индийского математика XII в. Бхаскары:

Обезьянок резвых стая
всласть поевши, развлекалась,
их в квадрате часть восьмая
на поляне забавлялась,
а двенадцать по лианам
стали прыгать, повисая.
Сколько ж было обезьянок,
ты скажи мне, в этой стае?

10. Французский математик Франсуа Виет (1540 – 1603).

Виет первым догадался обозначить
буквами не только неизвестные, но и
коэффициенты при них. Ведь используя
буквы можно было записывать формулы.
Это был огромный шаг вперёд. Недаром
Виета часто называют «отцом алгебры».
Недостатком алгебры Виета было то, что
он признавал только положительные
числа. Полученные Виетом системы
равенств, связывающие корни уравнения
с коэффициентами, теперь называют
теоремой Виета.
Домино

11.

Определение квадратного
уравнения
Квадратным уравнением
называется уравнение вида
ax bx c 0,
2
где коэффициенты a,b,c-любые
действительные числа, причем
a 0.

12. Определение корня

• Корнем квадратного уравнения
ax bx c 0
2
называют такое значение переменной х,
при котором квадратный трехчлен
2
ax bx c обращается в нуль;

13. Типы квадратных уравнений

• полные
b 0, c 0
• неполные
а)
b 0
б)
c 0
в) b 0; c 0

14. Из представленных формул выпишите те, по которым можно решать квадратные уравнения

D b 4ac
2
D 2R
b=2k
b D
b D
x1
; x2
2a
2a
k k ac
a
2
x1, 2
a=1 x1, 2 k k c
2
S=Vt
S = П R²

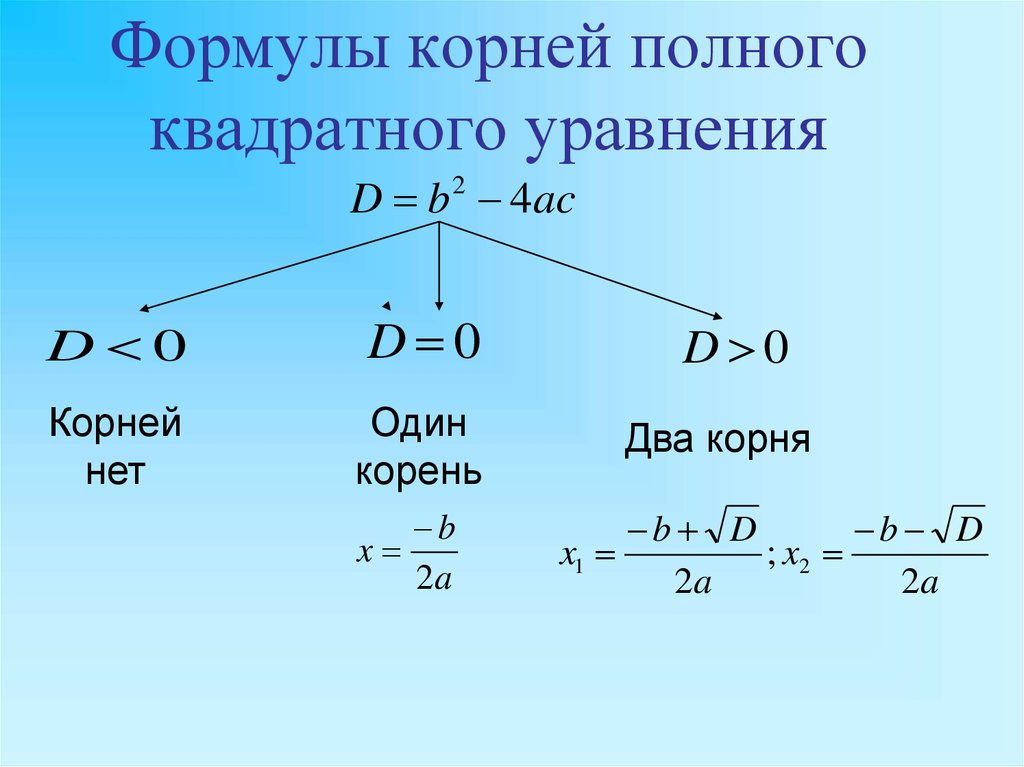
15. Формулы корней полного квадратного уравнения

D b 2 4ac
D 0
D 0
Корней
нет
Один
корень
b
x
2a
D 0
Два корня
b D
b D
x1
; x2
2a
2a

16. Формула четного коэффициента

b=2k
k k ac
a
a=1
2
x1, 2
x1, 2 k k c
2

17. Теорема Виета

x1 , x2
- корни квадратного уравнения
x1 x2
b
a
c
x1 x2
a
a 1
x1 x2 b; x1 x2 c
К маршруту

18. Вторая вершина – «Техника безопасности» (устные упражнения)

«Силу уму придают
упражнения, а не покой»
Александр Поуп –
английский поэт 18 века

19. Решите уравнения устно:

2
х –
3х=0
2
-х +9=0
2
х + 25 = 0
(х - 4) (х +2,7) = 0
2
7х =0

20. Найдите количество корней квадратного уравнения

х 5х 6 0
2
х 2х 6 0
2
х 12 х 36 0
2
К вершинам

21. Лучше гор могут быть только горы!

22. «Сияющая вершина, или умный в гору не пойдёт, умный гору обойдёт!»