Похожие презентации:
Геометрический смысл производной
1. Геометрический смысл производной.
Ромбах О.Б., преподаватель ГБПОУ «МИПКим.И.Федорова»
2.
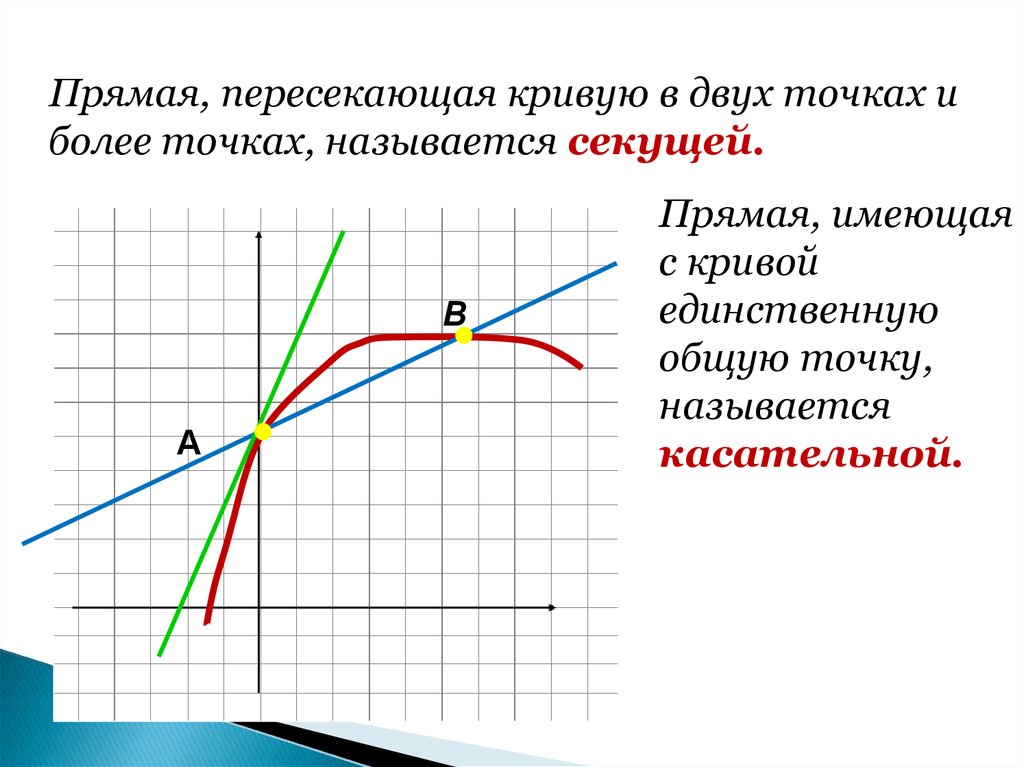
Прямая, пересекающая кривую в двух точках иболее точках, называется секущей.
В
А
Прямая, имеющая
с кривой
единственную
общую точку,
называется
касательной.
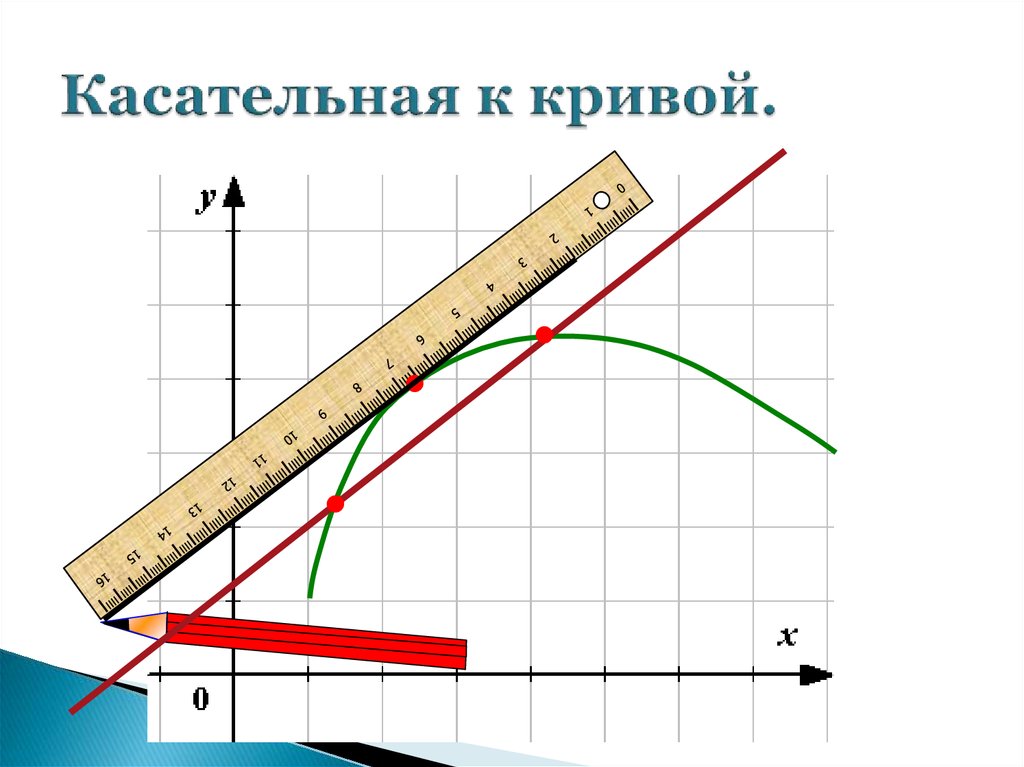
3. Касательная к кривой.
4.
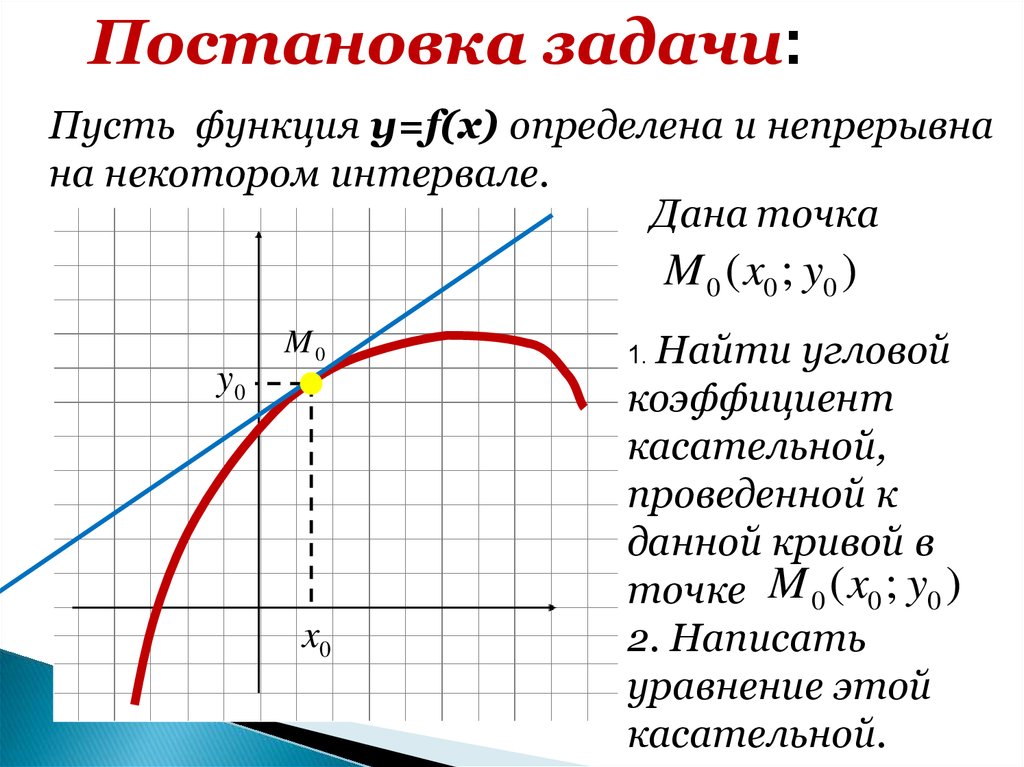
Постановка задачи:Пусть функция y=f(x) определена и непрерывна
на некотором интервале.
Дана точка
M 0 ( x0 ; y0 )
y0
M0
x0
1. Найти
угловой
коэффициент
касательной,
проведенной к
данной кривой в
точке M 0 ( x0 ; y0 )
2. Написать
уравнение этой
касательной.
5.
Проведем MM0секущую и найдемее угловой
коэффициент k,
зная координаты
точек M и M0
M 0 ( x0 ; y0 )
y
M
y
y
y0
y kx b
y y y0
y
tg
x
kсекущей tg
y f (x)
M0
x0
x
x x x0
x
k секущей
y
x
6.
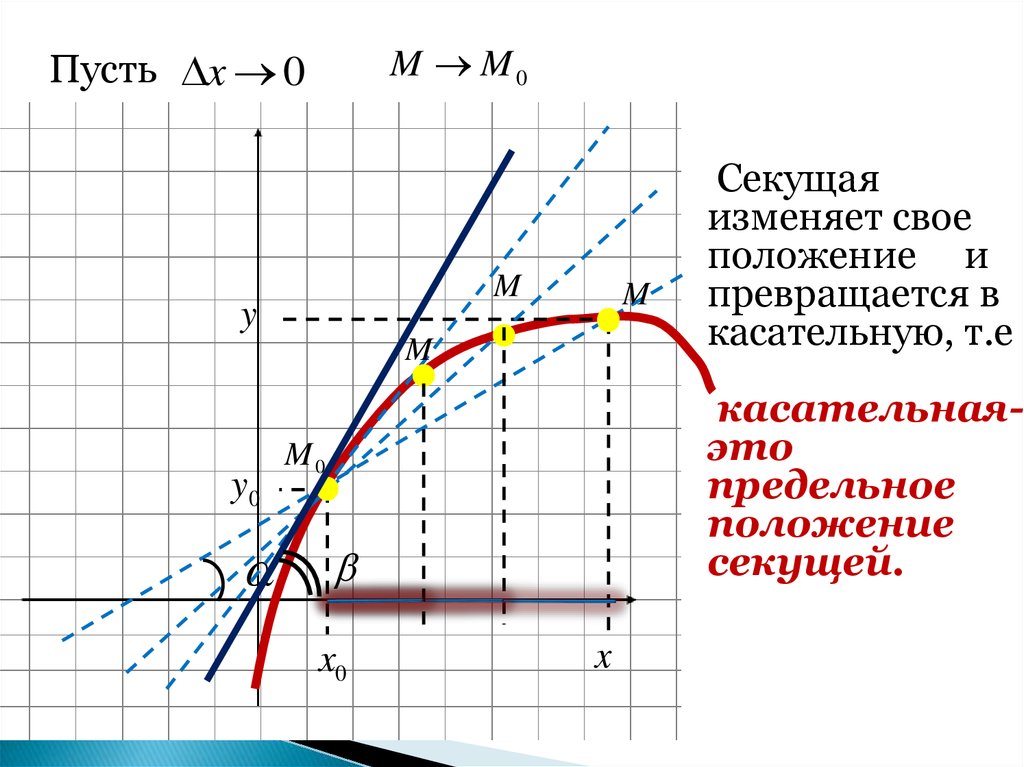
M M0Пусть x 0
M
y
M
M
y0
касательнаяэто
предельное
положение
секущей.
M0
x0
Секущая
изменяет свое
положение и
превращается в
касательную, т.е
x
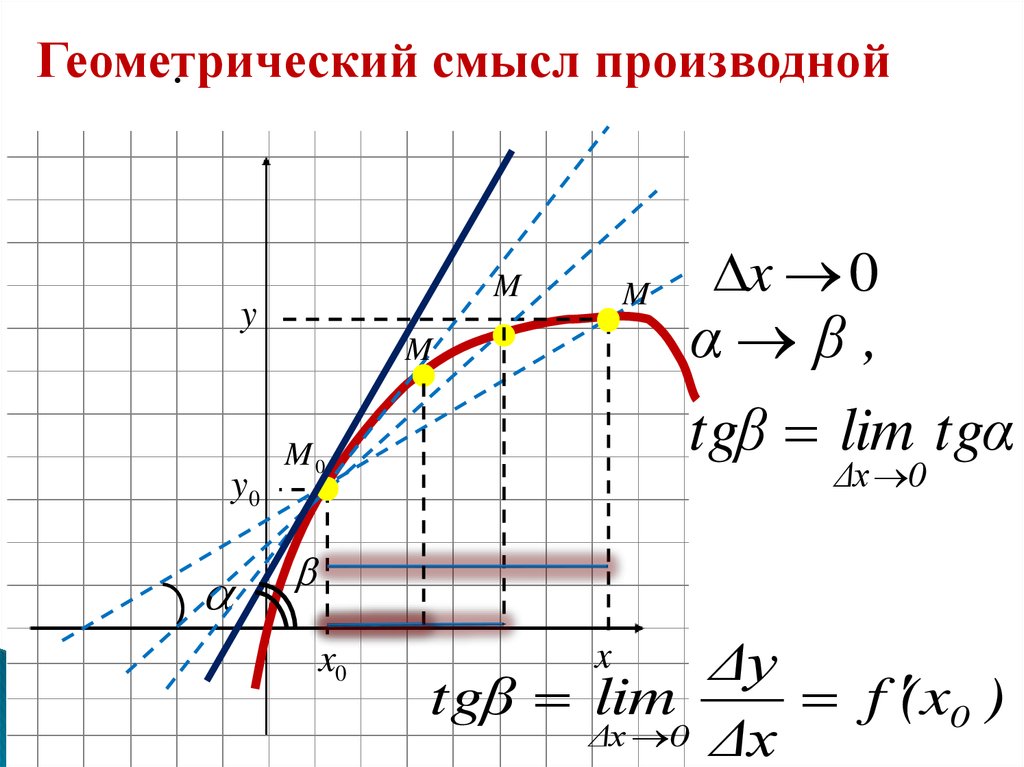
7.
Геометрическийсмысл производной
.
M
y
M
M
y0
x 0
α β,
tgβ lim tgα
M0
Δx 0
x0
Δy
tgβ lim
f (x0 )
Δx 0 Δx
x
8.
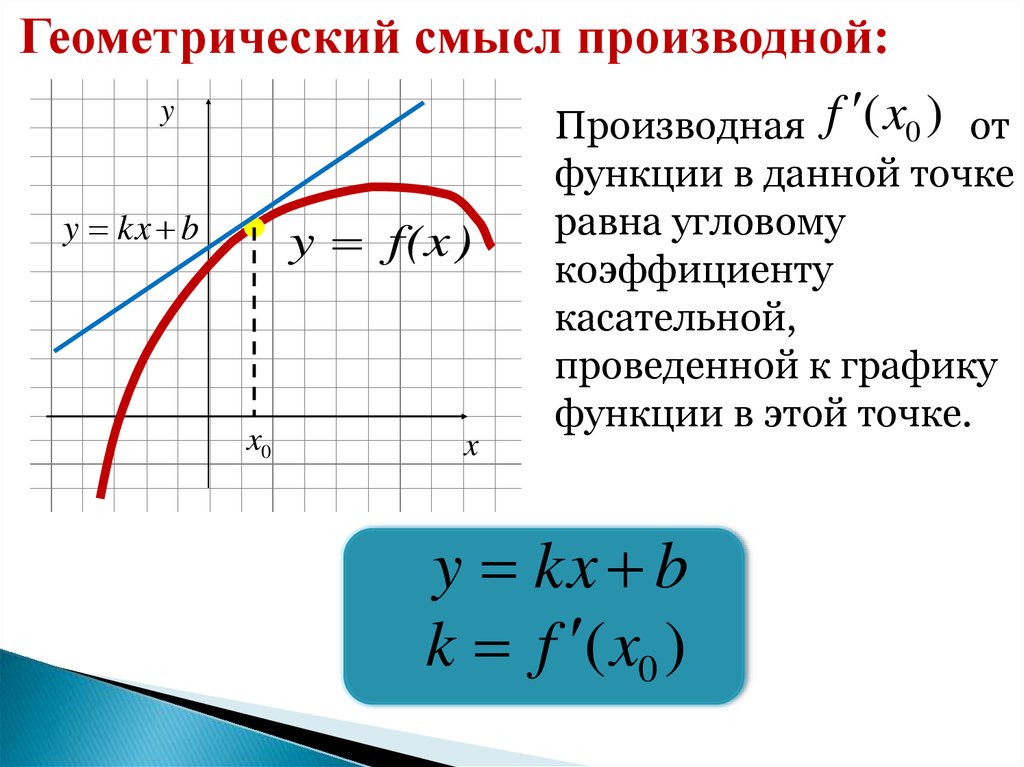
Геометрический смысл производной:y
Производная f ( x0 )
y kx b
y f(x)
x0
x
от
функции в данной точке
равна угловому
коэффициенту
касательной,
проведенной к графику
функции в этой точке.
y kx b
k f ( x0 )
9.
Геометрический смысл производной:«Если продолжить одно
из маленьких звеньев
ломаной, составляющей
кривую линию, то эта
продолженная таким
образом сторона будет
называться
касательной к кривой.»
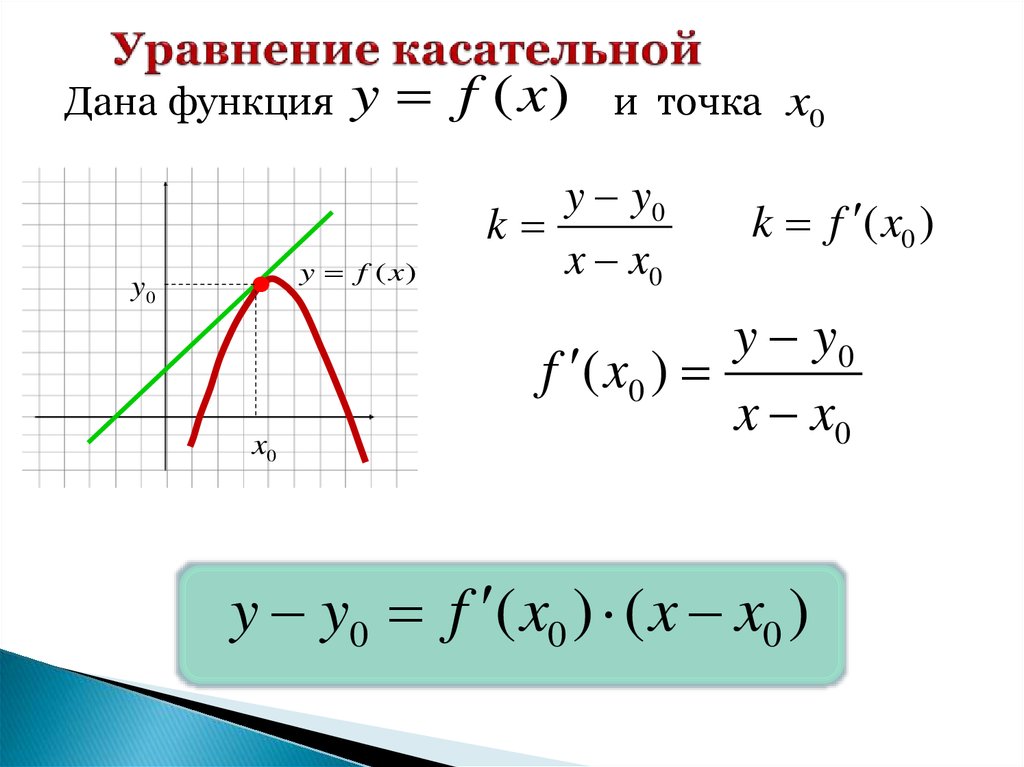
10. Уравнение касательной
Дана функцияy f (x)
y f (x)
y0
x0
и точка x0
y y0
k
x x0
k f ( x0 )
y y0
f ( x0 )
x x0
y y0 f ( x0 ) ( x x0 )



 Математика
Математика








