Понятие производной. Геометрический смысл производной

1. Тема: Понятие производной. Геометрический смысл производной.

2.

Вильгельм Лейбниц
(1646-1716)
Немецкий философ,
математик, физик,
языковед.мецкий философ,
мОдин из создателей
дифференциального и
интегрального исчислений.

3.

Исаак Ньютон (1643 – 1727)
Английский математик,
механик, астроном и
физик, создатель
классической механики.
Один из первых авторов
дифференциального и
интегрального
счисления.

4. Приращение функции и приращение аргумента

5.

приращение аргумента:
∆х = х – х0
y
Приращение функции :
∆f = f(x0 +∆x)-f(x0)
Yy=f(x)
f(x)=f(x0+∆x)
∆f = f(x)-f(x0)
∆f
f(x0)
x
x0
∆x
x=x0+∆x Т.е.,Дана
значение
функция
функции
f(x)
изменилось
на величину
Первоначальное
Пусть
В окрестности
х0- между
значение
Расстояние
точками
Функция
f(х)
тоже
примет
f(x)-f(x
0)= f(x
фиксированная
х00 +∆x)возьмём
получило
точка,
х иаргумента
х0точки
обозначим
∆х.Оно
новое
значение:
0+∆x)в
f(x
0),точку
КОТОРАЯ
НАЗЫВАЕТСЯ
приращение
f(х
0)- значение
х приращением
∆х,функци
иf(xновое
называется
ПРИРАЩЕНИЕМ ФУНКЦИИ И
значение
точке х0 и
х равно
равно х0+∆х
аргумента
ОБОЗНАЧАЕТСЯ ∆f
разности между х и х0:

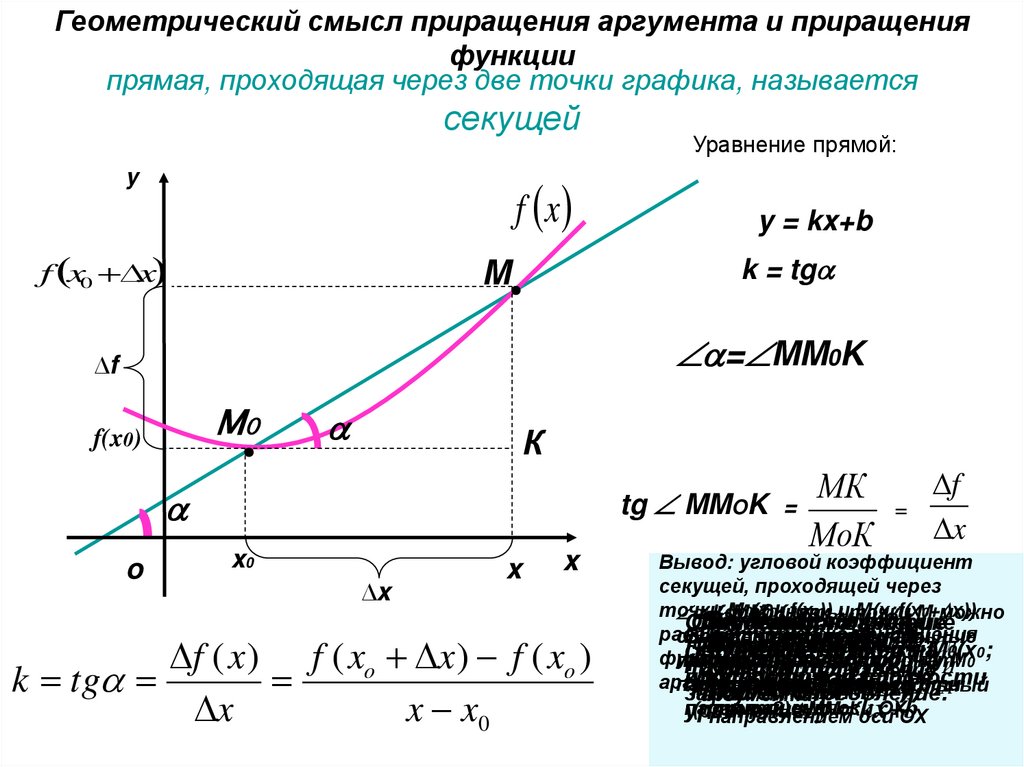
6. прямая, проходящая через две точки графика, называется секущей

Геометрический смысл приращения аргумента и приращения
функции
прямая, проходящая через две точки графика, называется
секущей
f x
y
f x0 x
Уравнение прямой:
y = kx+b
k = tg
M
= MM0K
∆f
M0
f(x0)
К
o
x0
∆x
x
x
f ( x ) f ( xo x ) f ( xo )
k tg
x
x x0
f
МК
tg MMOK =
=
x
МоК
Вывод: угловой коэффициент
секущей, проходящей через
точки
0(х00K
; f(х
0)) иточки
М(х;f(х
0+можно
х))
Координаты
М
Выразим
=Где
М
MM
,как
k- тангенс
tg
MM
угла,
0K
Определим
Секущая-прямая.
Отметим
положение
на
графике
ОПРЕДЕЛИМ
равен
отношению
приращения
соответственные
рассматривать
как
Выполним
дополнительные
Через
точки
М
иуглы
Мна
0
который
прямая
Отметим
этот
угол
ГЕОМЕТРИЧЕСКИЙ
СМЫСЛ
через
приращение
секущей
Положение
функции
на
f(x)
прямой
точки
М0(х0;
функции
к
приращению
при
приращение
секущейточку
координат
построения:
через
Отметим
К точку
ии ИМ0
проведём
прямую
ПРИРАЩЕНИЯ
ФУНКЦИИ
образует
с
функции
и
приращение
координатной
плоскости
задаёт
плоскости
её
аргумента
параллельных
точки
Мпрямую,
0 Отметим
прямых
проведём
рассмотрим
прямоугольный
ПРИРАЩЕНИЯ
АРГУМЕНТА
f(х
0)) и (записать)
М(х;f(х
0 + х эти
положительным
запишем
определение:
аргумента:
приращения
параллельную
оси
ОХОХ
(почему?)
∆ММ
0Кkx+b
уравнение
y=
направлением
оси
))

7. Определение

Производной функции y=f(x) называется
число, к которому стремится отношение
приращения функции к приращению
аргумента при x 0
f
f ( xo x ) f ( xo )
f ( x )
0
x
x x0

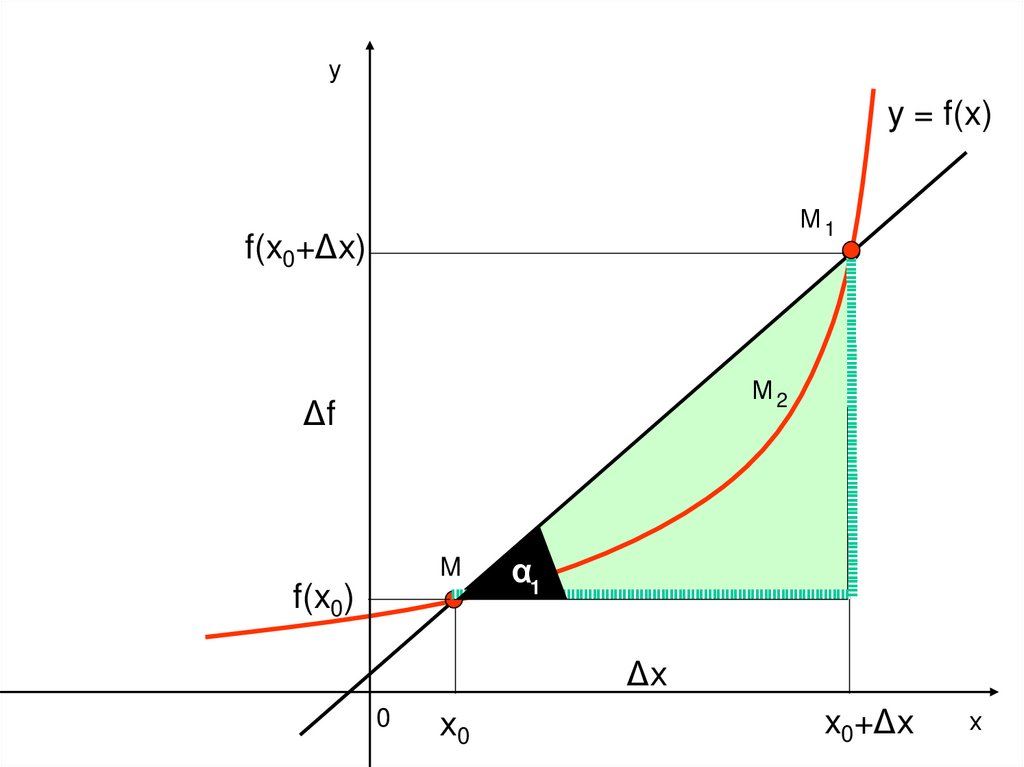
8. Геометрический смысл производной

9.

fу
k1 tg 1
x
y = f(x)
М1
f(x0+Δх)
Δf
M0
f(x0)
α1
Δх
0
х0
x0+Δх
х

10.

у
y = f(x)
М1
f(x0+Δх)
М2
Δf
M
f(x0)
α1
Δх
0
х0
x0+Δх
х

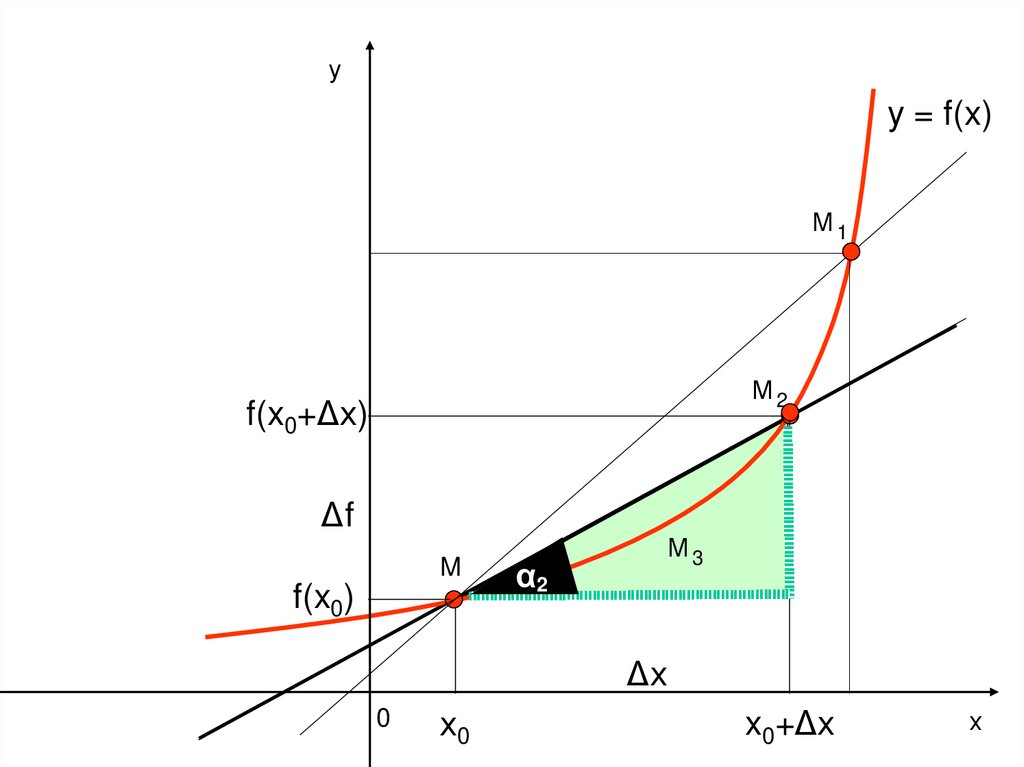
11.

f ( x0 у x) f ( x0 ) f
k 2 tg 2
x
x
y = f(x)
М1
М2
f(x0+Δх)
Δf
M0
f(x0)
α2
Δх
0
х0
x0+Δх
х

12.

у
y = f(x)
М1
М2
f(x0+Δх)
Δf
M
f(x0)
М3
α2
Δх
0
х0
x0+Δх
х

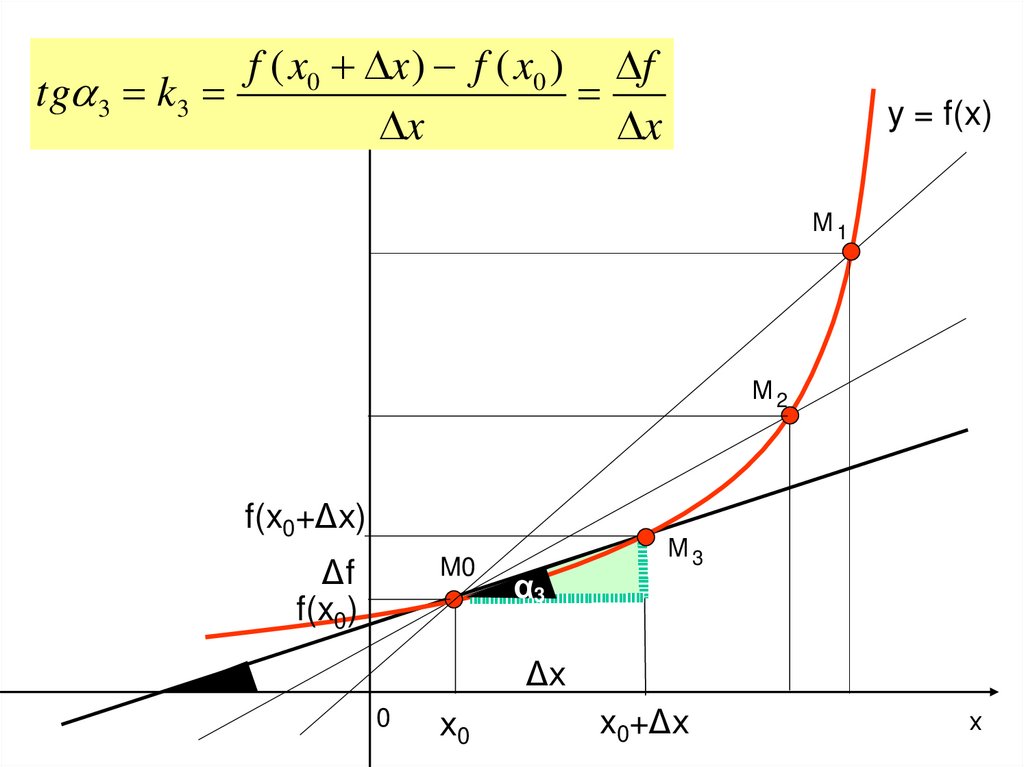
13.

f ( x0 у x ) f ( x0 ) f
tg 3 k3
x
x
y = f(x)
М1
М2
f(x0+Δх)
Δf
f(x0)
M0
α3
М3
Δх
0
х0
x0+Δх
х

14.

у
y = f(x)
М1
М2
f(x0+Δх)
Δf
f(x0)
M
α3
М3
Δх
0
х0
x0+Δх
х

15.

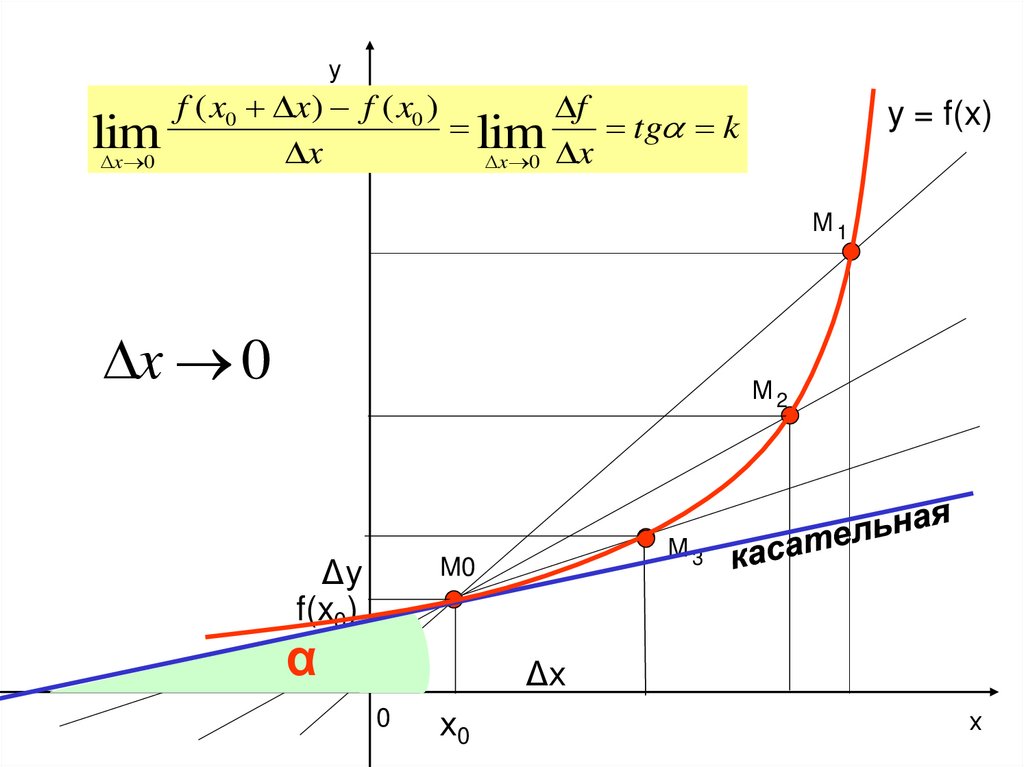
у
f ( x0 x ) f ( x0 )
f
lim
tg k
lim
x
x 0
x 0 x
y = f(x)
М1
x 0
М2
Δу
f(x0)
М3
M0
α
Δх
0
х0
х

16. Определение

Производной функции y=f(x) называется
предел отношения приращения функции
к приращению аргумента при x 0
f ( xo x) f ( xo )
f
( x0 )
lim
x
x 0
Производная функции f в точке x0 равна угловому
коэффициенту касательной, проведенной к графику
функции y=f(x) в точке M0(x0;f(x0)).
k tg f ( x 0 )