Похожие презентации:
Алгоритм построения графика квадратичной функции
1. Алгоритм построения графика квадратичной функции.
1.Определить направление ветвейпараболы.
2.Найти координаты вершины
параболы.
3.Провести ось симметирии.
4.Определить точки пересечения
графика с осью абсцисс.
5.Составить таблицу значений
функции с учётом оси симметрии.
2. Определение направления ветвей
a<0, то ветвипараболы направлены вниз, если
a>0, то вверх.
Если коэффициент
3. Координаты вершины параболы
Координатыформулам
Вершина:
вершины находятся по
4. Ось симметрии
Осьсимметрии параболы - это
вертикальная линия, уравнение
которой:
5. Определить точки пересечения с осью абсцисс
Нужно решить уравнение:Если решений нет, то и точек пересечения нет
если решение одно, то парабола соприкасается
с осью абсцисс своей вершиной
Если решений два, то мы получим 2 точки
пересечения, (где x1 и x2 – корни верхнего
уравнения):
и
6. Составить таблицу значений функции с учётом оси симметрии
1. Значения x выбираются симметричноотносительно точки
2. В таблицу значений должны попасть:
А) Вершина
Б) Нули (точки пересечения с осью
абсцисс)
В) Выбранные симметричные точки
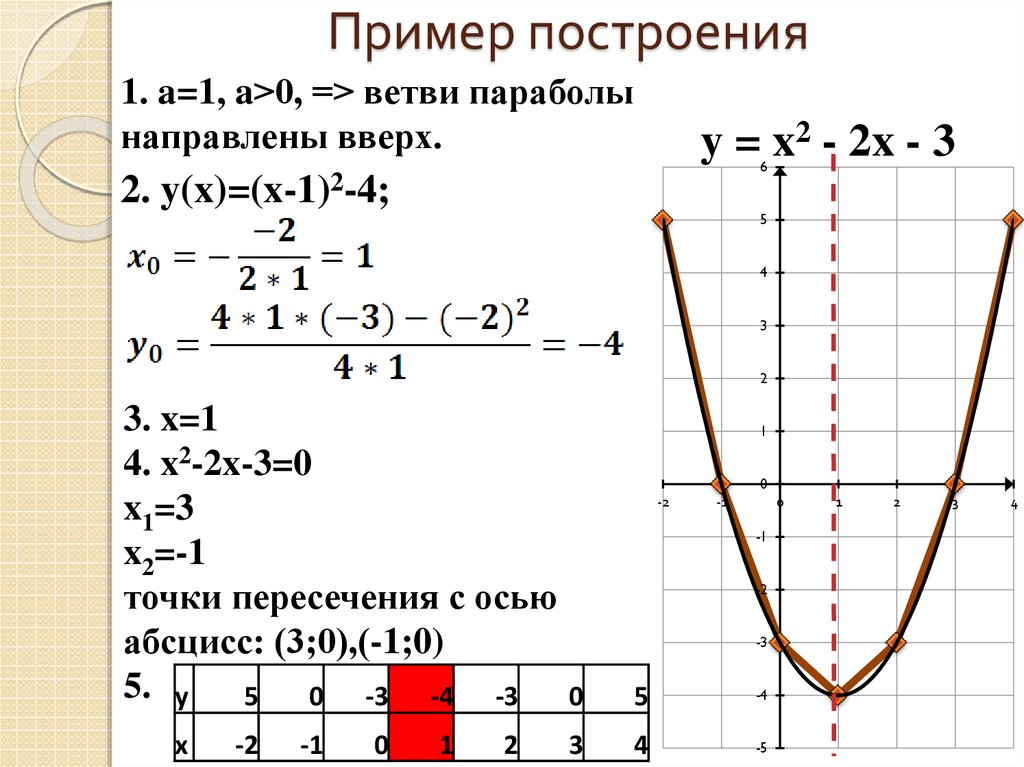
7. Пример построения
1. a=1, a>0, => ветви параболынаправлены вверх.
2.
y = x2 - 2x - 3
6
y(x)=(x-1)2-4;
5
4
3
2
3. x=1
4. x2-2x-3=0
x1=3
x2=-1
точки пересечения с осью
абсцисс: (3;0),(-1;0)
5. y 5 0 -3 -4 -3
x
-2
-1
0
1
2
1
0
-2
-1
0
-1
-2
-3
0
5
-4
3
4
-5
1
2
3
4






 Математика
Математика








