Похожие презентации:
Решение простейших тригонометрических уравнений с помощью единичной окружности
1.
Решение простейшихтригонометрических уравнений
с помощью единичной окружности
10
класс
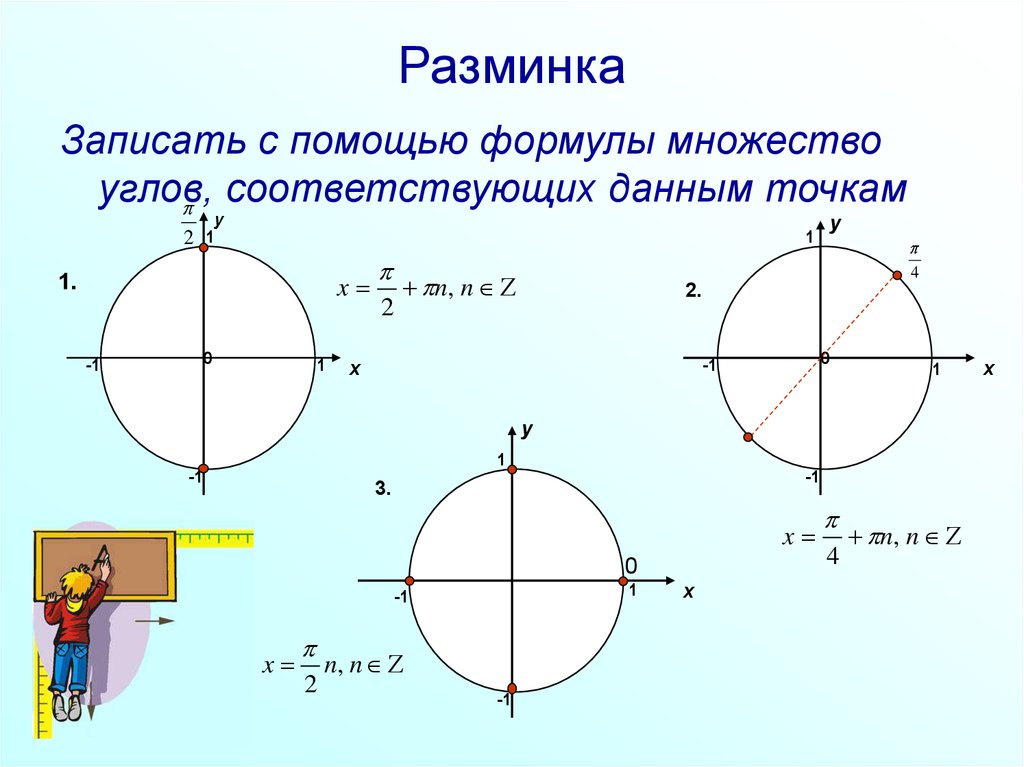
2. Разминка
Записать с помощью формулы множествоуглов,
соответствующих данным точкам
у
1
2
x
1.
-1
у
1
0
1
2
n, n
4
2.
х
0
-1
1
у
1
-1
-1
3.
x
0
1
-1
x
2
n, n
-1
х
4
n, n
х
3.
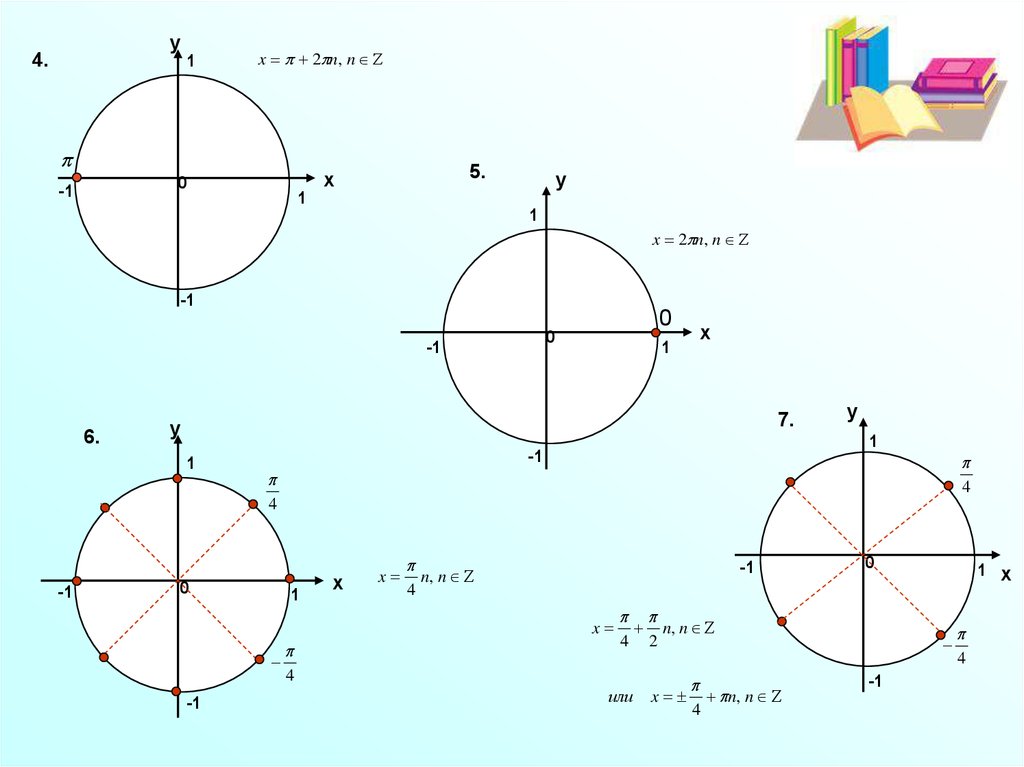
у4.
1
x 2 n, n
5.
х
0
-1
у
1
1
x 2 n, n
-1
0
0
-1
6.
х
1
7.
у
1
у
1
-1
4
4
-1
0
1
х
x
4
-1
n, n
x
-1
4
2
n, n
4
или
0
x
4
n, n
1 х
-1
4
4. Обратная задача: отметить точками углы, соответствующие данным формулам
у1.
1
x
2
1
2.
у
2 n, n
3
у
0
-1
х
1
2
3.
1
0
2
0
1
х
у
3
1
2
-1
0
1
-1
-1
1
-1
-1
-1
4.
-1
x
х
x
3
2 n, n
2
2
2
n, n
3
x
3
n, n
х
5. Решить уравнения
1.1
у (sinx)
1
2.
5
6
y (sinx)
1
2
6
0
0
-1
-1
sin x 0
x n, n
1
х (cosx)
0
-1
1
-1
1
sin x
2
x
2 n, n
6
x 5 2 n, n
6
x (cosx)
6.
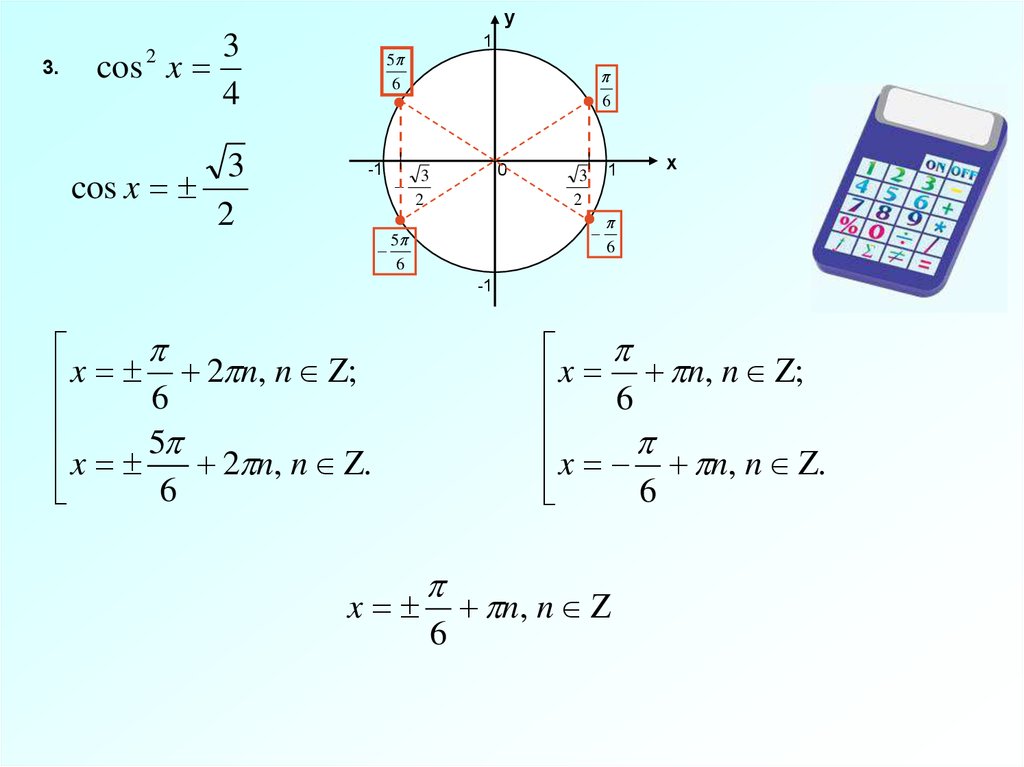
у3.
3
cos x
4
3
cos x
2
1
5
6
2
-1
6
0
3
2
1
3
2
5
6
х
6
-1
x 6 n, n ;
x n, n .
6
x 6 2 n, n ;
x 5 2 n, n .
6
x
6
n, n
7.
уtgx
1
tg x 1
2
1
4
3
4
tgx 1
x
4
2
n, n
0
1
0
-1
3
4
-1
4
-1
х
8.
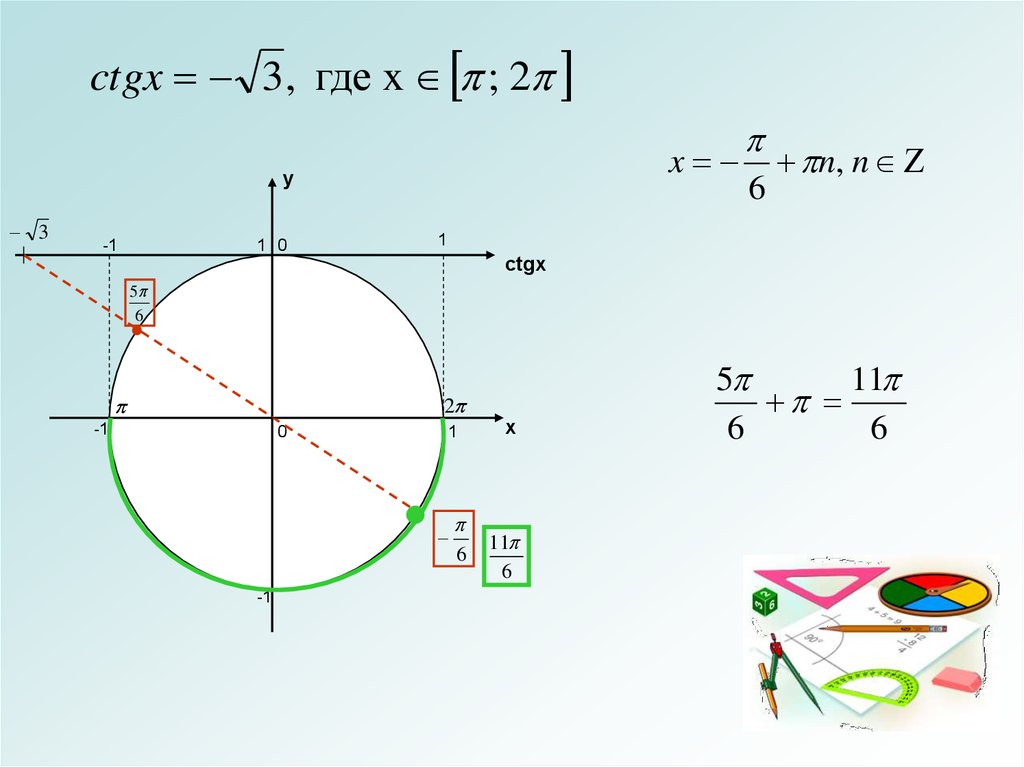
ctgx 3 , где x ; 2x
y
3
-1
1 0
6
n, n
1
ctgx
5
6
2
-1
0
1
-1
6
x
11
6
5
11
6
6
9. Аналитический способ отбора корней из промежутка
x n, n6
n 2 , n ;
7 6n 13, n ;
6
1
1 n 2, n ;
6
6 1 6n 12, n ;
1
1
1 n 2 , n ;
6
6
11
n 2; x 2
6
6
ОТВЕТ:
11
6
10.
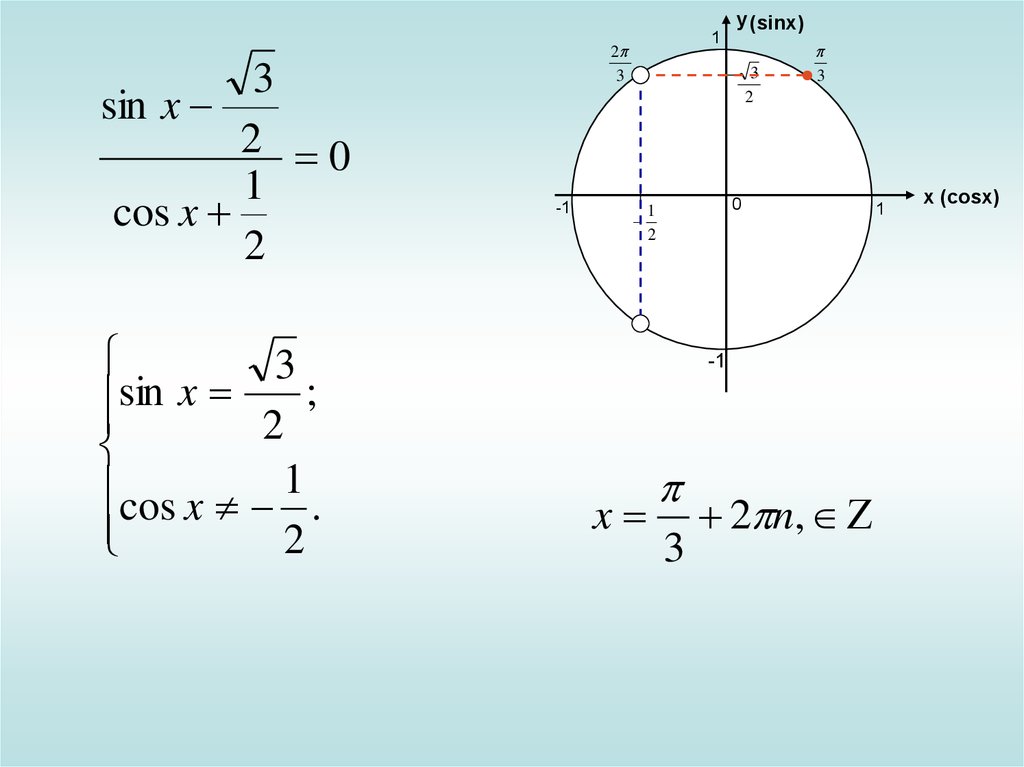
3sin x
2 0
1
cos x
2
3
;
sin x
2
cos x 1 .
2
1
2
3
-1
у (sinx)
3
2
3
0
1
2
-1
x
3
2 n,
1
х (cosx)
11.
При каких значениях параметра a уравнениеsin 2 x 2a 1 sin x a 2 a 0 имеет решение?
D 2a 1 4 1 a 2 a 4a 2 4a 1 4a 2 4a 1
2
sin x a 1;
sin x a.
2
0
1 a 1 1,
1 a 1;
0 a 2,
1 a 1.
-1
1
a 1; 2
a
a
12. Самостоятельная работа
ВАРИАНТ 1ВАРИАНТ2
Решите уравнения
cos x 0
sin x 1
1
sin x
2
ctgx 3
2
cos x
2
3
tgx
3
ctgx sin x 1
tgx cos x 1
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ
sin x
x2
0
cos x sin x 2 0
x 1; 3
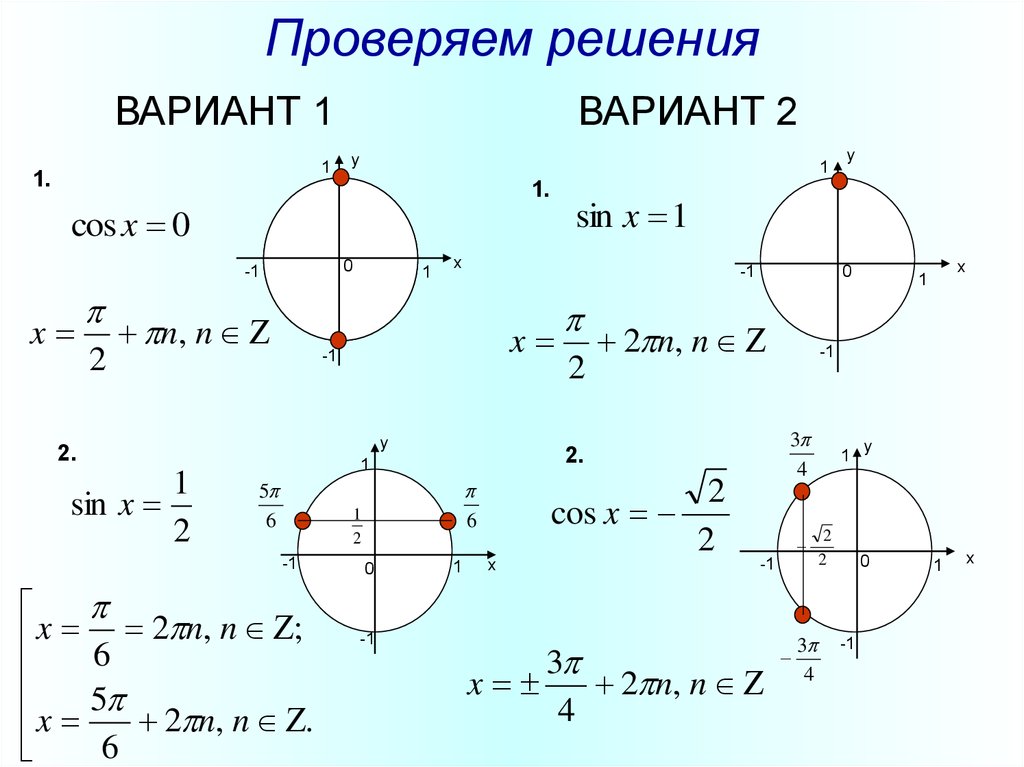
13. Проверяем решения
ВАРИАНТ 11
1.
ВАРИАНТ 2
y
1
1.
cos x 0
0
-1
x
2
n, n
-1
x
y
6
1
2
-1
x 6 2 n, n ;
x 5 2 n, n .
6
0
2
0
2 n, n
1
cos x
x
-1
x
2
2
-1
3
2 n, n
4
x
1
-1
3
4
2.
1
5
6
sin x 1
x
-1
2.
1
sin x
2
1
y
3
4
1
2
2
y
0
-1
1
x
14.
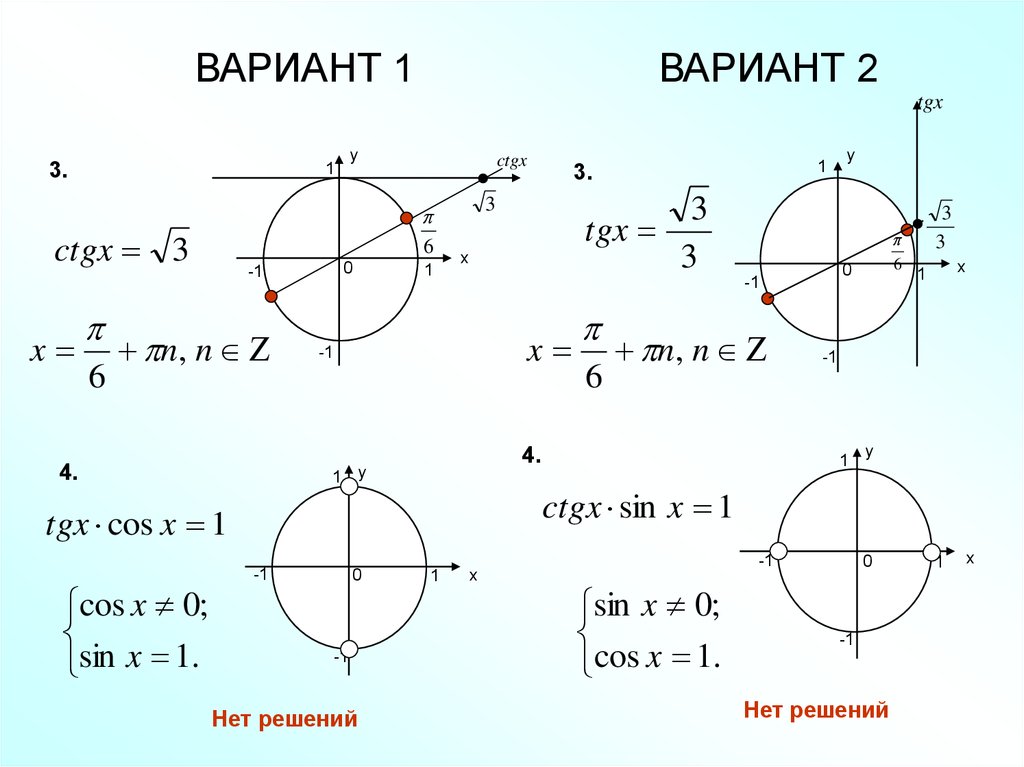
ВАРИАНТ 1ВАРИАНТ 2
tgx
3.
6
ctgx
6
ctgx 3
x
y
1
0
-1
n, n
4.
1
x
x
-1
Нет решений
6
n, n
4.
1 y
0
y
6
0
-1
3
3
x
1
-1
1
y
ctgx sin x 1
tgx cos x 1
cos x 0;
sin x 1.
3
tgx
3
3
-1
-1
1
3.
1
x
-1
sin x 0;
cos x 1.
0
-1
Нет решений
1
x
15. Домашняя работа
1. Дополнительные задания изсамостоятельной работы.
2. № 13.28, 13.29
3. При каких значениях
параметра
2
a
уравнение sin x a 2 имеет решения?
4.Найти наибольший отрицательный
2
cos
x 2 sin x 2 0.
корень уравнения



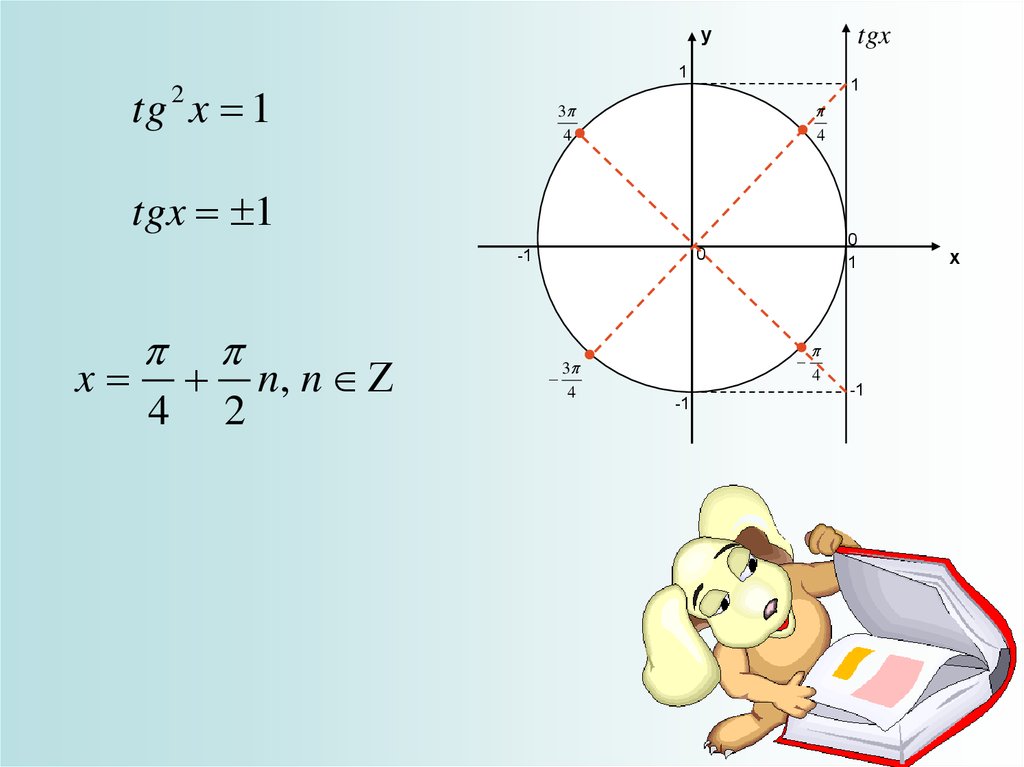





 Математика
Математика








