Дифференцирование. Производная функции в точке

1. Дифференцирование

Производная
функции в точке

2.

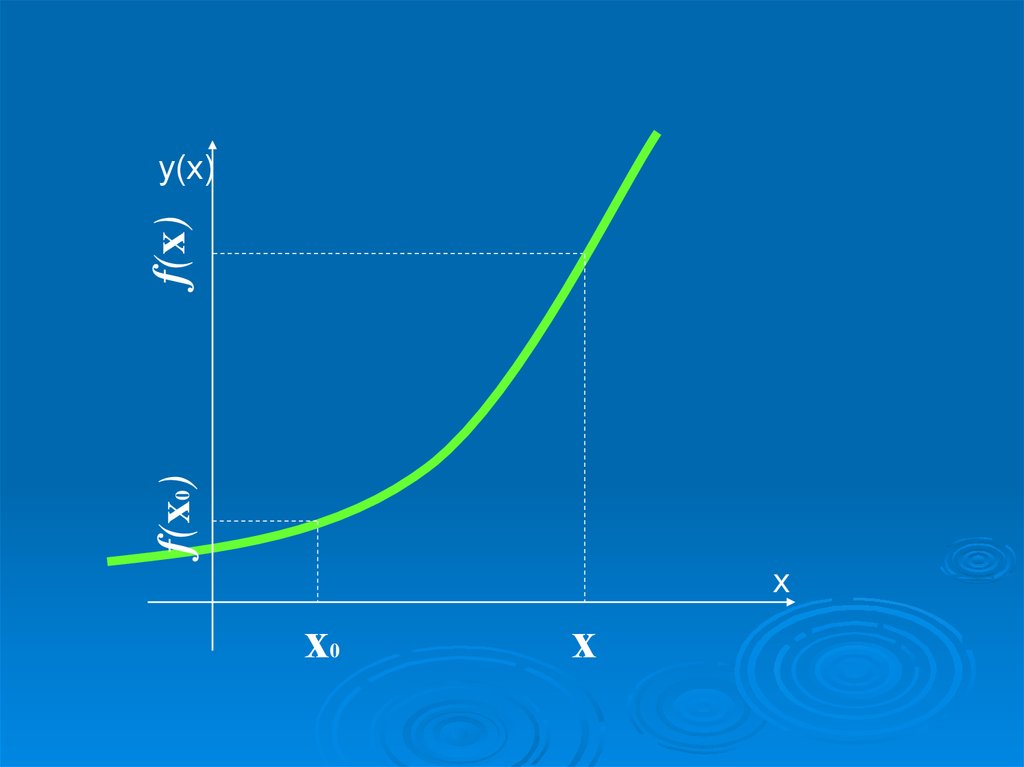
у(х)
х
х
0
х

3.

f(x0)
f(x)
у(х)
х
х
0
х

4.

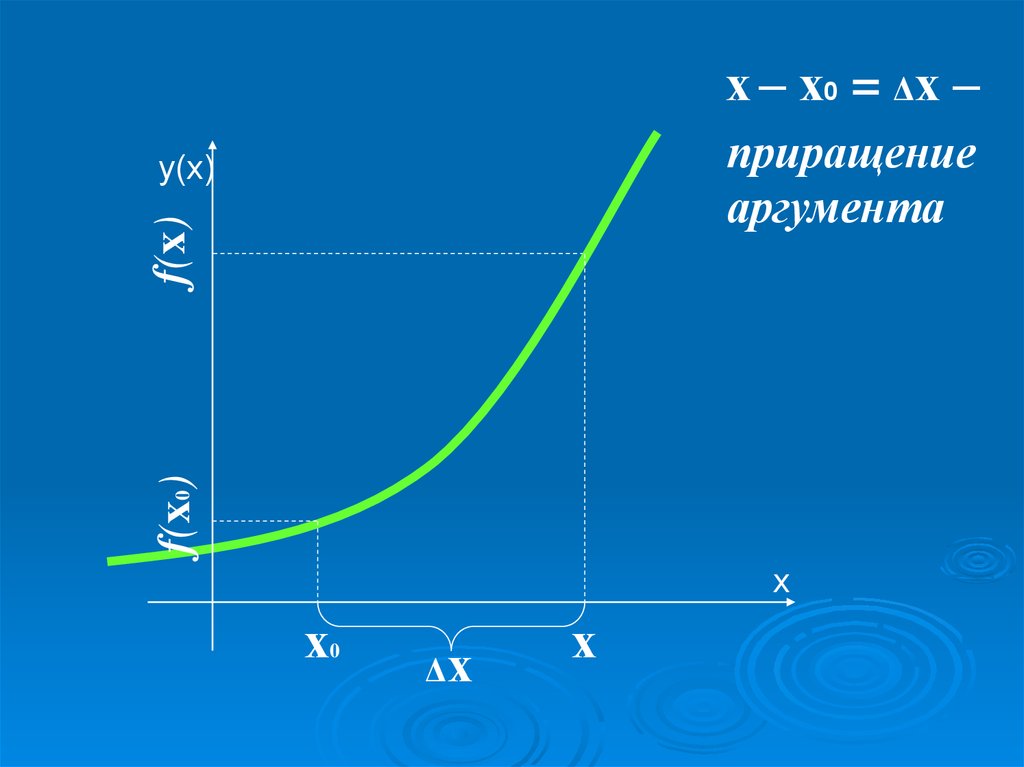
х – х0 = Δх –
приращение
аргумента
f(x0)
f(x)
у(х)
х
х
0
Δх
х

5.

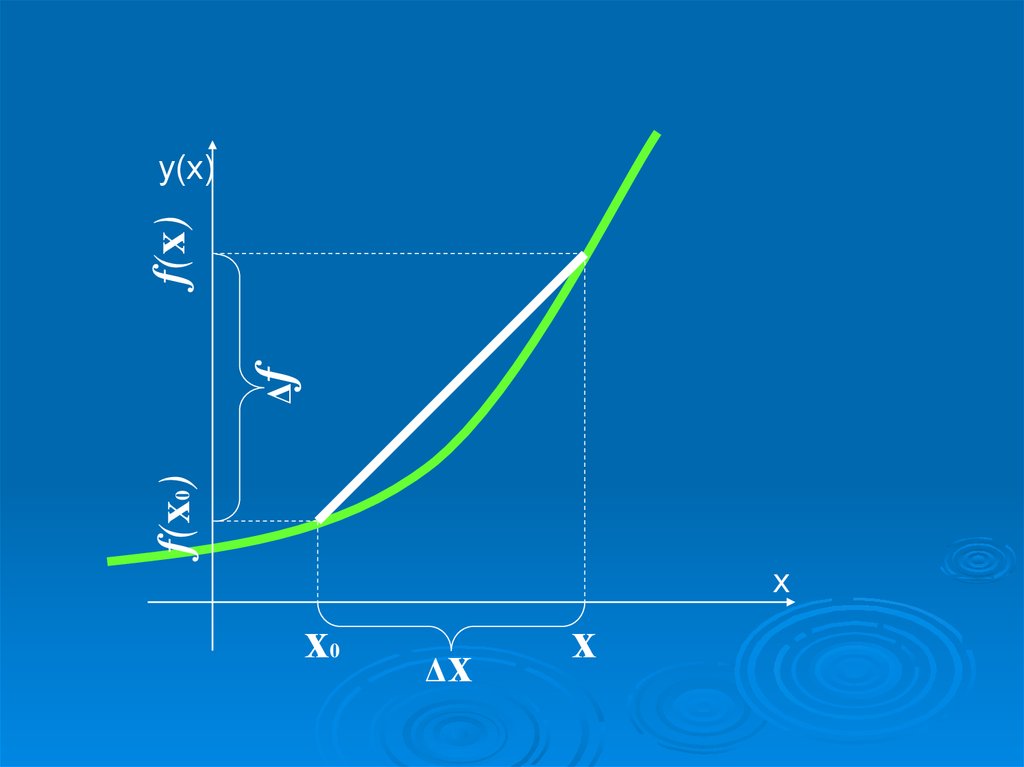
f(x0)
Δf
f(x)
у(х)
х
х
0
Δх
х

6.

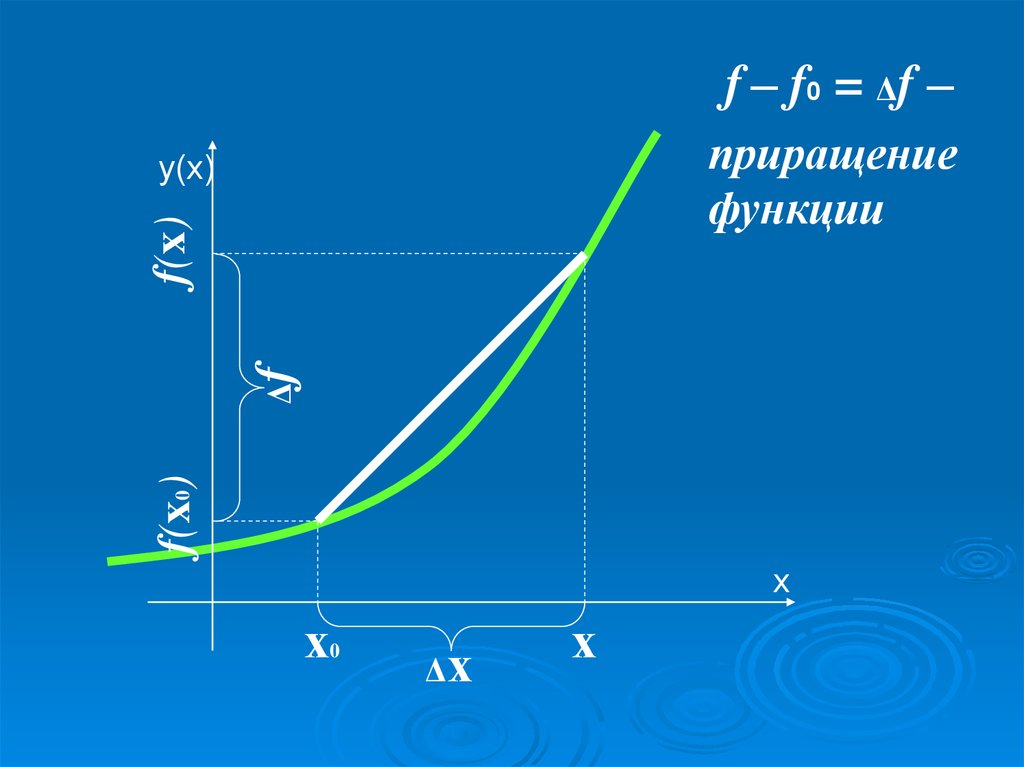
f – f0 = Δf –
приращение
функции
f(x0)
Δf
f(x)
у(х)
х
х
0
Δх
х

7.

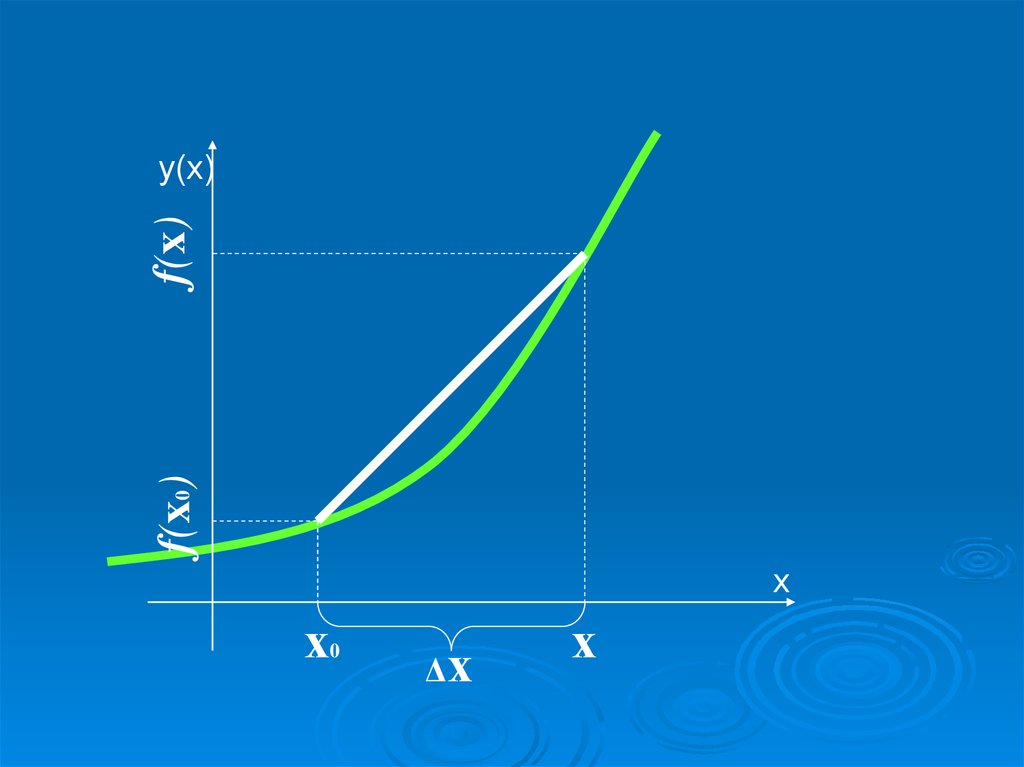
у(х)
f(x0)
f(x)
секущая
х
х
0
Δх
х

8.

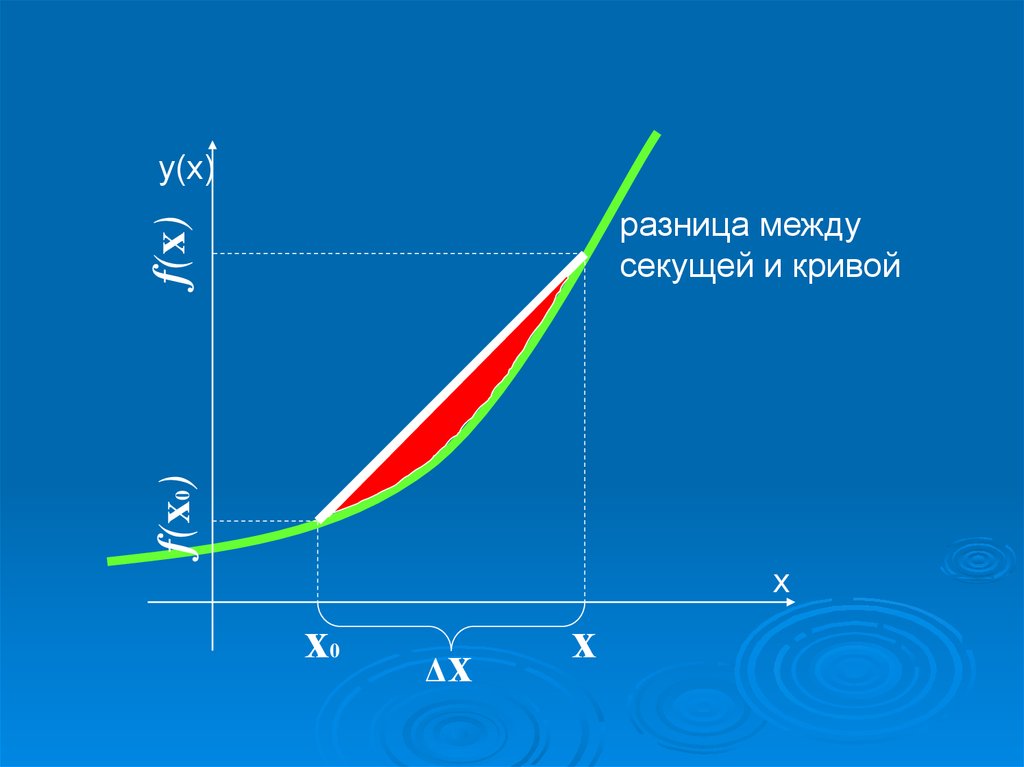
у(х)
f(x0)
f(x)
разница между
секущей и кривой
х
х
0
Δх
х

9.

f(x0)
f(x)
у(х)
х
х
0
Δх
х

10.

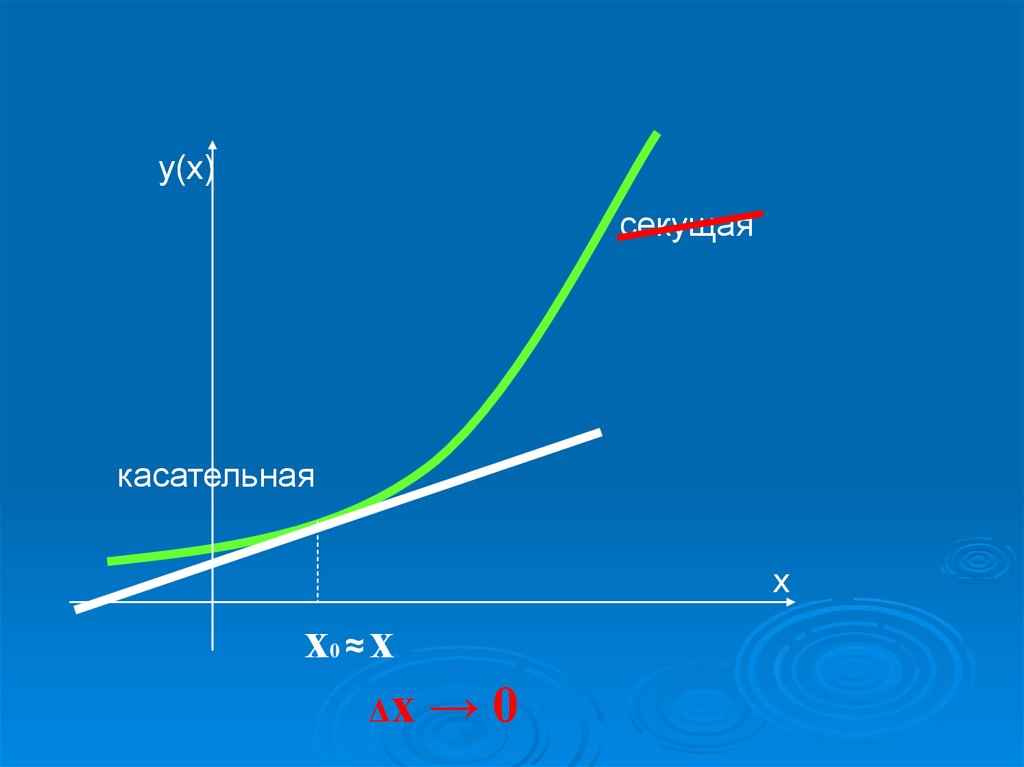
Замена секущей на касательную при Δх→0
называется предельным переходом
у(х)
f(x
≈ 0)
f(x)
секущая
х
х
0
х
≈
Δх
→0

11.

у(х)
секущая
касательная
х
х ≈х
Δх → 0
0

12. Выводы:

Кривые в каждой своей У прямых угол наклона
точке меняют угол
постоянный;
наклона;
Для построения кривой
Прямую можно
нужно знать
провести через две
бесконечное множество
различные точки;
точек;
Большинство графиков
Прямые хорошо
функций - кривые
изучены нами в теме
«Стереометрия»
Будем изучать кривые с помощью прямых
(касательных)

13. Связь между касательной и кривой (графиком функции)

График функции
Уравнение касательной
f f0
f (х)≠
x x0
Новая производная
функция
Предельный переход
при Δх→0:
f f0
f '(х)= lim
x 0 x x
0

14. Определение производной

Производной
функции f '(х) называется
предел отношения приращения
функции к приращению аргумента при
Δх→0
f f0
f lim
x 0 x x
0

15. Определение производной

Производной функции f '(х) называется
предел отношения приращения функции к
приращению аргумента при Δх→0
f f0
f lim
x 0 x x
0