Похожие презентации:
Мультимедийная разработка урока по алгебре. 10 класс
1. Муниципальное автономное общеобразовательное учреждение «Средняя общеобразовательная школа № 4»
Мультимедийнаяразработка урока
по алгебре 10 класс
Учитель математики
МАОУ СОШ № 4
Г. Покачи
Мухамедгалина Р.Р.
2. Тема урока: Два основных метода решения тригонометрических уравнений.
Тип урока: урок формирования новыхзнаний.
Форма урока: комбинированная.
Оборудование: мультимедиа-проектор,
презентация.
3.
Цели урока:образовательные:
повторение и расширение сведений учащихся о
тригонометрических уравнениях и способах их решения;
развивающие:
развитие умений самостоятельно приобретать новые знания и
использовать уже полученные для решения более сложных
задач;
воспитательные:
воспитание навыков самоконтроля и взаимоконтроля, умения
обобщать и систематизировать.
3
4.
План урока:I.
Организационная работа на уроке (5 мин.),
II. Актуализация опорных знаний (7 мин.),
III. Объяснение нового материала (10 мин.),
IV. Закрепление изученного материала (17 мин.),
V. Домашнее задание (3 мин.),
VI. Рефлексия, итог урока (3 мин.).
4
5.
Ход урока.I. Организационный момент.
1. Вступительное слово учителя.
2. Историческая справка, подготовленная
учащимся.
Цель этапа:
1) создание эмоционально-психологического
настроя на работу;
2) определить содержательные рамки урока;
3) познакомить с историей возникновения
тригонометрических уравнений.
5
6.
Историческая справкаТригонометрия, как и любая научная
дисциплина,
возникла
из
потребностей
практической деятельности человека. Различные
задачи астрономии, мореплавания, землемерия,
архитектуры привели к необходимости разработки
способа вычисления элементов геометрических
фигур, по известным значениям других их
элементов, найденных путем непосредственных
измерений.
Само название «тригонометрия» греческого
происхождения,
обозначающее
«измерение
треугольников»: (тригонон) – треугольник,
(метрейн) – измерение.
Одним из основоположников тригонометрии
считается древнегреческий астроном Гиппарх,
живший во II веке до н.э. Гиппарх является
автором первых тригонометрических таблиц.
Гиппарх Никейский,
предполагаемый автор
первых
тригонометрических
таблиц
7.
Историческая справкаРазвитию аналитической теории тригонометрических функций
содействовали И. Ньютон и Л. Эйлер. Основоположником этой теории
следует считать Л. Эйлера. Он придал всей тригонометрии
современный вид. Дальнейшее развитие теории было положено в XIX в.
Н. И. Лобачевским и другими учёными.
Тригонометрические уравнения возникают при решении задач по
планиметрии, стереометрии, астрономии, физики и в других областях.
Еще древнегреческие математики, используя элементы тригонометрии
для решения прямоугольных треугольников, фактически составляли и
решали простейшие тригонометрические уравнения. Исторически
учение о решении тригонометрических уравнений формировалось с
развитием теории тригонометрических функций, а также черпало из
алгебры общие методы их решения. Часть тригонометрических
уравнений непосредственно решается сведением их к простейшему
виду, иногда – с предварительным разложением левой части уравнения
на множители, когда правая часть равна нулю. В некоторых случаях
удается произвести замену неизвестных таким образом, что
тригонометрическое уравнение преобразуется в «удобное» для решения
алгебраическое уравнение.
8.
II. Актуализация опорных знаний.Теоретический опрос (устный).
Цель этапа:
1) уточнение основных понятий, коррекция
знаний по изученной ранее теме «Решение
простейших тригонометрических
уравнений»;
2) развитие внимания, памяти;
3) развитие умений математически грамотно
выражать свою мысль.
8
9.
Теоретический опрос• С какими функциями вы познакомились на
прошлом уроке?
• Назовите аналитические и графические модели
данных функций.
•В каких реальных ситуациях нашли применение
данные функции?
•Перечислите основные свойства функций.
•Какие виды задач вы умеете решать?
9
10. На какие вопросы надо уметь отвечать при изучении функции:
• Имя функции• Модели
(аналитическая и
графическая)
• Реальные ситуации,
которые могут быть
описаны с помощью
этой функции
• Свойства функции
• Типы задач
• Тригонометрические
• y=cosx, y=sinx, y=tgx, y=ctgx
Косинусоида, синусоида,
тангенсоида, котангенсоида
• Гармонические колебания
• Область определения,
периодичность, четностьнечетность, промежутки
возрастания (убывания),
ограниченность, наименьшее и
наибольшее значения,
непрерывность, множество
значений
• Построить график функции,
прочитать график функции,
решить уравнение, решить
неравенство
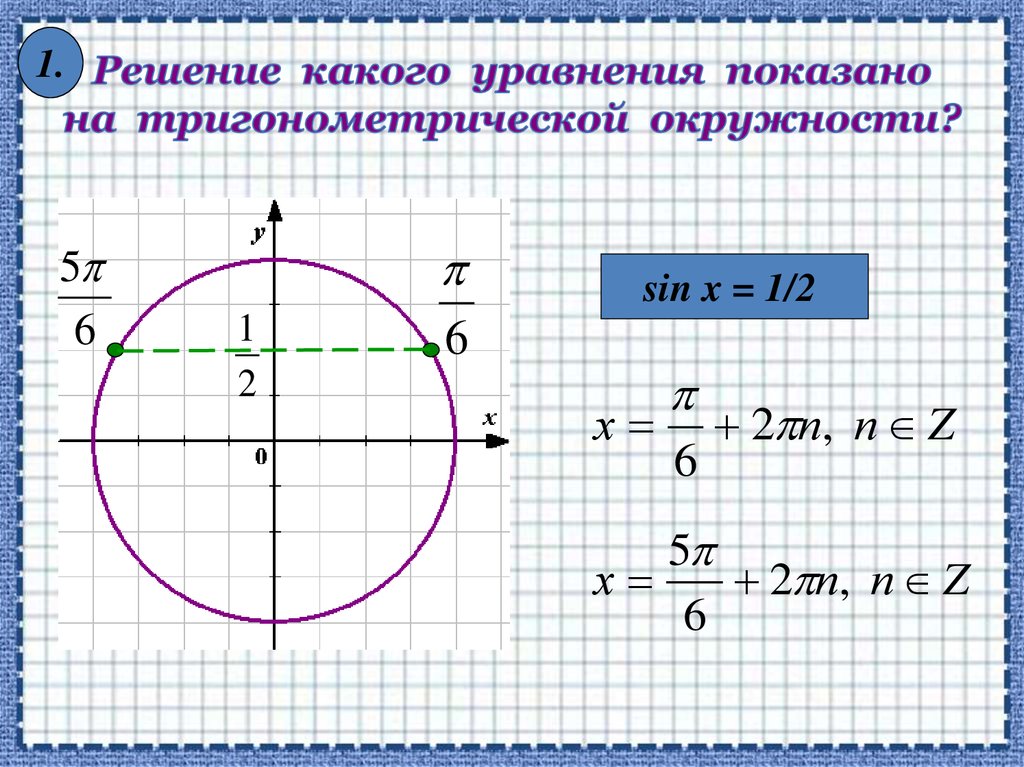
11. Решение какого уравнения показано на тригонометрической окружности?
1.5
6
1
2
6
sin x = 1/2
х
6
2 п, п Z
5
х
2 п, п Z
6
12. Решение какого уравнения показано на тригонометрической окружности?
2.4
cos x = √2/2
х
2
2
4
х
4
4
2 п, п Z
2 п, п Z
13. Решение какого уравнения показано на тригонометрической окружности?
3.tg x = -√3/3
х
6
3
3
6
п, п Z
14. Решение какого уравнения показано на тригонометрической окружности?
4.6
3
ctg x = √3
х
6
п, п Z
15.
Проблема…sint=-2
cost=0,7
sint=-0,3
Решение данной
проблемы – это задача
на следующий урок!
16.
III. Изучение нового материала.Цель этапа:
1) выделить новые типы уравнений, которые
можно решить на основе имеющихся знаний и
указать способы их решения (попытаться свести
к ранее известным алгебраическим уравнениям);
2) способствовать формированию применять
приемы: сравнения, обобщения, выявления
главного, переноса знаний в новую ситуацию,
развитию математического кругозора, мышления
и речи, внимания и памяти.
16
17. На какие вопросы надо уметь отвечать при изучении нового вида уравнения:
Что называется таким уравнением (его вид)?
Что называется корнем (решением) уравнения?
Что значит решить уравнение?
Способы решения.
18. Разбейте уравнения на группы, объединив по каким-либо признакам:
1.2.
3.
4.
5.
6.
7.
1
;
32
4х=
х2= ;
4
х(1-х)=0;
2х2+3х-2=0;
2х- 3=0;
(2х- 2)(х+1)=0;
|x-1|=1;
cos2x=
3
4
8.
;
9. |cost-1|=1;
10. 2cosх- 3=0;
11. 2sin2t+3sint-2=0;
1
12. sin4х= 2 ;
13. (2sint- 2)(cost+1)=0;
14. tgx(1-sinx)=0;
15. cos2x-sin2x-cosx=0.
19. По каким признакам вы объединили уравнения?
1 вариант:линейные: 1; 5
квадратные: 2; 4
рациональные: 3; 6
с модулем: 7; 9
тригонометрические: 815
2 вариант:
линейность: 1 и 12; 5 и
10;
квадратичность: 2 и 8;
4 и 11; 15
рациональность: 3 и 14;
6 и 13
модуль: 7 и 9
20. Метод введения новой переменной.
Необходимо произвести замену неизвестных таким образом,чтобы тригонометрическое уравнение преобразовалось в
«удобное» для решения алгебраическое уравнение.
Пример: решить уравнение 2sin2 + 3sin —2 = 0.
Это уравнение является квадратным относительно sinx.
Его корни: sinx =1/2 , sinx = -2. Второе из полученных
простейших уравнений не имеет решений, так как
|sinx|<=1, решения первого можно записать так: x=π/6+2πk,
x=5 π/6+2πk, k€Z.
21. Метод разложения на множители.
Под разложением на множители понимаетсяпредставление данного выражения в виде
произведения нескольких множителей. Если в
одной части уравнения стоит несколько
множителей, а в другой – 0, то каждый множитель
приравнивается к нулю. Таким образом, данный
множитель можно представить в виде совокупности
более простых уравнений.
22.
Пример: 2 sin3 x - cos 2x - sin x = 0Сгруппируем первый член с третьим, а
cos 2x = cos2 x - sin2 x.
(2sin3 x - sin x) – (cos2 x - sin2 x) = 0,
Вынесем из выражения, стоящего в первой скобке
sin x, а cos2 x = 1 - sin2 x.
sin x (2sin2 x – 1) – (1 - 2 sin2 x) = 0,
sin x (2sin2 x – 1) + (2 sin2 x - 1) = 0,
(2 sin2 x - 1) • ( sin x + 1) = 0.
2 sin2 x – 1 = 0
или
sin x + 1 = 0
sin2 x = 1/2,
sin x = - 1
Ответ: x1=± π/4+ πk, x2 = - π/2 +2πk, k € Z.
23. Вывод: решение произвольного тригонометрического уравнения, как правило, сводится к решению одного или нескольких простейших
24. IV. Закрепление материала.
Цель этапа:решение тригонометрических уравнений
методом введения новой переменной, методом
разложения на множители, сведением
уравнения к квадратному.
25. Работа по группам: решите уравнения
1 группа: линейные №10, №12;2 группа: рациональные №13, №14;
3 группа: квадратичные №8, №11, №15.
Фронтальная работа: уравнение с модулем
№9.
26. Закрепление изученного материала проводится в форме самостоятельного решения уравнений с взаимопроверкой.
1 вариант:1) sin2 x - sin x = 0, 2) 3 cos x + 2 sin 2x = 0,
3) 4 cos2 x +9 cos x +5=0;
2 вариант:
1) ctg2 x - 4 ctg x = 0, 2) 5 sin 2x - 2 sin x = 0,
3) sin(π/2+x)+ cos x=1.
27. Домашнее задание
1 группа – № 18.1(а), 18.6(а), 18.11(а),2 группа – № 18.2(а), 18.7(б), 18.21(а),
3 группа – №18.2(б), 18.8(а), 18.21(в).
28.
VI. Итог урока, рефлексия.Цель этапа:
1) зафиксировать новое содержание, изученное на уроке;
2) оценить собственную деятельность на уроке.
1.
2.
3.
4.
5.
6.
Ответить на вопросы учителя:
Какую задачу мы поставили перед собой сегодня на уроке?
Достигли мы этой цели?
Какие типы тригонометрических уравнений мы можем решать?
Какими способами мы это сделали, с помощью каких приёмов?
Каждое ли тригонометрическое уравнений мы теперь можем
решить? (Проблема!)
Какова задача на следующие уроки?
28
29. Рефлексия.
Оцените собственную деятельность на уроке:1) Какое значение для вас имеют знания и умения,
полученные на уроке? (Очень важны, важны, не
очень важны).
2) Как вы оцениваете полученные сегодня знания?
(Глубокие, осознанные, неосознанные).
3) Как вы оцениваете свою деятельность?
(Отлично, хорошо, удовлетворительно).





























 Математика
Математика Педагогика
Педагогика








