Похожие презентации:
Формулы корней квадратных уравнений
1. Проверка д/з
№ 25.14а) 1 8
б)
2 6
2
№ 25.31
х 8 2 ( х 4) 2 х 2
в) 3 6
г) 5 20
5
2. Тема урока: Формулы корней квадратных уравнений.
Цель урока: обобщить и систематизировать основные знания иумения по теме квадратные уравнения;
закрепить умения решать квадратные уравнения по формулам.
3.
«Для разысканияистины вещей
необходим метод»
Рене Декарт
(французский математик)
4. Полезно знать:
Исторические сведения:Квадратные уравнения впервые встречаются в работе
индийского математика и астронома Ариабхатты.
Другой индийский ученый Брахмагупта (VII в) изложил
общее правило решения квадратных уравнений, которое
практически совпадает с современным.
В Древней Индии были распространены публичные
соревнования в решении трудных задач. Задачи часто
облекались в стихотворную форму.
________________________________________________
Вот задача Бхаскары:
Обезьянок резвых стая, всласть поевши, развлекалась.
Их в квадрате часть восьмая на полянке забавлялась.
А двенадцать по лианам стали прыгать, повисая.
Сколько ж было обезьянок, ты скажи мне, в этой стае?
5. Устная работа
Для того чтобы включиться в работу и сконцентрироватьсяпредлагаю вам небольшую устную разминку.
1. Какое название имеет уравнение второй степени?
2. От чего зависит количество корней квадратного уравнения?
4. Сколько корней имеет квадратное уравнение, если дискриминант больше 0?
5. Что значит решить уравнение?
6. Как называется квадратное уравнение, у которого коэффициент а равен 1?
7. Сколько корней имеет квадратное уравнение, если дискриминант меньше 0?
6.
КВАДРАТНЫЕ УРАВНЕНИЯПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
а ≠ 0, в ≠ 0,
ах2+вх+с=0
НЕПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
с ≠ 0
а ≠ 0, в = 0, с = 0
ах2+вх=0
ах2+с=о
ах2=0
7.
РЕШЕНИЕНЕПОЛНЫХ
КВАДРАТНЫХ УРАВНЕНИЙ
в=0
с=0
в,с=0
ах2+с=0
ах2+вх=0
ах2=0
1.Перенос с в правую част ь
уравнения.
1.
ах2= -с
х(ах + в) = 0
2.Деление обеих част ей
уравнения на а.
2.
3.Если –с/а>0 -два решения:
с
а
и х2 = -
Разбиение уравнения
на два равносильных:
х2= -с/а
х1 =
Вынесение х за
скобки:
Если –с/а<0 - нет решений
с
а
х=0
или
ах + в = 0
3. Два решения:
х = 0 и х = -в/а
1.Деление обеих част ей
уравнения на а
х2 = 0
2.Одно решение: х = 0.
8. Тест ( 2мин) взаимопроверка
õ2Тест ( 2мин)
взаимопроверка
а) х2 +6 х + 3 = 0
а) – х +х2 + 4 = 0
б)
б) 8 + 5х2 = 0
2 х2 + 9 = 0
в) -7 + х2 = 0
в) -х + х2 = 0
г) х – 5х2 +1= 0
г) - х2 +12х + 7 = 0
д) - х + 12х2 +8= 0
д) - х + 11х2 = 15
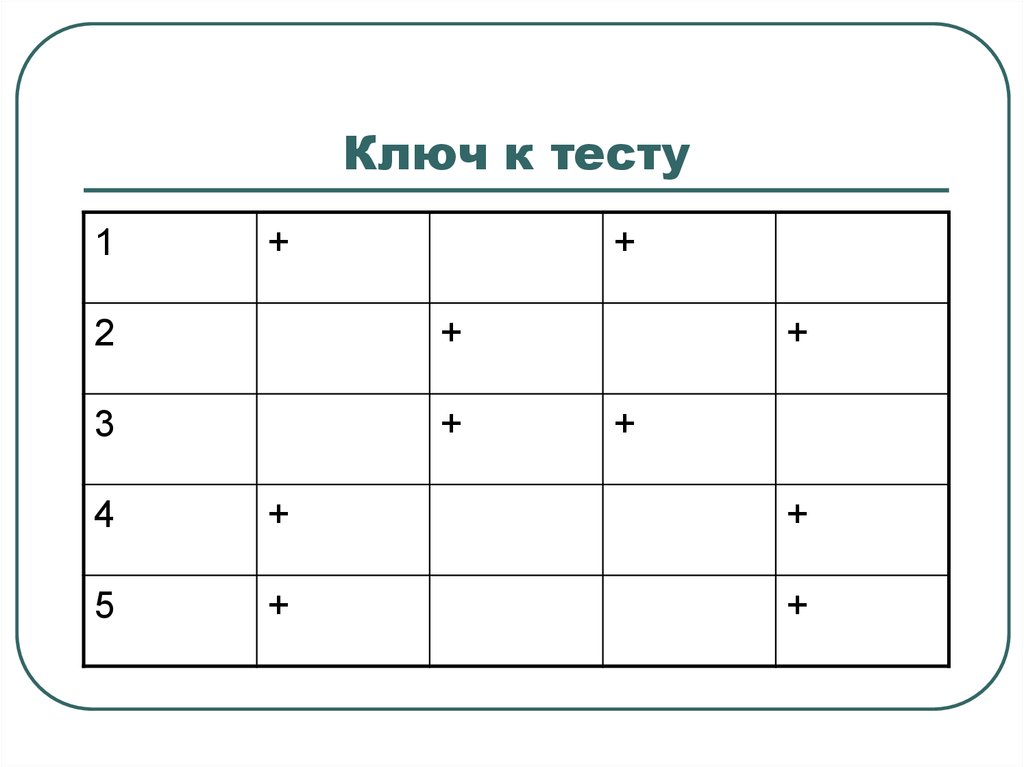
9. Ключ к тесту
1+
+
2
+
3
+
+
+
4
+
+
5
+
+
10.
А теперь, ребята , расскажите алгоритмрешения полного квадратного уравнения.
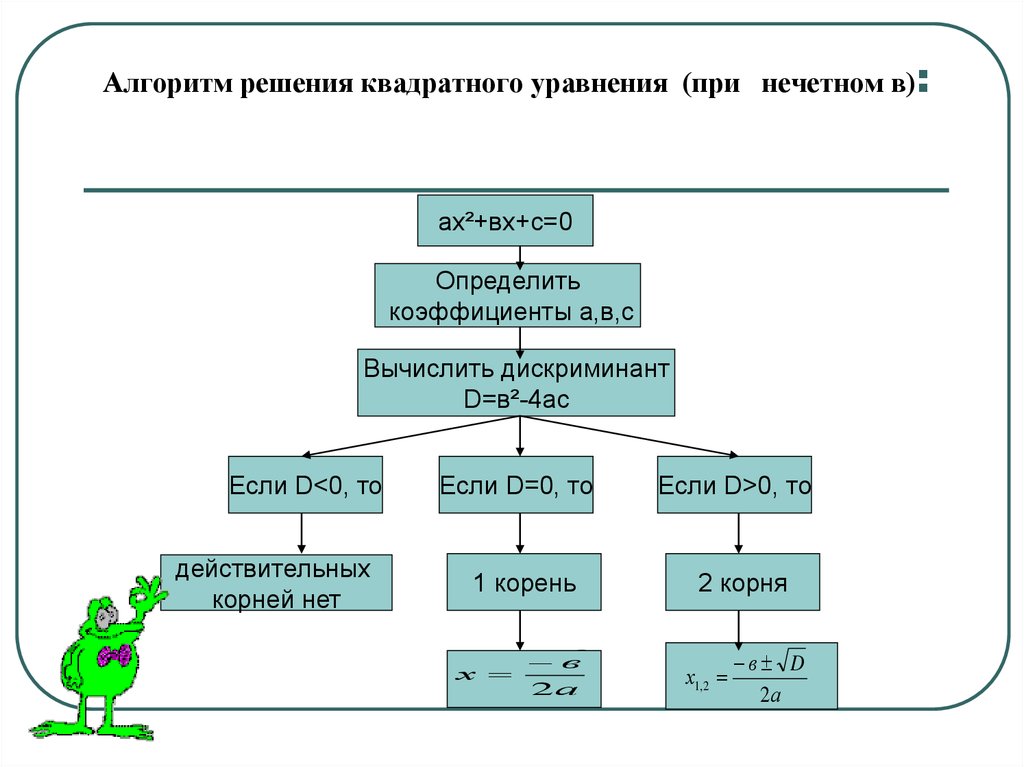
11. Алгоритм решения квадратного уравнения (при нечетном в):
ах²+вх+с=0Определить
коэффициенты а,в,с
Вычислить дискриминант
D=в²-4ас
Если D<0, то
действительных
корней нет
Если D=0, то
1 корень
х
х
в
2а
в
2а
Если D>0, то
2 корня
х1, 2
х1, 2
вв D
D
2а
2а
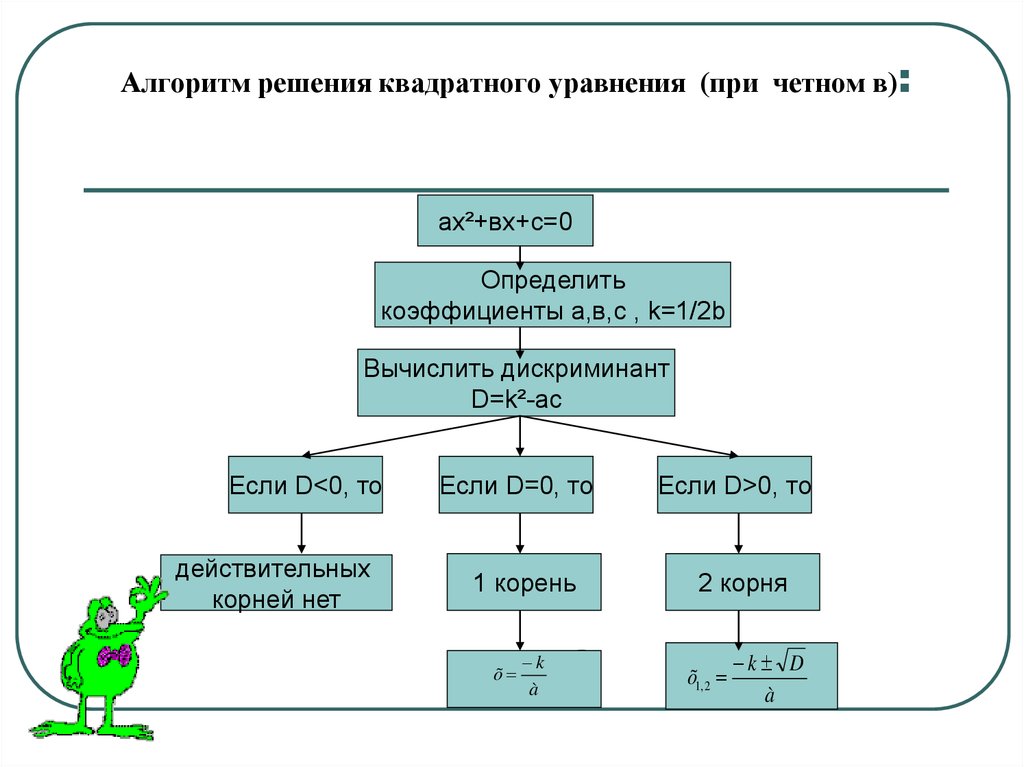
12. Алгоритм решения квадратного уравнения (при четном в):
ах²+вх+с=0Определить
коэффициенты а,в,с , k=1/2b
Вычислить дискриминант
D=k²-ас
Если D<0, то
действительных
корней нет
Если D=0, то
1 корень
k в
õ
х
à
2а
Если D>0, то
2 корня
х1, 2
õ1, 2
вk D
D
2а
à
13.
14. Актуализация знаний
1. x2 – 7х +6 = 02. x2 + х – 2 = 0
1. 8х2 -6 х +1=0
2. 3х2 – 2х + 5 = 0
1.
2.
3. 2х2+ х -3=0
3. х2 – 4х +3 = 0
3
1.Найдите сторону квадрата, площадь которого равна 81 см2.
2.Найдите стороны прямоугольника, длина которого на 4 см больше ширины, а площадь
равна 60 см2
3. Произведение двух последовательных натуральных чисел больше их суммы на 109.
Найдите эти числа.
4.Обезьянок резвых стая, всласть поевши, развлекалась.
Их в квадрате часть восьмая на полянке забавлялась.
А двенадцать по лианам стали прыгать, повисая.
Сколько ж было обезьянок, ты скажи мне, в этой стае?
15. Повторение.
Соотнесите функцию с графиком16.
РефлексияМогу решать уравнения
самостоятельно
Нужна помощь
при решении уравнений
Совсем не могу
решать уравнения
17. Домашнее задание
Итог урокаобобщили и систематизировали основные знания и умения по теме
квадратные уравнения ;
закрепили умения решать квадратные уравнения по формулам.
Домашнее задание
П. 25
№25.4 (ОРО)
№ 25.37(а,б),
№ 25.43















 Математика
Математика








