Поиск рациональных методов решения (8 класс с углубленным изучением математики)

1. Поиск рациональных методов решения

8 класс с углубленным изучением математики
Учитель математики МОУ СОШ № 32
г. Энгельса Саратовской обл.
Фифнер Е.П.

2. Проект

Вид проекта:
исследовательский.
Форма проекта: презентация.
Цель:
а) повторение и систематизация знаний по
пройденным темам;
б) поиск рациональных решений;
в) включение обучающихся в проектную
деятельность;
г) оптимизация учебного процесса через
организацию самостоятельной деятельности

3. Задачи

а) Повысить уровень интеллектуальных
способностей за счёт использования
дополнительной информации, поиска
«нового».
б) Научить выделять главное.
в) Развивать навыки самостоятельной работы.
г) Научить анализировать, проводить
исследовательскую работу, работать сообща.
д) Научить выбирать рациональное решение.

4. Как реализовать проект

1.
2.
3.
4.
5.
6.
7.
8.
9.
Изучение ситуации.
Выделить главное.
Поиск методов решений.
Поиск необходимого теоретического
материала.
Исследовательская работа.
Экспертиза.
Реализация проекта.
Результат.
Выбор формы проекта.

5. Блок-схема проектирования

Озарение
Оформление идеи
Реальный проект
Экспертиза
Форма проекта,
демонстрация
Реализация

6. Задание

Найдите корни уравнения
,
если одним из его действительных корней
является положительный корень уравнения
Сравните значения действительных
корней исходного уравнения, удовлетворяющих неравенству
.
со значением выражения
План решения
Рациональные методы

7. I. План решения

1.
Решение уравнения
2.
Выбор положительного корня.
3.
Подставив его в уравнение (2), найти параметр a.
(1).
(2).
4.
5.
6.
7.
Решение уравнения (2).
Отбор действительных корней уравнения (2).
Решение неравенства
(3).
Отбор корней , удовлетворяющих неравенству (3).
Упрощение выражения
(4).
Сравнение значений действительных корней со
значением выражения (4).
Задание
Рациональные методы

8. II. Теоретический материал

1.
2.
3.
4.
5.
6.
7.
8.
Решение дробно-рациональных уравнений.
Графический способ решения уравнений.
Решение уравнений, используя подбор корней.
Разложение многочлена на множители.
Деление многочлена на многочлен.
Схема Горнера.
Комплексные и действительные числа.
Решение неравенств, содержащих знак модуля.
9.
Формула двойного радикала
10. Выделение квадрата двучлена.
11. Формула
12. Сравнение действительных чисел с
иррациональными.
.

9. 1) Решение уравнения

(1)
(1).
A. Графический способ.
B. Подбор корней.
C. Решение дробно-рационального
уравнения:
а) деление многочлена на многочлен;
б) схема Горнера.
План решения

10. А. Графический способ

a)
y
4
3; x 2.
x 2
График функции
y
4
3;
x 2
4
y
,x 0
получен из графика функции
x
В результате сдвига на 2 ед. отрезка влево вдоль оси Ox и на
3 ед. отрезка вверх вдоль оси Oy.
b) y=x2 . Квадратичная функция, график парабола
Графики пересекаются в точке,
с абсциссой 2.
Ответ: 2.

11. В. Подбор корней

X=2.
Проверка:
4
2
3 2 ;
2 2
4=4 - верно.
Ответ: 2 - корень уравнения.

12. C. Решение дробно-рационального уравнения.

а) Деление многочлена на многочлен.
4
3
x 2
x
2
( x 2).
ОДЗ: x≠-2
4+3(х+2)=х2(х+2),
4+3х+6=х3+2х,
х3+2х2-3х-10=0,
10: {10;-10;5;-5;2;-2;1;-1}. x=2,
(x-2) (x2+4x +5)=0
(x-2)=0 или x2+4x+5=0,
Х=2,
D=42-4×5=-4;
х3+2х2-3х-10
х3-2х2
4x2- 3х
4x2- 8х
удов. ОДЗ
D<0, действ. корней нет
5х-10
4 4 4 4 1 4 2i
x
2 i.
5х-10
2
2
2
1
x
Ответ:
2
4 4 4 4 1 4 2i
2 i.
2
2
2
2; 2 i; 2 i.
0
х-2
x2+4x +5

13.

б) Схема Горнера.
х3+2х2-3х-10=0, х=2 – действительный корень
уравнения.
х3
х2 х св.член
1
2 -3
-10
2 1
4
5
0
х2 х св.член
х3+2х2-3х-10=(х-2)(x2+4x +5),
(x-2) (x2+4x +5)=0,
(x-2)=0 или x2+4x +5=0,
Х=2,
2 i ;
x
1
x
Ответ:
2
2 i.
2; 2 i; 2 i.

14. 2. Выбор положительного корня.

2 – действительный положительный корень
уравнения (1)
3. Нахождение параметра а
Подставим число 2 в уравнение
23-a 22+9 2-10=0,
a = 4.
План решения
(2)

15. 4. Решение уравнения (2)

, где а=4 ,
Х=2 – действительный положительный корень.
х3-4х2+9х-10=0
а) Деление многочлена на многочлен
х3-4х2+9х-10 х-2
х3-2х2
х2-2х+5
-2х2 +9х
-2x2+4x
5x-10
5x-10
0
(х-2) (х2-2х+5)=0,
x=2 или
х2-2х+5=0,
D=4-4×5=-16,
x
x
2
1
2 16 2 16 1 2 4i
1 2i;
2
2
2
2 16 2 16 1 2 4i
1 2i.
2
2
2
б) Схема Горнера
2
х3
1
1
х2
х2
х
св.член
-4
9
-10
-2
5
0
х св.член
Ответ: 2 -
План решения
действительный корень уравнения.

16. 5. Решение неравенства

(3)
Решение:
1
x
,
4 x 3 4,
4 x 1,
4
4x 3 4
3
4 x 3 4;
4 x 7;
x 1 .
4
1
4
Ответ :
1
3
4
х
1 3
;
1
;
.
4 4
Отбор корней , удовлетворяющих неравенству (3):
1 3
2 ; 1 ; .
4 4
План решения

17. 6. Упрощение выражения

(4)
Решение:
а) формула двойного радикала
7 4 3
7 49 48
7 49 48
2
2
7 1
7 1
2 3.
2
2
b) выделение квадрата двучлена
7 4 3 22 2 2 3 ( 3) 2 (2 3) 2 2 3 2 3,
2
3 0.
План решения

18. 7. Сравнение значений действительных корней со значением выражения (4)

Сравните 2
и
2 3
.
2
<
2 3
.
Ответ на задание:
2
<
2; 1 2i; 1 2i.
2 3
.
План решения

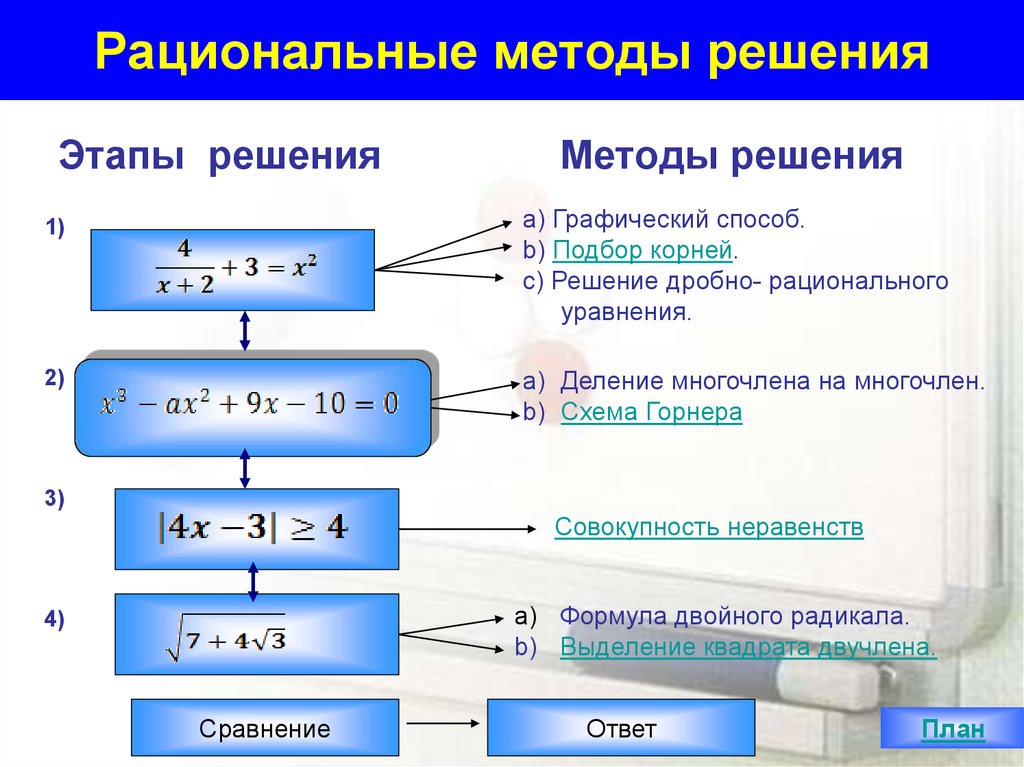
19. Рациональные методы решения

Этапы решения
Методы решения
a) Графический способ.
b) Подбор корней.
c) Решение дробно- рационального
уравнения.
1)
a) Деление многочлена на многочлен.
b) Схема Горнера
2)
3)
Совокупность неравенств
a) Формула двойного радикала.
b) Выделение квадрата двучлена.
4)
Сравнение
Ответ
План

20. Литература

1.
2.
Алгебра: учеб. для 8 кл. общеобразоват. учреждений /[C.М.
Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин] –
5-е изд.- М.: Просвещение, 2007 -287с.
Макарычев Ю.Н. и др.
Алгебра. 8 кл.: Учебник для школ и кл. с углубл. изучением
математики / Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков.3-е изд., испр. –М.: Мнемозина, 2003.-367с.: ил.
3.
Организация проектной деятельности в школе: система
работы/ авт. сост. С.Г. Щербакова и др.- Волгоград: Учитель,
2009 -189 с.
4.
«Обучение для будущего»(при поддержке Microsoft):
Учеб.пособие.-5-е изд., испр. –М.: Издательство-торговый дом
«Русская редакция», 2005 -368 с.