Готовимся к ЕГЭ. Задача С2. Задачи, где присутствует построение сечения

1. Готовимся к ЕГЭ. Задача С2. Задачи, где присутствует построение сечения

2.

Основная волна (июнь – Центр)
Основная волна (июнь – Сибирь)
Вторая волна (резервный день)
Задачи из тренировочных работ 2013-2014 (alexlarin.net)
1
2
3
4
Критерии.
Обоснованно получен правильный ответ (2 балла).
Решение содержит обоснованный переход к планиметрической задаче,
но получен неверный ответ или решение не закончено, или при
правильном ответе решение недостаточно обосновано (1 балл).
Решение не соответствует ни одному из критериев, перечисленных
выше (0 баллов).
Максимальный балл 2

3.

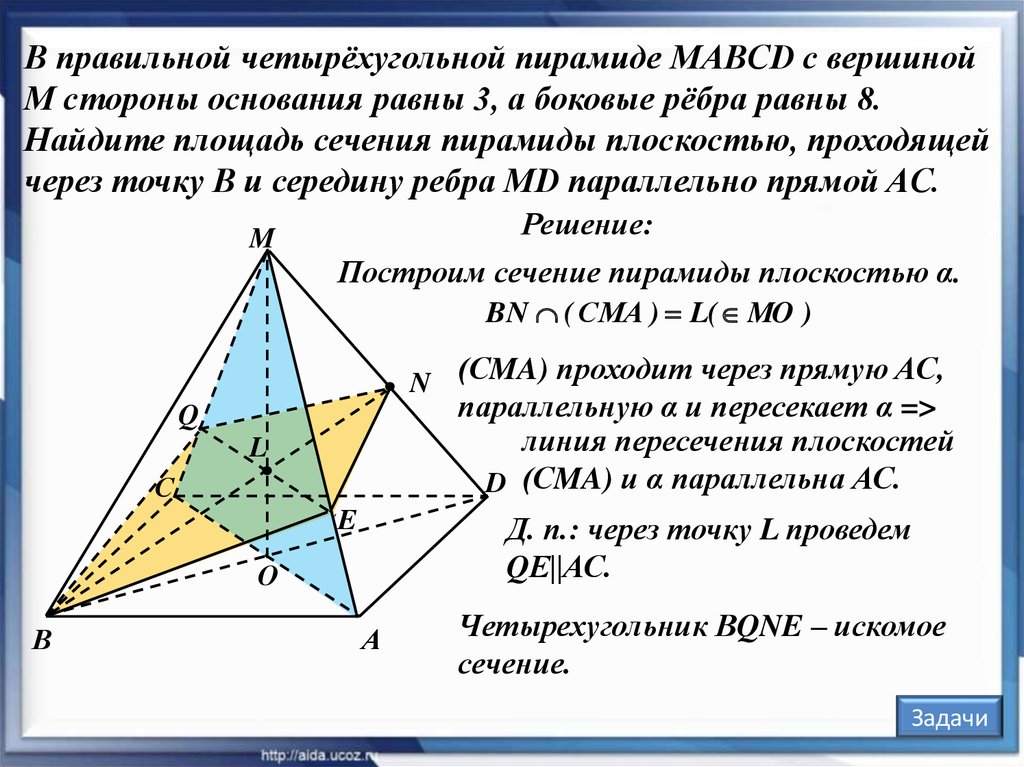
В правильной четырёхугольной пирамиде MABCD с вершиной
M стороны основания равны 3, а боковые рёбра равны 8.
Найдите площадь сечения пирамиды плоскостью, проходящей
через точку B и середину ребра MD параллельно прямой AC.
Решение:
M
Построим сечение пирамиды плоскостью α.
BN ( СMA ) L( MO )
N (СMA) проходит через прямую АС,
параллельную α и пересекает α =>
линия пересечения плоскостей
D (СMA) и α параллельна АС.
Q
L
С
E
Д. п.: через точку L проведем
QЕ||АС.
О
В
А
Четырехугольник ВQNE – искомое
сечение.
Задачи

4.

В правильной четырёхугольной пирамиде MABCD с вершиной
M стороны основания равны 3, а боковые рёбра равны 8.
Найдите площадь сечения пирамиды плоскостью, проходящей
через точку B и середину ребра MD параллельно прямой AC.
Решение:
M
BD AC 3 2 (диагональ квадрата)
N
Q
BN медиана треугольника BMD =>
L
D BN 1 2 BD2 2 MB 2 MD 2
2
1
2 ( 3 2 )2 2 8 2 8 2 5
2
С
E
О
В
А
Задачи

5.

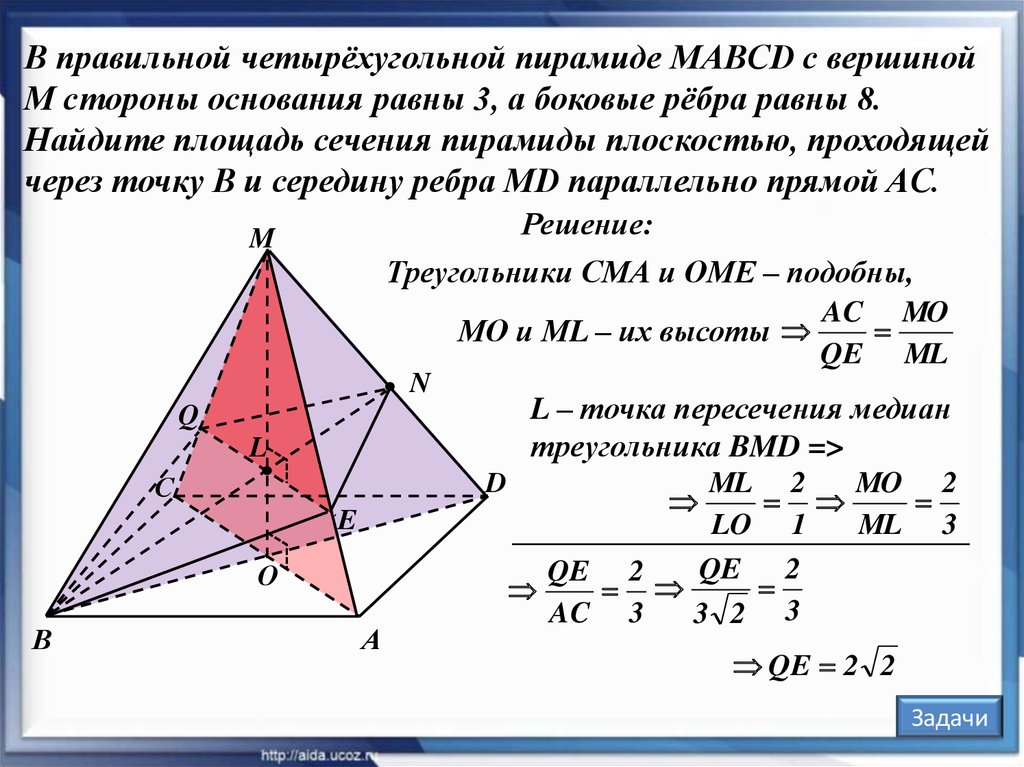
В правильной четырёхугольной пирамиде MABCD с вершиной
M стороны основания равны 3, а боковые рёбра равны 8.
Найдите площадь сечения пирамиды плоскостью, проходящей
через точку B и середину ребра MD параллельно прямой AC.
Решение:
M
Треугольники СМА и ОМЕ – подобны,
AC MO
МО и МL – их высоты
QE ML
N
L – точка пересечения медиан
треугольника BMD =>
Q
L
С
D
E
О
В
А
ML 2
MO 2
LO 1
ML 3
QE 2
QE 2
AC 3
3 2 3
QE 2 2
Задачи

6.

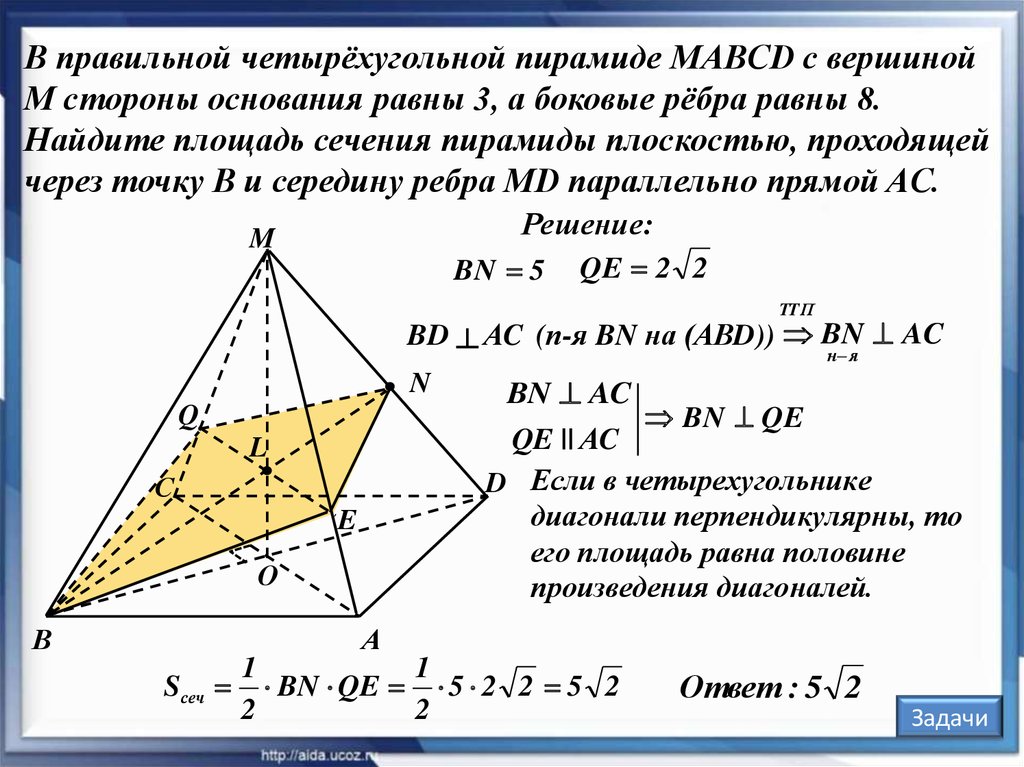
В правильной четырёхугольной пирамиде MABCD с вершиной
M стороны основания равны 3, а боковые рёбра равны 8.
Найдите площадь сечения пирамиды плоскостью, проходящей
через точку B и середину ребра MD параллельно прямой AC.
Решение:
M
BN 5
QE 2 2
TTП
BD ┴ АC (п-я BN на (АВD)) BN AC
н я
N
Q
L
С
E
О
В
BN AC
BN QE
QE || АC
D Если в четырехугольнике
диагонали перпендикулярны, то
его площадь равна половине
произведения диагоналей.
А
Sсеч
1
1
BN QE 5 2 2 5 2
2
2
Ответ : 5 2
Задачи

7.

В правильной четырехугольной призме ABCDA1B1C1D1
сторона основания равна 6, а боковое ребро АА1=1. Точка F
принадлежит ребру C1D1 и делит его в отношении 2:1, считая
от вершины С1. Найдите площадь сечения этой призмы
плоскостью, проходящей через точки А, С и F.
D1
F
2
4
С1 Решение:
Построим сечение.
К
А1
С
D
В1 Секущая плоскость пересекает
параллельные грани параллелепипеда
по параллельным прямым.
Д. п.: FK || AC.
В
Трапеция AKFC – искомое сечение.
А
Задачи

8.

В правильной четырехугольной призме ABCDA1B1C1D1
сторона основания равна 6, а боковое ребро АА1=1. Точка F
принадлежит ребру C1D1 и делит его в отношении 2:1, считая
от вершины С1. Найдите площадь сечения этой призмы
плоскостью, проходящей через точки А, С и F.
F
2
D1
4
С1 Решение: AC 6 2 (диагональ квадрата)
Треугольники KD1F и ADC подобны
К
В1
А1
С
1
D
KF 1
D1 K 1
KF 2 2
D1 K 2
6
3
6 2 3
2
L
В
4
А
Из треугольника KLA:
KA 12 4 2 17
KF D1 K D1F 2 1
AC
DA
DC 6 3
Д. п.: LK || AA1.
Из треугольника FC1C:
FC 4 2 12 17
Задачи

9.

В правильной четырехугольной призме ABCDA1B1C1D1
сторона основания равна 6, а боковое ребро АА1=1. Точка F
принадлежит ребру C1D1 и делит его в отношении 2:1, считая
от вершины С1. Найдите площадь сечения этой призмы
плоскостью, проходящей через точки А, С и F.
F
D1
С1 Решение: AC 6 2
KA 17
К
В1
А1
D
К
С
KH ( 17 )2 ( 2 2 )2 3
FC 17
2 2
17
В
А
Из треугольника KHA:
KF 2 2
17
А 2 2
H
Sсеч
F
С
6 2
( 2 2 6 2 ) 3
12 2
2
Ответ : 12 2
Задачи

10.

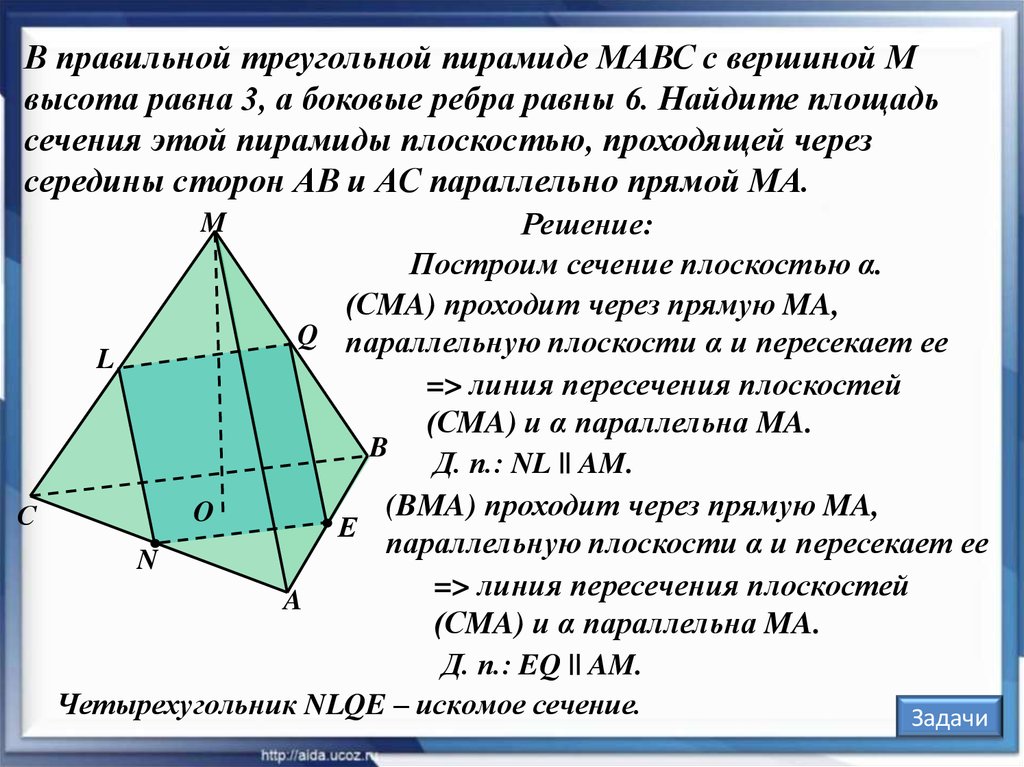
В правильной треугольной пирамиде МАВС с вершиной М
высота равна 3, а боковые ребра равны 6. Найдите площадь
сечения этой пирамиды плоскостью, проходящей через
середины сторон АВ и АС параллельно прямой МА.
Решение:
Построим сечение плоскостью α.
(СMA) проходит через прямую MA,
Q параллельную плоскости α и пересекает ее
L
=> линия пересечения плоскостей
(СMA) и α параллельна MA.
B
Д. п.: NL || AM.
(BMA) проходит через прямую MA,
O
С
Е
параллельную плоскости α и пересекает ее
N
=> линия пересечения плоскостей
A
(СMA) и α параллельна MA.
Д. п.: EQ || AM.
Четырехугольник NLQE – искомое сечение.
Задачи
M

11.

В правильной треугольной пирамиде МАВС с вершиной М
высота равна 3, а боковые ребра равны 6. Найдите площадь
сечения этой пирамиды плоскостью, проходящей через
середины сторон АВ и АС параллельно прямой МА.
Т. Фалеса
Решение:
M
NL || AM, NL – средняя
CN=NA линия
Q
треугольника
СМА
EQ || AM,
EQ – средняя
L
С
O
N
1
MA
2
EQ
1
MA
2
линия
треугольника BМА
B
NL= и ||
NLQE –
TTП
EQ
параллелограмм
E
АH ┴ CВ (п-я MA на (АВC)) MA CB
н я
MA CB
A
MA || NL NL NE => NLQE – прямоугольник
CB || NE
AE=EB
H
NL
Задачи

12.

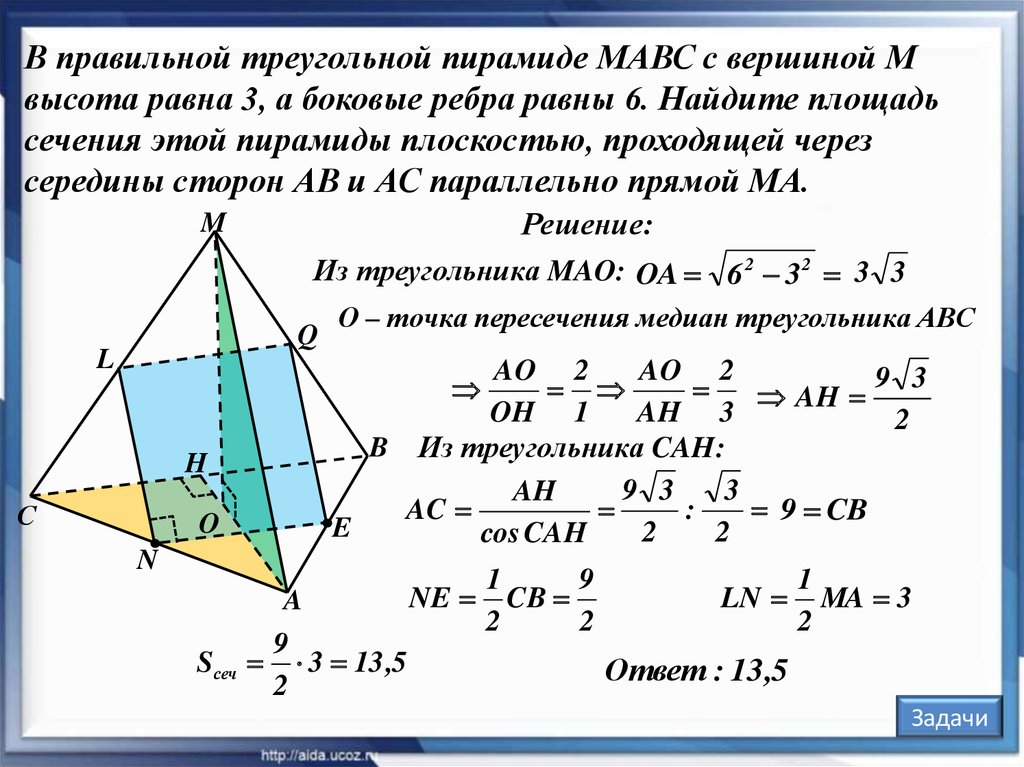
В правильной треугольной пирамиде МАВС с вершиной М
высота равна 3, а боковые ребра равны 6. Найдите площадь
сечения этой пирамиды плоскостью, проходящей через
середины сторон АВ и АС параллельно прямой МА.
Решение:
Из треугольника MAO: OA 6 2 32 3 3
M
Q
L
AO 2
AO 2
9 3
AH
OH 1
AH 3
2
B Из треугольника CAH:
9 3
3
AH
:
9 CB
AC
E
2
2
cos CAH
H
С
О – точка пересечения медиан треугольника АВС
O
N
A
Sсеч
9
3 13 ,5
2
NE
1
9
CB
2
2
LN
1
MA 3
2
Ответ : 13 ,5
Задачи

13.

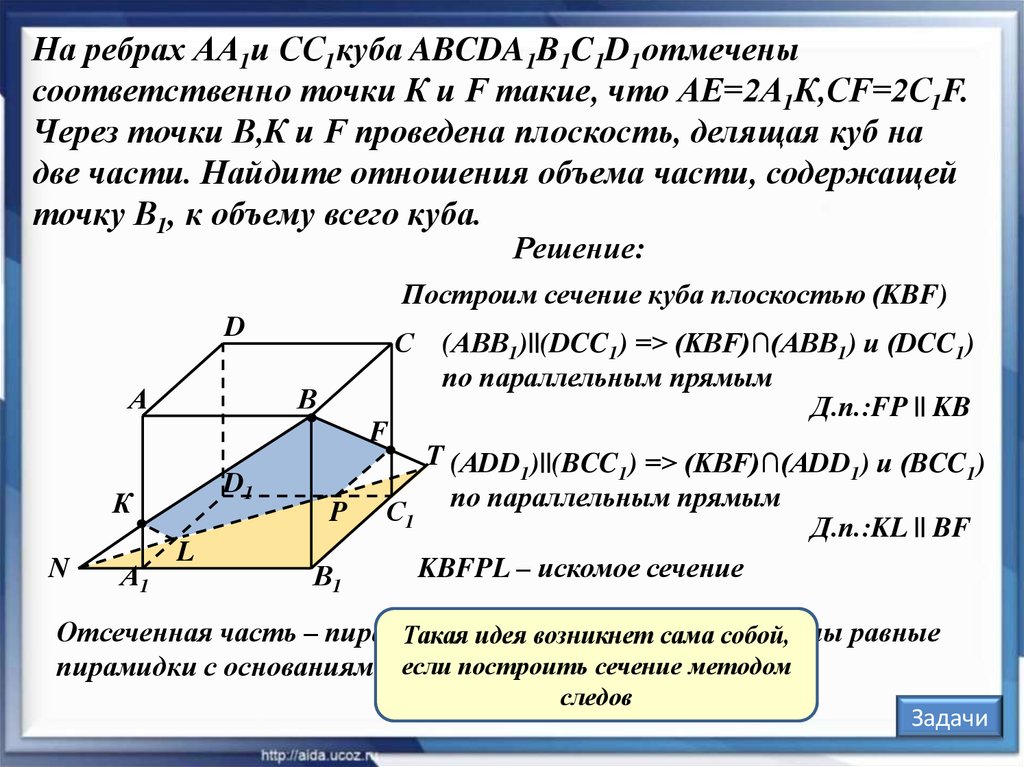
На ребрах АА1и СС1куба ABCDA1B1C1D1отмечены
соответственно точки К и F такие, что АЕ=2А1К,CF=2C1F.
Через точки В,К и F проведена плоскость, делящая куб на
две части. Найдите отношения объема части, содержащей
точку В1, к объему всего куба.
Решение:
Построим сечение куба плоскостью (KBF)
D
А
С
В
F
D1
К
N
А1
L
P
В1
(АВВ1)||(DCC1) => (KBF)∩(АВВ1) и (DCC1)
по параллельным прямым
Д.п.:FP || KB
T (АDD )||(BCC ) => (KBF)∩(АDD ) и (BCC )
1
1
1
1
С1 по параллельным прямым
Д.п.:KL || BF
KBFPL – искомое сечение
Отсеченная часть – пирамида
от которой
равные
ТакаяBNB
идея1D,
возникнет
сама отрезаны
собой,
если 1построить
пирамидки с основаниями NLA
и PTC1 сечение методом
следов
Задачи

14.

На ребрах АА1и СС1куба ABCDA1B1C1D1отмечены
соответственно точки К и F такие, что АЕ=2А1К,CF=2C1F.
Через точки В,К и F проведена плоскость, делящая куб на
две части. Найдите отношения объема части, содержащей
точку В1, к объему всего куба.
Решение:
Пусть ребро куба = 3, тогда Vкуба 27 Треугольник NBB1 подобен
треугольнику NKA1 k=3/1
D
С
1
1
NA1 NB1
NA1 ( NA1 3 )
3
3
А
В
3
3
9
F
NA
NB
3
1
1
T
2
2
2
D1
9
К
P С1
Аналогично: B1T
2
L
N
1
1 1 9 9
81
А1
В1 V
S
BB
3
BNTB1
NTB1
1
3
3 2 2 2
8
Найдем объемы маленьких равных пирамид
Задачи

15.

На ребрах АА1и СС1куба ABCDA1B1C1D1отмечены
соответственно точки К и F такие, что АЕ=2А1К,CF=2C1F.
Через точки В,К и F проведена плоскость, делящая куб на
две части. Найдите отношения объема части, содержащей
точку В1, к объему всего куба.
Решение:
81
8
С Найдем объемы маленьких равных пирамид
Vкуба 27
D
А
В
F
D1
К
N
А1
L
P
В1
С1
VBNTB1
Они подобны пирамиде BNB1T k=3/1
T
=> их объемы относятся как k3=27/1
VKA1 LN
1
3
SBNB1T
27
8
Задачи

16.

На ребрах АА1и СС1куба ABCDA1B1C1D1отмечены
соответственно точки К и F такие, что АЕ=2А1К,CF=2C1F.
Через точки В,К и F проведена плоскость, делящая куб на
две части. Найдите отношения объема части, содержащей
точку В1, к объему всего куба.
Решение:
Vкуба 27
D
А
С
Vмал
В
F
D1
К
N
А1
L
P
В1
T
пир
VBNTB1
81
8
3
8
Vмногогранника VBNTB1 VNA1 LK VTC 1FP
С1
81 3 3 75
8 8 8
8
75
75 1
25
: 27
8
8 27 72
Vмногогранника
Vкуба
Ответ :
25
72
Задачи

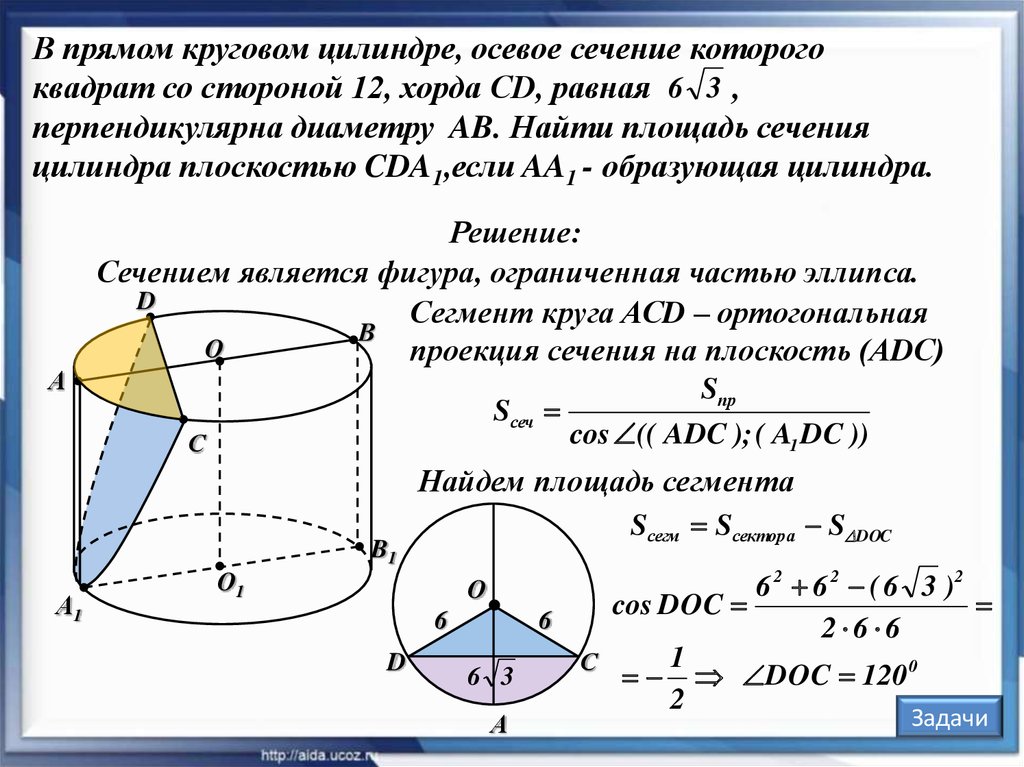
17.

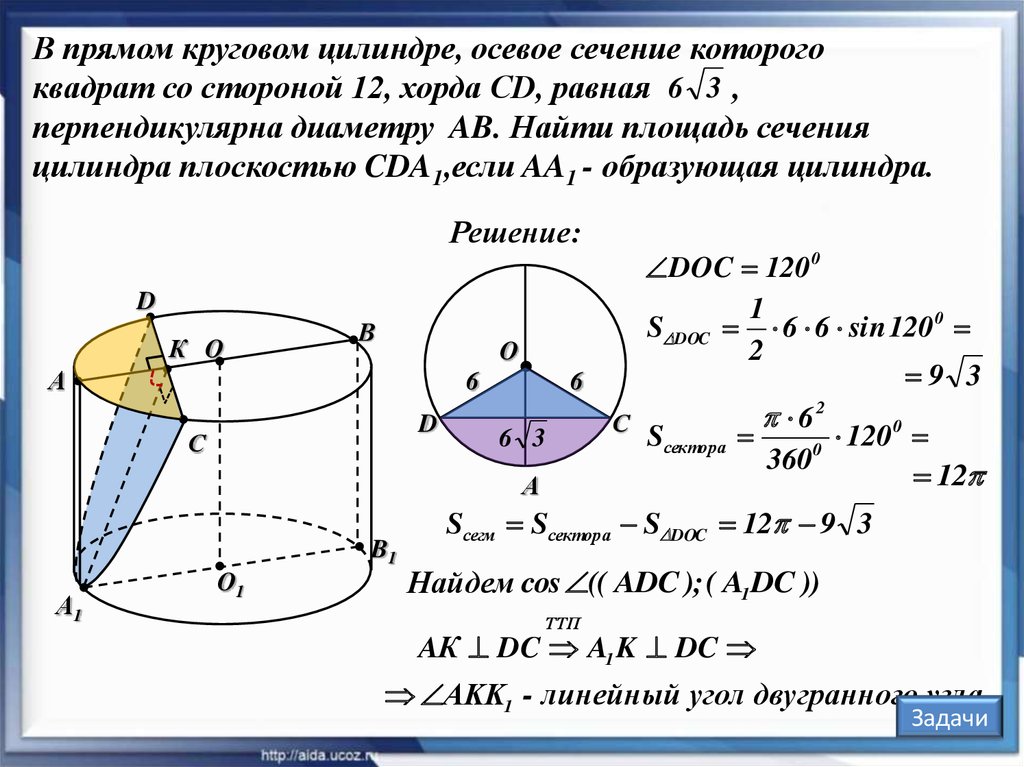
В прямом круговом цилиндре, осевое сечение которого
квадрат со стороной 12, хорда CD, равная 6 3 ,
перпендикулярна диаметру AB. Найти площадь сечения
цилиндра плоскостью CDA1,если AA1 - образующая цилиндра.
Решение:
Сечением является фигура, ограниченная частью эллипса.
D
Сегмент круга АСD – ортогональная
В
O
проекция сечения на плоскость (АDС)
А
Sпр
Sсеч
cos (( ADC ); ( A1 DC ))
С
Найдем площадь сегмента
Sсегм Sсектора S DOC
B1
А1
O1
6 2 6 2 ( 6 3 )2
cos DOC
6
6
2 6 6
1
D
С
6 3
DOC 120 0
2
O
А
Задачи

18.

В прямом круговом цилиндре, осевое сечение которого
квадрат со стороной 12, хорда CD, равная 6 3 ,
перпендикулярна диаметру AB. Найти площадь сечения
цилиндра плоскостью CDA1,если AA1 - образующая цилиндра.
Решение:
DOC 120 0
1
S DOC 6 6 sin 120 0
O
2
9 3
6
6
62
D
С
0
Sсектора
120
6 3
0
360
12
А
D
К O
В
А
С
B1
А1
O1
Sсегм Sсектора S DOC 12 9 3
Найдем cos (( ADC ); ( A1 DC ))
ТТП
AК DC A1 K DC
АKK1 - линейный угол двугранного угла
Задачи

19.

В прямом круговом цилиндре, осевое сечение которого
квадрат со стороной 12, хорда CD, равная 6 3 ,
перпендикулярна диаметру AB. Найти площадь сечения
цилиндра плоскостью CDA1,если AA1 - образующая цилиндра.
Sсегм 12 9 3
Решение:
Косинус искомого угла найдем из
треугольника А1АК
D
В
К O
А
O
6
300
D
С
А
K
3
А1
A1 K 12 2 3 2 3 17
3
1
cos АKK1
3 17
17
А1
Sсеч
Sпр
cos AKK1
С
K
12
B1
O1
6
1
OK 6 3
2
AK 6 3 3
17 ( 12 9 3 ) 3 17 ( 4 3 3 )
Задачи

20.

В прямом круговом цилиндре, осевое сечение которого
квадрат со стороной 12, хорда CD, равная 6 3 ,
перпендикулярна диаметру AB. Найти площадь сечения
цилиндра плоскостью CDA1,если AA1 - образующая цилиндра.
Решение:
D
O
А
В
К
С
Решение второго случая (хорда
пересекает диаметр между
точками О и В) аналогично.
B1
А1
O1
Ответ : 3 17 ( 4 3 3 );5( 8 3 3 )
Задачи

21.

Радиус основания конуса равен 5, а его высота равна 12.
Плоскость сечения содержит вершину конуса и хорду
основания, длина которой равна 6. Найдите расстояние от
центра основания конуса до плоскости сечения.
S
Решение:
ТТП
Д.п.: OH AB SH AB
( OHS ) ( ASB ) ( O ; ( ASB )) OM SH
OM найдем из треугольника SOH
SO=12, найдем ОН
M
А
H
O
O
5
5
В
А
Треугольник ОНВ – египетский
H
3
OH 4
В
Задачи

22.

Радиус основания конуса равен 5, а его высота равна 12.
Плоскость сечения содержит вершину конуса и хорду
основания, длина которой равна 6. Найдите расстояние от
центра основания конуса до плоскости сечения.
S
Решение:
OM найдем из треугольника SOH
OH 4
SO=12
S
M
А
O
M
H
В
H
4
SH 12 2 4 2 4 10
1
SSHO 12 4 24
2
1
S
OM SH 24
12 SHO
2
1
OM 4 10 24
2
12
OM
Ответ :
O
10
Задачи

23.

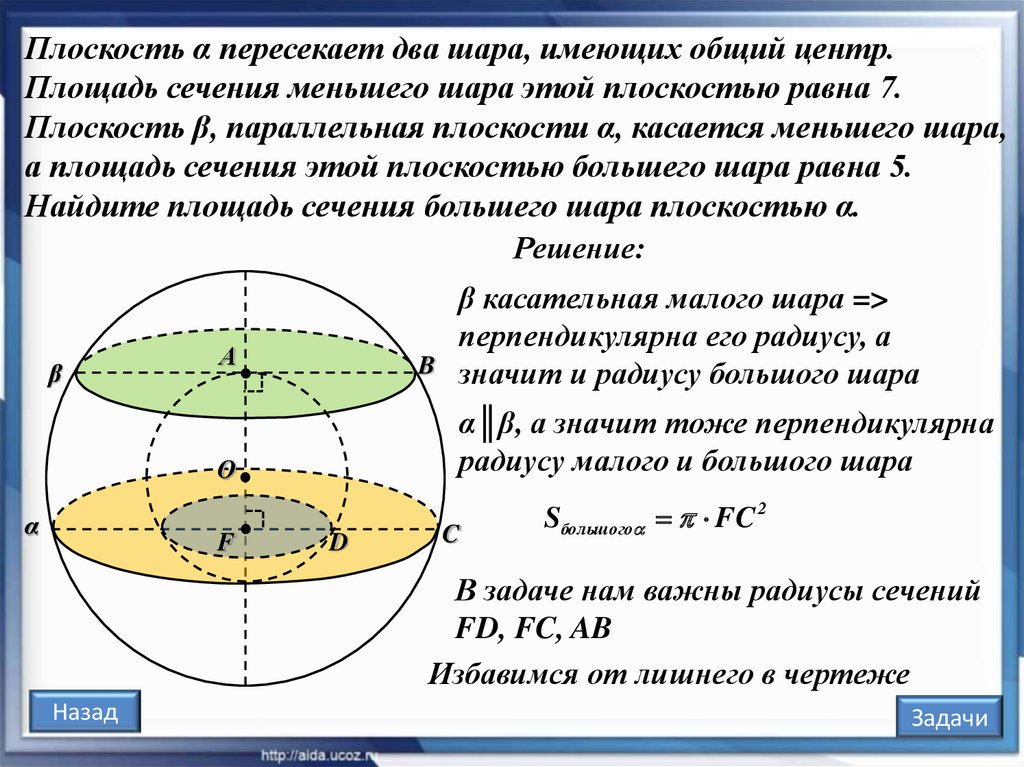
Плоскость α пересекает два шара, имеющих общий центр.
Площадь сечения меньшего шара этой плоскостью равна 7.
Плоскость β, параллельная плоскости α, касается меньшего шара,
а площадь сечения этой плоскостью большего шара равна 5.
Найдите площадь сечения большего шара плоскостью α.
Решение:
β
β касательная малого шара =>
перпендикулярна его радиусу, а
B значит и радиусу большого шара
А
α║β, а значит тоже перпендикулярна
радиусу малого и большого шара
O
α
F
D
C
Sбольшого FC 2
В задаче нам важны радиусы сечений
FD, FC, AB
Избавимся от лишнего в чертеже
Назад
Задачи
24

24.

Плоскость α пересекает два шара, имеющих общий центр.
Площадь сечения меньшего шара этой плоскостью равна 7.
Плоскость β, параллельная плоскости α, касается меньшего шара,
а площадь сечения этой плоскостью большего шара равна 5.
Найдите площадь сечения большего шара плоскостью α.
Решение:
Sбольшого FC 2
β
Sмалого
А
B
O
α
F
D
2
FD 7 FD
2
7
5
Sбольшого AB2 5 АВ2
AO OD - радиусы малого шара
C OB OC
- радиусы большого шара
AOB : AO 2 OB2 AB2
FOD : OD2 OF 2 FD2
Стереометрический чертеж
OB2 AB2 OF 2 FD2
Задачи
25

25.

Плоскость α пересекает два шара, имеющих общий центр.
Площадь сечения меньшего шара этой плоскостью равна 7.
Плоскость β, параллельная плоскости α, касается меньшего шара,
а площадь сечения этой плоскостью большего шара равна 5.
Найдите площадь сечения большего шара плоскостью α.
Решение:
Sбольшого FC 2
FD 2
β
А
B
АВ2
5
D
Стереометрический чертеж
AO OD
OF 2
C OC OF
2
F
5
OB OC
OB2 AB2 OF 2 FD2
OC 2
O
α
7
2
7
5
7
12
OFC : OC 2 OF 2 FC 2
12
Sбольшого FC 2
12
Ответ : 12
Задачи
26

26.

Источники:
КИМ 2013
Тренировочные работы http://alexlarin.net/ege/2013/c2_2013.html
27