Задачи на построение сечений

1. Задачи на построение сечений

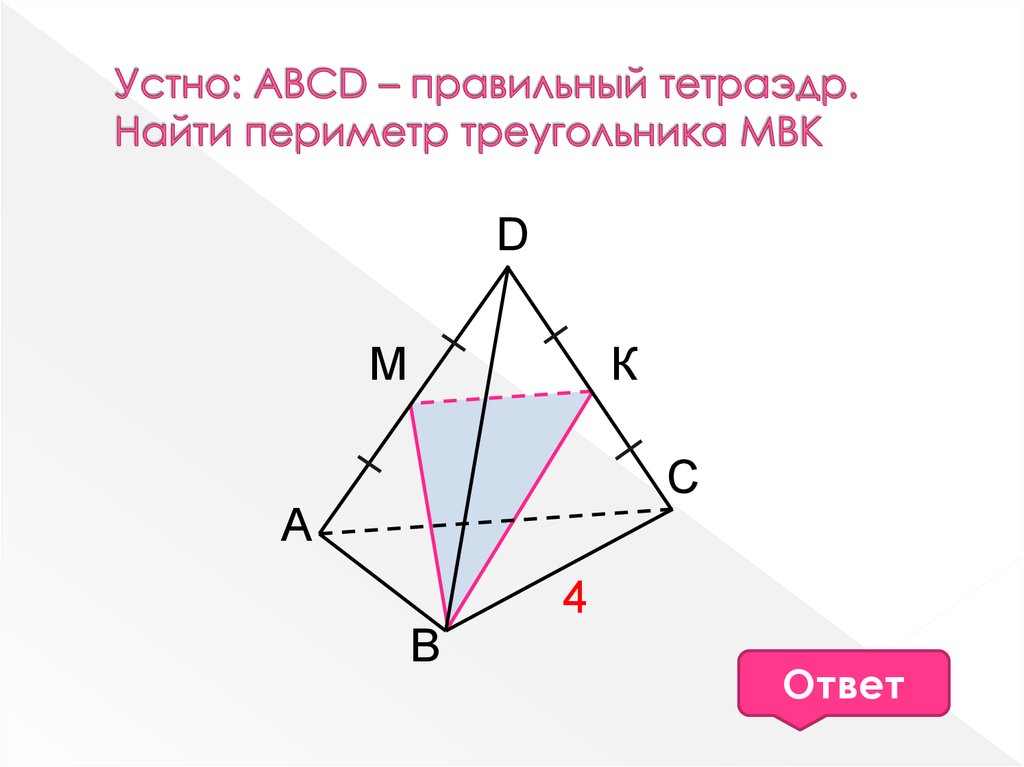
2. Устно: ABCD – правильный тетраэдр. Найти периметр треугольника МВК

D
К
M
C
A
4
B
2Ответ
+4 3

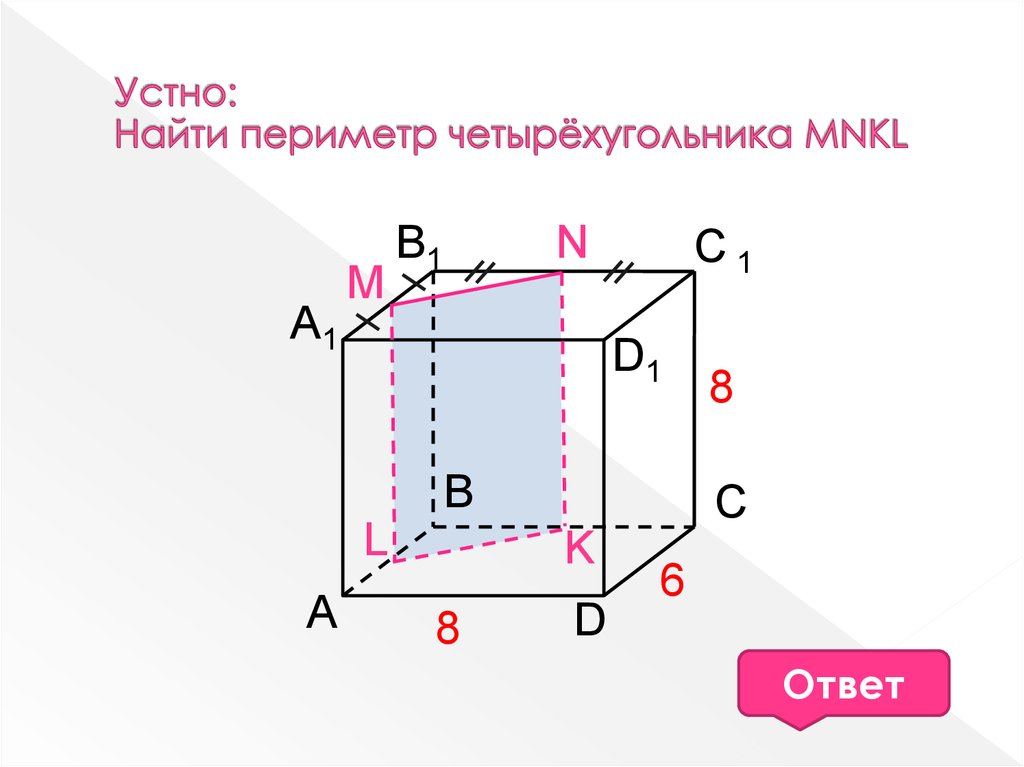
3.

A1
M
В1
С1
N
D1
В
L
A
C
K
8
8
D
6
26
Ответ

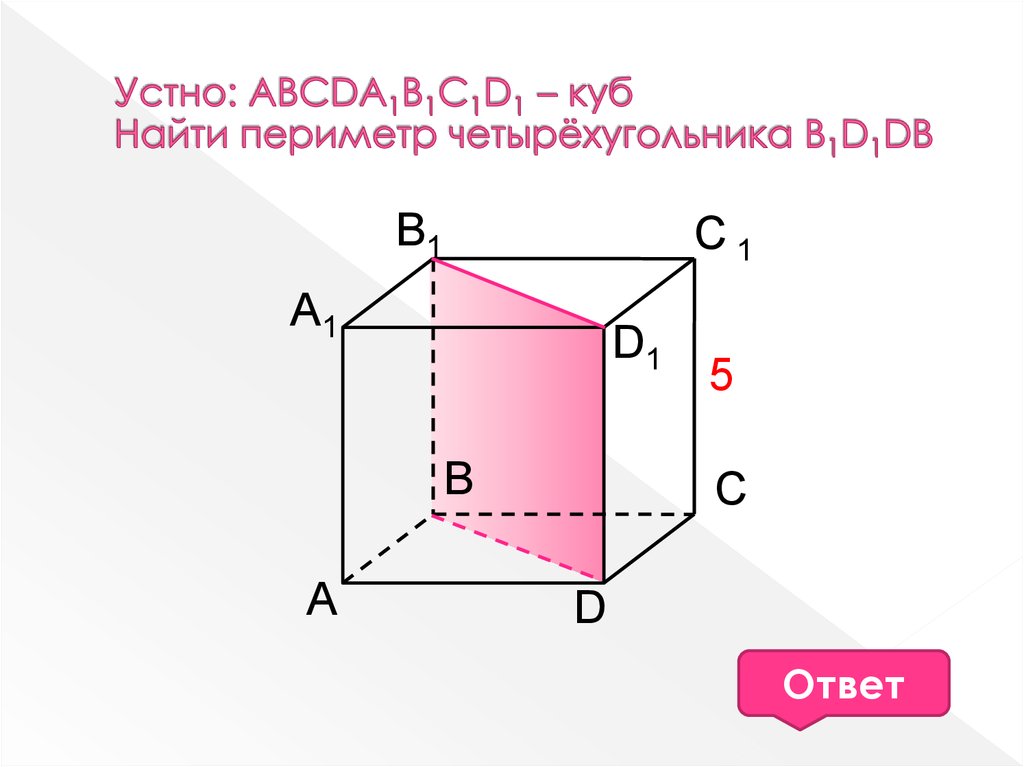
4.

В1
С1
A1
D1
В
A
5
C
D
10Ответ
+ 10 2

5. Определение

Секущей плоскостью тетраэдра (или
параллелепипеда) называется любая
плоскость, по обе стороны от которой
имеются точки данного тетраэдра
(параллелепипеда).
Многоугольник, который будет образован
этими отрезками, называется сечением
тетраэдра (параллелепипеда).

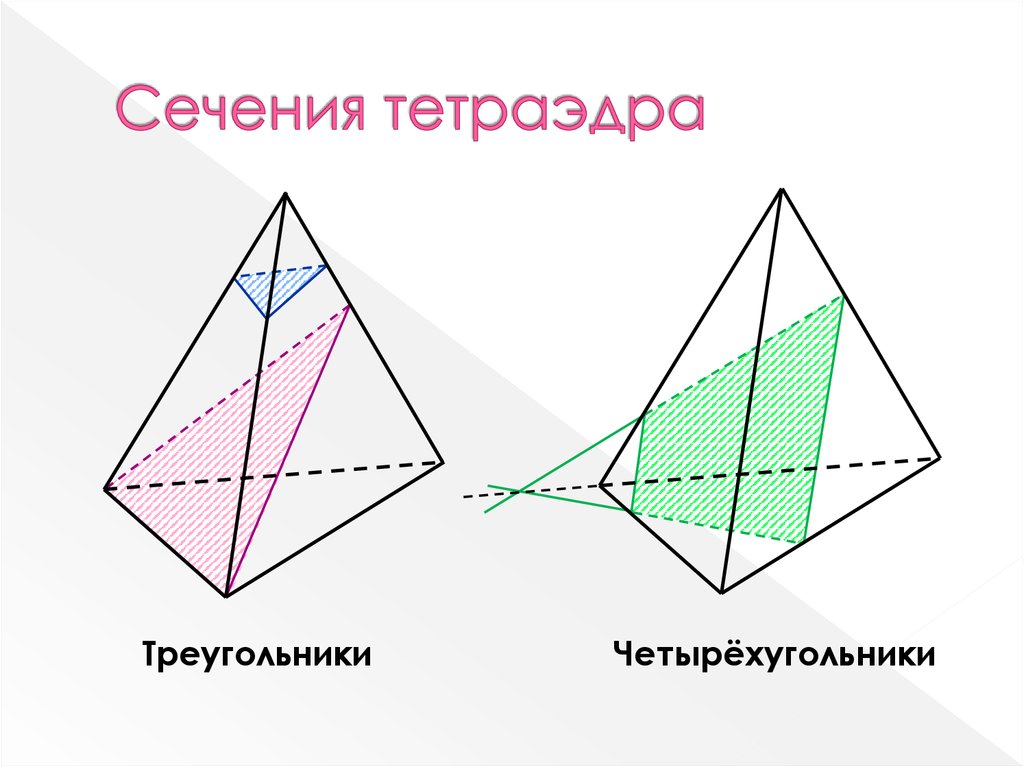
6. Сечения тетраэдра

Треугольники
Четырёхугольники

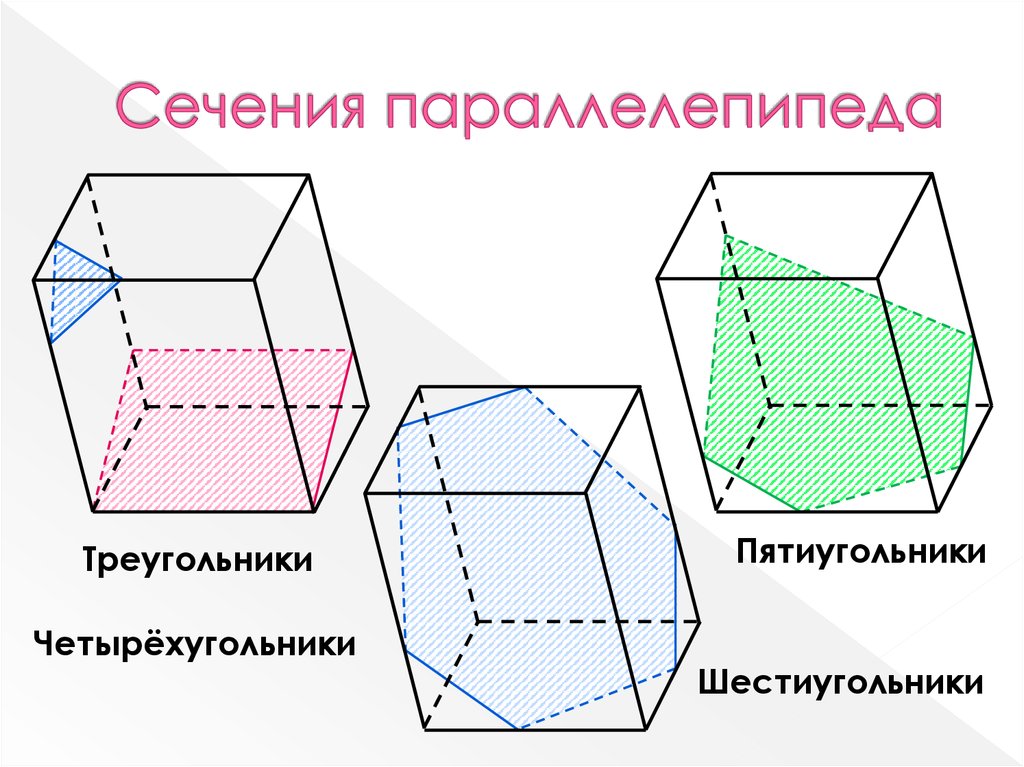
7. Сечения параллелепипеда

Треугольники
Четырёхугольники
Пятиугольники
Шестиугольники

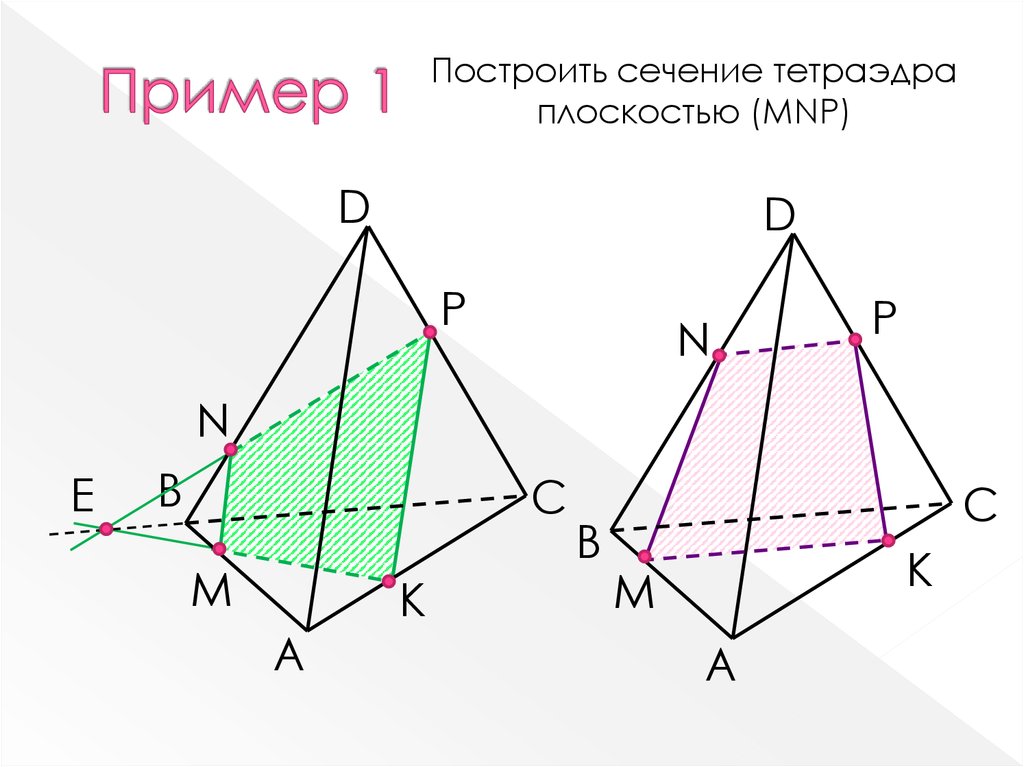
8. Пример 1

Построить сечение тетраэдра
плоскостью (MNP)
D
D
Р
N
Р
N
Е
B
C
M
A
К
B
C
К
M
A

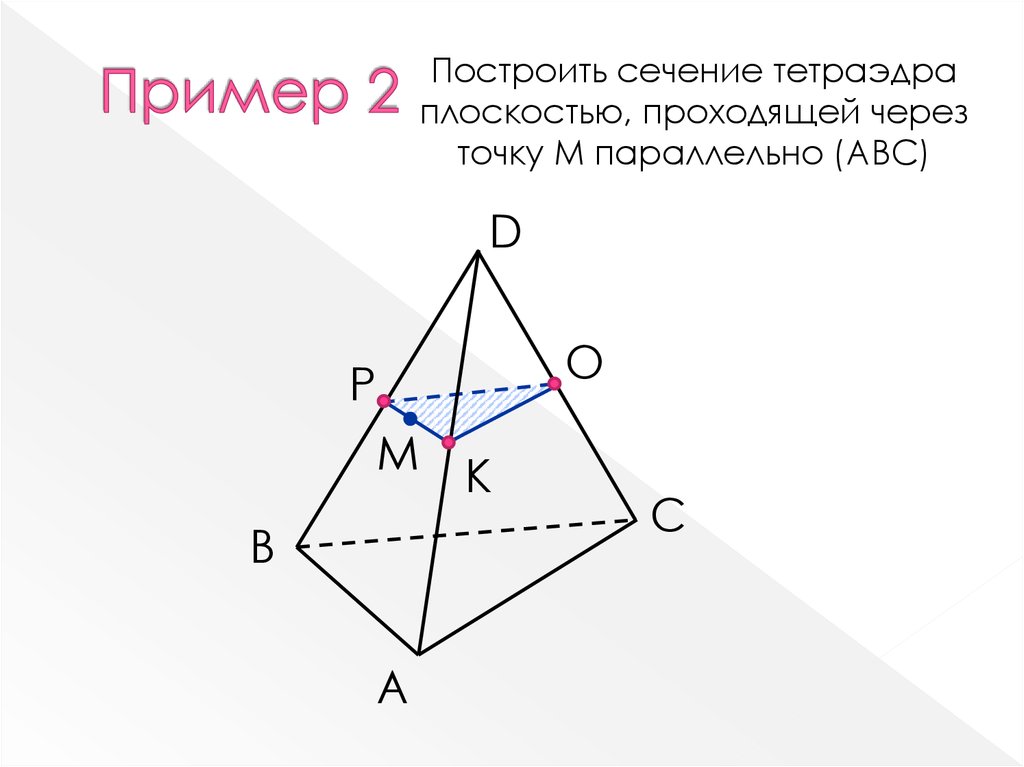
9.

Построить сечение тетраэдра
плоскостью, проходящей через
точку M параллельно (АВС)
D
О
Р
M
B
A
К
С

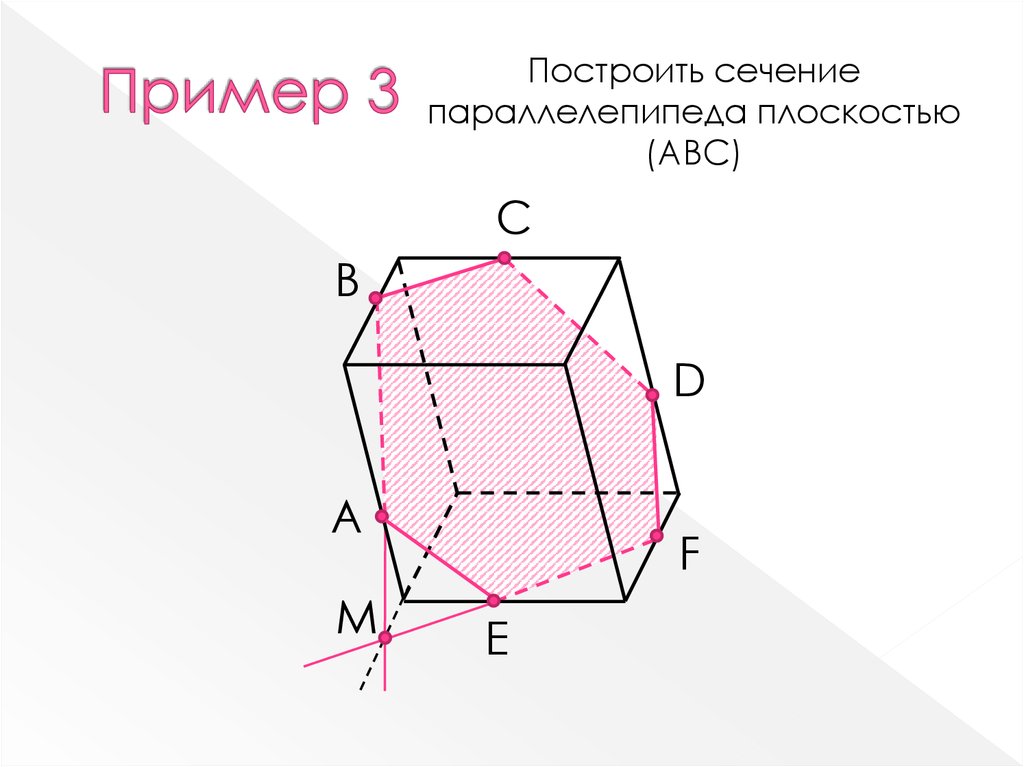
10.

Построить сечение
параллелепипеда плоскостью
(АВС)
B
B
С
С
A
A
E
D

11.

Построить сечение
параллелепипеда плоскостью
(АВС)
С
B
D
A
М
F
E

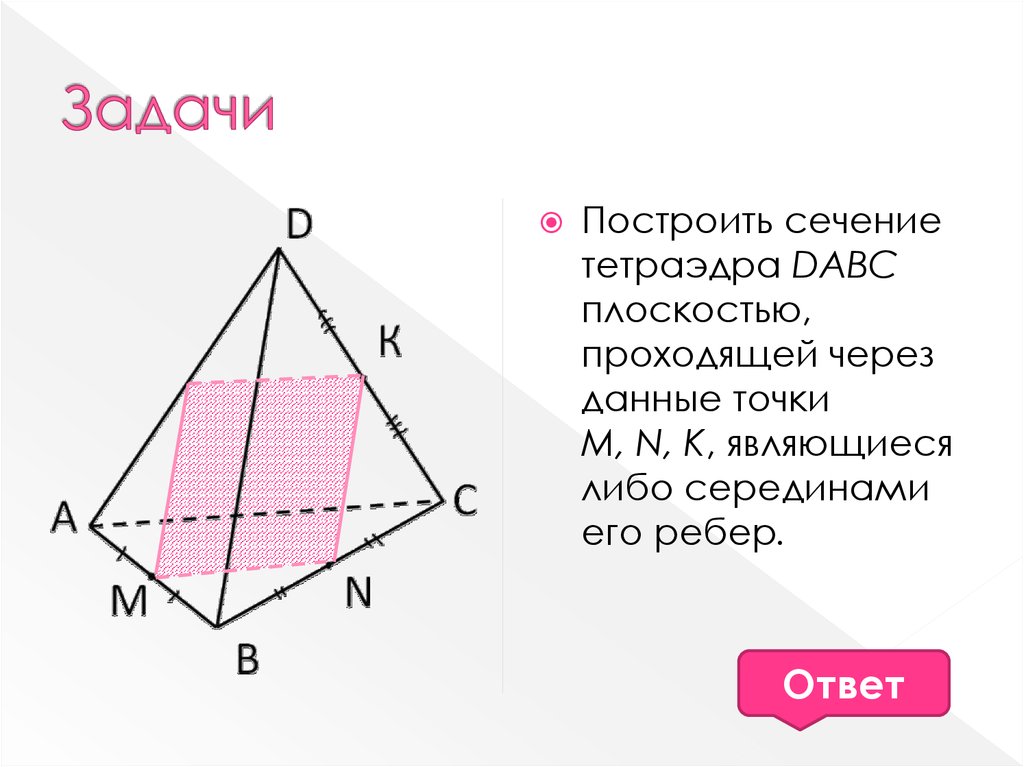
12. Задачи

Построить сечение
тетраэдра DABC
плоскостью,
проходящей через
данные точки
М, N, К, являющиеся
либо серединами
его ребер.
Ответ

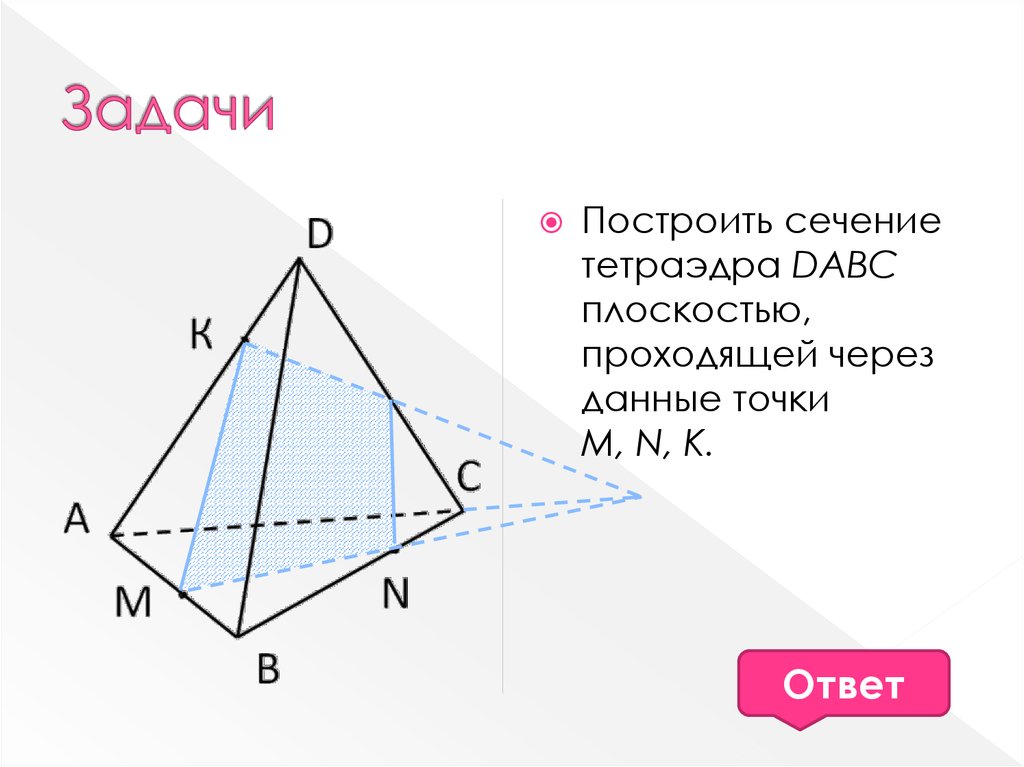
13. Задачи

Построить сечение
тетраэдра DABC
плоскостью,
проходящей через
данные точки
М, N, К.
Ответ

14. Задачи

В1
A1
С1
D1
C
A
Построить сечение
куба плоскостью,
проходящей через
три данные точки
А, С, С1. Найти
периметр сечения,
если ребро куба
равно а
D
Ответ

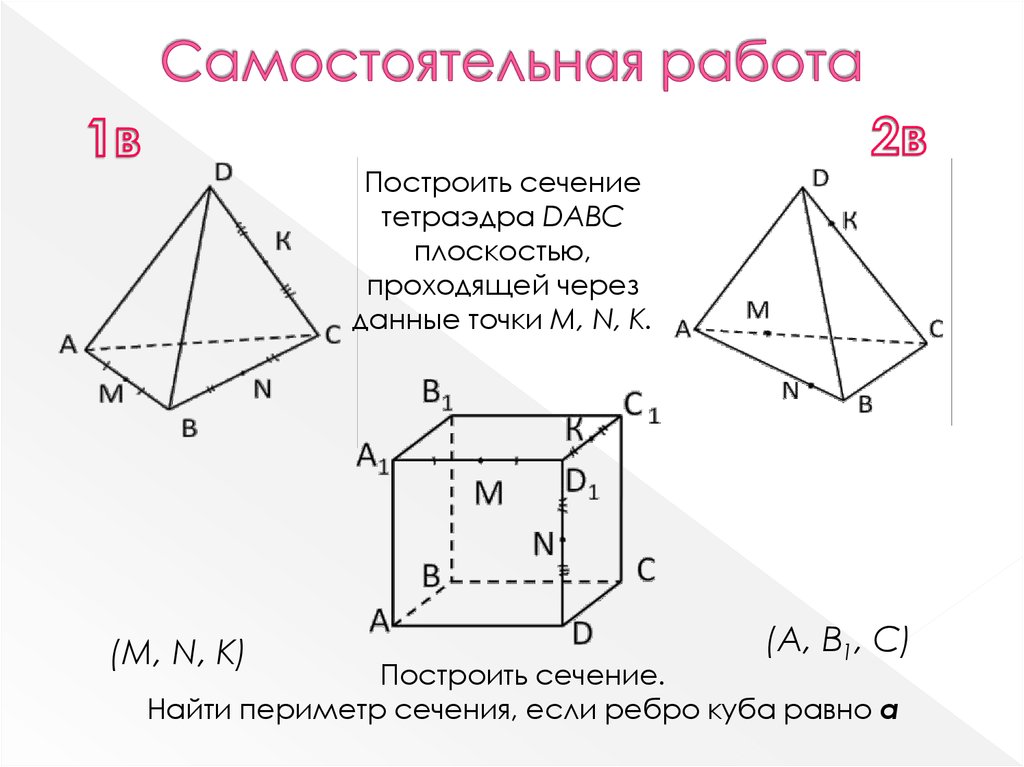
15. Самостоятельная работа

Построить сечение
тетраэдра DABC
плоскостью,
проходящей через
данные точки М, N, К.
(М, N, К)
(А, В1, С)
Построить сечение.
Найти периметр сечения, если ребро куба равно а

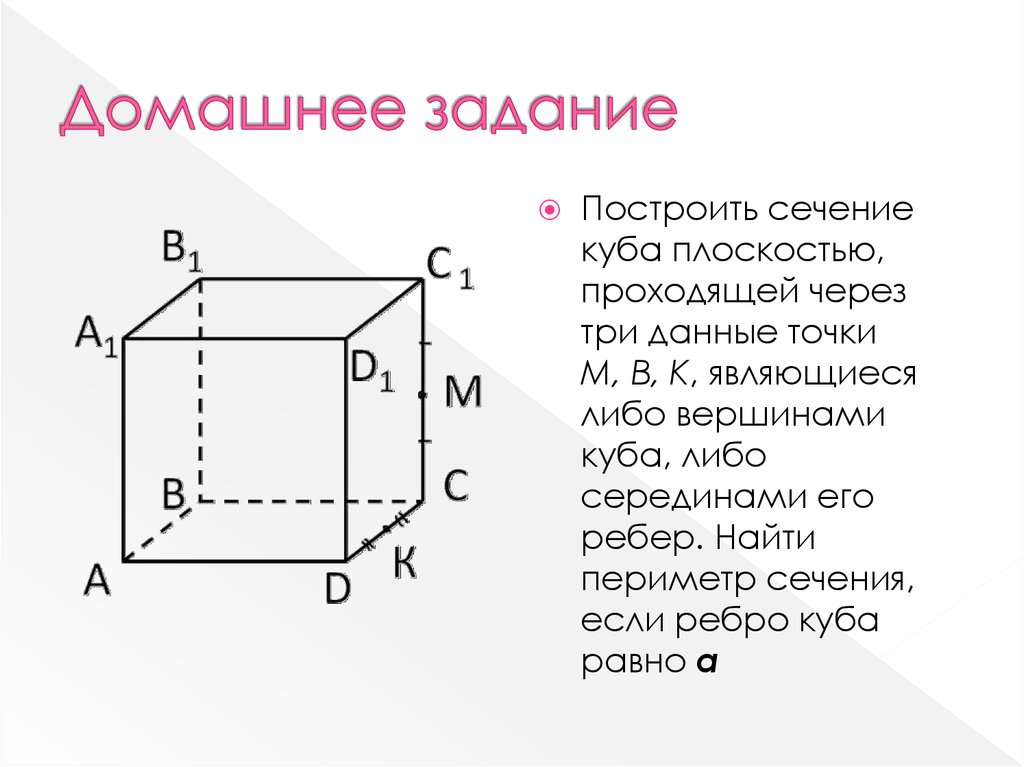
16. Домашнее задание

Построить сечение
куба плоскостью,
проходящей через
три данные точки
М, В, К, являющиеся
либо вершинами
куба, либо
серединами его
ребер. Найти
периметр сечения,
если ребро куба
равно а

17. Литература

Геометрия. 10-11 классы : учеб. для
общеобразоват. учреждений : базовый и
профил. уровни / [Л. С. Атанасян, В. Ф. Бутузов,
С. Б. Кадомцев и др.] М. : Просвещение, 2009.
Поурочные разработки по геометрии: 10 класс/
Сост. В.А. Яровенко. М.: ВАКО, 2010.