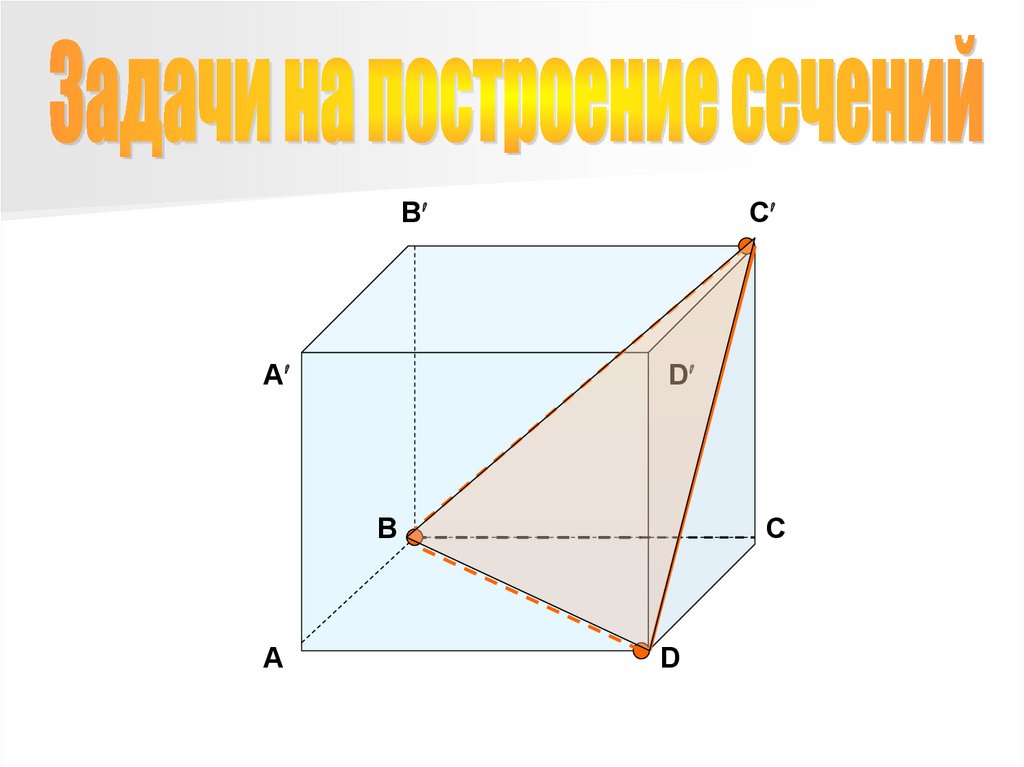
Задачи на построение сечений

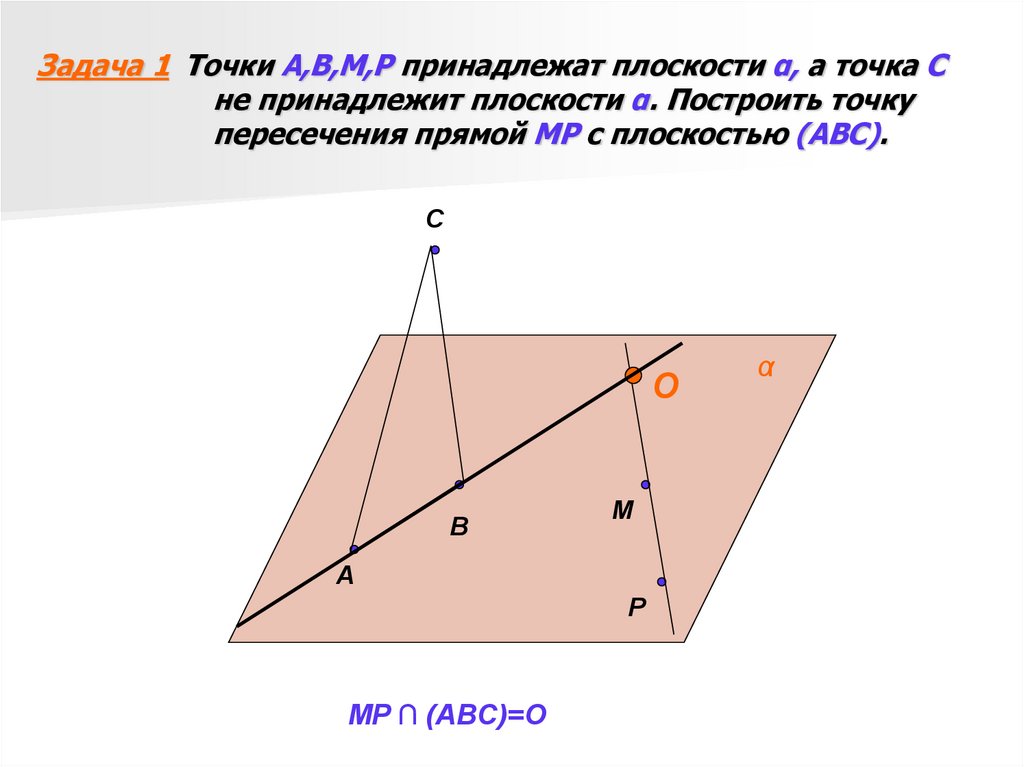
1. Задача 1 Точки А,В,М,Р принадлежат плоскости α, а точка С не принадлежит плоскости α. Построить точку пересечения прямой МР с

плоскостью (АВС).
C
O
B
M
A
P
MP ∩ (ABC)=O
α

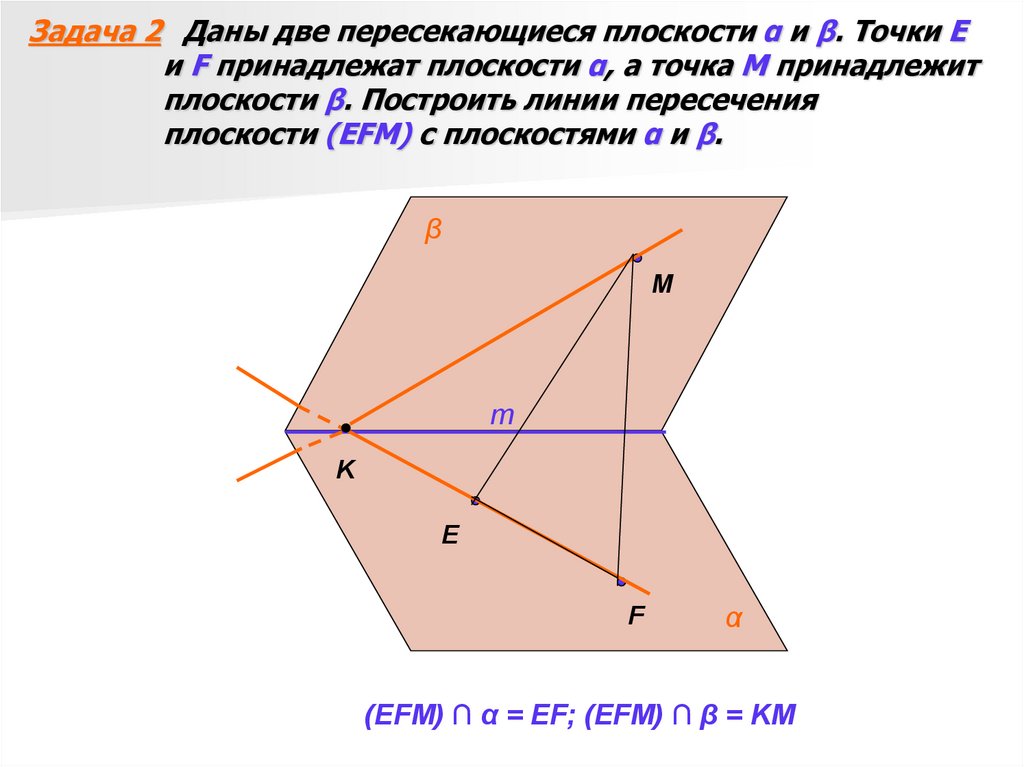
2. Задача 2 Даны две пересекающиеся плоскости α и β. Точки E и F принадлежат плоскости α, а точка М принадлежит плоскости β.

Построить линии пересечения
плоскости (EFM) с плоскостями α и β.
β
M
m
K
E
F
α
(EFM) ∩ α = EF; (EFM) ∩ β = KM

3.

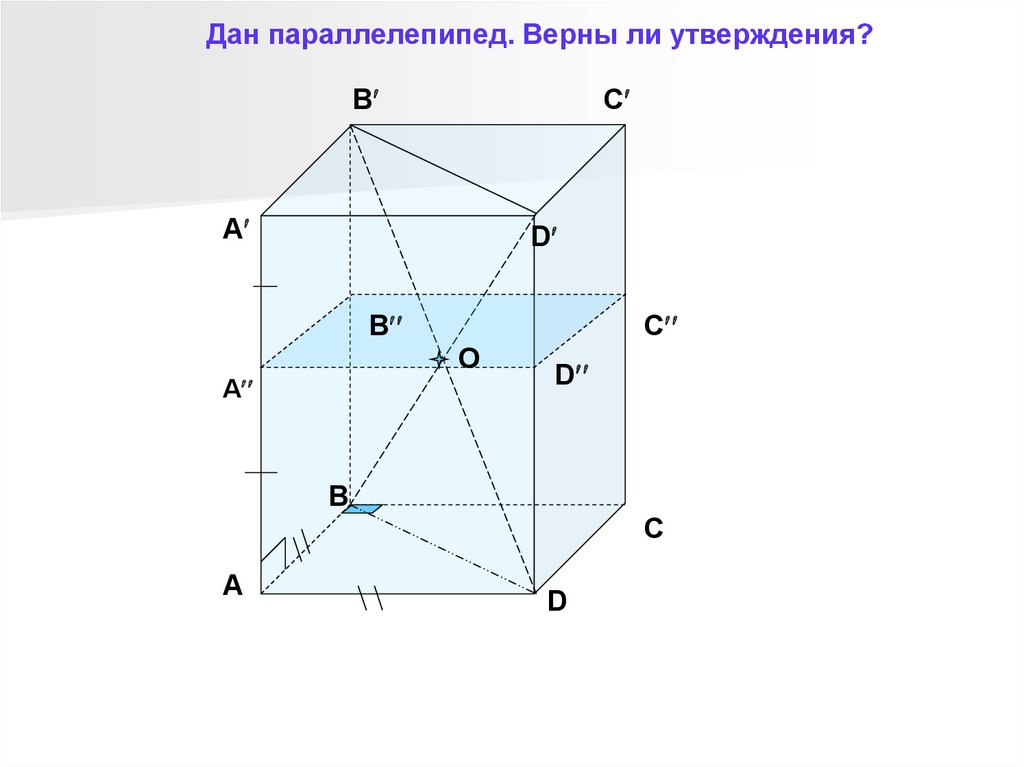
Дан параллелепипед. Верны ли утверждения?
B
C
A
D
B
C
O
A
D
B
C
A
D

4.

B
A
C
D
B
A
C
D

5.

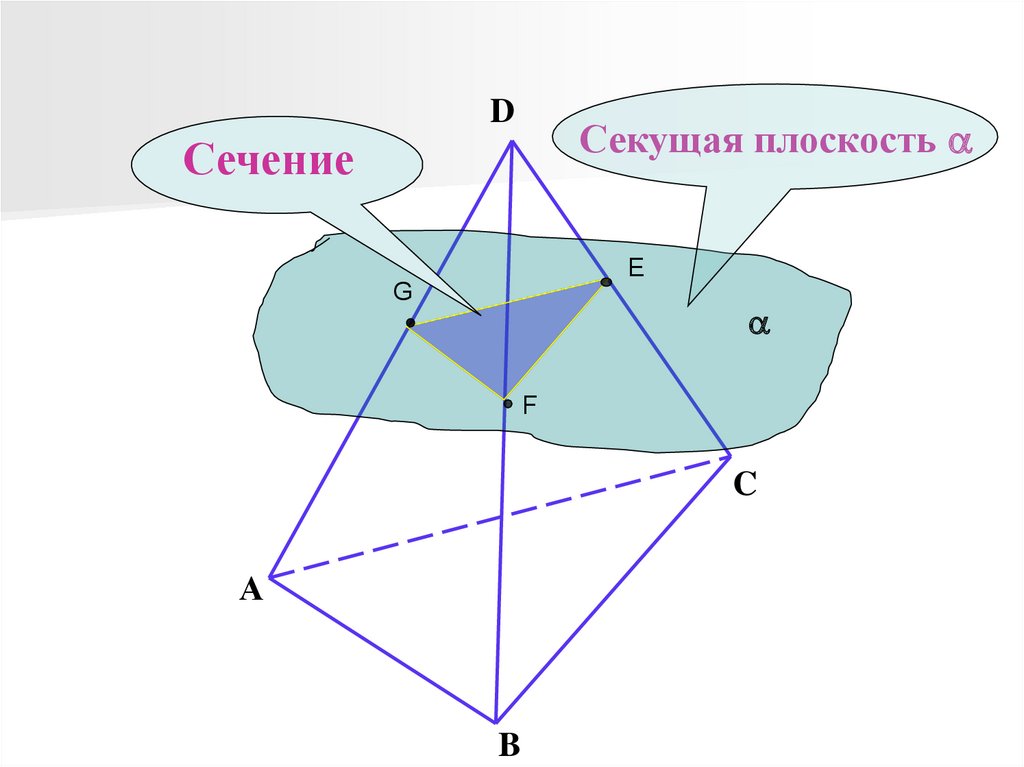
D
Секущая плоскость
Сечение
E
G
F
C
А
B

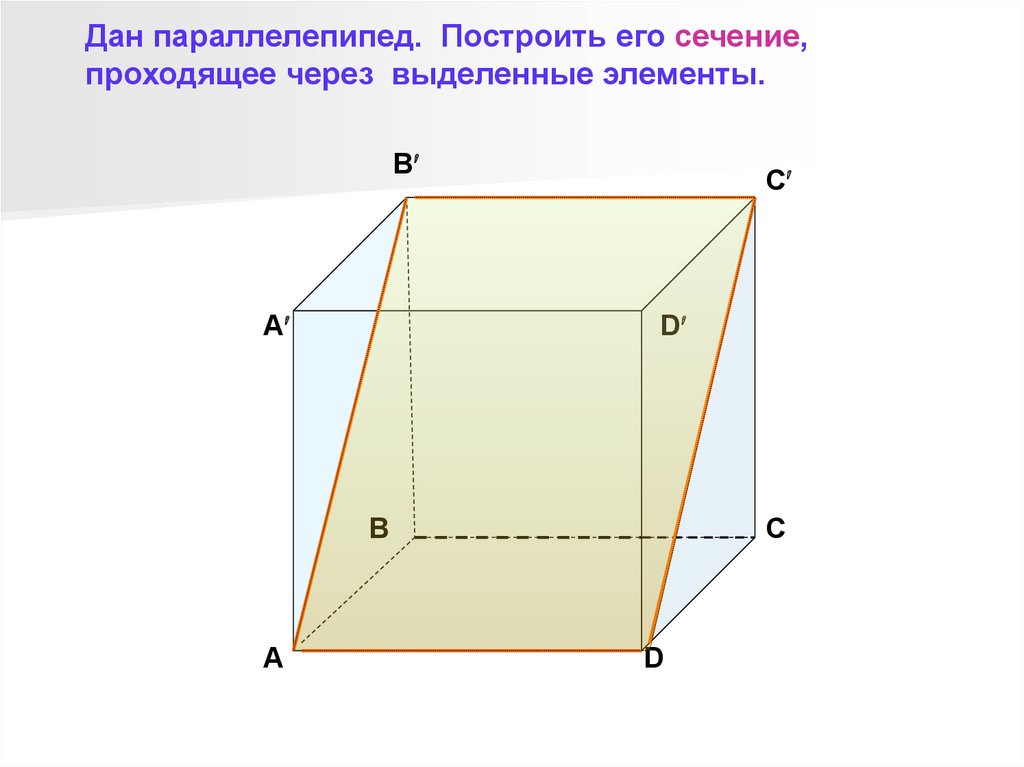
6.

Дан параллелепипед. Построить его сечение,
проходящее через выделенные элементы.
B
A
C
D
B
A
C
D

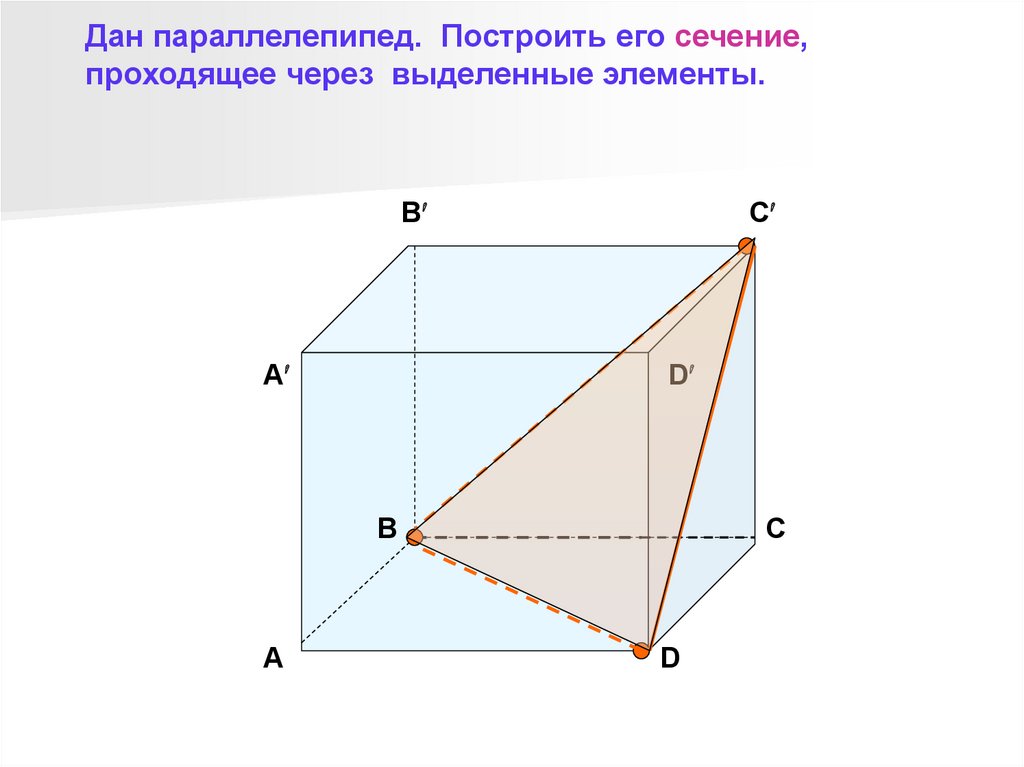
7.

Дан параллелепипед. Построить его сечение,
проходящее через выделенные элементы.
B
A
C
D
B
A
C
D

8. Вспомним!

Дан параллелепипед. Построить его сечение,
проходящее через выделенные элементы.
B
A
C
D
B
A
C
D

9.

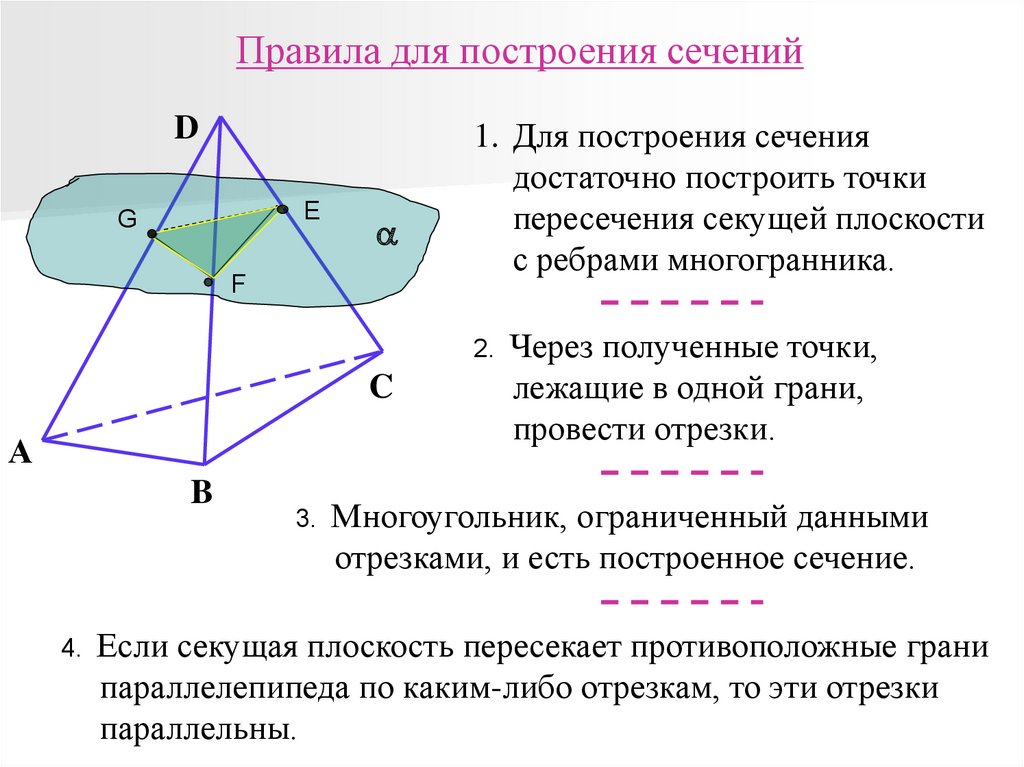
Правила для построения сечений
D
E
G
F
1. Для построения сечения
достаточно построить точки
пересечения секущей плоскости
с ребрами многогранника.
2.
C
А
B
4.
3.
Через полученные точки,
лежащие в одной грани,
провести отрезки.
Многоугольник, ограниченный данными
отрезками, и есть построенное сечение.
Если секущая плоскость пересекает противоположные грани
параллелепипеда по каким-либо отрезкам, то эти отрезки
параллельны.

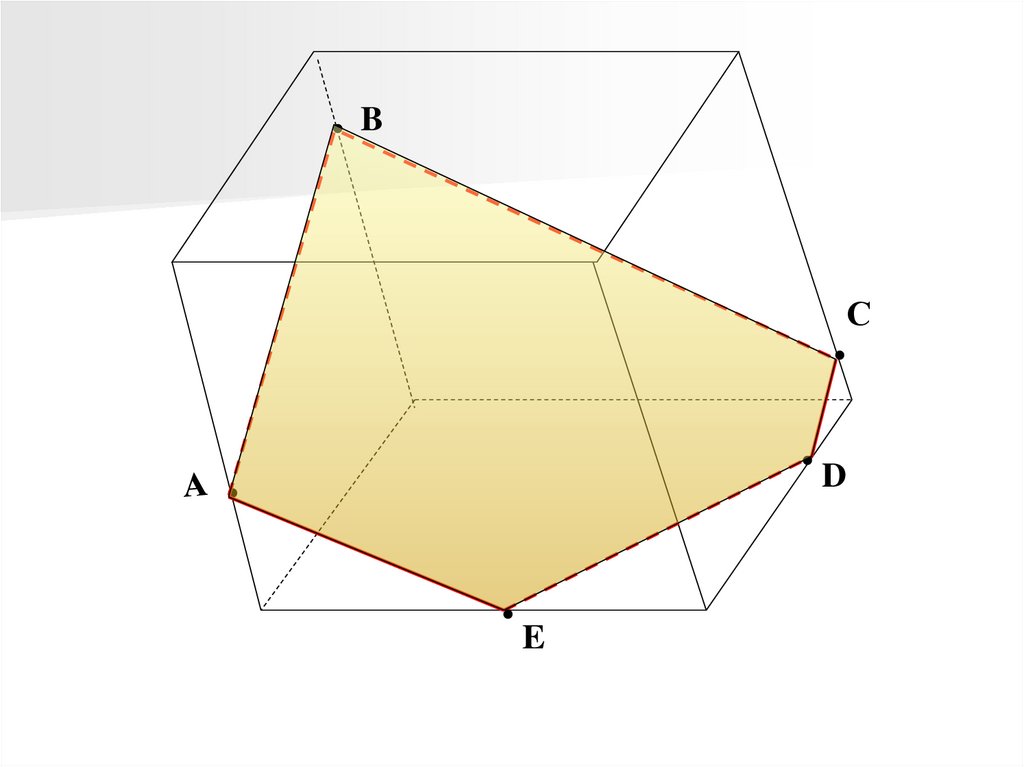
10.

B
С
D
E

11.

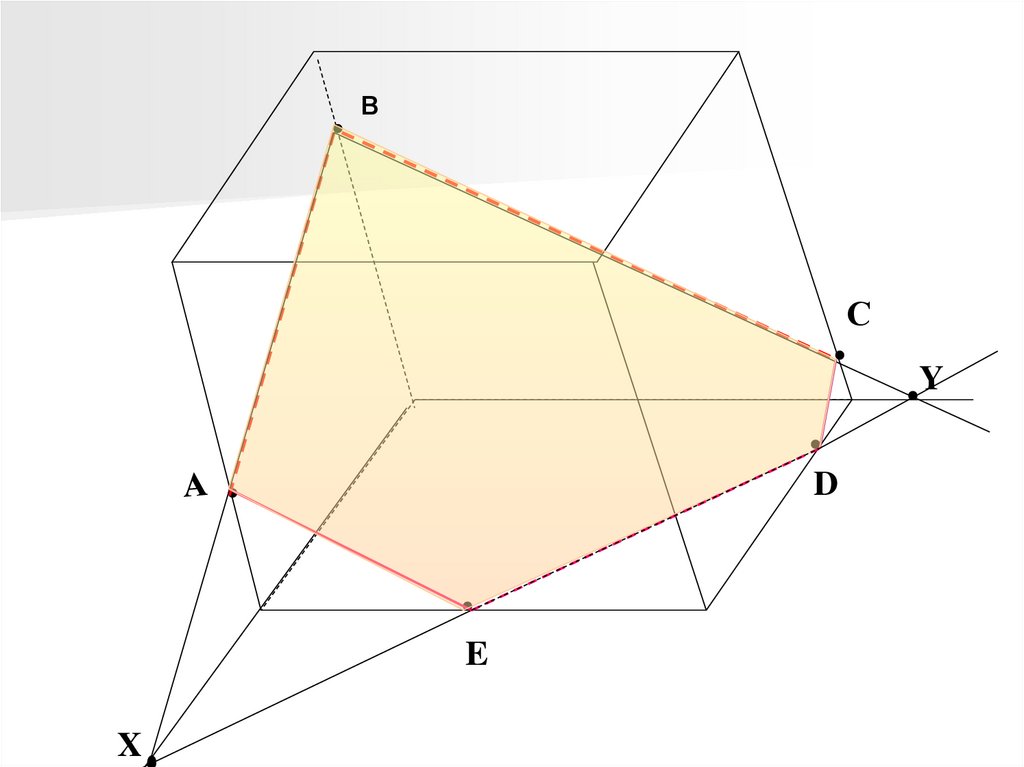
B
С
Y
D
E
X

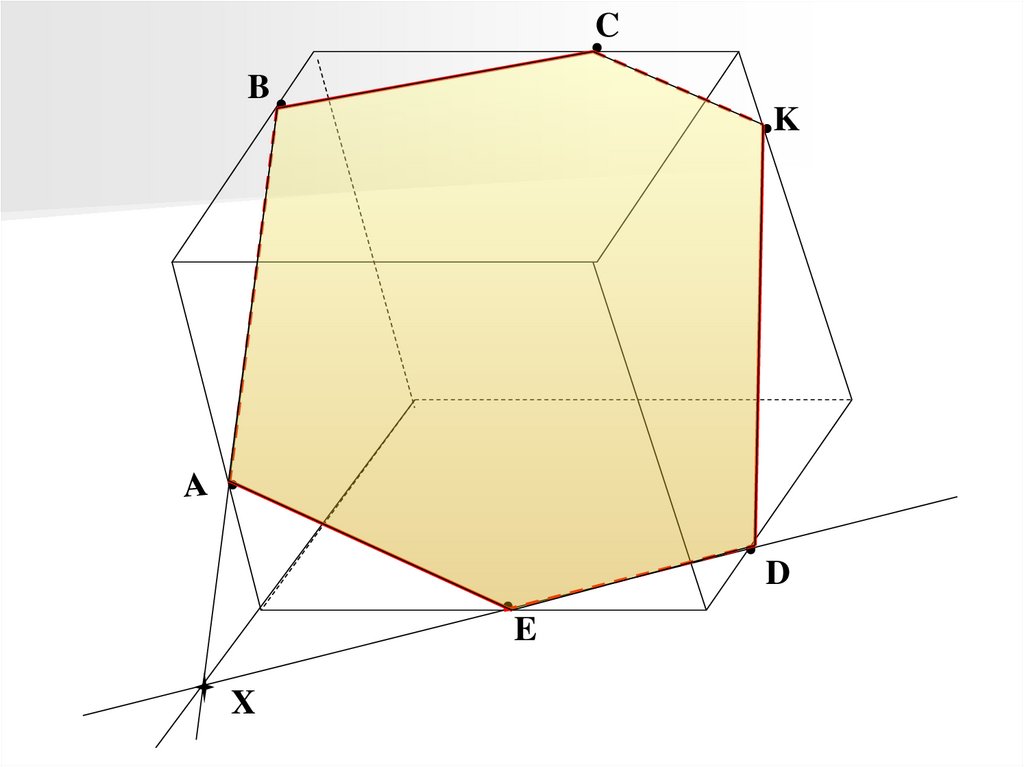
12.

C
B
K
D
E
X

13.

C
B

14.

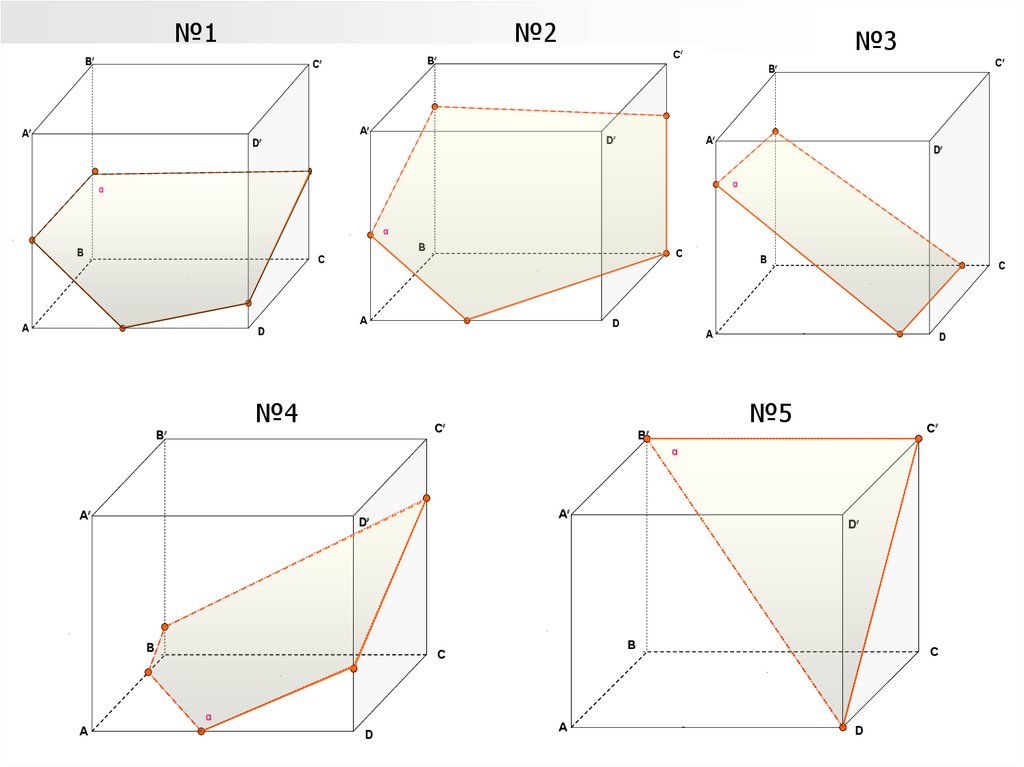
№1
№2
B
C
B
A
A
№3
C
B
C
D
D
A
D
α
α
α
B
B
C
C
A
A
B
C
D
D
A
№4
№5
C
B
D
C
B
α
A
A
D
B
D
B
C
C
α
A
D
A
D

15.

Домашнее задание
§4, п.14
Придумать и решить задачу на
построение сечения прямоугольного
параллелепипеда плоскостью,
проходящей через 3 данные точки.
Подготовить карточку-заготовку с
данной задачей.
№114 на «5»!