Использование информационных технологий на уроках математики

1. Использование информационных технологий на уроках математики как средство повышения познавательного интереса учащихся

Автор опыта
Петренко Л.И.

2.

…Урок- это зеркало общей и
педагогической культуры
учителя, мерило его
интеллектуального
богатства, показатель его
кругозоров и эрудиции
В. Сухомлинский

3.

● при изложении нового материала —
визуализация знаний (демонстрационно энциклопедические программы; программа
презентаций PowerPoint);
● закрепление изложенного материала
(тренинг — разнообразные обучающие
программы);
● система контроля и проверки (тестирование
с оцениванием, контролирующие программы);
● самостоятельная работа учащихся
(обучающие программы типа "Репетитор",
энциклопедии, развивающие программы);
● тренировка конкретных способностей
учащегося (внимание, память, мышление).

4. Задачи:

●Уточнить классификацию
образовательных средств ИКТ,
применяемую в образовательном
процессе в рамках данного предмета;
●Показать роль ИКТ в формировании
положительной мотивации у учащихся;
● Раскрыть многообразие форм
применения ИКТ на уроках математики.

5. Основные функциональные возможности мультимедийного урока:

• игровая форма познания;
• активное вмешательство в любой
процесс или явление, моделируемое в
ходе работы;
• наглядное отображение вмешательства
ребенка в процесс или явление;
• возможность для каждого ребенка
выбрать свой темп и режим работы.

6. Учебная информация готовится таким образом, чтобы решить следующие задачи:

• создать положительную мотивацию на
уроке;
• развивать смысловую догадку;
• открыть ребенку окно в мир знаний,
мир книг и открытий.

7. Методы и приемы:

анализ
сравнение
обобщение
классификация
проблемные, поисковые методы
игровой метод

8. Результаты работы с учащимися:

• Фиксируются мотивы предыдущих
достижений;
• Используется иллюстрированный
материал;
• Чередуются виды деятельности;
• Преодоление трудностей с помощью
учителя
• Организация поиска самих учащихся

9. Использование исследовательского метода при обучении математики

• Выделение и постановка проблемы ( выбор
темы);
Постановка целей и задач;
Определение объекта и предмета;
Выбор методов;
Сбор материала и обобщение полученных
данных;
Обсуждение результатов;
Формулирование выводов и оценка
полученных результатов.

10. Исследовательский навык, приобретенный в школе, поможет ученику:

• расширить знания и представления об окружающем мире,
увидеть бесконечность его познания;
• работать с различными источниками информации, осуществлять
выбор наиболее значимого содержания из имеющегося
информационного массива;
• сформировать научно – исследовательские навыки;
• реализовать личный творческий потенциал, самоутвердиться;
• воспитать не знатока – исполнителя, а Творца.

11. Цель применения компьютера на уроках математики:

Во- первых, решение практических задач:
- формирование прочных вычислительных умений
и навыков;
- овладение нормами математического языка;
- знание математических терминов;
Во- вторых, организация самостоятельной работы
учащихся;
В-третьих, применение информационных технологий
позволяет формировать ключевые компетенции
учащихся.

12. Работая с интерактивной доской, преподаватель сможет:

• - выполнить набор посредством виртуальной клавиатуры любого текста
задания в любом приложении и его демонстрацию в режиме реального
времени;
- провести полноценную работу с текстом с указанием связей и
взаимоотношений между словами;
- знакомство не только с тестовыми заданиями в режиме просмотра, но
и показательное тестирование отдельного ученика или группы
учеников для всей аудитории;
- сохранять сделанные записи и пометки, исправления в документе и
файле. Записать все действия на доске в единый файл конспекта
урока;
- интерактивная доска дает возможность на уроках использовать
тезисы, таблицы, видео- и справочные материалы;
- на видеоматериале можно организовать речевую ситуацию, обучать
постановке вопроса, составлению высказывания, организации диалога.

13. Результаты работы:

• повысился интерес и активность
учащихся на уроке;
• накоплена большая методическая база
дидактических материалов в
электронном виде;
• созданы циклы уроков с
использованием ИКТ по различным
темам.

14. Применение мультимедийных технологий

15. Параллельные прямые

Признаки параллельности прямых
Основные понятия
Свойства параллельных прямых
Комбинированные задачи

16. Признаки параллельности прямых

1
2
3
4
5
6

17. Свойства параллельности прямых

7
1
2
6
3
4
5

18. Основные понятия

1
2
3

19. Комбинированные задачи

Устные задачи
Задачи 1 уровня сложности
Задачи 2 уровня сложности
Задачи 3 уровня сложности

20.

Устно. Признаки параллельности прямых.
№1
Доказать: а‫ ׀׀‬в
а
32°
в
32°
с
№2
Доказать: а‫ ׀׀‬р
в
а
48°
132°
р

21.

№3
Доказать: р ‫ ׀׀‬к
с
47°
р
133°
к
№4
а
Дано: а ‫ ׀׀‬с
Доказать: в ‫ ׀׀‬с
с
в
р

22.

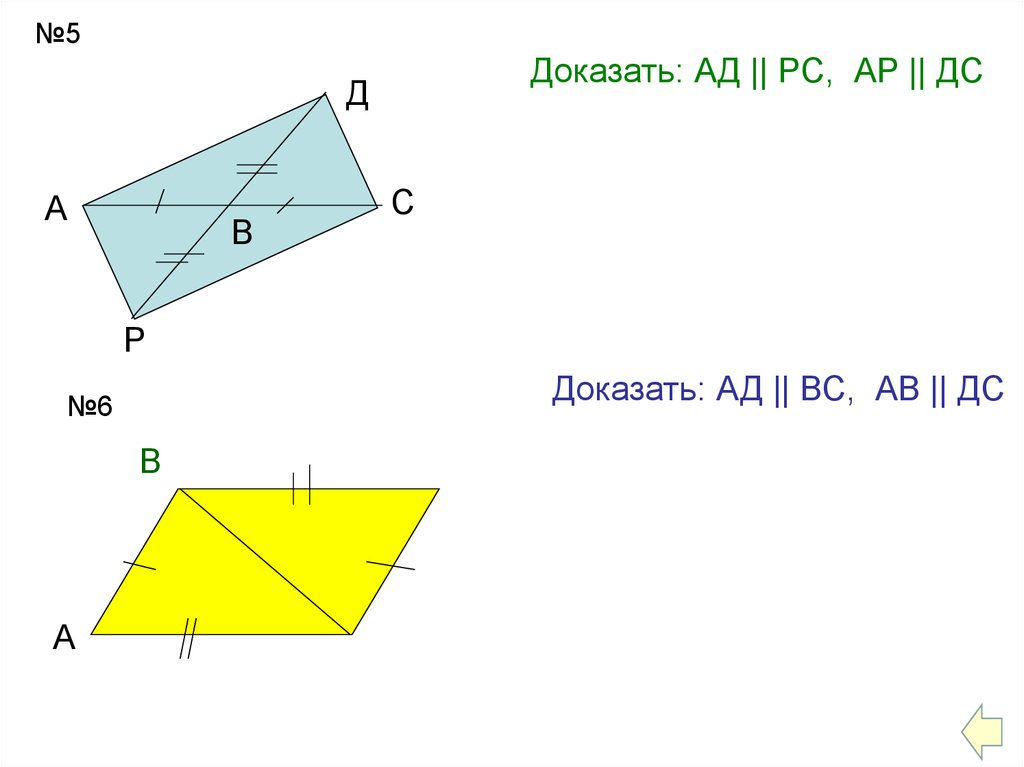
№5
Доказать: АД || РС, АР || ДС
Д
А
В
С
Р
Доказать: АД || ВС, АВ || ДС
№6
В
А

23.

№7
В
Доказать: ВК || РС, АД || ВС
С
Д
А
К
№8
Р
Доказать: АВ || ДР
В
А
С
Д
Р

24.

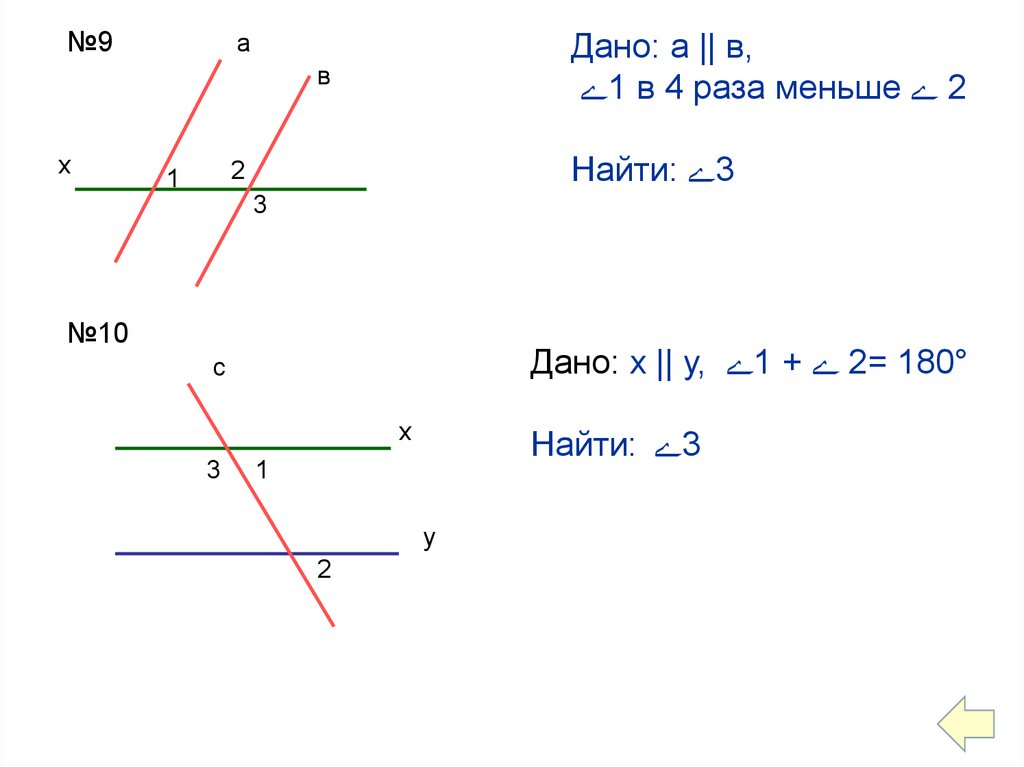
№9
Дано: а || в,
‫ ‬1 в 4 раза меньше ‫ ‬2
а
в
х
Найти: ‫ ‬3
2
1
3
№10
Дано: х || у, ‫ ‬1 + ‫ ‬2= 180°
с
х
3
Найти: ‫ ‬3
1
у
2

25.

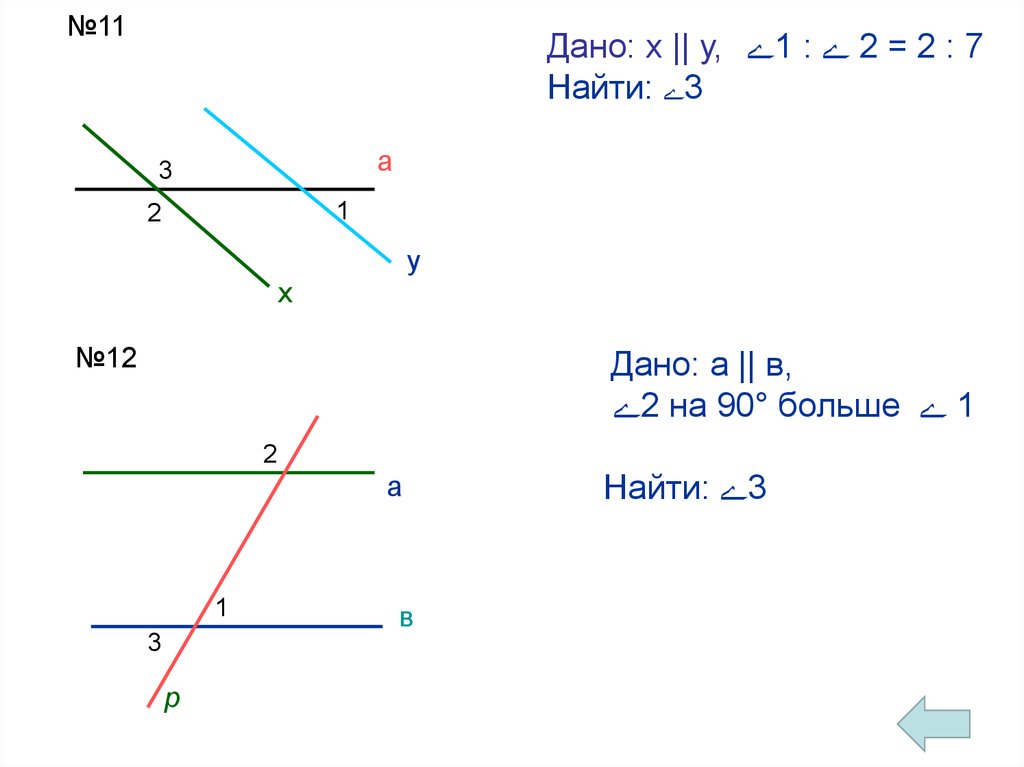
№11
Дано: х || у, ‫ ‬1 : ‫ ‬2 = 2 : 7
Найти: ‫ ‬3
а
3
1
2
у
х
№12
Дано: а || в,
‫ ‬2 на 90° больше ‫ ‬1
2
а
1
3
р
в
Найти: ‫ ‬3

26.

№1
Параллельны ли прямые а и в?
а
39°
в
141°
№2
Е
О – середина отрезков ЕМ и КР.
Доказать, что ЕР || КМ
Р
О
К
М

27.

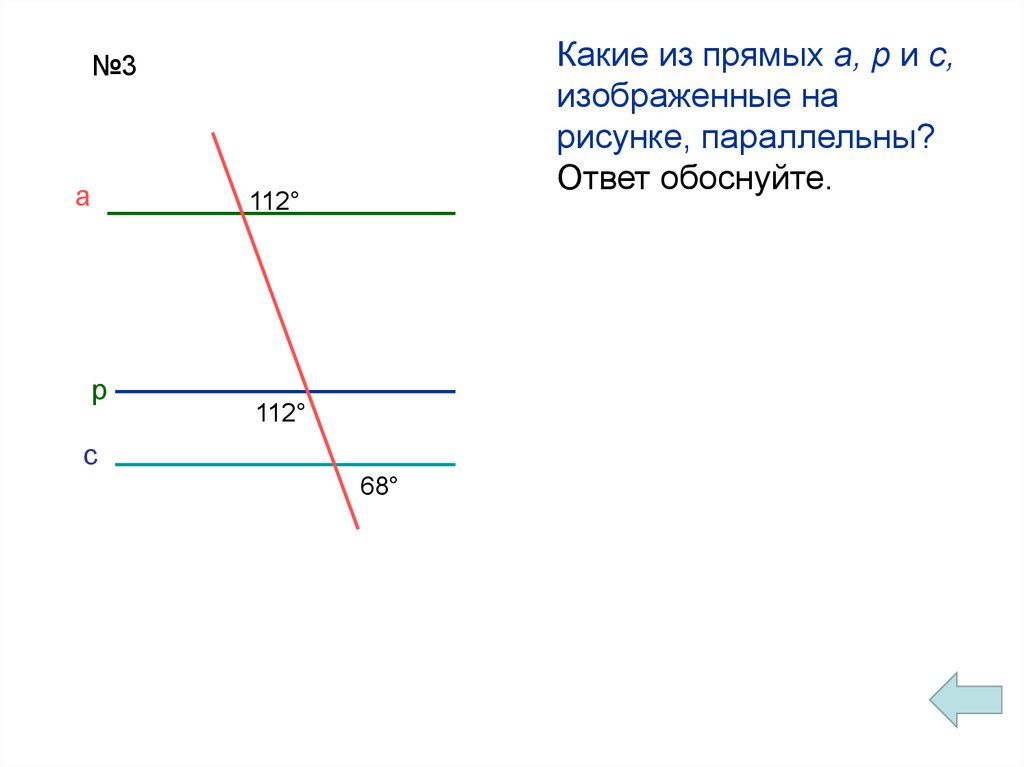
Какие из прямых а, р и с,
изображенные на
рисунке, параллельны?
Ответ обоснуйте.
№3
а
112°
р
112°
с
68°

28.

№4
Доказать, что МЕ || ОР
Е
2
М
1
О
Р

29.

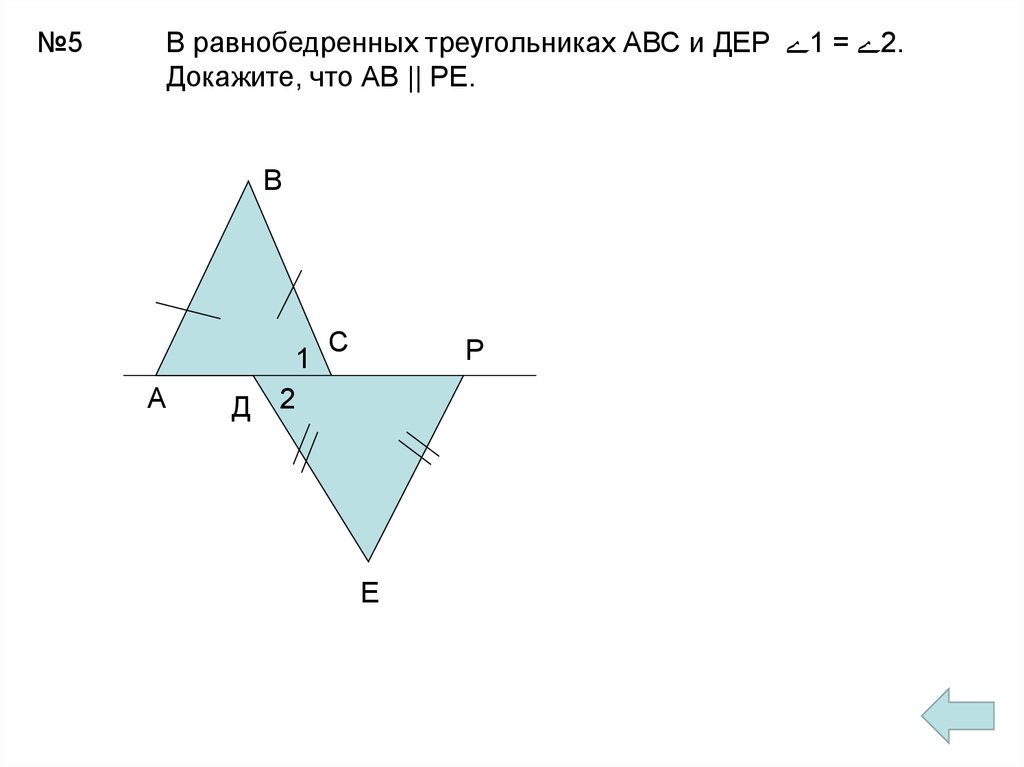
№5
В равнобедренных треугольниках АВС и ДЕР ‫ ‬1 = ‫ ‬2.
Докажите, что АВ || РЕ.
В
1
А
Д
С
Р
2
Е

30.

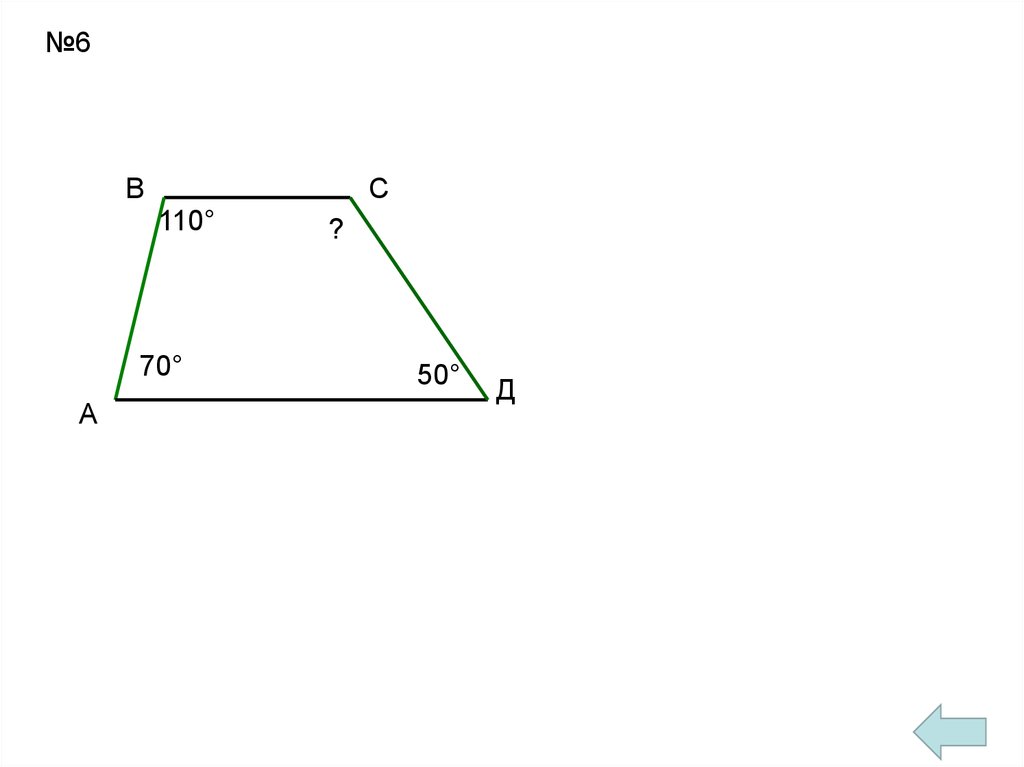
№6
В
С
110°
70°
А
?
50°
Д

31.

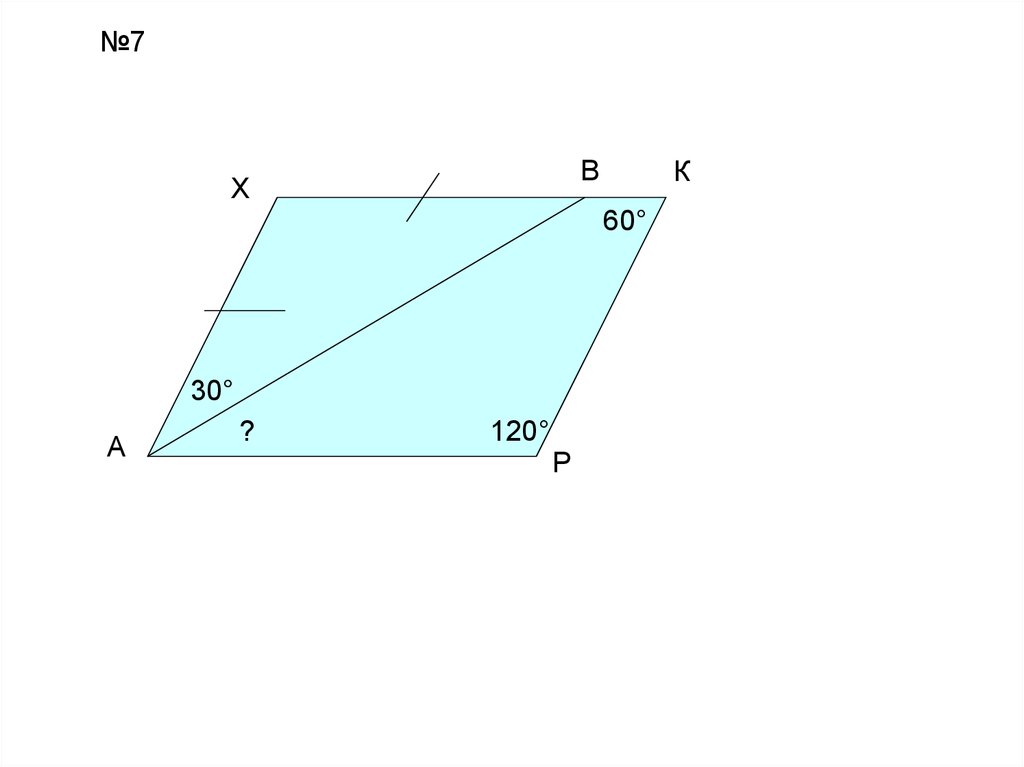
№7
В
Х
К
60°
30°
А
?
120°
Р

32.

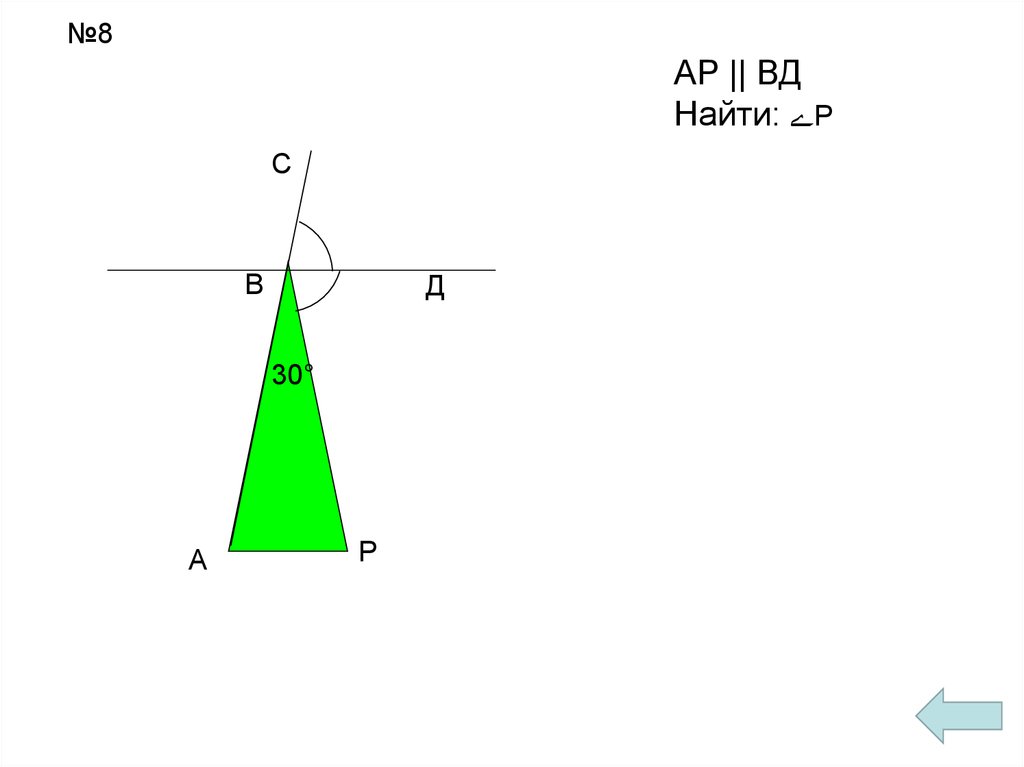
№8
АР || ВД
Найти: ‫ ‬Р
С
В
Д
30°
А
Р

33.

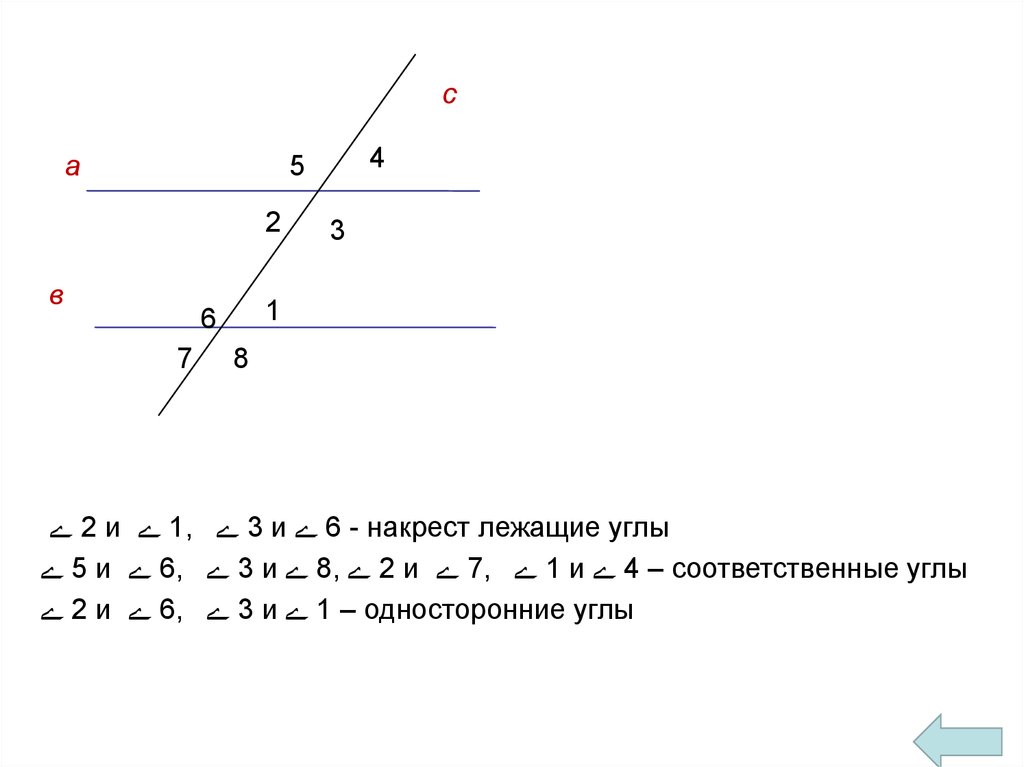
с
а
4
5
2
в
1
6
7
3
8
‫ ‬2 и ‫ ‬1, ‫ ‬3 и ‫ ‬6 - накрест лежащие углы
‫ ‬5 и ‫ ‬6, ‫ ‬3 и ‫ ‬8, ‫ ‬2 и ‫ ‬7, ‫ ‬1 и ‫ ‬4 – соответственные углы
‫ ‬2 и ‫ ‬6, ‫ ‬3 и ‫ ‬1 – односторонние углы

34.

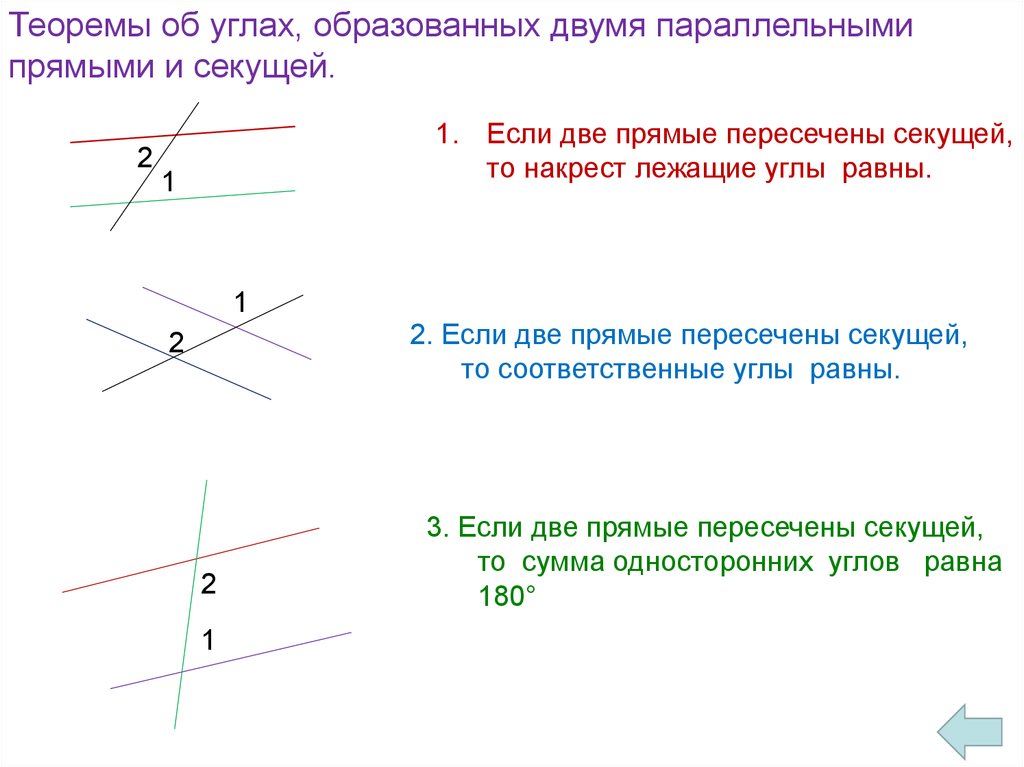
Теоремы об углах, образованных двумя параллельными
прямыми и секущей.
2
1. Если две прямые пересечены секущей,
то накрест лежащие углы равны.
1
1
2. Если две прямые пересечены секущей,
то соответственные углы равны.
2
2
1
3. Если две прямые пересечены секущей,
то сумма односторонних углов равна
180°

35.

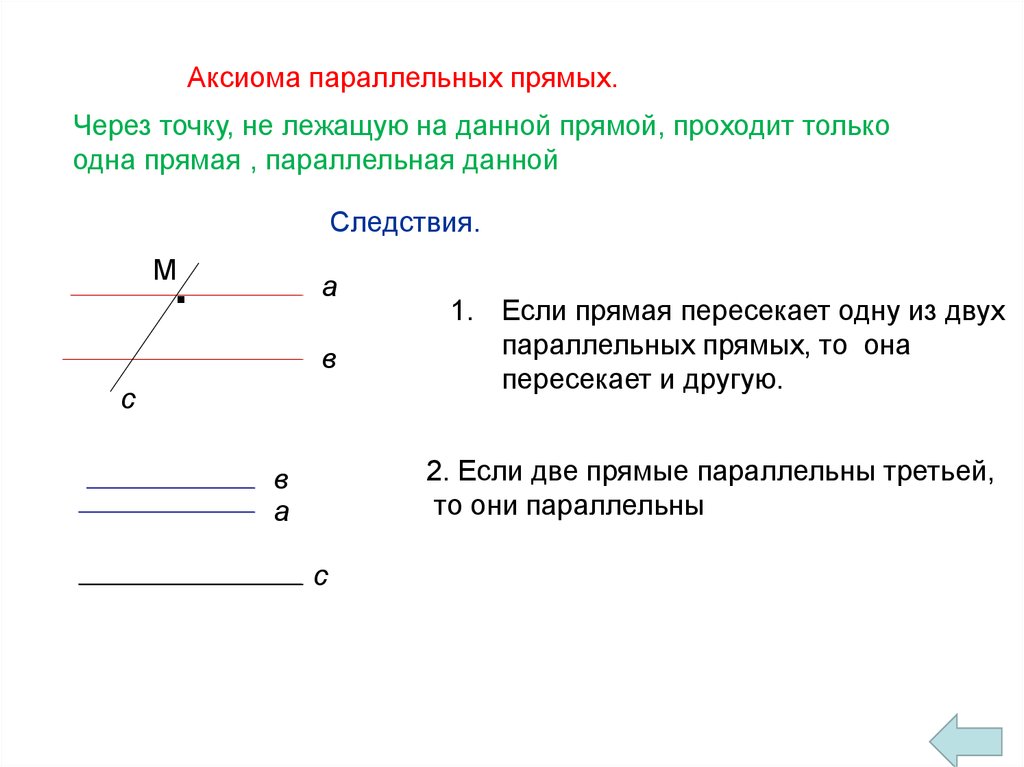
Аксиома параллельных прямых.
Через точку, не лежащую на данной прямой, проходит только
одна прямая , параллельная данной
Следствия.
М
·
а
в
с
1. Если прямая пересекает одну из двух
параллельных прямых, то она
пересекает и другую.
2. Если две прямые параллельны третьей,
то они параллельны
в
а
с

36.

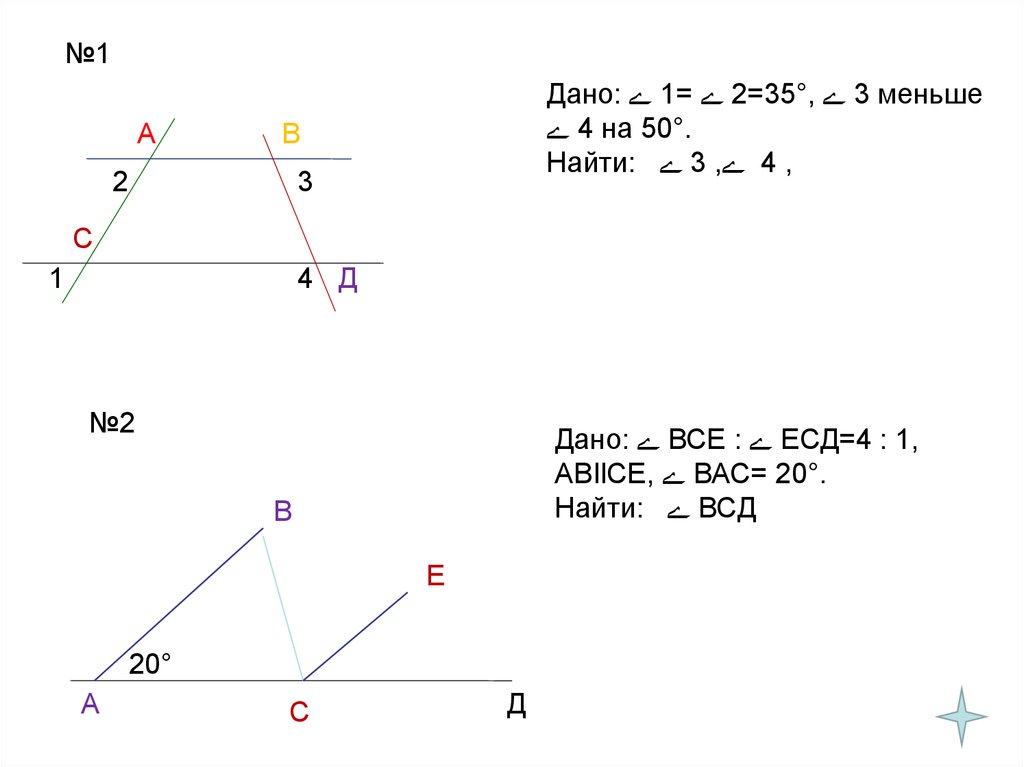
№1
А
Дано: ‫ ‬1= ‫ ‬2=35°, ‫ ‬3 меньше
‫ ‬4 на 50°.
Найти: ‫ ‬3 ,‫ ‬4 ,
В
2
3
С
4 Д
1
№2
Дано: ‫ ‬ВСЕ : ‫ ‬ЕСД=4 : 1,
АВIlСЕ, ‫ ‬ВАС= 20°.
Найти: ‫ ‬ВСД
В
Е
20°
А
С
Д

37.

Аксиома параллельных прямых.
Через точку, не лежащую на данной прямой, проходит только
одна прямая , параллельная данной
Следствия.
М
·
а
в
с
1. Если прямая пересекает одну из двух
параллельных прямых, то она
пересекает и другую.
2. Если две прямые параллельны третьей,
то они параллельны
в
а
с

38.

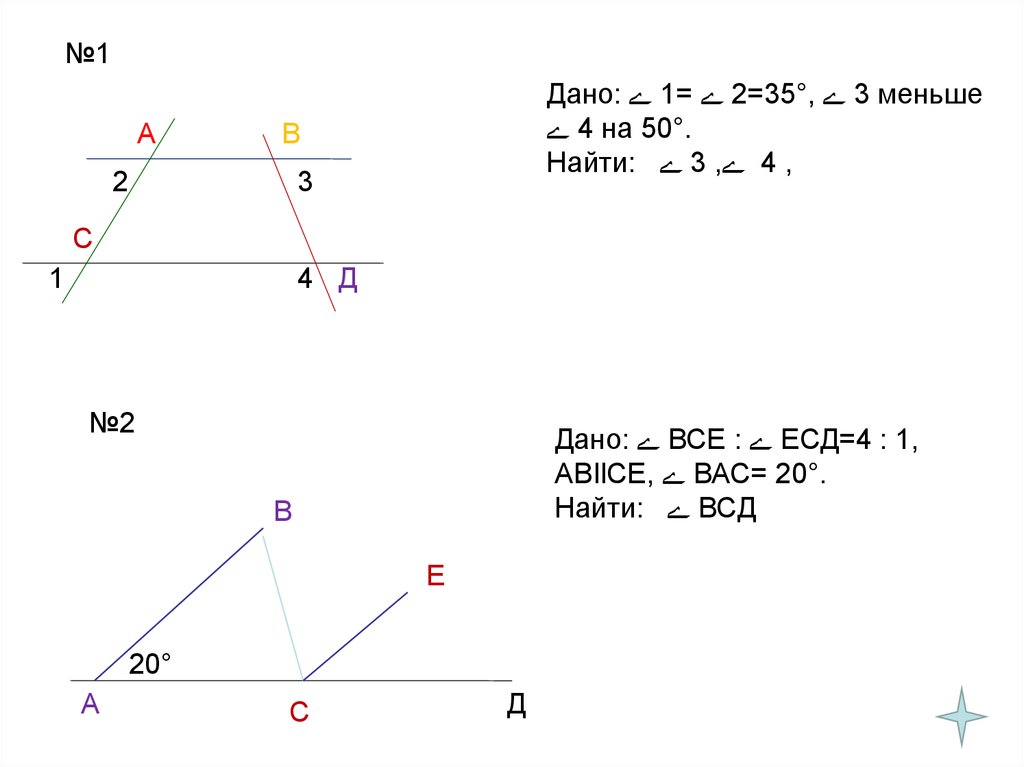
№1
А
Дано: ‫ ‬1= ‫ ‬2=35°, ‫ ‬3 меньше
‫ ‬4 на 50°.
Найти: ‫ ‬3 ,‫ ‬4 ,
В
2
3
С
4 Д
1
№2
Дано: ‫ ‬ВСЕ : ‫ ‬ЕСД=4 : 1,
АВIlСЕ, ‫ ‬ВАС= 20°.
Найти: ‫ ‬ВСД
В
Е
20°
А
С
Д

39.

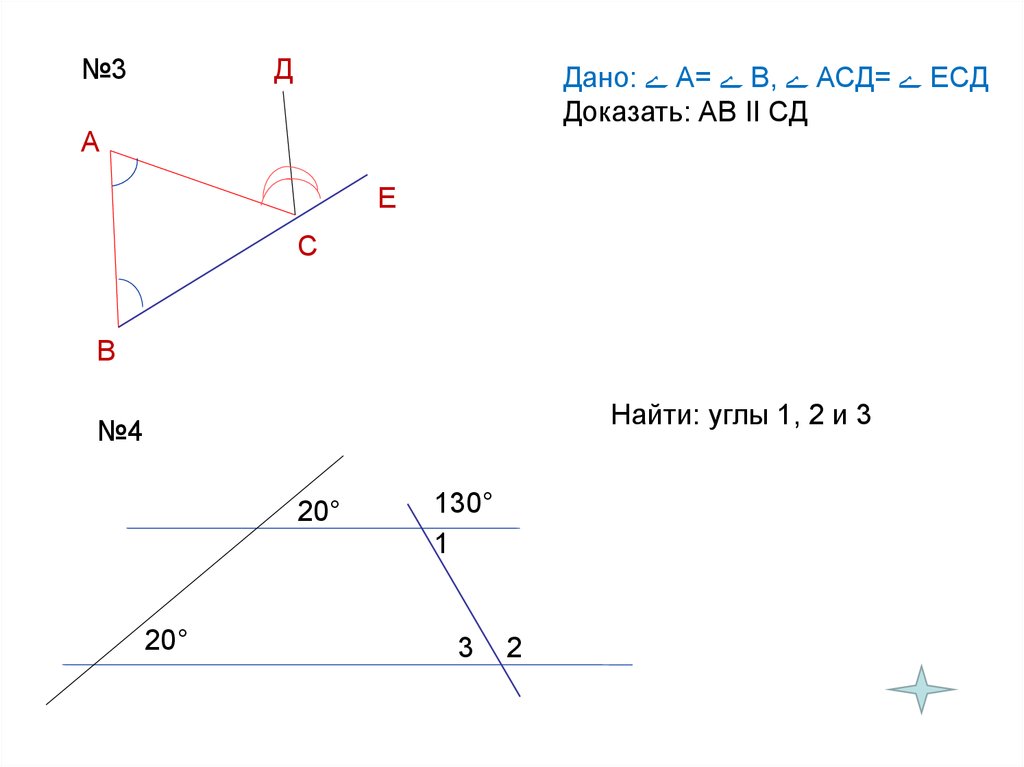
№3
Д
Дано: ‫ ‬А= ‫ ‬В, ‫ ‬АСД= ‫ ‬ЕСД
Доказать: АВ II СД
А
Е
С
В
Найти: углы 1, 2 и 3
№4
20°
20°
130°
1
3
2

40.

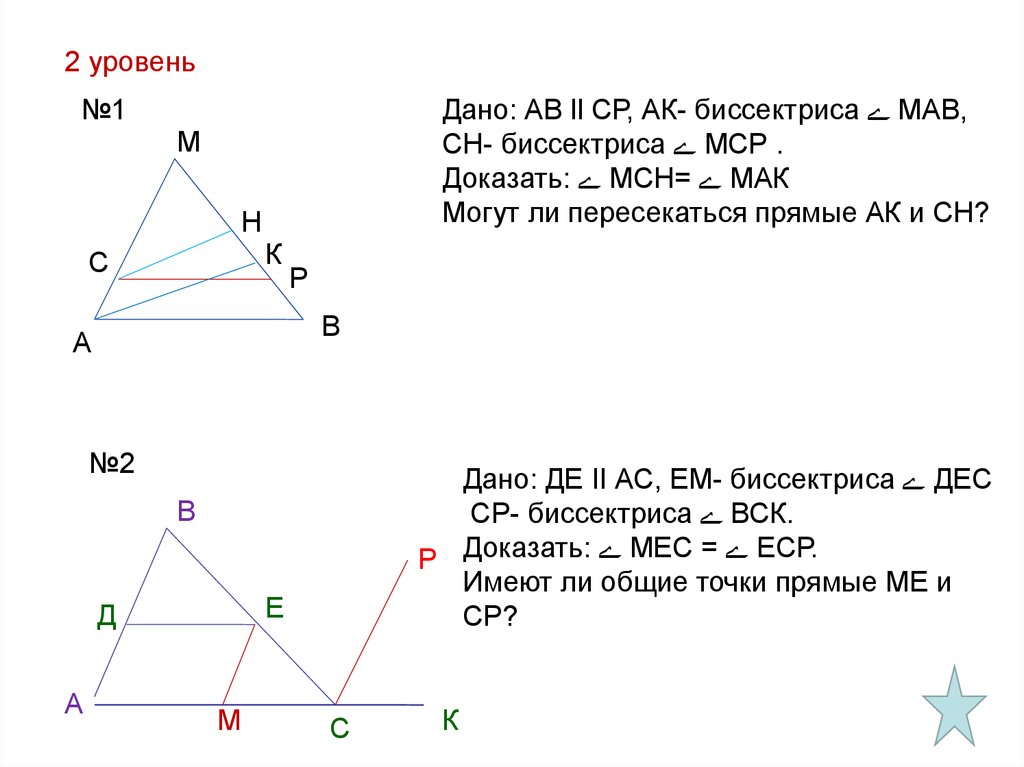
2 уровень
№1
Дано: АВ ll СР, АК- биссектриса ‫ ‬МАВ,
СН- биссектриса ‫ ‬МСР .
Доказать: ‫ ‬МСН= ‫ ‬МАК
Могут ли пересекаться прямые АК и СН?
М
Н
К
С
Р
В
А
№2
Дано: ДЕ II АС, ЕМ- биссектриса ‫ ‬ДЕС
СР- биссектриса ‫ ‬ВСК.
Р Доказать: ‫ ‬МЕС = ‫ ‬ЕСР.
Имеют ли общие точки прямые МЕ и
СР?
В
Е
Д
А
М
С
К

41.

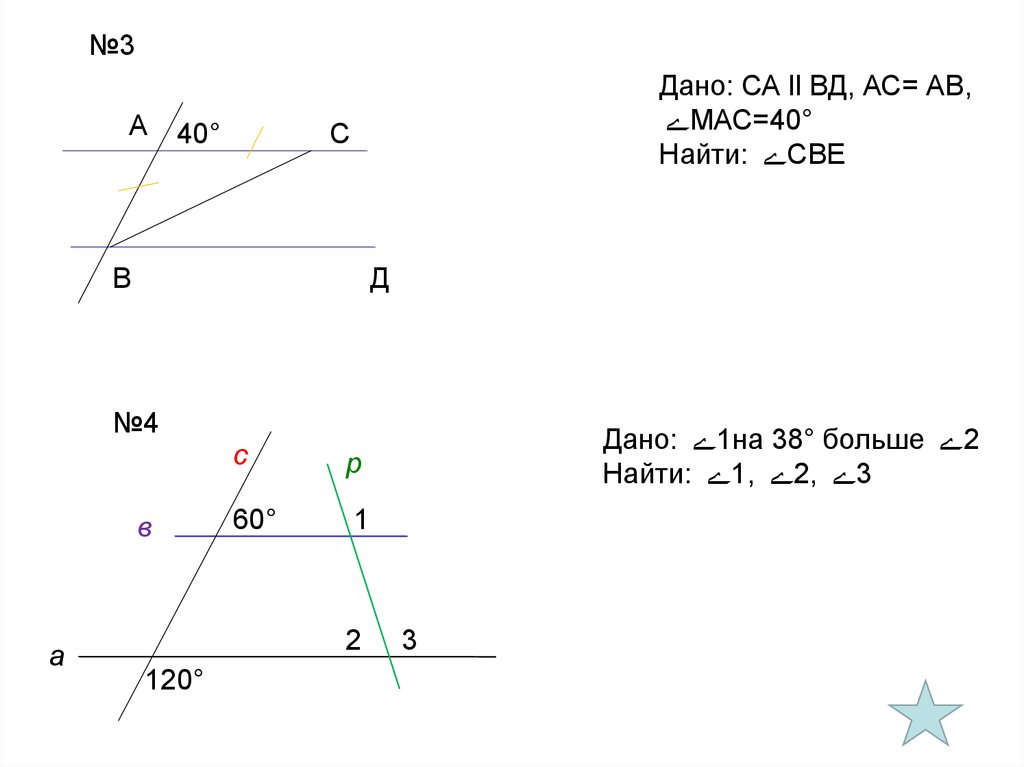
№3
А
Дано: СА ll ВД, АС= АВ,
‫ ‬МАС=40°
Найти: ‫ ‬СВЕ
С
40°
В
Д
№4
в
а
с
р
60°
1
2
120°
Дано: ‫ ‬1на 38° больше ‫ ‬2
Найти: ‫ ‬1, ‫ ‬2, ‫ ‬3
3

42. №5 Отрезки СД и АВ пересекаются в точке О так, что ОА=ОВ, АС ll ДВ. Докажите, что треугольники АОС и ДОВ равны.

№6
В четырехугольнике АВСД ВС=АД и ВС ll ДА.
Докажите, что треугольники АВС и ДАС равны.

43.

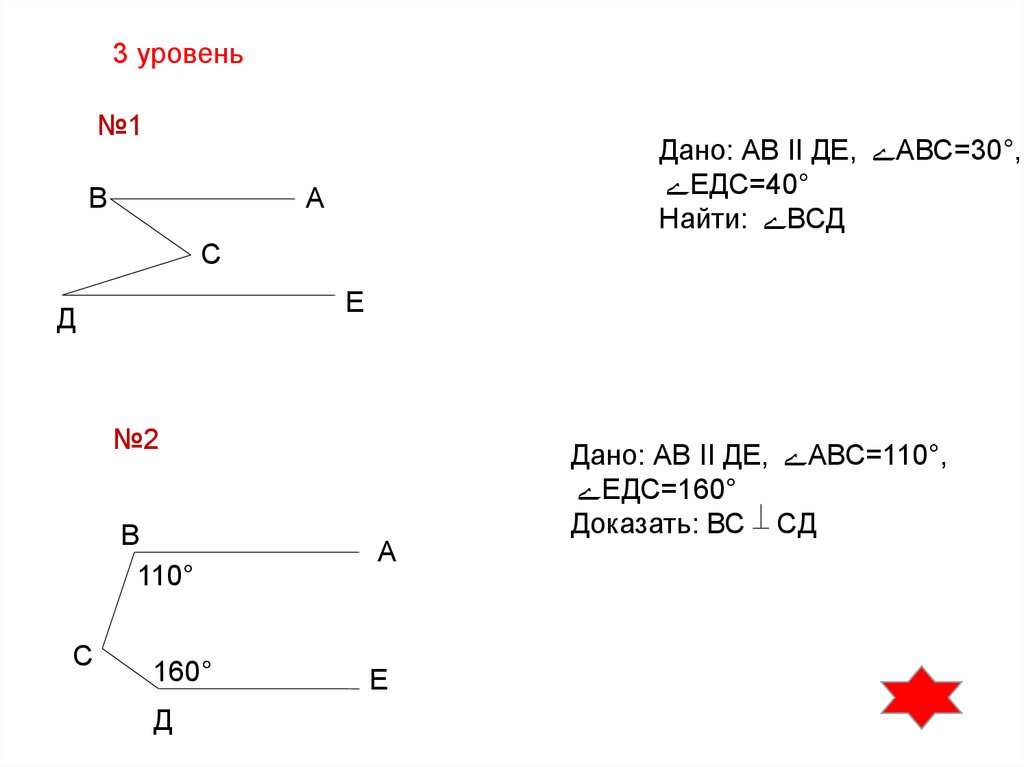
3 уровень
№1
В
Дано: АВ II ДЕ, ‫ ‬АВС=30°,
‫ ‬ЕДС=40°
Найти: ‫ ‬ВСД
А
С
Е
Д
№2
В
110°
С
160°
Д
А
Е
Дано: АВ II ДЕ, ‫ ‬АВС=110°,
‫ ‬ЕДС=160°
Доказать: ВС СД

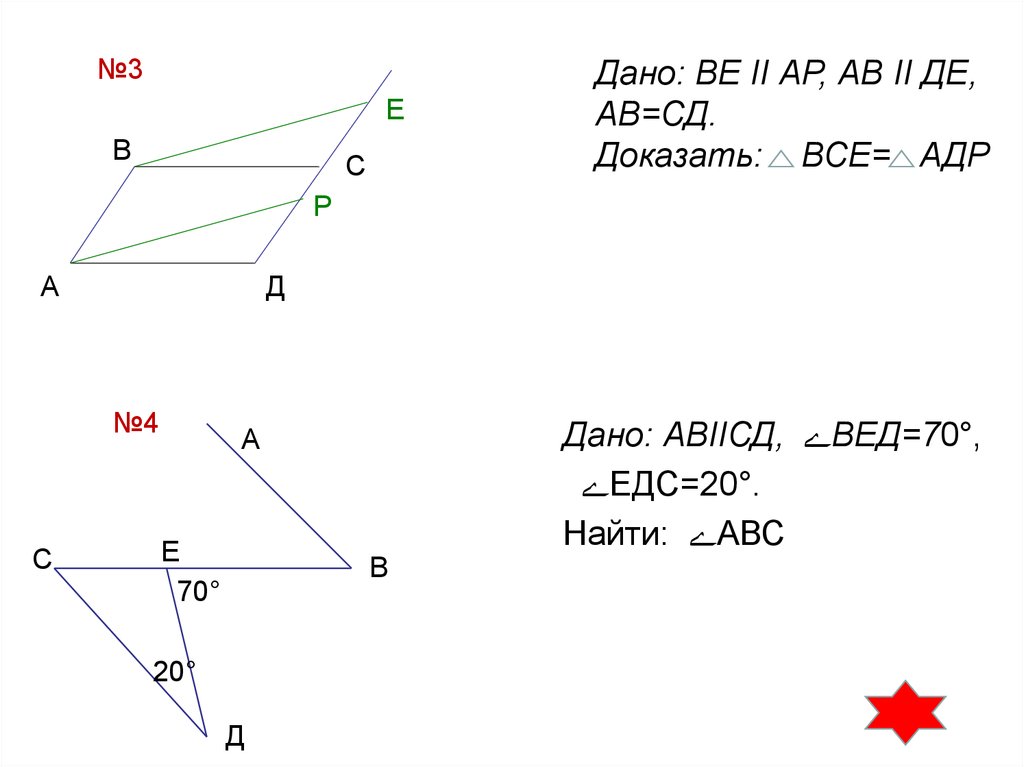
44. Дано: ВЕ II АР, АВ II ДЕ, АВ=СД. Доказать: ВСЕ= АДР

№3
Е
В
С
Дано: ВЕ II АР, АВ II ДЕ,
АВ=СД.
Доказать: ВСЕ= АДР
Р
А
Д
№4
С
А
Е
70°
В
20°
Д
Дано: АВIIСД, ‫ ‬ВЕД=70°,
‫ ‬ЕДС=20°.
Найти: ‫ ‬АВС

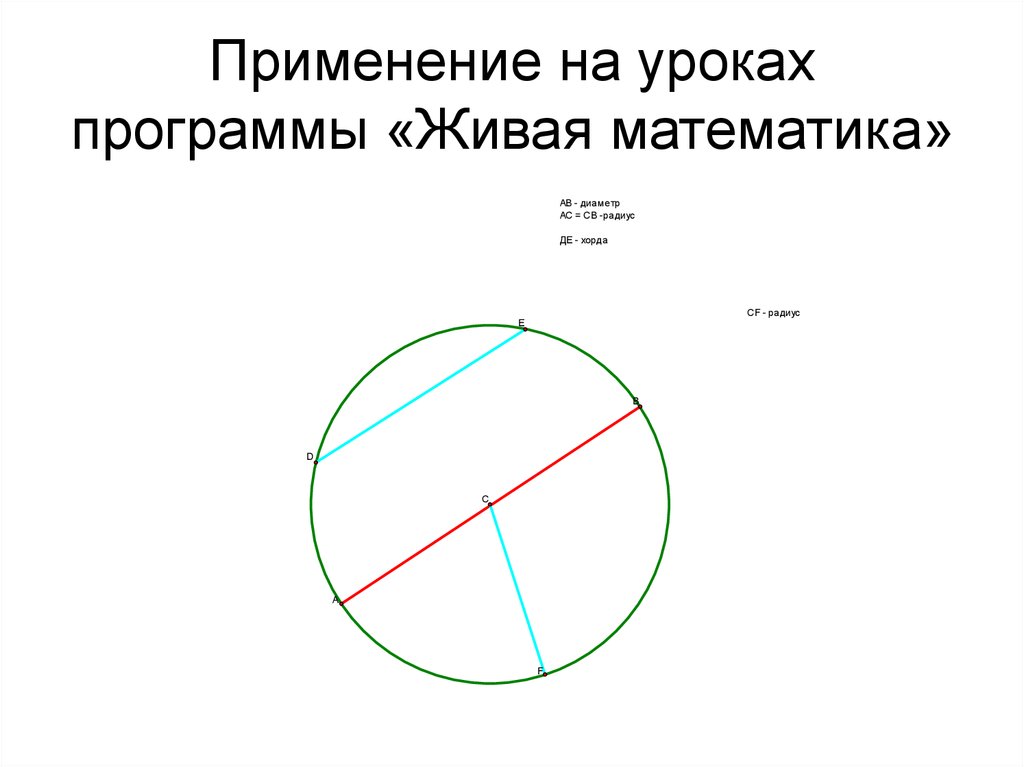
45. Применение на уроках программы «Живая математика»

АВ - диаметр
АС = СВ -радиус
ДЕ - хорда
СF - радиус
E
B
D
C
A
F

46.

f x = x2+1
g x =
2
x
10
8
6
4
2
-15
-10
-5
5
-2
-4
-6
-8
-10
-12
10
15

47.

f x = x2
g x = x+2 2
h x = x+2 2-4
10
8
6
4
2
-15
-10
-5
5
-2
-4
-6
-8
-10
-12
10
15

48. Работа с интерактивной доской

49.

Найди ошибку!
(3х+7)*2-3=17
(3х+7)*2=17-3,
(3х+7)*2=14
3х+7=14:2
3х=7-7.
Х=0

50.

Задача на логическое мышление.
Цифры 1,2,3,4,5,6,7,8,9 расставьте в клетки так, чтобы
равенства были верными.
*
=
=
*