Уравнение касательной к графику функции

1.

2. 1. Записать уравнение касательной к графику функции

3. 2.Найти f’(x)

4. 3.Найти значение производной функции f (x)= sin  х в точке х0=3/2

А) – ;
В) 1;
Б) ;
Г) -1;

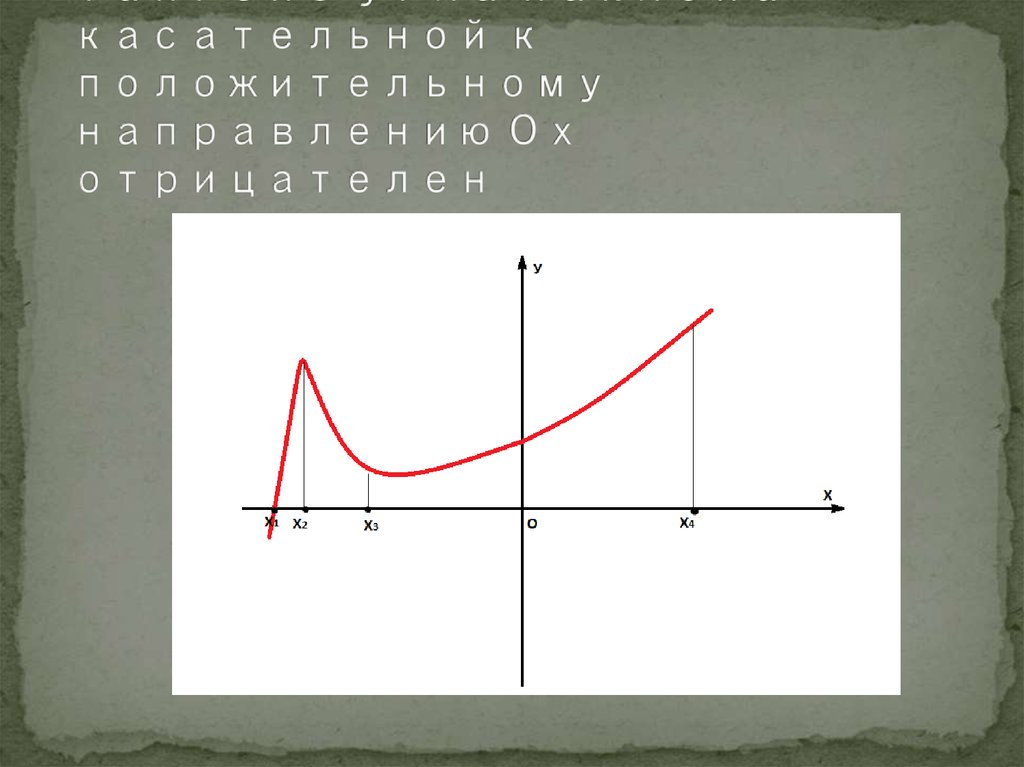
5. 4.Найти абсциссу точки графика функции, в которой тангенс угла наклона касательной к положительному направлению Ох отрицателен

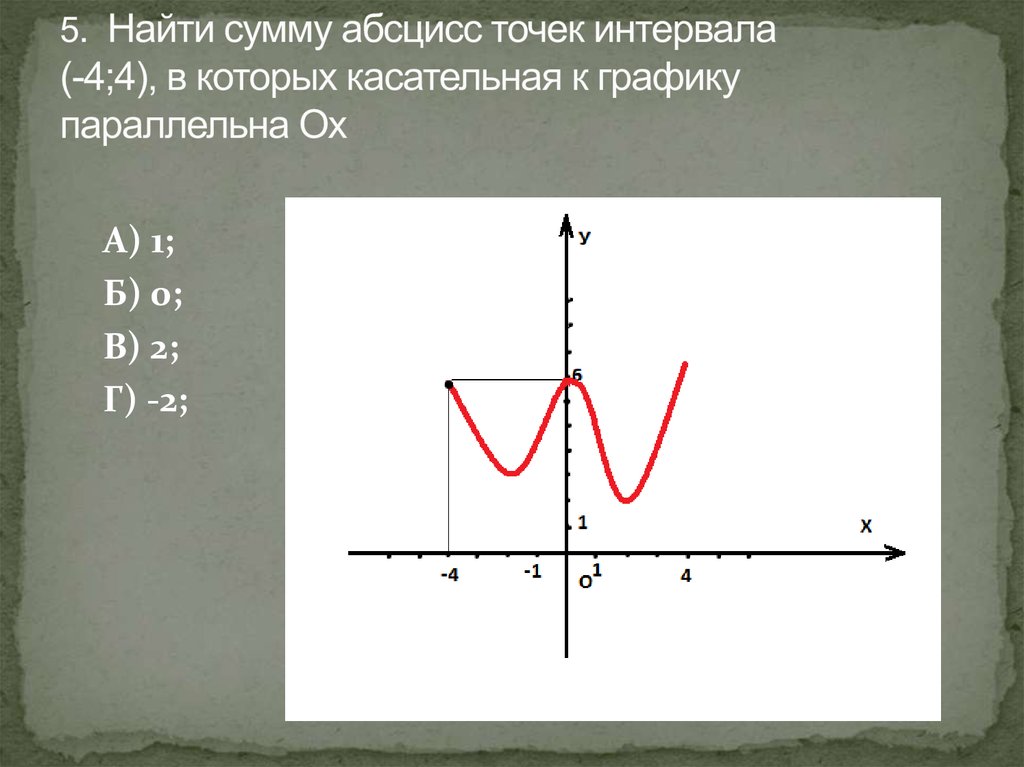
6. 5. Найти сумму абсцисс точек интервала (-4;4), в которых касательная к графику параллельна Ох

А) 1;
Б) 0;
В) 2;
Г) -2;

7. Проверка

1.
у – у0 = k (х –х0),
где у0=F (x0), k = f ‘ (x0)
2а. 4х – 5
2б. (9 5 х4)/5
2в. 19 / (7-х)2
3. -
4. х3
5. 0

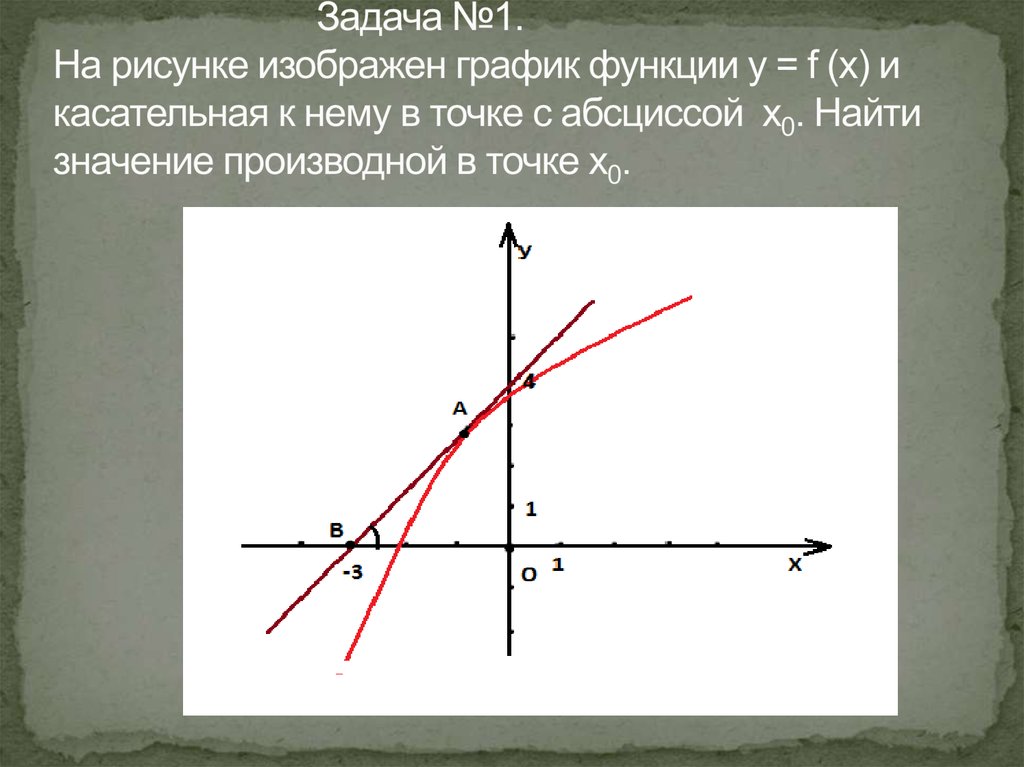
8. Задача №1. На рисунке изображен график функции у = f (x) и касательная к нему в точке с абсциссой х0. Найти значение

9. Решение задачи №1.

f ‘ (x) = tg , - угол между этой касательной и
положительным направлением оси Ох.
= АВО
Из АВО: tg АВО = АО/ВО, АО=4, ВО=3,
tg АВО=4/3.
f ‘ (x) = 4/3
Ответ:4/3

10. Задача №2.

Напишите уравнение касательной к графику
функции f(x) = (х8-1)/(х4+1) параллельной
прямой у = -32x+7.
Ответ:
у = -32х-49

11. Задача №3.

На параболе у = х2-2х-8 найти точку М, в
которой касательная к ней параллельна
прямой 4х+у+4=0.
Ответ: М (-1;-5)

12. Задача №4.

Найти координаты точки, в которой
касательная к параболе у=х2-х-12 образует
с осью Ох угол 450?