Похожие презентации:
Устный счет. Арифметический корень натуральной степени
1.
Подготовили: Горбункова АняПшикова Маша
Юсупова Юля
2. Арифметический корень натуральной степени
3.
1. Возвести в квадрат числа:0;
3 2
7; ; 1
8 3
; 0,2; 0,6; -1,1; 0,08.
4.
2. Представить в видеквадрата числа:
49
6
4
1; 16 ; 0,0001; 42 ; 1,5 .
5.
3. Представить в виде кубачисла:
8
6
9
3
; 0,001; 2 ; 2 ; 2 .
27
6.
4. Упростить выражения:( 2 2) ; ( 3 2 ) ; 3 2 2.
2
2
7. Степенная функция
8.
1. Какова область определения функции y= f(x)?
2. Каково множество значений функции y= f
(x)?
3. Является ли функция четной? Нечетной?
4. На каких промежутках функция возрастает?
Убывает?
9.
5. При каких значениях хфункция принимает
значение, равное нулю?
Положительные значения?
Отрицательные значения?
6. Каково значение функции
при х=0? Х=2?
10. Иррациональные уравнения
11.
1.Представьте в виде степеничисла a>0:
5
1
2
2)а
1)а а а ;
3
1
а3 а
3)
;
2
а3
3 2
:а ;
2
4)(а ) ;
3
1
6 3
2
5)(а ) а .
3
12.
2. Определить, какое из двух уравненийявляется следствием другого:
1) х 9 и х 3;
2
2)х-5=0 и х(х-5)=0;
х 3х
3)
0и
х
2
х 7
4)
0
х
х 3х 0;
2
и х 7 0.
13. Показательная функция, ее свойства и график
14.
1. Представьте в виде степени числаа>0:
1
2
5
1)а а а ;
3
3)
4) а
3
3
1
3
а *а
а
;
2)а
2
3
3 2
:а ;
2
;
5) а
1
6 3
2
*а .
15.
2. Найти значение выражения:2
1)
7
2
8
7
6
;
2
4
5
2) * 2 * 3 .
3
16.
3. Сравнить с единицей:3
5
1)1,3 ; 2)0,7 .
17.
4. Сравнить:1
2
1
3
1)0,9 и0,9 ; 2) и .
7
6
18. Показательные уравнения
19.
1. Выяснить, возрастающей илиубывающей является функция:
1) у 7,3 ; 2) у 0,6 ;
х
х
х
х
3) у 0,2 ;
5
4) у .
3
20.
2. Записать данную функцию ввиде показательной:
1) у 3 * 4 ;
х
3) у 5 ;
2х
х
х
6
2) у х ;
2
3х
4
4) у 5 х .
2
21.
3. Сравнить:5
7 7
1) и
4 4
3) 1 и
2
5 ,1
2
; 2)
3
8
7
3
и ;
2
1
3
1
2
3
1 ; 4) и 2 3 ;
2
22.
4. Представить числа:1
1)1;32; ;0,25 в виде степени числа 2;
64
1
1
2) ;81; 3;
3
3
в виде степени числа 3.
23. Системы показательных уравнений и неравенств
24.
1. Решить уравнение:1)5 0,2; 2)25 5;
х
х
3х
1
3) 1.
3
25.
2. Решить неравенство:1
1)
3
х
7
1
;
27
2) .
10
2х
26.
3. С помощью графиков функциих
1
у и у
решить
2
2
х
неравенство:
х
1 х
1) ;
2 2
х
х
1
2 ) .
2
2
27. ЛОГАРИФМЫ
28.
1.Решить уравнение:1)2 8
х
х
1
1
2) 2 ; 3) 16;
4
2
х
х
1
4)2 1; 5) 0;
2
х
6)2 2.
х
29.
2. С помощью графикафункции у 2 х найти
приближенные значения
корней уравнения:
2 2
1) , 2)2 х 3; 3)2 х 6.
х 3
После введения понятия
логарифма стоит вернуться к
рис. 23 и отметить абсциссы
точек пересечения графика
функции у 2 х с прямыми
2
у , у 3, у 6. Это
3
2
х log 2 , х log 2 3,
3
х log 2 6,
30. Логарифмическая функция, ее свойства и график
31.
1. Выяснить, при каких значения химеет смысл выражения:
х
1)0,3 ; 2) log 0,3 х; 3) log 0,3 х ;
4) log х 1,5;
2
5) log х 15.
32.
2.Найти у, если:1) ln у 1; 2) lg у 0;
1
3) ln у ;
2
4) lg у 2.
33.
3.Записать каждое из чисел0; 1; -1; 2; 1
1
;
2
2
в виде логарифма по основанию
5.
34.
4. Решить уравнение:1
1)10 100; 2)е ;
е
х
3)2 3;
х
х
4)10 7.
х
35.
5. Решить неравенство:3
1)6 6 ;
х
2)0,1 0,1 ;
х
2
3)10 15; 4)е е
lg х
ln х
5)10 10 ;
lg х
lg 2
1
6)
2
ln 0,3
log 1 х
2
2.
;
36. Логарифмические уравнения
37.
1.Решить уравнение2
х
32
2
х
0,5
2
х
7
2
х
2
2
log2 9
x 1
38. 2.Вычислить
1) log 2 48 log 2 31
2) log 6 4 log
6 24
3) log 5
4
125
39.
3.Решить уравнение1) log
2
3
X 2
2) log x 9 2
3) log x 1 0
4) log 8 log 3 x 0
5) log 5 ( 2 x 1) log 5 7
6) log 3 x log 3 4
2
7) 2 log 3 x log 3 4
40. и
4.Выяснить какое уравнение являетсяследствием другого:
1) log 5 x log 5 ( x 4) 1
log 5 ( x( x 4)) 1
и
2) log 3 x log 3 4 2 log 3 x log 3 4
2
41. Логарифмические неравенства
42.
1.Записать каждое из чисел:1
1)1;0;-1;
в виде логарифма по
3
основанию 2.
1
2)-3;-1;0; 2 ;1 в виде логарифма по
1
основанию
3
43.
2)Найти область определения функции:1) y lg( x 1)
2) y log 5 (3 x)
3) y ln x
2
4) y log 1 ( x 1)
2
3
44.
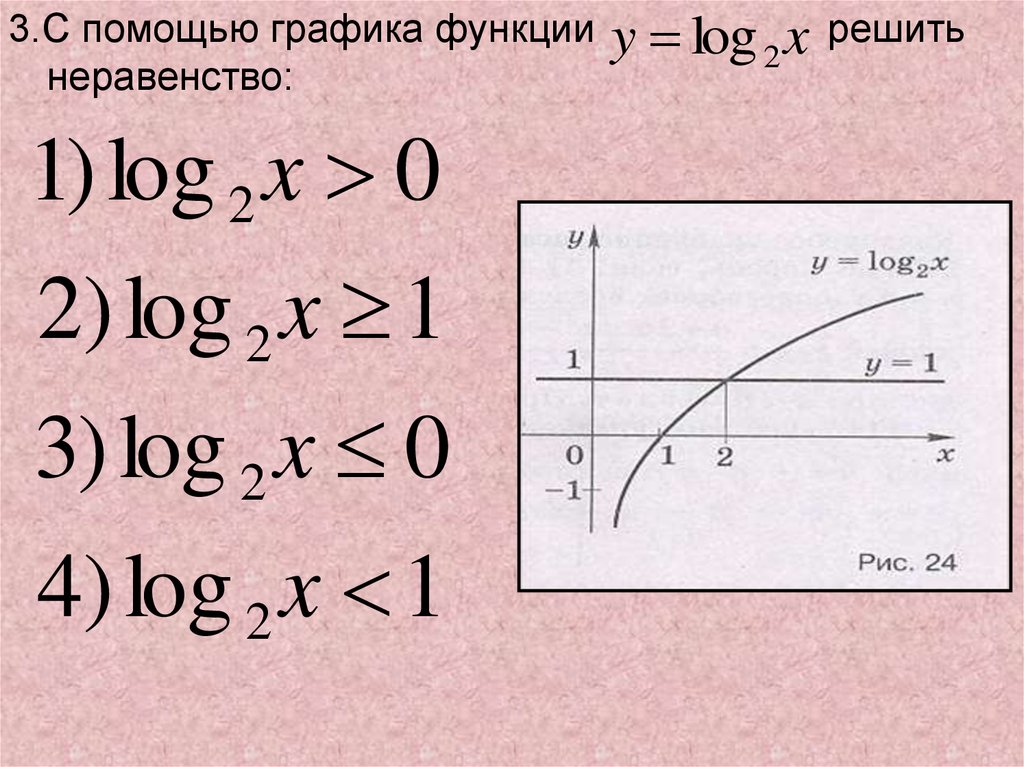
3.С помощью графика функциинеравенство:
1) log 2 x 0
2) log 2 x 1
3) log 2 x 0
4) log 2 x 1
y log 2 x
решить
45.
4.Выяснить возрастающей илиубывающей является функция:
1) y log x
2) y lg x
3) y log 1 x
e
46.
5.Среди соотношений х<3,x>3,0<x<3выбрать решение неравенства:
1) log 5 x log 5 3
2) log 5 x log 5 3
3) log 1 x log 1 3
5
3
4) log 1 x log 1 3
5
5
47. Определение синуса, косинуса, тангенса
48.
1.Назвать хотя бы один угол, накоторый нужно повернуть точку
Р(1;0) вокруг начала координат,
чтобы получить точку:
1 3
)
А(-1;0),В(1;0),С(0;-1),D(0;1),Е ( ;
2 2
49.
2.Определть четверть, вкоторой находиться точка,
полученная поворотом точки
Р(1;0) на угол равный 2;3,7;5;2;-3,7;-5 (радиан)
50.
3.Сравнить числа:2
и 1
2
3
2
и 4
и 4
51.
4.Верно ли высказывание:«Координаты точки,
полученные поворотом точки
Р(1;0) на угол 6 рад, имеют
разные знаки?»
52. Зависимость между синусом, косинусом и тангенсом одного и того же угла
53.
1.Найди абсциссы точек,принадлежащих окружности с
центром в начале координат и
радиусом 1,если эти точки
имеют ординату 0,8.
54.
2.Дана окружность с центром вначале координат и радиусом
R=1.Принадлежат ли ей точки:
3 4
1
3
2 2
À( ; ), Â(0,3;0,7), Ñ ( ; ), D(
;
)?
5 5
2
2
2 2
55.
3.Определить знаки значений:5
7
1
sin 190, cos 275, tg
, sin
, cos , tg 6
6
6
3
56.
4.Сравнить значениявыражений:sin 3,8 и sin
0,25; cos 2,1 и cos 0,75.
57. Синус, косинус, тангенс
58.
1.Закончить запись формулыдвойного числа:
1) cos 4 cos 2 __________
2
2) sin 5 2 sin _____________
59.
2.Выразить cos 3 через cos 62
60.
51
3.Вычислить 1 соs5 , если sin
2
3
61.
4.Найти значение выражения:1)3 cos 3 , если cos 1,5 sin 1,5 0,7;
2
2)
1 cos
2 sin
2
2
, если tg
2
2
3.
62.
5.Решить уравнение:1) cos 3x sin 3x 1
2
2
2)2 sin 2,5 x * cos 2,5 x o
63. Формулы приведения
64.
1.Назвать углы, синусыкоторых равны синусу угла
30 градусов.
65.
2.Назвать углы, косинусыкоторых равны косинусу углу
120 градусов
66.
3.На какой угол повернули точкуР(1;0),чтобы получить точку М?
Сравнить значения синуса и косинуса
чисел, соответствующих точкам А и М.
67.
4.Сравнить синусы икосинусы углов è
68. Тригонометрические уравнения
69.
1.Имеет ли смыслвыражение:
3
4
arccos ; arccos( 0,7); arccos ?
4
3
70.
1.Может ли arccos a принимать12
13
значение, равное ; ; ?
7
13
12
71. Уравнения sin x=a
72.
1.Составить уравнение для решенияследующей задачи: «Найти все углы, на
которые нужно повернуть точку
Р(1;0),чтобы получить точки А и В,
имеющие одинаковые абсциссы, равные
0,7.»
73.
2.Доказать,что:2
1) arccos
;
2
4
2
3
2) arccos(
)
.
2
4
74.
3.Объяснить,почему не существует числа а,такого, что
7
6
à
6
, arccos
5
a.
75.
4.Ордината точки М единичной окружности равна1/2.1)Найти координаты точки N,симметричной М
относительно оси ординат.2)Назвать меры, какихлибо трёх углов поворота точки Р(1;0) вокруг
начала координат, в результате которых
получается точка М; точка N.3)Записать все углы,
на которые нужно повернуть точку Р(1;0),чтобы
получить точку М, точку N.
76.
5.Ордината точки М единичной окружности равна –1/2 .1)Найти координаты точки N.2)Назвать меры
каких-либо трёх углов, на которые нужно
повернуть точку Р(1;0) вокруг начала координат,
чтобы получить точку М, точку N.3)Записать все
углы,на котрые нужно повернуть точку Р(1;0)
вокруг начала координат, чтобы получить точку М,
точку N.











































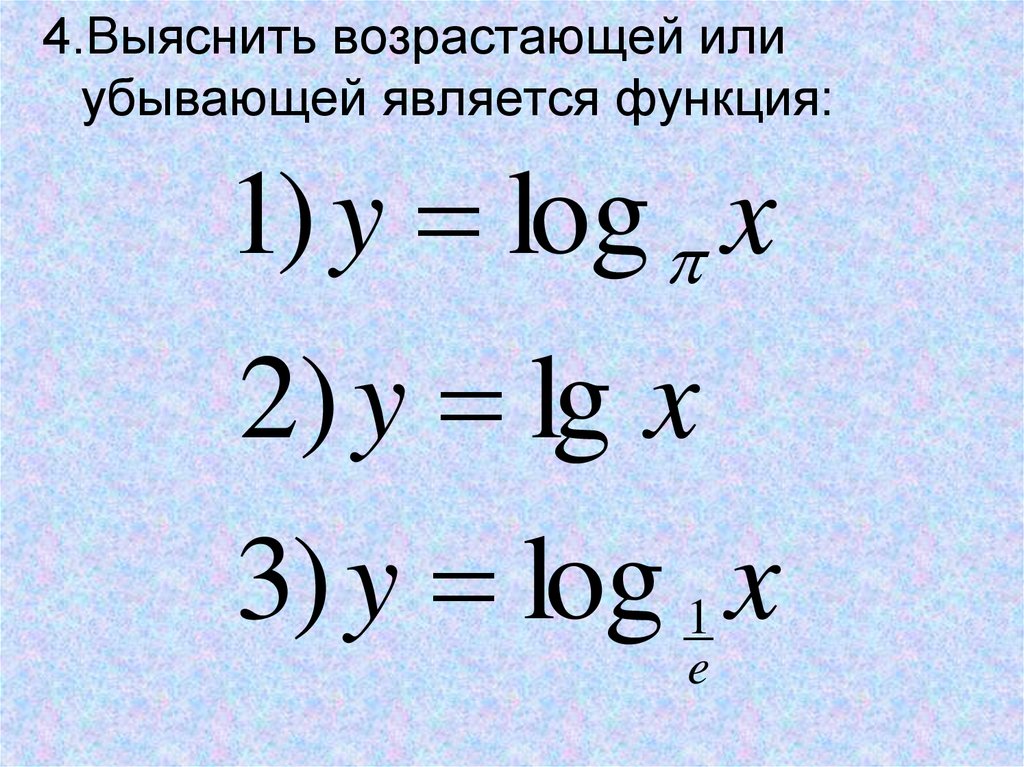































 Математика
Математика








