Похожие презентации:
Тригонометрия. Учебное пособие для техникума
1. Тригонометрия
Учебное пособие для техникума2. Тригонометрия
Учебный элемент № 1Учебный элемент № 2
Учебный элемент № 3
Учебный элемент № 4
Учебный элемент № 5
Учебный элемент № 6
Учебный элемент № 7
Учебный элемент № 8
Учебный элемент № 9
Учебный элемент № 10
Учебный элемент № 11
Учебный элемент № 12
3. Понятие радиана и градуса. Формулы перевода градусной меры угла в радианную меру и обратно.
–Цели
Усвоить понятие радиана
Познакомится с формулами перевода
градусной меры угла в радианную
меру и обратно
Вычислять значение градусной меры
угла и радианной меры угла
НА ОГЛАВЛЕНИЕ
–
Содержание обучения:
Понятие радиана.
Связь радианной и градусной мер
углов.
Распределение точек на единичной
окружности.
ДАЛЬШЕ
4. § 1. Радианное измерение угловых величин.
При радианном измерении дуг (и соответствующих им центральных углов) за единицуизмерения принимается радиан– дуга, длина которой равна радиусу этой дуги.
Радианная мера дуги вычисляется по формуле:
a=l/R,
(1)
где а– радианная мера дуги, l – длина дуги окружности, R – радиус этой дуги.
Формула перехода от градусного измерения к радианному имеет вид:
a=(π/1800 )β
(2),
где β – градусная мера дуги (угла).
0
Радианная мера 1 равна 0,0175 радиана.
Формула перехода от радианного измерения к градусному имеет вид
β=(1800 /π)a
(3)
градусная мера 1 радиана равна 57 017’44’’,8 ≈570 ,3.
Длина дуги окружности равна радианной мере дуги, умноженной на радиус этой дуги:
l=aR
(4)
Площадь кругового сектора равна половине радианной меры дуги сектора,
умноженной на квадрат радиуса круга: Sсект=aR2 /2
(5)
Полный круг составляет 360 градусов, т.е.2п (2*1800).
Если рассматриваемый угол больше 2п, то обозначение 2пn, где n – градусы.
Положительным направлением отсчета углов считается поворот по единичной
окружности (т.е. окружности с радиусом равным 1) против часовой стрелки, а
отрицательным – по часовой стрелке.
НА ОГЛАВЛЕНИЕ
ДАЛЬШЕ
5. ТРЕНИНГ
1. Выразить в радианной мере величинуугла в 900.
По формуле (2) a = ( π / 1 8 0 0 ) β ,
. 2. Выразить в градусной мере величину
угла в
7п /6 рад.
По формуле (3) β = ( 1 8 0 0 / π ) a
900 = (п/1800 ) 900=п / 2 (рад)
7п / 6 =(1800 /п)( 7п / 6 ) = 2100
0 = 00
п / 6 = 300
п / 4 = 450
п / 3 = 600
п / 2 = 900
2п / 3 = 1200.
. 3. Построить на единичной окружности
точки:
0, п/ 6, п / 4, п / 3, п / 2, 2п / 3.
Построить единичную окружность;
Зная, что п = 1800, посчитать чему
равны углы в градусах;
Поставить значения углов на
окружности.
НА ОГЛАВЛЕНИЕ
ДАЛЬШЕ
6. ТЕСТ
заданияответы
1. переведите градусную меру угла в
радианную: 3000, - 1350, 2100.
5п / 3; - 3п / 4; 7п / 6.
2. переведите радианную меру угла в
градусную: 5п / 4; 3,5п; - 5п / 9.
2250; 6300; - 1000.
3. назовите координатную четверть,
которой принадлежит угол a , равный
10000, 20000.
4. Вычислите радиус окружности, если ее
дуга длиной 0,84 м содержит 1,5 радиана.
IV четверть, III четверть.
0,56
5. Поставьте точки на окружности.
-2000; 5000; 5п / 9; - п / 2.
Посттест на «3»
НА ОГЛАВЛЕНИЕ
Посттест на «4» и «5»
7. ПОСТТЕСТ на «3»
–1-й вопрос
выразите в радианной мере величину угла в 220.
а) 90 ; б) 11 ; в) 4 .
90
30
11
НА ОГЛАВЛЕНИЕ
Посттест на «4» и «5»
8. 2- й вопрос
выразите в градусной мере величину угла ва)250;
б)
220;
НА ОГЛАВЛЕНИЕ
в)
150.
12
.
9. 2 вопрос
выразите в градусной мере величину угла ва)250;
б)
220;
НА ОГЛАВЛЕНИЕ
в)
150.
12
.
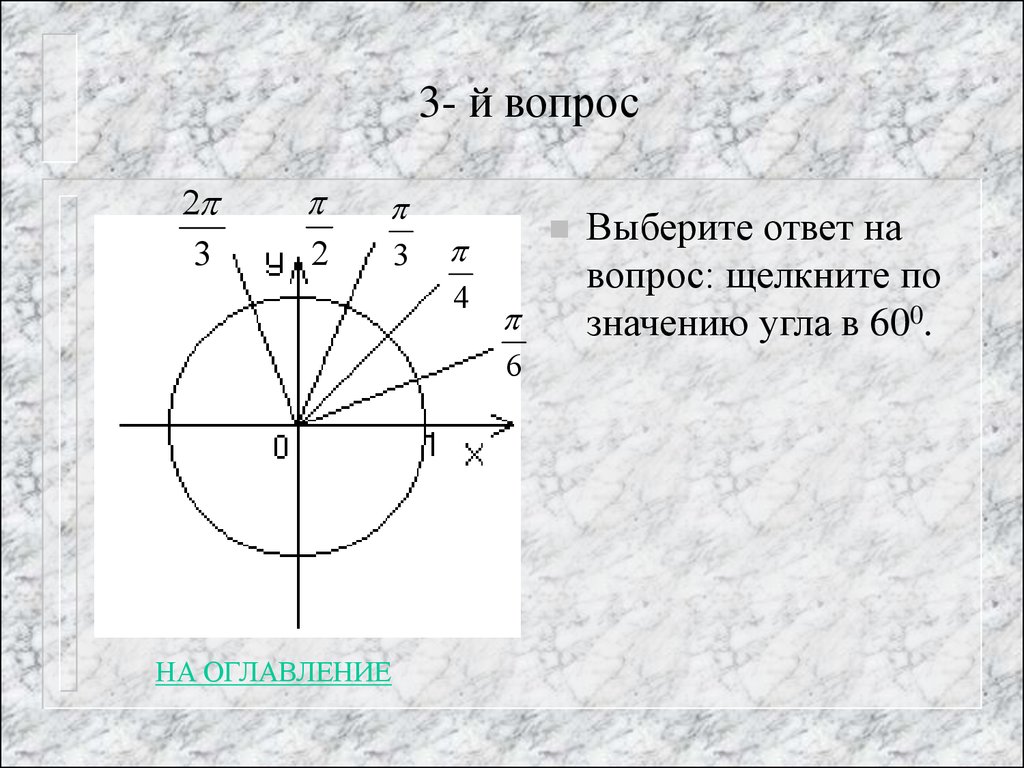
10. 3- й вопрос
23
2
3
НА ОГЛАВЛЕНИЕ
4
6
Выберите ответ на
вопрос: щелкните по
значению угла в 600.
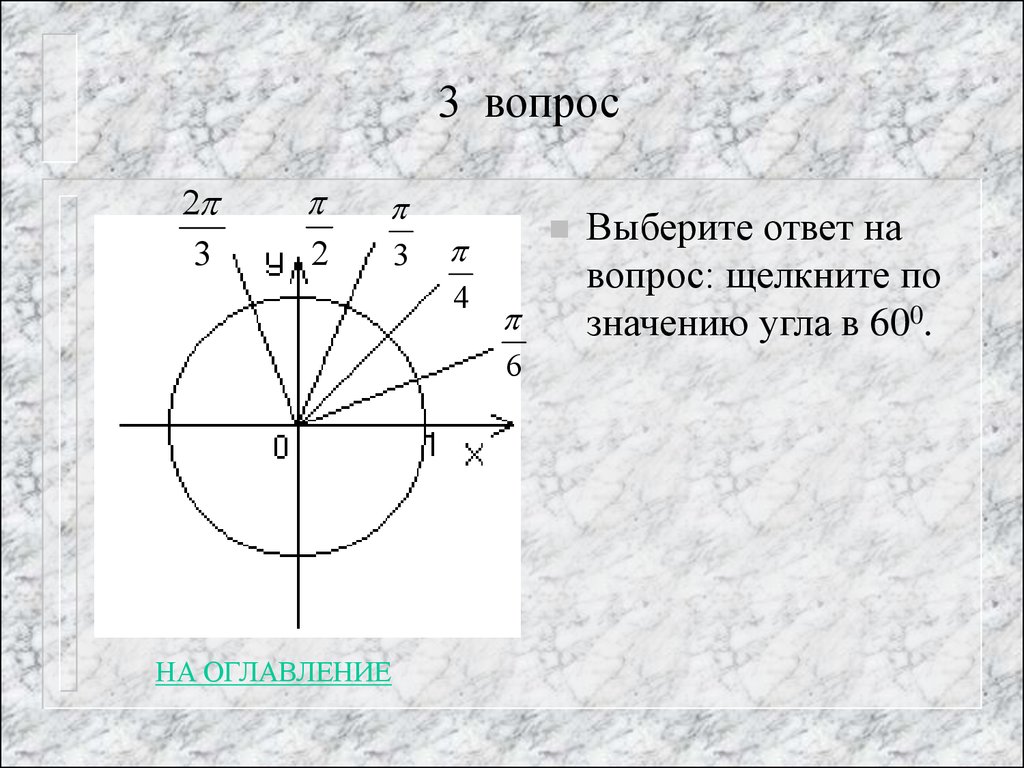
11. 3 вопрос
23
2
3
НА ОГЛАВЛЕНИЕ
4
6
Выберите ответ на
вопрос: щелкните по
значению угла в 600.
12.
На оглавление13.
На оглавление14. НА «4» и «5»
Выразите в радианной мере величины углов: а) 400;б) 1200; в) 200; г) 1350
Выразите в градусной мере величины углов: а) ;
2
б) 2 ; в) .
3
Угловая величина дуги АВ равна 2п/3, а ее радиус
равен 3 м. Найдите длину дуги АВ.
Найдите координаты точки единичной окружности,
полученной поворотом точки (1;0) на угол:
а)
; б) ; в) 3 ; г) 2 .
2
2
Найдите все углы, на которую нужно повернуть точку
(1;0), чтобы получить точку с координатами (-1;0).
НА ОГЛАВЛЕНИЕ
15. Тригонометрические функции числового аргумента. Основные тригонометрические тождества.
–Цели
Познакомиться с определением
тригонометрических функций;
Находить значения
тригонометрических функций
числового аргумента;
Применять основные
тригонометрические тождества для
нахождения тригонометрических
функций.
На оглавление
–
Содержание обучения:
Тригонометрические функции
числового аргумента;
Основные тригонометрические
тождества.
Дальше
16. § 1. Тригонометрические функции числового аргумента
Абсцисса Х точки Мα числовой единичной окружности (см.рис.) называетсякосинусом числа α: Х = cos α
(1)
Ордината Y точки Мα числовой единичной окружности называется синусом
числа α:
Y = sin α
(2)
Областью определения косинуса и синуса служит множество всех
действительных чисел, т.е. D(cos α)=R, D(sin α)=R.
Отношение синуса числа α к его косинусу называется тангенсом числа α:
sin a
tga
(3)
cos a
Область определения тангенса – множество всех действительных чисел за
исключением чисел вида.
Отношения косинуса числа α к его синусу называется котангенсом числа α:
соsa
сtga
(4)
sin a
Область определения котангенса – множество всех действительных чисел за
исключением чисел вида.
Функции cosa и sina ограничены, т.к. Е(cosa) = [–1;1], E(sina) = [-1;1].
Функции tga и ctga неограничены, т.к. каждая из них может принимать
любое действительное значение , т.е. E(tga) = R, E(ctga) = R.
На оглавление
Дальше
17. § 2. Основные тригонометрические тождества
sin a cos a 1;2
2
tga ctga 1, a
k
2
.k ;
1
1 tg a
, a k , k ;
2
cos a
2
1
2
1 ctg a
, a k , k .
2
sin a
2
На оглавление
Дальше
18. Тренинг
Найти область определенияфункций:
1) у=sin3x
2) y=1/sinx
3) y=tg4x
На оглавление
1) Здесь х – любое
действительное число, т.к. график
синуса расположен вдоль оси
абсцисс;
2) sinx не равен 0 (т.к. он в
знаменателе), значит x не равно
пk, k€Z;
3) т.к. область определения
тангенса (-п/2; п/2), то 4x не
должно быть равно п/2+пk,
значит x не должно быть равно
п/8 + пk/4, k€Z;
Дальше
19. Дано: sinx=3/5, x принадлежит (п/2; п). Вычислить: 1) cosx; 2) tg x; 3) ctgx.
1)Выразим косинус из первоготригонометрического тождества:
(во второй четверти косинус
имеет знак “–“).
Подставляем известное значение
синуса и вычисляем косинус.
2) Используем определение
тангенса (см.1 параграф);
подставим значение синуса и
найденное значение косинуса.
1) cos x 1 sin 2 x
cos x 1 (3 / 5) 2 = – 4/5.
2) tg x = (3/5) : (–4/5) = – 3/4
3) ctg x = – 4/3.
3) аналогично 2) найдем
котангенс.
На оглавление
Дальше
20. Доказать тождество:
sin x1 cos x
2
1 cos x
sin x
sin x
1 cos x
2 sin 2 x 1 2 cos x cos 2 x
2
sin x
sin x
sin x
(1 cos x) sin x
sin x
1 cos x
1 1 2 cos x
2 2(1 cos x)
2
(1 cos x) sin x sin x (1 cos x) sin x sin x
2
2
;
sin x sin x
На оглавление
Дальше
21. Тест
Упростите выражения:1. sin a tg a cos a;
2
2
2
2. sin 4 a cos 4 a cos 2 a;
cos 3 a sin 3 a
3.
;
1 sin a cos a
4. sin a cos a(tga ctga).
Ответы:
1.
1
2
cos a
2. sin2 a.
3. cos a – sin a.
4. 1
Посттест на «3»
На оглавление
Посттест на «4» и «5»
22. ПОСТТЕСТ НА «3»
1 вопросПри каких значениях аргумента принимает
наименьшее и наибольшее значения
следующая функция:
Y = 0,5 cos2x
Ответы:
А) Унаиб.= 0,5; Унаим. = -0,5.
Б) Унаиб.= 2; Унаим. = -2.
В) Унаиб.= 5; Унаим. = -5.
На оглавление
23. 2 вопрос
Найдите область определения функцииY = sinx + cosx ;
Ответы:
А) х € [- 1; 1];
Б) х € [- 0,5; 0,5];
В) х – любое действительное число.
На оглавление
24. 2 - й вопрос
Найдите область определения функцииY = sinx + cosx ;
Ответы:
А) х € [- 1; 1];
Б) х € [- 0,5; 0,5];
В) х – любое действительное число.
На оглавление
25. 3 вопрос
Дано: tgx = – ¾, II четверть. Вычислитьsinx, cosx, ctgx.
Ответы:
А) sinx =-3/5; сosx = -4/5; ctgx = 4/3.
Б) sinx =3/5; сosx = -4/5; ctgx = -4/3.
В) sinx =4/3; сosx = -3/5; ctgx = -4/5.
На оглавление
26. 3 – й вопрос
Дано: tgx = – ¾, II четверть. Вычислитьsinx, cosx, ctgx.
Ответы:
А) sinx =-3/5; сosx = -4/5; ctgx = 4/3.
Б) sinx =3/5; сosx = -4/5; ctgx = -4/3.
В) sinx =4/3; сosx = -3/5; ctgx = -4/5.
На оглавление
27. НА «4» и «5»
1. Дано: tgx = – ¾, II четверть. Вычислитьостальные тригонометрические функции.
2. Докажите тождества:
cos x(1 tgx)(1 tgx) cos x sin x;
tgx
sin 4 x
tgx ctgx
2
3.
4
4
1 (sin x cos x) 2
2tg 2 x;
sin x cos x ctgx
Упростите выражения:
(sin x cos x) 2 (sin x cos x) 2 ;
sin 2 x cos 4 x sin 4 x
На оглавление
28. Основные свойства тригонометрических функций.
Цели1. Находить знаки значений
тригонометрических функций;
Содержание обучения:
1. Знаки значений тригонометрических
функций.
2. Четные и нечетные функции.
2. Какие функции являются четными,
нечетными и периодическими;
3.
Находить период функции.
3. Периодичность тригонометрических
функций.
4. Свойства и графики
тригонометрических функций.
На оглавление
Дальше
29. § 1. Знаки значений тригонометрических функций. Знаки тригонометрических функций по четвертям приведены в таблице:
§ 1. Знаки значений тригонометрических функций.Знаки тригонометрических функций по четвертям приведены в таблице:
II
III
IV
0<a<п/2
п/2<a<п
п<a<3п/2
3п/2<a<2п
Функция
sina
+
+
–
–
cosa
+
–
–
+
tga
+
–
+
–
ctga
+
–
+
–
Четверть
I
На оглавление
Дальше
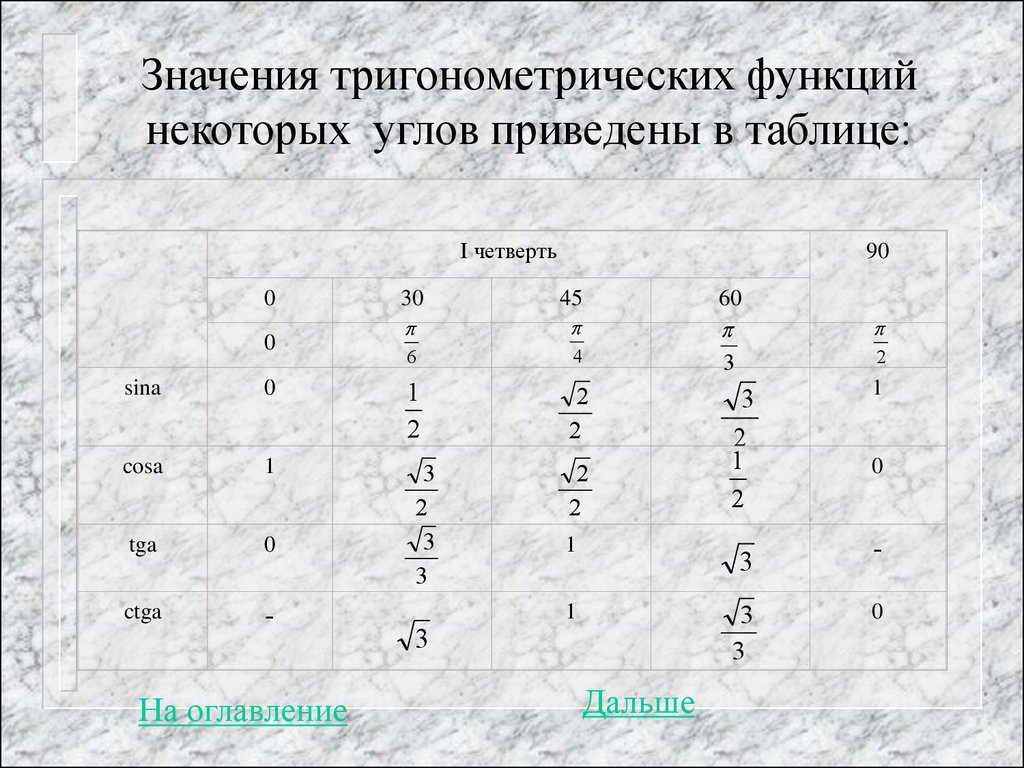
30. Значения тригонометрических функций некоторых углов приведены в таблице:
I четверть90
0
30
45
60
0
6
4
3
1
2
2
2
sina
0
cosa
1
tga
0
ctga
-
На оглавление
3
2
3
3
3
2
3
2
1
2
1
1
3
-
1
3
3
0
2
2
Дальше
0
31. § 2. Четные и нечетные функции.
Опр.1: функция f называется четной, если с каждым значением переменной х из областиопределения f значение ( - х) также входит в область определения этой функции и при
этом выполняется равенство: f (- x) = f (x).
Опр.2: функция f называется нечетной, если с каждым значением переменной х из
области определения f значение ( - х) также входит в область определения этой функции
и при этом выполняется равенство: f (- x) = --f (x).
График любой четной функции симметричен относительно оси ординат, а гарфик любой
нечетной функции симметричен относительно начала координат.
Теорема: косинус – четная функция, а синус, тангенс и котангенс – нечетные функции.
Свойства четности и нечетности тригонометрических функций выражаются
следующими формулами: sin(–a) = – sina;
cos(–a) = cosa;
tg(–a) = – tga;
ctg(–a) = – ctga.
На оглавление
Дальше
32. § 3. Периодичность тригонометрических функций.
Опр.: функция f называется периодической, если существует такое число , что прилюбом из области определения f числа ( – ) и ( + ) также принадлежат этой
области и при этом выполняется равенство f ( - ) = f ( ) = f ( + ).
В этом случае число называется периодом функции f. Ее периодами являются также
числа вида n , n , n 0.
Теорема: функции синус, косинус, тангенс и котангенс являются периодическими.
Наименьший положительный период синуса и косинуса равен 2 .
Наименьший положительный период тангенса и котангенса равен ..
Свойства периодичности тригонометрических функций можно выразить тождествами:
sin = sin ( +2 k), k ;
cos = cos ( +2 k), k ;
tg = tg ( + k), k ;
На оглавление
ctg = ctg ( + k), k ;
Дальше
33. § 4. Свойства и графики тригонометрических функций.
1.Синус
F(x) = sin x.
Свойства:
1) Область определения: R;
2) Область значений: [– 1; 1];
3) Четность (нечетность): Нечетная;
4) Наименьший положительный период: 2 ;
5) Координаты точек пересечения графика f с осью Ох: ( n; 0);
6) Координаты точек пересечения графика f с осью Оy: (0; 0);
7) Промежутки, на которых f принимает положительные значения: (2 n; + 2 n);
8) Промежутки, на которых f принимает отрицательные значения: (– + 2 n; 2 n);
2 2 n; 2 2 n
;
3
10) Промежутки убывания:
;
2 2 n; 2 2 n
11)Точки минимума: 1; 2 2 n; ; 12) Точки максимума:
9) Промежутки возрастания:
На оглавление
.
1; 2 n
2
Дальше
34.
1.Косинус
F(x) = cos x.
Свойства:
1) Область определения: R;
2) Область значений: [– 1; 1];
3) Четность (нечетность): Четная;
4) Наименьший положительный период: 2 ;
5) Координаты точек пересечения графика f с осью Ох: (
2
+ n; 0);
6) Координаты точек пересечения графика f с осью Оy: (0; 1);
7) Промежутки, на которых f принимает положительные значения: (
2
+2 n; 2 + 2 n);
8) Промежутки, на которых f принимает отрицательные значения: ( 2 + 2 n; 3 +2 n);
9) Промежутки возрастания:
10) Промежутки убывания:
11)Точки минимума:
2 n;2 n
2 n; 2 n
1; 2 n; ;
На оглавление
2
;
;
12) Точки максимума: 1;2 n
Дальше
.
35. Тренинг. Решение упражнений.
Алгоритм решенияРешение
Какие знаки имеют следующие выражения:
1) cos 150;
1)
90<150<180 (II четверть), cos 150<0;
2) sin 320;
2)
270<320<360 (IV четверть), sin320<0;
3) tg 220;
3)
180<220<270 (III четверть), tg220>0;
4) ctg 400.
4)
360<400<360+90 (I четверть), ctg
400>0.
Используя формулы параграфа
Упростить:
1) sin 2 ( a) cos( a) tg ( a);
3
2) sin( ) cos( ) tg ( 2 ).
2
Вычислить:
tg 2 ( / 3) ctg ( / 6) 2 sin( / 3)
sin 4 cos(3 / 2) 2 cos( / 3).
На оглавление
1) sin 2 ( a ) cos( a ) tg ( a ) ( sin a ) 2 cos a tga
sin 2 a cos a tga.
3
3
) cos( ) tg ( 2 ) sin
cos tg 2
2
2
1 ( 1) 0 0.
2) sin(
По таблице значений находим значение аргумента
каждой тригонометрической функции:
( 3) 2 3 2
3
1
0 4 0 2 2
2
2
Дальше
36. ТЕСТ
Какие знаки имеют следующие выражения:1. 1. sin 170
2. cos 300
3. tg 160
4. ctg 315
5. tg 450
6. sin 400
7. sin (7п/3)
8. cos (4п/3)
9. 9. sin (5п/4)
10. cos (7п/5)
11. tg (8п/3)
12. ctg(9g/4)
Ответы:
2. +
3. –
4. –
5. Не сущ. 6. +
7. +
8. –
9. –
11. –
12. +.
1.
+
10. –
Упростите:
1) cos( ) sin( / 2) sin( 3 / 2);
2)2 cos( ) cos( 2 ) sin( 3 / 2).
1. 1
–2
Посттест на «3», «4» и «5»
На оглавление
37. Формулы сложения
ЦелиСодержание обучения:
Повторить определения
тригонометрических функций;
1.
Косинус и синус суммы и
разности.
Познакомится с формулами
сложения тригонометрических функций;
2.
Тангенс суммы
Научиться применять формулы
сложения
На оглавление
Дальше
38. § 1. Косинус и синус суммы и разности.
Формула косинуса суммы:cos(a + в) = cosa cosв – sin а sin в.
(1)
Так как cos (– в) = cos в и sin(–в) = – sin в, из этой формулы следует:
cos(a – в) = cosa cosв + sin а sin в.
(2)
Формула синуса суммы имеет вид:
sin(а + в) = sin а cosв + cosa sin в.
(3)
заменив в формуле (3) в на (–в), приходим к формуле синуса разности:
sin(а – в) = sin а cosв – cosa sin в.
(4)
На оглавление
Дальше
39. § 2. Тангенс суммы.
Вывод формулы тангенса суммы дается с помощью предыдущих формулкосинуса и синуса суммы и определения тангенса.
Формула тангенса суммы:
Tg (а + в) = tg а +tg в
1 – tg a tg в , а = п/2(2к+1), в= п/2(2к + 1), tga tgв = 1
(5)
подставляя в формулу (5) вместо в (–в) получим
формулу тангенса разности:
Tg (а – в) = tg а –tg в
1 + tg a tg в, а = п/2(2к+1), в= п/2(2к + 1), tga tgв = 1
На оглавление
Дальше
(6).
40. Тренинг. Решение упражнений
Вычислить:3
5
1. sin( ), если sin , cos ,
5
13
3
( ; ), ( ; ).
2
2
ответы
3
4
5
12
cos 1 ( ) 2 , sin 1 ( ) 2
5
5
13
13
sin( )
3
5
4
12
33
( ) ( ) ( ) .
5
13
5
13
65
вычислим sin 750 и cos 750.
Заметим, что 750 = 450 + 300
Поскольку синусы и косинусы
углов 45 и 30 градусов известны,
с помощью формул синуса и
косинуса суммы находим, чему
равны синус 750 и косинус 750.
На оглавление
Sin750 =sin(300+45)=sin30 cos45 +
cos30 sin45 = 1 2 3 2 2 6
2
2
2
2
4
Cos75=cos(30 +45 )=cos30 cos45 –
sin30 sin45 = 3 2 1 2 6 2
2
2
Дальше
2
2
4
41.
Вычислим выражения:1) sin 20 0 cos 40 0 cos 20 0 sin 40 0 sin( 20 0 40 0 )
1) sin 20 0 cos 40 0 cos 20 0 sin 40 0
sin 60 0 3 / 2.
2) cos 47 0 cos 17 0 sin 47 0 sin 17 0.
2) cos 47 0 cos 17 0 sin 47 0 sin 17 0 cos( 47 0 17 0 )
cos 30 0 3 / 2.
Доказать тождества:
2 cos 2 cos( )
4
1)
tg ;
2 sin( ) 2 sin
4
Упрощая левую часть равенства, получим
2
cos cos( )) cos cos cos cos
2
4
4
4
2
2(sin( )
sin ) sin cos cos sin
4
4
4
2
2(
sin
cos
4
4
sin
sin
sin
sin
4
4
sin
tg .
cos
тождество доказано.
На оглавление
Дальше
42. ТЕСТ
задания1. вычислите: а)sin1050; б)cos150.
ответы
а)sin(45+60)=sin45cos60+cos45sin60=
б)cos(60-45)= 6 2
4
2. вычислите:
а) cos250 sin650 +sin250 cos650;
б) cos 7п/10 cosп/5 + sin 7п/10 sinп/5
а) sin(65+25)= sin90 = 1;
б) cos (п/2) =0
3. Докажите тождество:
а) cos(a+в)cos(a – в)+ sin(а + в) sin(а – в)=cos2в
б) tga + tg(450 – a) = 1
1 – tgatg(450 –a)
Посттест на «3»
На оглавление
Посттест на «4» и «5»
6 2
4
43. ПОСТТЕСТ НА «3»
1 вопрос1. вычислите:
sin п/6 cos п/3 + cos п/6 sin п/3
Ответы:
А) 1
Б) 0,5
В)-1
44.
2 вопрос2. вычислите cos(a + в), если известно, что
sin а =sin в = 5/13 и 0<а<п/2, п/2<в<п
Ответы:
А) 1
Б) –1
В) 0
45.
2-й вопрос2. вычислите cos(a + в), если известно, что
sin а =sin в = 5/13 и 0<а<п/2, п/2<в<п
Ответы:
А) 1
Б) –1
В) 0
46. ПОСТТЕСТ НА «4» И «5»
1. вычислите:cos п/7 sin8п/7 – sin п/7 cos8п/7
2. вычислите cos(п/3 – a), если известно,
что cos а = 2/5 и 3п/2<а<2п.
3. докажите тождество:
cos(а + в) cos (a – в)= сos2 в – sin 2a
4.упростите выражение:
cos(а + п/3) – cos(а – п/3)
На оглавление
47. Формулы двойного и половинного аргументов
Цели:Повторить определения тригонометрических
функций;
Содержание обучения:
1.
Тригонометрические функции
двойного аргумента.
Повторить формулы сложения
тригонометрических функций;
2. Тригонометрические функции
половинного аргумента
Познакомится с формулами двойного и половинного
аргументов тригонометрических функций;
Научиться применять формулы двойного и
половинного аргументов
На оглавление
Дальше
48. § 1. Тригонометрические функции двойного аргумента
Формулы сложения позволяют выразить sin 2a, cos 2a и tg 2a через тригонометрические функцииугла а. Положим в формулах:
cos(a + в) = cosa cosв – sin а sin в; sin(а + в) = sin а cosв + cosa sin в;
Tg (а + в) = tg а + tg в
1 – tg a tg в
в равным а. Получим тождества:
sin 2a = 2 sin a cos a,
(1)
cos 2a = cos2 a – sin2 a,
(2)
tg 2a = 2 tg a , а= п/2+пk, а=п/4+пk/2.
(3)
1 – tg2 a
ctg2a = ctg2 a –1 , а= пk/2
(4)
2 ctga
Эти тождества называют формулами двойного угла.
Если выразить правую часть формулы (2) через синус или косинус, то приходим к следующим
тождествам:
cos 2a = 2 cos2 a – 1
(5)
2
cos 2a = 1 – 2 sin a
(6)
На оглавление
Дальше
49. § 2. Тригонометрические функции половинного аргумента
sin2 a = 1 – сos 2aЕсли из формул (5) и (6) выразить cos2 a и sin2 a, получим:
cos2 a = 1 + cos 2a
2
заменим теперь а на а/2, получим:
sin2 a = 1 – сos 2a
cos2 a = 1 + cos 2a
2
2
2
2
значит :
sin a = + 1 – сos a
(7)
cos a = + 1 + cos a
(8)
2
2
2
tg a = sin a/2 = sin a
(9)
2
tg a = + 1 – cos a
,
а=п(2k+1) (10)
2
cos a/2
1+cos a.
ctg a = cos a/2 = sin a
2
(11)
1 + cos a
ctg a = + 1 + cos a , а=2п
(12)
2
sin a/2
1–cos a.
2
1 – cos a
В формулах (7) и (8), знак перед корнем определяется по знаку четверти, которой
На
оглавление
Дальше
принадлежит дуга а/2.
В формулах (10) и (12), знак перед корнем берется так, чтобы он совпадал со знаком
tg(a/2), т.е. +, если I
50. Тренинг. Решение упражнений
известно, что sin a = 0,6, и 0<a<п/2. Вычислите sin2a, cos2a, tg2a.Из основного тригонометрического тождества: cos2 a+ sin2 a = 1 выразим cosa и
вычислим его значение: cosa = 0,8
найдем sin 2a = 2 sin a cos a: sin 2a = 2*0,6*0,8 =0,96
Найдем cos 2a = cos2 a – sin2 a: cos 2a = 0,64 – 0,36 = 0,28
Найдем tg 2a = sin 2a :
tg 2a = 0,96/0,28 = 24/7
сos 2a
1.
упростите: 1 + cos a tg2 a – cos2 a
1 – cos a
2
разложим тангенс половинного угла: tg2 a = 1 – cos a
2 1 + cos a
Сократим, приведем подобные: 1 + cos a 1 – cos a – cos2a=1–cos2a = sin2 a
1 – cos a* 1 + cos a
2.
3.
Вычислить tg(a/2), если: sina = 4/5 и п/2<a<п;
4
3
Находим cos 1 ( ) 2
5
5
На оглавление
По формуле (9)
tg
2
4
3
(1 ) 2.
5
5
Дальше
51. ТЕСТ
Задания1. известно, что cos a = –5/13 и sin a >0.
Найдите sin2a, cos2a, tg2a.
Ответы
sin2a= 120 ; соs2а=
tg2a=
2. найдите sina/2, cosa/2 и tga/2, если
cosa= – 12/13 и а принадлежит
IIIчетверти.
sin
169
120
119
119
169
;
а
25
а
1
а
25
5
; соs
; tg
2
26
2
26
2
1
3.упростите выражение:
1 – cos a . сtg a – sin2 a
1 + cos a
2
соs2 a
4. упростите выражение:
1 – 2 sin2 a + cos2a
2 cos2a
На оглавление
Дальше
52. ПОСТТЕСТ
На «3» решить первые 3 задания.На «4-5» решить соответственно 4 и 5 заданий.
I вариант
II вариант
1. пусть cos a= –0,6 и а – угол III
четверти, найдите sin2a, cos2a, tg2a.
1. пусть tg a= 3/4 и а – угол III
четверти, найдите sin2a, cos2a, tg2a.
2. вычислите 2 sin 15 cos 15
2. вычислите 2 sin 30 cos 30
3. докажите тождество:
(sin a + cos a) – sin 2a = 1
3. докажите тождество:
4 sin a cos a cos 2a = sin 4a.
4. Упростите выражение:
4.упростите выражение:
4 сos a/4 cos (2п + а)/4 cos (2п +а)/2
4 sin a/2 sin (п – а)/2 sin (3п/2 – а)
5. упростите выражение:
sin cos
cos 2 sin 2
На оглавление
5. упростите выражение:
2 sin 2 1
1 2 cos 2
53. Формулы приведения
ЦелиСодержание обучения:
Узнать свойства полупериода синуса и
косинуса.
1. Свойства полупериода синуса и косинуса.
Познакомиться с формулами приведения;
2. Формулы приведения.
Применять формулы для нахождения
тригонометрических функций
На оглавление
Дальше
54. § 1. Свойства полупериода синуса и косинуса
Функции синус и косинус при уменьшении или увеличении аргумента на изменяютсятолько по знаку:
Sina = – sin(a + )
(1)
Cosa = – cos(a + )
(2)
Если к аргументу прибавить , умноженное на любое нечетное число, то получатся формулы:
Sina = – sin[a + (2k+1)]
(3)
Cosa = – cos[a + (2k+1)]
(4)
Т.е. функции синус и косинус при изменении аргумента на (2k+1) изменяются только
по знаку.
На оглавление
Дальше
55. § 2. Формулы приведения
Формулы приведения позволяют выразить тригонометрические функции углов3
, ,
,2 через тригонометрические функции угла .
2
2
Функция
Аргумент
–
(90 – )
(90 + )
2
2
sin
cos
tg
ctg
– sin
cos
– tg
–ctg
cos
sin
ctg
tg
cos
– sin
– ctg
– tg
(180 – )
sin
– cos
– tg
– ctg
(180 + )
– sin
– cos
tg
ctg
На оглавление
Дальше
56. Тренинг. Решение упражнений
Вычислить:1) sin 150 0 ;
2) sin( 120 0 );
0
3) cos 225 ;
4) cos( 240 0 ).
В примерах 1) – 4) используем формулы (1) и (2), а также свойства
четности и нечетности тригонометрических функций:
1) sin 150 0 sin( 150 0 180 0 ) sin( 30 0 ) 1 / 2;
2) sin( 120 0 ) sin( 120 0 180 0 ) sin 60 0
3
;
2
2
;
2
4) cos( 240 0 ) cos( 240 0 180 0 ) cos( 60 0 ) cos 60 0 1 / 2.
3) cos 225 0 cos( 225 0 180 0 ) cos 45 0
Вычислить:
7
1) sin( );
6
2
2) cos( ).
3
7
1
1
) sin( 1 ) sin( ) sin ;
6
6
6
6 2
2
2
1
2) cos( ) cos(
) cos .
3
3
3
2
1) sin(
На оглавление
Дальше
57. ТЕСТ
Вычислить:0
1) sin 135 ;
2)ctg150 0 ;
0
3) cos 70 .
Вычислить:
2
);
3
3
2) cos( ).
4
1) sin(
2
;
2
2) 3 ;
1)
3) sin 20 0.
3
;
2
2
2)
.
2
1)
Вычислить:
1) sin( 810 0 ) cos( 900 0 ) tg( 3950 ) ctg5750 ;
13
17
22
37
2) sin(
) cos(
) tg(
) ctg(
).
6
3
3
4
На оглавление
1) 3;
2) 3 1.
Посттест на «3»
Посттест на «4» и «5»
58. Посттест на «3»
1. Вычислить:cos 2400.
Ответы:
А) -1/2
Б) 1/2
В) 1
59. 2 задание
Вычислить:sin( 23830 ) cos( 4950 ) sin( 20230 ).
Ответы:
2
А)
.
2
Б ) 3.
В) 1 / 2.
60. 2-е задание
Вычислить:sin( 2383 ) cos( 495 ) sin( 2023 ).
0
2
А)
.
2
0
Б ) 3.
0
В) 1 / 2.
61. Посттест на «4» и «5»
Вычислить:1) sin 1200 0 cos 1410 0 3tg930 0.
Упростите:
tg(
2
) ctg ( ) cos(
sin( )
Докажите тождество:
3
1 ctg 2 ( )
tg( )
3
)
2
2
2
1
1 ctg 2 ( 2 )
ctg( )
2
На оглавление
62. Формулы суммы и разности тригонометрических функций
ЦелиСодержание обучения:
Познакомиться с формулами суммы и разностиФормулы суммы и разности
тригонометрических функций;
косинусов (синусов)
Применять формулы для нахождения
тригонометрических функций.
На оглавление
Преобразование произведения
тригонометрических функций в
алгебраическую сумму.
Дальше
63. § 1. Формулы суммы и разности тригонометрических функций.
Сумму и разность синусов и косинусов можно представить в виде произведения.Чтобы представить в виде произведения сумму sin a + sin в, положим а = х+у и
в = х–у и воспользуемся формулами сложения. Получим:
Sin a + sinв = sin (x+y) + sin (x –y) = sinxcosy + cosxsiny + sinxcosy – cosxsiny = 2sinxcos
Из условий а = х + у и в = х– у находим, что х = (а + в) /2 и у = (а – в)/2. Тогда
sin a + sin в = 2 sin (a + в) сos (a – в)
(1)
2
2
получили формулу суммы синусов двух углов.
Аналогично можно вывести формулы разности синусов, суммы и разности косинусов.
sin a – sin в = 2 sin (a – в) сos (a + в)
(2)
2
2
cos a + cos в = 2 cos (a + в) сos (a – в)
(3)
2
2
cos a – cos в = –2 sin (a + в) sin (a – в)
(4)
2
2
На оглавление
Дальше
64.
sin( a b), a k , b k
cos a cos b
2
2
sin( a b)
tga tgb
, a k , b k
cos a cos b
2
2
tga tgb
Часто используются также следующие формулы:
a
;
2
a
1 cos a 2 sin 2 ;
2
1 cos a 2 cos 2
a
);
4 2
a
1 sin a 2 sin 2 ( ).
4 2
1 sin a 2 cos 2 (
На оглавление
Дальше
65. § 2. Преобразование произведения тригонометрических функций в алгебраическую сумму.
1sin cos [sin( ) sin( )];
2
1
cos cos [cos( ) cos( )];
2
1
sin sin [cos( ) cos( )].
2
На оглавление
Дальше
66. Тренинг. Решение упражнений
Алгоритм решенияРешение
упростим сумму:
sin 10 + sin 50
воспользуемся формулой суммы
синусов
sin10+sin50=2sin(10+50)/2cos(10–50)/2
=2sin30cos(–20) = 2 * ½ * cos 20= cos 20
представьте в виде произведения:
cos 0,3п – sin 0,6п
1. sin 0,6п = sin 6п/10 = sin 3п/5,
переведем его в градусы.
2. сos 0,3п тоже переведем в градусы.
3. Представим синус в виде суммы
sin 108 = sin (90+18), разложим по
формуле синуса суммы.
4. Получилось выражение: cos 54 –
cos18, разложим его по формуле разность
косинусов.
5. Упростим выражение и получим:
–2 sin 36 cos 18
sin 3п/5= sin 108
2. cos 0,3п = cos 54
3. sin 108 = sin (90+18)=sin90cos18 +
+cos90 sin18 = cos18, т.к. косинус 90
равен нулю.
4. cos54–cos18= –2sin(54+18)/2*sin(54
–-18)/2
5. cos54–cos18= –2 sin 36 cos 18
1.
2.
На оглавление
1.
Дальше
67. Тест
ЗаданияОтветы
1. разложите на множители
выражение:
a)sin 3a + sin a; б) cos y – cos 3y.
а) 2sin(2a)cosa;
б) –2sin(2y)sin(-y)=2sin(2y)siny
2. представьте в виде
произведения:
sin 15 + cos 65.
Sin15 = sin(90-75) = sin90cos75–
cos90sin75 =
= cos75,
cos75 + cos65 = 2 cos70cos5
3. докажите, что:
sin a sin 2a sin 4a sin 5a
tg3a.
cos a cos 2a cos 4a cos 5a
4. вычислите:
4 sin
8
cos
8
; сos
2
8
sin
2
8
5. проверьте, что:
sin 10 + sin 50 – cos 20 = 0
На оглавление
.
.
2;
2
2
Посттест на «3», «4» и «5»
Выбрать 2 вариант
68. Обратные тригонометрические функции. Построение дуги (угла) по данному значению тригонометрической функции.
ЦелиСодержание обучения:
Узнать обратные тригонометрические функции. 1. Обратные
тригонометрические функции.
Познакомиться со способом построения и
2. Построение дуги (угла) по
нахождением дуги (угла) по данному значению
заданному значению
тригонометрической функции;
тригонометрической функции.
Применять формулы для нахождения дуг (углов).
На оглавление
Дальше
69. § 1. Обратные тригонометрические функции
Функция y = sinx на отрезке [– /2; /2] обратима, т.е. имеет обратную функцию, котораяназывается арксинусом и обозначается y = arcsin x:
D (arcsin x)= [–1; 1], E (arcsin x) = [– /2; /2];
Sin (arcsin x)= x, где х [–1; 1]; arcsin (–x) = – arcsin x.
Функция y = cos x на отрезке [0; ] обратима, т.е. имеет обратную функцию, которая
называется арккосинусом и обозначается y = arccos x:
D (arccos x)= [–1; 1], E (arccos x) = [0; ];
cos (arccos x)= x, где х [–1; 1]; arccos (–x) = – arccos x.
Функция y = tg x на промежутке (– /2; /2) обратима, т.е. имеет обратную функцию,
которая называется арктангенсом и обозначается y = arctg x:
D (arctg x)= R, E (arctg x) = (– /2; /2);
tg (arctg x)= x, где х R; arctg (–x) = – arctg x.
Функция y = ctg x на промежутке (0; ) обратима, т.е. имеет обратную функцию, которая
называется арккотангенсом и обозначается y = arcctg x:
D (arcctg x)= R, E (arcctg x) = (0; );
ctg (arcctg x)= x, где х R; arcctg (–x) = – arcctg x.
На оглавление
Дальше
70. § 2. Построение дуги (угла) по данному значению тригонометрической функции
Найти множество дуг , синус которых равен а.На оси OY единичной окружности построим точку N (0;a)
и проведем через нее прямую, параллельную оси ОХ.
1.
Пусть |а| < 1; тогда прямая y = а пересечет единичную
окружность в точках М1 и М2 (см.рис.), симметричных
относительно оси OY.
Точке М1 соответствует дуга АМ1 = arcsin a, а точке М2
– дуга – arcsin a. Каждая из этих дуг имеет синус
равный а. Множество дуг, оканчивающихся в точке М1 и
имеющих синус, равный а, выражается формулой:
= arcsin a +2 k (k ),
а множество дуг, оканчивающихся в точке М2 и имеющих синус, также равный а,
выражается формулой:
= – arcsin a +2 k (k ),
n
т.к. (–1) = 1 при n = 2k (т.е. если n – четное) и (–1) = –1 при n = 2k +1 (n – нечетное),
то эти две формулы можно объединить в одну: = (–1)n arcsin a + n (n ).
1.
Частные случаи: а) если а = 1, то
На
2
2 k , ( k Z )
б) если а = –1, то 2 k , ( k Z )
2
оглавление
Дальше
71.
2.Найти множество дуг , косинус которых равен а.
На оси OX единичной окружности построим точку N (a;0)
и проведем через нее прямую, параллельную оси ОY.
1. Пусть |а| < 1; тогда прямая x = а пересечет единичную
окружность в точках М1 и М2 (см.рис.), симметричных
относительно оси OX.
Точке М1 соответствует дуга АМ1 = arccos a, а точке М2
– дуга – arccos a. Каждая из этих дуг имеет косинус
равный а. Множество дуг, оканчивающихся в точке М1 и
имеющих косинус, равный а, выражается формулой:
= arccos a +2 k (k ),
а множество дуг, оканчивающихся в точке М2 и имеющих косинус, также равный а,
выражается формулой:
= – arccos a +2 k (k ),
эти две формулы можно объединить в одну:
= arccos a +2 n (n ).
Частные случаи: а) если а = 1, то
2 k , ( k Z )
б) если а = –1, то
На оглавление
2 k , (k Z )
Дальше
72.
3. Найти множество дуг , тангенс которых равен а.На оси тангенсов построим точку N (1;a).Проведем через
эту точку и начало координат прямую, которая пересечет
единичную окружность в точках М1 и М2 (см.рис.).
Тангенс дуг АМ1 и АМ2 равен ординате а точки N –
точке пересечения продолжения радиуса ОМ1 с осью
тангенсов.
Точке М1 соответствует дуга АМ1= arctg a,
а точке М2 соответствует дуга АМ2= arctg a + .
Каждая из этих дуг имеет тангенс равный а.
Множество дуг, оканчивающихся в точках М1 и М2 записывается общей формулой:
= arctg a + n (n ).
На оглавление
Дальше
73.
4. Найти множество дуг , котангенс которых равен а.На оси котангенсов построим точку N (a;1).Проведем через
эту точку и начало координат прямую, которая пересечет
единичную окружность в точках М1 и М2 (см.рис.).
Котангенс дуг АМ1 и АМ2 равен абсциссе а точки N –
точке пересечения продолжения радиуса ОМ1 с осью
котангенсов.
Точке М1 соответствует дуга АМ1= arcctg a,
а точке М2 соответствует дуга АМ2= arcctg a + .
Каждая из этих дуг имеет котангенс равный а.
Множество дуг, оканчивающихся в точках М1 и М2 записывается
общей формулой:
= arсctg a + n (n ).
На оглавление
Дальше
74. Тренинг. Решение упражнений
Алгоритм решенияРешение
Записать главные дуги, синус
которых равен: 1) 0; 2) –1;
3) 1; 4) 3/2; 5) –1/2.
1) = arcsin0 = 0;
2) = arcsin(–1)= –
arcsin1 = – /2;
3) = arcsin1 = /2;
4) = arcsin 3/2 = /3;
5) = arcsin(–1/2) = – arcsin(1/2)= – /6.
Записать множество дуг, синус
которых равен ½.
На окружности имеются две точки, служащие
концами дуг 1 и 2, синус которых равен ½:
1= arcsin1/2 = /6 и 2= – arcsin1/2 = – /6.
Следовательно, искомое множество дуг выражается
формулами: 2 k и 2 k ( 2k 1)
6
6
или ( 1) n 6
n, (n Z )
6
Построить главные дуги arcsin
(2/5) и arcsin (–2/5).
На оглавление
Дальше
75.
Записать главные дуги,косинус которых равен: 1) 0;
2) 1; 3) –1; 4) – 2/2; 5)
1/2.
1) = arccos0 = /2;
2) = arccos1=0;
3) = arccos(–1) = ;
4) = arccos(– 2/2) = – arccos(– 2/2)= –
/4=3 /4 ;
5) = arccos1/2 = /3.
Записать множество дуг,
косинус которых равен ½.
На окружности имеются две точки,
служащие концами дуг 1 и 2, косинус
которых равен ½:
1= arccos1/2 = /3 и 2= – arccos1/2 = – /3.
Следовательно, искомое множество дуг
выражается формулой: .
Построить главные дуги
arccos (2/3) и arccos (–2/3).
На оглавление
Дальше
3
2 n, ( n Z )
76.
Записать главные дуги, тангенскоторых равен: 1) 0; 2) 1; 3)
–1; 4) – 3/3; 5) 3.
1) = arctg0 = 0;
2) = arctg1= /4;
3) = arctg(–1) = –arctg1= – /4;
4) = arctg(– 3/3) = – arctg( 3/3)= – /6 ;
5) = arctg 3= /3.
Записать множество дуг, тангенс
которых равен 3.
На окружности имеются две точки, служащие
концами дуг 1 и 2, тангенс которых равен 3:
1= arctg 3 = /3 и 2= arctg 3+ = /3+ .
Следовательно, искомое множество дуг
выражается формулой: .
n, ( n Z )
3
Построить главные дуги arctg
(4/3) и arctg (– 4/3).
На оглавление
Дальше
77.
Записать главные дуги, котангенскоторых равен:
1) 3/3; 2) –1;
3) 3; 4) –– 3.
1)
= arcctg( 3/3) = /3;
2)
= arcctg(–1)= – arcctg1= – /4=3 /4;
3) = arcctg 3 = /6;
4) = arcctg(– 3)= – arcctg 3= – /6= 5 /6.
Записать множество дуг,
котангенс которых равен 3.
На окружности имеются две точки, служащие
концами дуг 1 и 2, косинус которых равен 3:
1= arcctg 3 = /6 и 2= arcctg 3 + = /6 + .
Следовательно, искомое множество дуг
выражается формулой: .
6
Построить главные дуги arcctg1 и
arcctg (–1).
На оглавление
Дальше
n, ( n Z )
78. Тест
ЗаданияЗаписать главные дуги, синус которых
равен: 1) 1/2; 2) 2/2; 3) – 2/2.
Записать множество дуг, синус которых
равен 3/2.
Ответы
1) /6; 2) /4; 3) – /4.
( 1) k
3
k , ( k Z )
Построить главные дуги arcsin (1/3) и
arcsin (–1/3).
Записать множество дуг, косинус
которых равен 1)–½; 2) 3/2.
Построить главные дуги arccos (4/5) и
arccos (–4/5).
Записать главные дуги, тангенс
которых равен: 1) ½; 2) 3/3; 3) – 3.
На оглавление
1)
2)
2
2 k , ( k Z );
3
6
2 k , ( k Z ).
1)arctg(1/2); 2) /6;
Посттест
3)– /3.
79. Посттест на «3», «4» и «5»
На «3» выполнить первые два задания.На «4» выполнить первые три задания.
На «5» выполнить все задания.
Построить дуги, косинус которых равен (0,6).
Записать множество дуг, тангенс которых равен
1)–1; 2) 3.
Записать главные дуги, котангенс которых
равен 3/3
Вычислить cos(a/2), если cos a= 369
и . 180 a 270
0
На оглавление
0
625
80. Тригонометрические уравнения и тригонометрические неравенства
ЦелиРешать простейшие тригонометрические
уравнения.
Содержание обучения:
Тригонометрические уравнения.
Тригонометрические неравенства.
Решать простейшие тригонометрические
неравенства
На оглавление
Дальше
81. § 1. Тригонометрические уравнения
Простейшими тригонометрическими уравнениями называются уравненияsinx = m, cos x = m, tg x = m, ctg x = m,
где m – данное число.
Решить простейшее тригонометрическое уравнение – значит найти множество всех значений
аргументов (дуг или углов), при которых данная тригонометрическая функция принимает
заданное значение m.
1. Решить уравнение sinx = m.
Решение: Если |m| 1, то на единичной окружности имеются
две дуги arcsin m и – arcsin m, синус которых равен m и
концы которых симметричны относительно оси OY.
Наименьшая по абсолютной величине дуга arcsin m из
промежутка ; , синус которой равен m, называется
2 2
главным решением уравнения sinx = m. Множество всех
искомых дуг, удовлетворяющих уравнению sinx = m, находится прибавлением к
найденным двум дугам любого целого числа периодов синуса:
arcsin m 2 k,
или
х
arcsin m 2 k ,
arcsin m 2 k,
х
arcsin m (2k 1).
Множество корней уравнения можно записать одной формулой:
х = (–1)n arcsin m + n (n ).
На оглавление
Дальше
82.
Если |m|>1, то уравнение решения не имеет.Частные случаи:
1) sinx = –1,
;
х 2 k , ( k Z )
2
2)
sinx = 0,х k , ( k Z )
3)
sinx = 1,х
2
На оглавление
;
2 k , ( k Z )
Дальше
83.
2.Решить уравнение cosx = m.
Решение: Если |m| 1, то на единичной окружности имеются две дуги arccos m и – arccos m,
косинус которых равен m и концы которых симметричны относительно оси OХ.
0;
Наименьшая по абсолютной величине дуга arccos m из промежутка
, косинус которой
равен m, называется главным решением уравнения cosx = m. Множество всех искомых дуг,
удовлетворяющих уравнению cosx = m, находится прибавлением к найденным двум дугам
любого целого числа периодов косинуса
х = arccos m + k (k ).
Если |m|>1, то уравнение решения не имеет.
Частные случаи:
1)
cosx = –1,х 2 k , илих ( 2k 1), k Z
;
2)
3)
cosx = 0,х
k , ( k Z )
2
cosx = 1,х 2 k , ( k Z )
На оглавление
;
Дальше
84.
Решить уравнение tgx = m.Решение: Наименьшая по абсолютной величине дуга arctg m из промежутка 2 ; 2
,
тангенс которой равен m, называется главным решением уравнения tgx = m. Множество
всех искомых дуг, удовлетворяющих уравнению tgx = m, находится прибавлением любого
целого числа периодов тангенса
х = arctg m + k (k ).
3.
Частный случай:
tgx = 0,х k , ( k Z )
4.
Решить уравнение сtgx = m.
Решение: Наименьшая положительная дуга arсctg m из промежутка
, котангенс
0;
которой равен m, называется главным решением уравнения сtgx = m. Множество всех
искомых дуг, удовлетворяющих уравнению сtgx = m, находится прибавлением любого
целого числа периодов котангенса
х = arcсtg m + k (k ).
Частный случай:
сtgx = 0,х k , (k Z )
2
На оглавление
Дальше
85.
§ 2. Тригонометрические неравенства.Простейшими тригонометрическими неравенствами называются неравенства
sinx < m, sinx > m, cos x < m, cosx > m, tg x < m, tgx >m, ctg x < m, ctgx > m,
где m – данное число.
Решить простейшее тригонометрическое неравенство – значит найти множество всех
значений аргументов (дуг или углов), которые обращают данное неравенство в верное
числовое неравенство.
На оглавление
Дальше
86. Тренинг. Решение упражнений
Алгоритм решенияРешение
1) Решить уравнение sinx = ½.
Главным решением является дуга АМ1
= /6 из промежутка ; ,
2 2
синус которой ½.
Множество корней уравнения имеет
вид:
х = (–1)n arcsin 1/2 + n, (n )
х = (–1)n /6 + n, (n ).
2) Решить неравенство: sinx < ½.
Учитывая свойство ограниченности
синуса, данное неравенство можно
переписать так: –1< sinx < ½. Имеем:
АМ1 = /6, АМ2 = – – /6= – 7 /6.
Неравенству sinx < ½ удовлетворяют
дуги из промежутка 7 ; .
6
6
Т.к. синус периодическая функция, то
надо добавить период:
7
2 k ; 2 k , k .
6
6
На оглавление
Дальше
87.
3). Решить неравенство: |sinx| >½.
Это неравенство выполняется
для всех дуг х1 < x < x2 и х3 < x <
x4 , где х1 = /6,
х2 = – /6 = 5 /6,
х3 = х1 + = /6 + ,
х4 = х2+ = 5 /6+ , т.е.
/6 < x< 5 /6, и /6+ < x <
5 /6+ . Общим решением служит
множество дуг вида:
5
, k .
k
k ;
6
6
4)
Решить уравнение cosx = –½.
Главным решением является дуга
АМ1 = – /3=2 /3 из промежутка
0;
косинус которой –½.
Множество корней уравнения
имеет вид:
х = arcсоs(–1/2) + 2 n, (n )
х = 2 /3 + 2 n, (n ).
На оглавление
Дальше
88.
5) Решить неравенство: соsx >– ½.Перепишем данное неравенство
так: –1/2< cosx < 1.
Неравенству cosx >–½
удовлетворяют дуги из
промежутка 2 ; 2 . Общим
3 3
решением будет:
2
2
2 k ;
2 k , k .
3
3
6) Решить неравенство: соsx <– ½.
Перепишем данное неравенство
так: –1 cosx < -1/2. Имеем: АМ1 =
– /3=2 /3, АМ2 = + /3= 4 /3.
Неравенству cosx < –½
удовлетворяют дуги из
2 4
промежутка 3 ; 3
. Т.к.
косинус периодическая функция,
то:
4
2
2 k ;
2 k
3
3
, k .
На оглавление
Дальше
89.
7) Решить неравенство: |соsx| > 2/2.Это неравенство выполняется для всех дуг х1 < x < x2 и
х3 < x < x4 , где х1 = /4,
х2 = – /4,
х3 = х1 + = /4 + ,
х4 = х2 – = – /4 – , т.е. для
– /4 < x< /4, и – /4– < x < /4+ .
Общим решением служит множество дуг вида:
k ; k
4
4
, k .
8) Решить уравнение tgx = 3.
Главным решением является дуга /3 из промежутка 2 ; 2
тангенс которой равен 3. Множество корней уравнения
имеет вид: х= /3+ k, k .
9) Решить неравенство: tgx > 3.
Учитывая свойство неограниченности тангенса, запишем
3< tgx <+ . Неравенству
tgx > 3 удовлетворяют дуги из
;
промежутка: 3 2 , учитывая период:
k ; k
2
3
На оглавление
, k .
Дальше
90.
10) Решить уравнение сtgx = –1.Главным решением является дуга – /4=3 /4
из промежутка 0; , котангенс которой
равен –1. Множество корней уравнения имеет
вид: х=3 /4+ k, k .
11) Решите неравенство ctgx >1.
Учитывая свойство неограниченности
котангенса, запишем 1< сtgx <+ .
Неравенству сtgx > 1 удовлетворяют дуги из
промежутка: 0; , учитывая период:
4
k
;
k , k .
4
На оглавление
Дальше
91. Тест
ЗаданияОтветы
Решить уравнение sinx = 2/2;
х = (–1)n /4 + n, (n ).
Решите неравенства: 1) |sinx|<1/2;
2)sinx >– 3/2.
1)
Решить уравнение 1)cosx = – 2/2;
2) cosx = 3/2;
Решите неравенства: 1) |cosx|<1/2;
2)cosx >–1.
Решить уравнение tgx = – 3/3
Решите неравенство tgx<– 3
На оглавление
k ; k
6
6
, k .;
4
2 k ;
2 k
2) 3
3
, k .
1) х = 3 /4 + 2 n, (n ).
2) х = /6 + 2 n, (n ).
1)
2
k
k ;
3
3
, k .;
2) 2 k ;2 k , k .
6
k
, k
k ; k , k .
3
2
Дальше
92. Посттест
На «3» решить по 2 любых уравнения и неравенства (без построений), (всего 4 примера).На «4» решить по три любых уравнения и неравенства (можно уравнения без построений),
(всего 6 примеров).
На «5» выполнить все с построениями.
Решить уравнения
1) sinx = – 3/2;
2) cosx = 1/2;
3)
tgx = 1;
4) ctgx = 3.
Решите неравенства
1) sinx < – 3/2;
2) cosx < 1/2;
3) |tgx| < 3;
4) |ctgx| < 1.
На оглавление
93. Решение тригонометрических уравнений и тригонометрических неравенств
Цели1. Решать тригонометрические уравнения.
Содержание обучения:
Примеры решения различных
тригонометрических уравнений.
2. Решать тригонометрические неравенства
Примеры решения различных
тригонометрических неравенств
На оглавление
Дальше
94. § 1. Примеры решения различных тригонометрических уравнений
1.Решить уравнение sin2 x = m.(0 m 1)
Решение: Данное уравнение сводится к двум простейшим уравнениям
sinx = m и sinx = – m. Записав решение каждого из них по общей формуле, получим:
х k ( 1) k arcsin m
и .х k ( 1) k arcsin m
Множество корней уравнения можно записать одной формулой:
х = n arcsin m , (n ).
2.
Решить уравнение cos2 x = m.(0 m 1)
Решение: Данное уравнение сводится к двум простейшим уравнениям cosx = m и cosx = – m.
Записав решение каждого из них по общей формуле, получим
х 2 k arccos m хи . 2 k ( arccos m ) (2k 1) arccos m
Множество корней уравнения можно записать одной формулой:
х = n arccos m , (n ).
На оглавление
Дальше
95.
3. Решить уравнение tg2 x = m.Решение: Данное уравнение сводится к двум простейшим уравнениям tgx = m и tgx = – m.
Записав решение каждого из них по общей формуле, получим:
х k arctg m и х. k arctg m
Множество корней уравнения можно записать одной формулой:
х = k arctg m , (k ).
4.
Решить уравнение ctg2 x = m.
Решение: Данное уравнение сводится к двум простейшим уравнениям сtgx = m и сtgx = – m
Записав решение каждого из них по общей формуле, получим:
х k arcсtg m
и .х k arcсtg m
Множество корней уравнения можно записать одной формулой:
х = k arcсtg m , (k ).
На оглавление
Дальше
96. § 2. Примеры решения различных тригонометрических неравенств
sin1)
3
х 1
2 2
4 k x
6
5
4 k ;
3
tg 2 x 1
2)
4
k
2
х 5
2 k ;
домножим выражение на 2:
2 6
5
или х ( 3 4 k ; 3 4 k )
, k .
. Имеем: 2 k
x
k 2 х k ;
. Имеем:
2
4
8
k
2
;
На оглавление
или х (
4
k
2
;
разделим все выражение на 2:
8
k
2
).
Дальше
97. Тренинг. Решение упражнений
Алгоритм решенияРешение
1) Решить уравнение sin2x = ½.
2х = (–1)n arcsin 1/2 + n, (n )
2х = (–1)n /6 + n, (n ). Разделим выражение
на 2.
Множество корней уравнения имеет
вид:
х = (–1)n /12 + n/2, (n ).
2)
Решить уравнение tg(3x + 2)= –1.
3х 2
3x
3)
4
4
k ;
2 k ;
Решить уравнение ctg x2 =0
х2
2
| k |,
4) Решить уравнение cos(cosx) = ½.
х = arcсоs(1/2) + 2 n, (n )
х = /3 + 2 n, (n ).
На оглавление
Множество корней уравнения имеет
вид:
2 k
x
;
(k ).
12
3
3
Множество корней уравнения имеет
вид:
х
| k |,
(k ).
2
Это уравнение не имеет корней, т.к.
при любом k его правая часть
превосходит единицу по
абсолютной величине.
Дальше
98.
Решить уравнение 2. sin 2 х 7 sin x 3 0Сделаем замену: sinx = t. Имеем:
2 t2 – 7 t + 3 = 0. Данное квадратное
уравнение решаем относительно t.
Получаем корни: t1 = ½; t2 = 3.
Возвращаемся к исходной величине: sinx1 = ½;
sin x2 = 3.
sin x = ½; х = (–1)n /6 + n, (n )
Уравнение sinx = 3 решения не имеет, т.к.
область значений [–1;1].
6)Решить уравнение 4соs 2 х sin x 1 0
Воспользуемся тригонометрическим
2
тождеством и получим: 4(1 sin х) sin x 1 0 ,
после преобразования имеем: 4 sin 2 х sin x 3 0
Решаем аналогично предыдущему и получаем:
sin x = – ¾ и sin x = 1.
Множество корней данного
уравнения имеет вид:
х = (–1)n /6 + n, (n )
7) Решить уравнение 3. сtg3х tg3x 3 0
Из определения tgx и сtgx, знаем, что
знаменатели sin3x и cos 3x. Знаменатель не
должен быть равен 0, поэтому: 3х k , 3x
/2+ k, т.е. x k/3, x /6+ k/3. Заменяя ctg3x
на 1/tg3x, получим:
1
2
Множество корней данного
уравнения имеет вид:
пk пk
1
5)
2
На оглавление
tg3x
Множество корней данного
уравнения имеет вид:
х = (–1)n+1 arcsin3/4 + n, (n ) и
х = /2 + n, (n )
;
k Z
arctg 2
3 12 3
3
tg3x 3 0; tg 3x 3tg3x 2 0;
1
пk
tg3x 2,3x arctg 2 k , x arctg 2
;
3
3
пk
tg3x 1,3x k , x
4
12 3
Дальше
99.
tgх cos x tgx cos x 1 08)
Решить уравнение
.
По определению тангенса в знаменателе
cosx 0, x /2+ k. Разложим левую часть на
множители, а затем приравняем каждый из
сомножителей к нулю:
Уравнению удовлетворяет
множество корней вида:
(2k 1), x k | k Z
4
tgx(cos x 1) (cos x 1) 0; (cos x 1)(tgx 1) 0;
cos x 1 0, cos x 1, x (2k 1)
tgx 1 0, tgx 1, x
4
k
tg 3. х tgx
9)
Решить уравнение
По определению тангенса в знаменателе
cosx 0, x /2+ k. Имеем:
Уравнению удовлетворяет
множество корней вида:
k , x k | k Z
4
tg 3 х tgx 0, tgx(tg 2 x 1) 0, tgx 0, tg 2 x 1 0
х k , x
10)
4
k.
Решить уравнение
sin х сosx 0
Имеем sin х сosx,
sin х
1
сosx
,
.
x
4
k | k Z
сosx 0, ( х / 2 k ), tgx 1
На оглавление
Дальше
100.
11) Решить уравнениеsin. 2 х 4 sin xсosx 3 cos 2 х 0
Поделим все слагаемые на cos2 x, получим:
sin 2 х 4 sin xсosx 3 cos 2 х
0; ( х k ),
2
2
2
2
cos х
cos х
cos х
2
tg х 4tgx 3 0,
k , k Z
4
x arctg 3 k , k Z
х
решаем его аналогично 5) и 6) примерам,
получим: tgx = 1; tg x = 3.
х
4
k , x arctg 3 k , k Z
2 sin 2 х 5 sin xсosx cos 2 х 4 0
12) Решить уравнение
.Свободный член можно представить как 4*1,
где 1 разложить по основному
тригонометрическому тождеству. Получим:
. 2 sin 2 х 5 sin xсosx cos 2 х 4(sin 2 х соs 2 х) 0
После преобразований получим однородное
уравнение: 2 sin 2 х 5 sin xсosx 3 cos 2 х 0
Поделим все слагаемые на cos2 x, получим:
решаем его аналогично 5) и 6) примерам,
получим: 2 sin 2 х 5 sin xсosx 3 cos 2 х
х
4
k , x arctg
0; ( х k ),
2
cos 2 х
cos 2 х
cos 2 х
2
2tg х 5tgx 3 0,
tgx = 1; tg x = 3/2.х k , k Z
4
x arctg
3
k , k Z
2
На оглавление
Дальше
3
k , k Z
2
101. Тест
ЗаданияРешить уравнения:
х
1
sin(
1) 2 6 ) 4
2) tg(3x + 1) = 1;
3) sin(cosx)=0.
Решите неравенства:
1)
sin2x < –1/2;
2)
cos(x/2) >–1/2;
Решить уравнение
1) sin2 x = 1/2;
2) tg2 x = 1;
3) ctg2 x = 3.
Решить уравнения:
1) 2 sin 2 х 3 sin x 3 0
;
2) 2 sin х 3соsx 0
;
2
2
3) sin х 6 sin xсоsx 5 cos х 0
;
2
2
4) 9 sin х 32 sin xсоsx 25 cos х 25. ;
На оглавление
Ответы
1) х = 2(–1)n arcsin(1/4)– /3 + 2 n,
(n );
2) х = /12 – 1/3 + n/3, (n );
3)
1) 5 k ; k , k .;
2)
12
12
4
4
4 k ;
4 k
3
3
1)
2)
3)
х = /4 + n, (n ).
х = /4 + n, (n ).
х = /6 + n, (n ).
1)
2 k ;
, k .
2 k
3
, k .
x arctg1,5 k , k Z
2)
;
k , arctg 5 k | k Z
3)
4
4) k , arctg 2 k | k Z ;
;
Посттест (выбрать 3 вариант)
102. Смешанные задания
ЦелиПовторить:
1. Решение тригонометрических уравнений.
2. Решение тригонометрических неравенств.
3. Основные формулы.
4. Правила упрощения выражений.
5. Правила доказательства тождеств.
На оглавление
Дальше
103. Тренинг. Решение упражнений
34
3 3 4 4
1)
sin(arcsin arcsin ) sin( ) sin cos cos sin 1
5
5
5 5
5 5
[обозначим arcsin3/5= и arcsin4/5= , имеем sin =3/5, [– /2; /2] и sin =4/5, [– /2; /2].
Находим cos = 1– (3/5)2 = 4/5 и cos = 1– (4/5)2 =3/5.]
3
8
2)
cos(arccos arcsin )
5
17
[обозначим arccos3/5= и arcsin8/17= , имеем cos =3/5, [0; ] и sin =8/17, [– /2; /2].
Находим sin = 1– (3/5)2 = 4/5 и cos = 1– (8/17)2 =15/17] =
cos( ) cos cos sin sin
3 15 4 8 13
5 17 5 17 85
1
3
tgarctg
1
3
2
2 1/ 2 3 / 2 8
tg (arctg arctg )
3)
1
3 1 (1 / 2) (3 / 2)
2
2
1 tgarctg tgarctg
2
2
tgarctg
4
[обозначим arcsin4/5= и arctg3= , имеем sin =4/5,
arctg 3)
5
[– /2; /2] и tg =3, (– /2; /2). Находим ctg = 4/3 и ctg = 1/3]
4)
сtg (arcsin
4 / 3 1/ 3 1
1
ctg
(
)
=
4 / 3 1/ 3
3
На оглавление
Дальше
104.
5)Решить уравнения:
А) sin( х ) cos( x) 1 0 cos х cos x 1 0 cos х 2 cos 2 х 0
2
2
2
2 2
х
х
х
или 1 2 cos х 0;
cos (1 2 cos ) 0 cos 0
2
2
2
2
х
х
0, k , x (2k 1);
2
2 2
х
х
1 х
2
4
4
1 2 cos 0; cos ,
2 k , x
4 k , x
(3k 1).
2
2
2 2
3
3
3
cos
4
(3k 1) | k Z
3
х
х
х
х
х
х
Б) sin x cos x 1 sin x 1 cos x 2 sin cos 2 sin 2 2 sin (cos sin ) 0
2
2
2
2
2
2
х
х
х
sin 0 или соs sin 0 второе уравнение поделим на косинус половинного угла:
2
2
2
Уравнению удовлетворяет множество корней вида (2k 1); x
sin
х
х
0 или tg 0
2
2
х
х
0; k ; x 2 k ;
2
2
х
х
tg 1; k ; х 2 k .
2
2 4
2
sin
Уравнению удовлетворяет множество корней вида 2 k ; 2 k | k Z
На оглавление
2
Дальше
105.
2zВ) 3 sin x + 4 cos 2x = 4. Выразим sin x и cos x через z = tg(x/2); имеем
, x 1 z .
sin x
cos
2
1 z
1 z2
Тогда 6 z 2 4 4 z2 4;4 z 2 3z 0; z1 0, z 2 3
.
2
1 z
1 z
4
Данное уравнение равносильно совокупности уравнений tg(x/2)=0 и tg(x/2)=3/4,
откуда х/2= k и х/2=arctg(3/4)+ k. Уравнению удовлетворяет множество корней вида
3
2 k ;2arctg 2 k | k Z
4
6) Преобразовать в произведение:
sin 2 cos 3 2 sin 2 sin 3
sin 2 cos 3 2 sin 2 sin 3 2 sin cos cos 3 2 sin 2 sin 3
2 sin (cos cos 3 sin sin 3 ) 2 sin соs 4
7) Доказать тождество:
sin sin 2 sin 4 sin 5
tg3
. cos cos 2 cos 4 cos 5
(sin 5 sin ) (sin 4 sin 2 ) 2 sin 3 соs 2 2 sin 3 соs 2 sin 3 (соs 2 соs )
(cos 5 cos ) (cos 4 cos 2 ) 2соs3 соs 2 2соs3 соs 2соs3 (соs 2 соs )
tg3
1)
2) sin 47 0 sin 610 sin 110 sin 25 0 4 cos 7 0 соs36 0 sin 18 0
(sin 47 0 sin 610 ) (sin 110 sin 25 0 ) 2 sin 54 0 cos 7 0 2 sin 18 0 cos 7 0
2 cos 7 0 (sin 54 0 sin 18 0 ) 4 cos 7 0 соs36 0 sin 18 0
На оглавление
Дальше
106. Тест
ЗаданияОтветы
Вычислите:
1)cos(arccos 1 arcсоs 11 );
7
2)
sin(arcsin
1)
2)
14
71/98;
1.
5
12
arcsin )
13
13
Решите уравнения:
х
1)1 соsx sin
2
х
2) 1 соsx соs
2
Преобразуйте в произведение:
1)sin cos 2 sin 2 sin
2
2) sin 10 0 2 sin 5 0 cos 15 0 сos50 0
1)
k
2 k
2 k ; (1)
2)
(2k 1);
1)
2 sin
2)
2
3
2
(6k 1) | k Z
3
cos(
2
);
сos10 0
Докажите тождество:
1)
sin sin 3 sin 5 sin 7
сtg
cos cos 3 cos 5 cos 7
На оглавление
, k .
Дальше
107. Посттест
По количеству выполненных заданий выставляется соответствующая оценка. (1 задание – «3»)Докажите тождество:
2 sin x sin 2 x
2 х
ctg
;
2 sin x sin 2 x
2
Решите уравнение:
3 sin x 2 cos 2 х.
Докажите тождество:
4 sin 25 0 sin 65 0
2;
0
соs 40
На оглавление
108. Смешанные задания
ЦелиПовторить:
Решение тригонометрических уравнений.
Решение тригонометрических неравенств.
Основные формулы.
Правила упрощения выражений.
Правила доказательства тождеств
На оглавление
Дальше
109. Тренинг. Решение упражнений
1) Вычислите значения sin3x, cos3x, tg3x и ctg3x, если sinx = ½, угол принадлежит I четвертФормула для вычисления sin3x = 3sinx – 4 sin3 x:
sin3x = 3*1/2 – 4*(1/2)3 = 1,5 – 0,5 = 1;
Формула для вычисления cos3x = 4 cos3 x – 3cosx:
cosх = 1 – sin2 x = 1 – ¼ = 3/2;
cos3x = 4*3 3/8 – 3* 3/2 = 0.
Формула для вычисления tg3x = sin3x/cos3x:
tg3x не существует.
Формула для вычисления ctg3x = cos3x/sin3x:
ctg3x = 0.
3
3
2)
Упростите выражение:
=
cos(
)tg ( ) sin( ) ctg (
) ctg ( )
2
2
2
2
2
sin ctg cos tg tg 0
=
ctg ( )
3)
Доказать тождество: sin( )
cos( 2 )
2
1)
sin
tg ( )
sin( )
tg ( )
2
ctg ( )
sin( )
cos(2 ) sin tg
cos
cos
2
sin
tg ( )
sin( )
tg сtg sin сtg
tg ( )
2
На оглавление
Дальше
110. Тест
ЗаданияОтветы
– 3/2
Вычислите:
1
3
sin( arcсоs ( ) 3 arcsin
)
2
2
Решите уравнение:
sin 2x соsx сos3x
2
k
2
, k .
Преобразуйте в произведение:
sin 80 0 sin 30 0
2 sin 55 0 cos 25 0 ;
Докажите тождество:
3
)
2
1)
ctg 2 ( 2 )
sin 2 (
sin 2 ( )
1
3
2
ctg ( )
2
На оглавление
Дальше
111. Посттест
По количеству выполненных заданий выставляется соответствующая оценкаДокажите тождество:
1 соsx соs2 x сos3x
2cоsx;
2
2соs x соsx 1
Решите уравнение:
sin 2 x sin x cos х 0.
Дано: sina=0,8, sinb=0,96, а Iчетверти,
b Iчетверти.
Найти sin(a – b).
На оглавление












































































































 Математика
Математика