Анаграммы. Урок алгебры в 8 классе

1.

Урок алгебры в 8 классе

2. Анаграммы

• таиимдкисрнн
• ретокоз
• ниваренуе
• фэкоцинетиф
• ерокнь
Дискриминант
Отрезок
Уравнение
Коэффициент
Корень
Ответы:
2

3.

08.02.17г.
Тема урока:
Решение квадратных уравнений
3

4. Разминка

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Разминка
Какое название имеет уравнение второй степени?
От чего зависит количество корней квадратного
уравнения?
Сколько корней имеет квадратное уравнение, если D
больше 0?
Равенство с переменной?
Соперник нолика?
Очень плохая оценка знаний?
Что значит решить уравнение?
Как называется квадратное уравнение, у которого первый
коэффициент 1?
Как называется квадратное уравнение, у которого второй
коэффициент и свободный член =0?
Сколько корней имеет квадратное уравнение, если
дискриминант меньше 0?
4

5. Проверь себя:

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Квадратное
От дискриминанта
2
Уравнение
Крестик
2
Найти его корни, или доказать, что их нет
Приведенное
Неполное
Не имеет корней
5

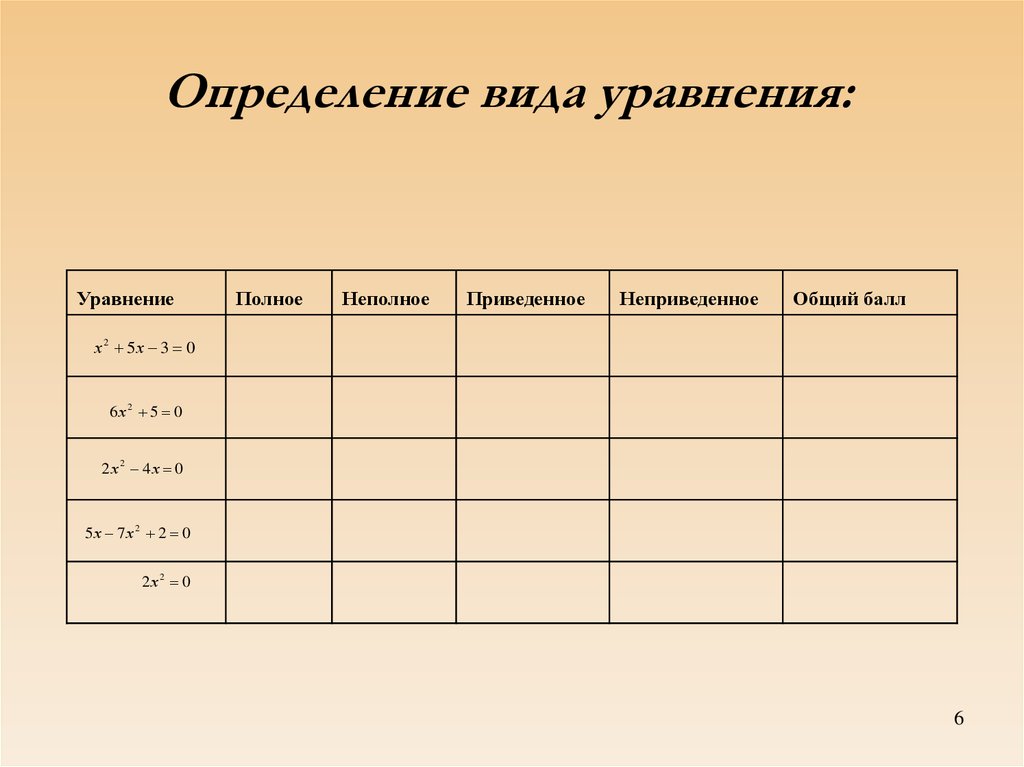
6. Определение вида уравнения:

Уравнение
Полное
Неполное
Приведенное
Неприведенное
Общий балл
х 2 5х 3 0
6х 2 5 0
2х 2 4х 0
5х 7 х 2 2 0
2х 2 0
6

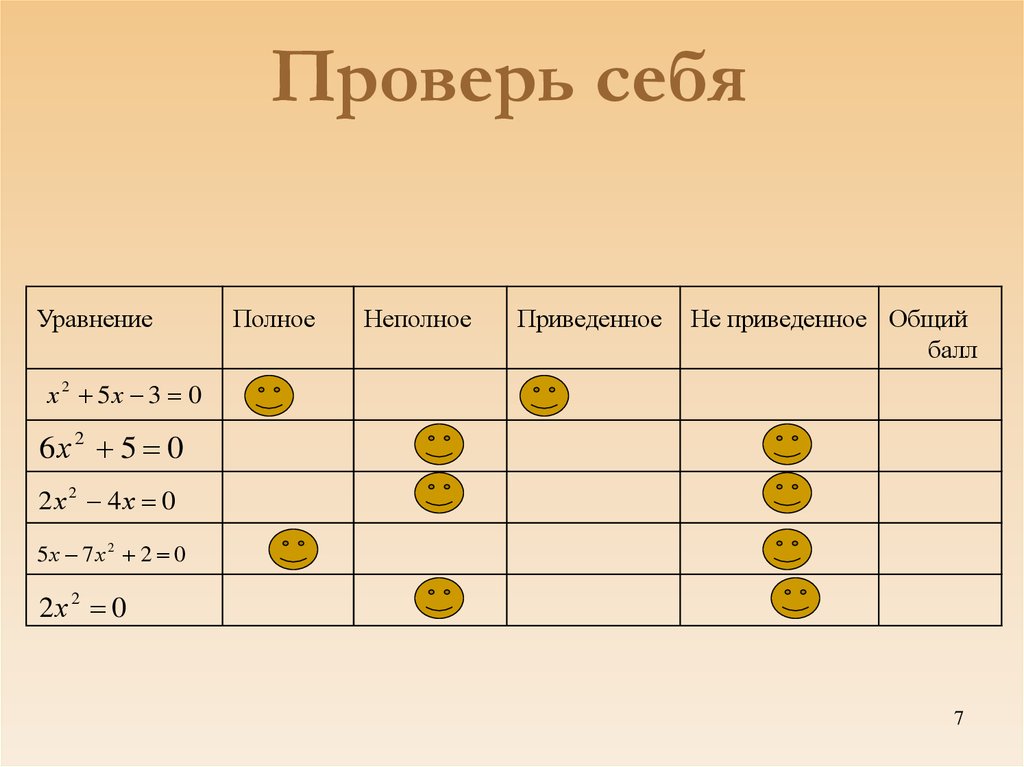
7. Проверь себя

Уравнение
Полное
Неполное
Приведенное
Не приведенное Общий
балл
х 2 5х 3 0
6х 2 5 0
2х 2 4х 0
5х 7 х 2 2 0
2х 2 0
7

8.

Проверь решение и исправь
ошибки.
1)х2 – x - 12 = 0
Решение: D = b2 – 4 ac
D = -12 - 4∙1∙(- 12) = - 49 нет
корней
8

9. Немного истории

Квадратные уравнения возникли очень давно. Еще в
Вавилоне около 2000 лет назад до нашей эры. В 1202
году итальянский ученый Леонард Фибоначчи
изложил формулы квадратного уравнения.
9

10. Немного истории

В
17
веке,
благодаря
И.Ньютону и Р.Декарту способы
решения квадратных уравнений
приняли современный вид.
Исаак Ньютон,
Рене Декарт,
(1643-1727гг.)
(1596-1650гг.)
10

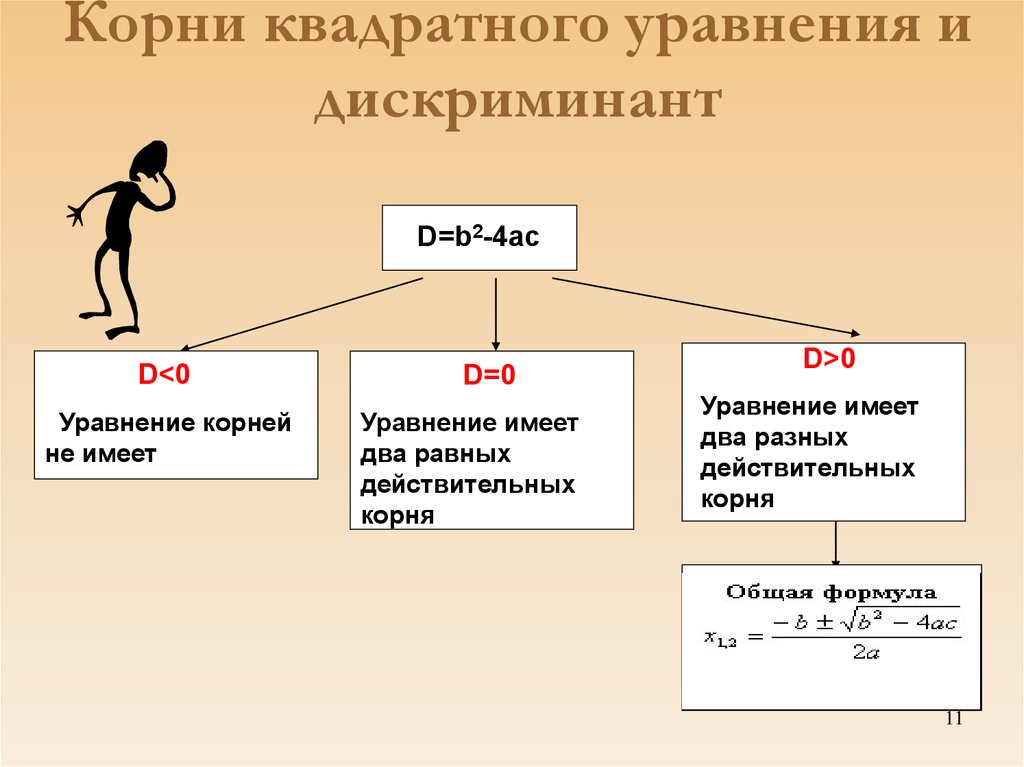
11. Корни квадратного уравнения и дискриминант

D=b2-4ac
D<0
Уравнение корней
не имеет
D=0
Уравнение имеет
два равных
действительных
корня
D>0
Уравнение имеет
два разных
действительных
корня
11

12.

Работа в парах. Какой цветок
изображен на слайде?
1.3x2+7x + 2 = 0
(……..) 1 -2;
2
2.5х -6х3 + 1 = 0
(……..)
3. 2х2 +5х-7 = 0
(….…)
4. 4х2 +4х-3 = 0
(…….)
Р
О
З
А
Ключ
0
а
в
р
3
1;
0,2
0,5;
-1,5
-1;
3
-2;
1;
-3,5
1
3
12

13.

Роза
о которой в народе говорят:
“Цветы ангельские, а когти
дьявольские”.
Легенда о розе:
по словам Анакреона, родилась
роза из белоснежной пены,
покрывающей тело Афродиты,
когда богиня любви выходила из
моря. Поначалу роза была
белой, но от капельки крови
богини, уколовшейся о шип,
стала алой.
13

14. Физкультминутка

*
14

15. Реши уравнение

• 3x2 -14x +11 = 0
• 4x2 + 5x +1 = 0
15

16. Решение квадратных уравнений по свойству коэффициентов

Решение квадратных уравнений
по свойству коэффициентов
• Свойство 1
Если а + b + с = 0 (т.е. сумма коэффициентов
уравнения равна нулю), то
х1= 1, х2 = с/а
• Свойство 2
Если а – b + с = 0, или b = а + с, то
х1 = – 1, х2 = – с/а
16

17. Примеры

Уравнения
Сумма
Корни
коэффициентов
а+в+с
2 х 2 5х 3 0
2–5+3=0
5х 2 8х 3 0 5 – 8 + 3 = 0
ах 2 вх с 0 а + в + с = 0
х 1,
х 1,5
х 1,
х 0,6.
х 1,
х с
а
17

18. Решите самостоятельно

1 вариант
1. 10х2-24х+14=0
2. 2х2+2015х-2017=0
х1 1, х2
1.
2. х
• 2 вариант
1. 6х2-14х+8=0
2. 2х2+2017х+2019=0
Проверь себя:
2
х
1
1.
5
1 1, х2 1008,5
1
1 1, х2 1
3
2.х 1,
1
2
х 1009,5
18

19. Домашнее задание

1. п.22, п.23 №541(а, в, д.)
2. Составить два уравнения ,
используя
свойства
коэффициентов .
3. Составить кроссворд по теме
«Квадратные уравнения»»
19

20.

«Человеку,
изучающему
алгебру,
часто полезнее решить одну и ту же
задачу тремя различными способами, чем
решить три-четыре различные задачи.
Решая одну задачу различными методами,
можно путем сравнений выяснить, какой
из них короче и эффективнее. Так
вырабатывается опыт»
(У. Сойер)
20

21.

21