Похожие презентации:
Плоскость. Уравнение плоскости по точке и нормальному вектору
1. ПЛОСКОСТЬ. УРАВНЕНИЕ ПЛОСКОСТИ ПО ТОЧКЕ И НОРМАЛЬНОМУ ВЕКТОРУ
Положениеплоскости в
пространстве вполне
определяется заданием
любых
трех точек, не лежащих
на одной прямой;
точки плоскости и вектора
перпендикулярного этой
плоскости.
2.
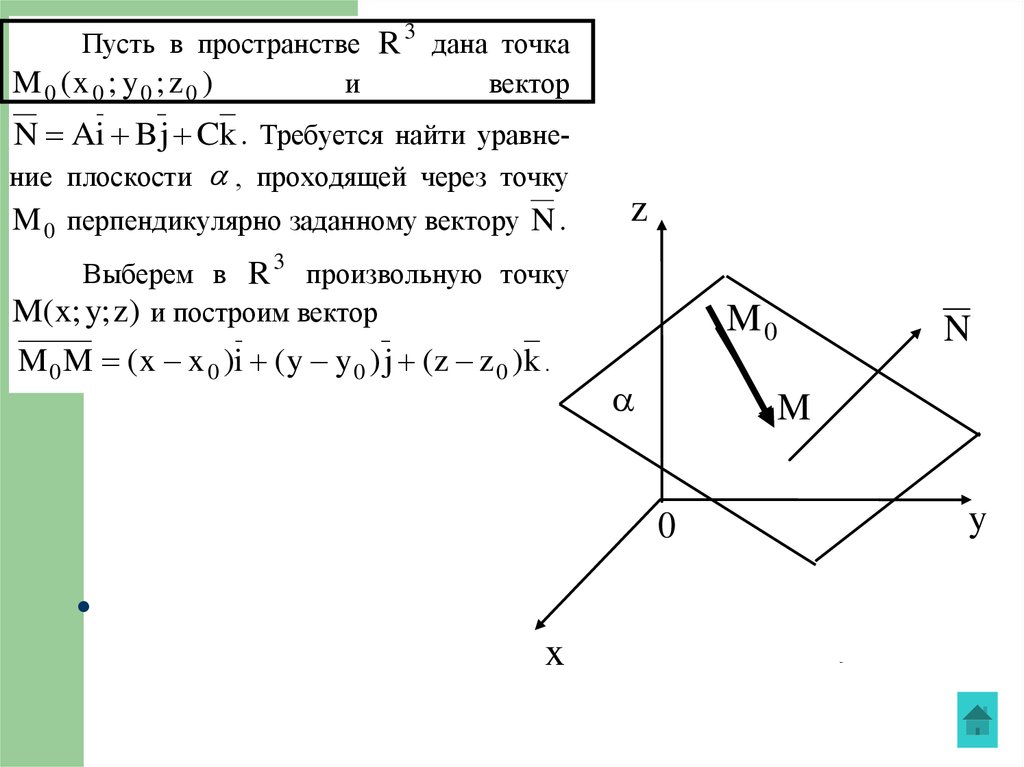
Пусть в пространстве R 3 дана точкаM 0 (x 0 ; y 0 ; z 0 )
и
вектор
N Ai B j Ck . Требуется найти уравнение плоскости , проходящей через точку
M 0 перпендикулярно заданному вектору N .
z
Выберем в R 3 произвольную точку
M(x; y; z) и построим вектор
M 0 M ( x x 0 )i ( y y 0 ) j (z z 0 )k .
M0
M
y
0
x
N
Рис. 1.21
3.
Рассмотрим два случая:1) если
точка
M
M 0 M N N M 0 M 0
A( x x 0 ) B( y y 0 ) C(z z 0 ) 0
то
2) если точка M , то вектора M 0 M и N не
перпендикулярны.
N M 0 M 0 A( x x 0 ) B( y y 0 ) C(z z 0 )
Из случаев 1) и 2) и определения уравнения поверхности следует, что уравнение п.1 есть уравнение
искомой плоскости . Данное уравнение называется
уравнением плоскости по точке и нормальному вектору. Вектор N , перпендикулярный плоскости , называется нормальным вектором этой плоскости.
4.
ПРИМЕР. Составить уравнение плоскости, проходящей че-рез точку M 0 (5; 1;3) перпендикулярно вектору N 2;3;4 .
Решение. Уравнение искомой плоскости будем искать в
форме
A( x x 0 ) B( y y 0 ) C(z z 0 ) 0 . Полагая в уравнении (1.35)
A 2, B 3, C 4, x 0 5, y 0 1, z 0 3 получим
2(x 5) 3( y 1) 4(z 3) 0 2x 3y 4z 19 0.
5. УРАВНЕНИЕ ПЛОСКОСТИ ПО ТРЕМ ТОЧКАМ
Пусть в пространстве R 3 даны триточки
M1 ( x1 ; y1 ; z1 ), M 2 ( x 2 ; y 2 ; z 2 ), M 3 ( x 3 ; y 3 ; z 3 ) не
лежащие на одной прямой. Выберем в
этом пространстве произвольную точку
M(x; y; z) и построим три вектора
z
M
M1M x x1 ; y y1 ; z z1
M1M 2 x 2 x1 ; y 2 y1 ; z 2 z1
M1M 3 x 3 x1 ; y 3 y1 ; z 3 z1
M2
M1
M3
y
0
Рис. 1.22
x
6.
M лежит на плоскости проходящей через заданные точки M 1 , M 2 , M 3 . Тогда векторы M1M, M1M 2 и M1M 3 лежат на этойплоскости. Следовательно, (M1M M1M 2 ) M1M 3 0
Предположим, что точка
x x1
y y1
z z1
x 2 x1
y 2 y1
z 2 z1 0 .
x 3 x1
y 3 y1
z 3 z1
Если же точка M , то векторы M1M, M1M 2 и M1M 3 не
компланарны. Тогда и их смешанное произведение отлично от нуля.
Согласно определению, данное уравнение является уравнением искомой плоскости .
Заметим, что если расписать определитель, то полученное уравнение так же, как и уравнение, будет алгебраическим уравнением
первой степени относительно трех переменных x, y, z .
7. ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
Уравнение Ax By Cz D 0 называетсяобщим уравнением плоскости.
Рассмотрим некоторые частные случаи этого уравнения:
1) D 0 . Тогда, плоскость Ax By Cz 0 проходит через
начало координат, так как точка O(0;0;0) принадлежит этой плоскости
при любых значениях A, B и C ;
2) C 0 . Уравнение плоскости запишется в виде
Ax By D 0 . Так как старшие коэффициенты A, B и C являются
проекциями нормального к плоскости вектора N , то вектор
N A; B;0 перпендикулярен этой плоскости. Но вектор N перпендикулярен и координатной оси OZ. Следовательно, рассматриваемая
плоскость параллельна оси OZ ;
8.
3)если
B 0,
то
плоскость
Ax Cz D 0 параллельна оси OY (доказать
самостоятельно);
4) если A D 0 , то плоскость проходит
через начало координат и параллельна оси OX .
Следовательно, плоскость
By Cz 0 проходит через ось OX ;
5) если A B D 0 , то Cz 0 z 0
совпадает с плоскостью XOY .
9.
ПРИМЕР. Определить, перпендикулярен ли векторa 3;0;4 плоскости 2x 5y z 1 0.
Решение. Коэффициенты A 2, B 5, C 1 являются
проекциями нормального вектора N плоскости. Тогда,
если вектор a перпендикулярен заданной плоскости, то
векторы N и a должны быть коллинеарными. Согласно
условию коллинеарности двух векторов проекции этих
векторов должны быть пропорциональными между собой.
3
0
Но
, следовательно, вектор a не перпендикуля2 ( 5)
рен данной плоскости.
10. УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Пусть в R 3 заданы своими уравнениями две плоскости1 : A1x B1 y C1z D1 0 и 2 : A 2 x B2 y C 2 z D 2 0
z
N1
N2
2
1
y
0
Рис. 1.23
x
11.
Коэффициенты A, B и C уравнения плоскости являются проекциями нормального вектора N к этой плоскости. Следовательно,один из смежных двугранных углов между плоскостями 1 и 2
равен углу между нормальными к этим плоскостям векторами
N1 А1 ; B1 ; C1 и N 2 А 2 ; B2 ; C 2 .
Тогда
cos
N1 N 2
N1 N 2
A1A 2 B1B 2 C1C 2
A1 2 B1 2 C1 2 A 2 2 B 2 2 C 2 2
.
По данной формуле определяется один из смежных двугранных
углов между данными плоскостями.
12.
Следствие 1. Если плоскости 1 и 2 параллельны, то их нормальные векторы N1 и N 2 коллинеарны. ТогдаA1 B1 C1
.
A2 B2 C2
Данные условия называются условиями параллельности двух
плоскостей.
Следствие 2. Если плоскости 1 и 2 перпендикулярны, то в
угол . Тогда cos 0. Следовательно, и
2
A1A 2 B1B 2 C1C 2 0 .
Данное условие называется условием перпендикулярности двух
плоскостей.
13.
Определить,при
каком
значении
плоскость
3x 5y z 3 0 перпендикулярна плоскости x 3y 2z 5 0 .
ПРИМЕР.
Решение. Векторы N1 3; 5; , N 2 1;3;2 являются нормальными
векторами к данным плоскостям. Тогда согласно условию плоскости взаимно
перпендикулярны, если
3 1 ( 5) 3 2 0 2 12 6. Ответ: 6.
ПРИМЕР. Составить уравнение плоскости, которая проходит через точку
M 0 (3; 2; 7) параллельно плоскости 2x 3z 5 0.
Решение. Искомая плоскость проходит через заданную точку M 0 , тогда
ее уравнение, запишется в виде:
A(x 3) B( y 2) C(z 7) 0 .
Искомая плоскость параллельна заданной плоскости. Тогда из условия
параллельности двух плоскостей получим
A 2, B 0, C 3
2 0 3
.
A B C
Отсюда
Подставляя найденные коэффициенты A, B, C в предыдущее уравнение
найдем уравнение искомой плоскости
2(x 3) 3(z 7) 0 2x 3z 27 0.
14. ПРЯМАЯ В ПРОСТРАНСТВЕ . ВЕКТОРНОЕ, КАНОНИЧЕСКИЕ И ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Положениепрямой в пространстве
определяется заданием
любых двух точек;
ее точки и вектора
параллельного этой прямой;
двух пересекающихся
плоскостей
15.
Пустьв
R 3 дана точка M 0 ( x 0 ; y 0 z 0 ) и вектор
пространстве
S m; n; p . Тогда через точку M 0 параллельно вектору S проходит
единственная прямая . Для определения ее уравнения выберем в R 3
произвольную точку M(x; y; z) и построим векторы r0 OM 0 x 0 ; y 0 ; z 0 ,
и r OM x; y; z
z
M0
r0
M
r
S
y
0
х
Рис. 1.24
16.
Согласно определению суммы векторов получим r r0 M 0 MПусть точка M , тогда векторы M 0 M и S коллинеарны. Следовательно, M 0 M t S , где t - параметр, принимающий любое значение
из R в зависимости от положения точки M на прямой . Тогда для точки
M имеем
r r0 t S , где t R
Если точка M , то векторы M 0 M и S не коллинеарны.
Следовательно, для таких точек полученное равенство не выполняется ни
при каких t R. . Итак, полученное уравнение является векторным уравнением прямой. Вектор S m; n; p называется направляющим вектором прямой.
17.
Воспользовавшись координатами векторов r, r0 , S , получимxi y j zk x 0 i y 0 j z 0 k t (mi n j pk )
x x 0 mt ,
y y 0 nt ,
z z pt .
0
Данные уравнения называются параметрическими уравнениями прямой
3
с параметром t в пространстве R .
Исключая параметр t из уравнений найдем, что
x x 0 y y0 z z0
.
m
n
p
Полученные уравнения называются каноническими уравнениями прямой
в пространстве R 3 .
18.
Замечание. В канонических уравнениях прямой условилисьсчитать, что числа m, n и p могут принимать любые значения, кроме
одновременного равенства m, n и p нулю. В частности, если данные
x x 0 y y0 z z0
, то это уравнения
уравнения имеют вид
0
n
m
есть уравнения прямой перпендикулярной оси OZ . Действительно,
при p 0 направляющий вектор S m; n;0 перпендикулярен оси
OZ . Следовательно, и параллельная вектору S прямая перпендикулярна
этой
оси.
Если
же
уравнения
имеют
вид
x x 0 y y0 z z0
,то это уравнение является уравнением
0
n
0
прямой перпендикулярной плоскости XOZ.
19.
ПРИМЕР. Определить, лежит ли точка M1 (8; 7;6) напрямой , проходящей через точку M 0 (2;1; 4) параллельно
вектору S 3; 4;5 .
Решение. Найдем уравнения прямой в канонической
форме. Полагая x 0 2, y 0 1, z 0 4, m 3, n 4, p 5,
получим
x 2 y 1 z 4
:
.
3
4
5
Подставляя в эти уравнения координаты точки M 1 , найдем
8 2 7 1 6 4
2.
3
4
5
Следовательно, точка M 1 принадлежит прямой .
20.
УРАВНЕНИЯ ПРЯМОЙ ПО ДВУМ ЕЕ ТОЧКАМПусть прямая проходит через две данные точки
M1 ( x1 ; y1 ; z1 ), M 2 ( x 2 ; y 2 ; z 2 ).
Вектор M1M 2 x 2 x1 ; y 2 y1 ; z 2 z1 расположен на самой прямой . Следовательно, этот вектор является одним из направляющих векторов S этой прямой. Тогда, полагая, в канонических уравнениях
m x 2 x 1 , n y 2 y1 , p z 2 z 1 , x 0 x 1 , y 0 y1 , z 0 z 1 ,
получим
x x1
y y1
z z1
.
x 2 x1 y 2 y1 z 2 z1
Данные уравнения называются уравнениями прямой по двум
ее точкам
21.
ПРИМЕР. Найти уравнения медианы ( AM ) треугольника свершинами в точках A(1;3; 5), B(0;4; 1), C(6; 2;5)
Решение. Так как точка M делит отрезок BC пополам, то
xb xc 0 6
yb yc 4 2
xm
3, y m
1,
2
2
2
2
zb zc 1 5
zm
2.
2
2
Медиана ( AM ) проходит через точки A и M , координаты
которых известны. Тогда, уравнения этой медианы будут иметь вид
x xa
y ya
z za
x 1 y 3 z 5
x m x a ym ya z m za
3 1 1 3 2 5
x 1 y 3 z 5
.
2
2
7
22.
ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙR3
пространстве
даны
своими
уравнениями
A1 x B1 y C1z D1 0 и A 2 x B2 y C 2 z D 2 0 две плоскости 1 , 2 .
Если эти плоскости пересекаются, то система
Пусть
в
A1 x B1 y C1z D1 0,
A 2 x B 2 y C 2 z D 2 0.
определяет уравнения прямой, являющейся линией пересечения плоскостей 1
и 2 . Данные уравнения называются общими уравнениями прямой.
1
S
N1
2
N2
Рис. 1.25
23.
Покажем, что если прямая задана своими уравнениями в однойиз своих форм, то всегда возможно найти любую из оставшихся ее форм
уравнений. Например, если прямая задана своими каноническими
уравнениями
x x 0 y y0 z z0
, то эти уравнения равносильны системе двух
m
n
p
уравнений первой степени
x x 0 y y0
m n ,
nx my (my 0 nx 0 ) 0,
y y
z
z
0
0
py nz (nz 0 py 0 ) 0.
n
p
Первое уравнение этой системы не содержит z . Следовательно,
оно определяет плоскостью параллельную оси OZ . Второе уравнение
не содержит x и определяет плоскость, параллельную оси OX . Тогда
эта система составлена из уравнений пересекающихся плоскостей и
представляет собой общие уравнения данной прямой .
24.
Пусть, наоборот, прямая дана своими общими уравнениями и требуется найти ее канонические уравнения. Для решения этой задачи достаточноуказать одну из бесконечного множества точек M 0 ( x 0 ; y 0 ; z 0 ) , принадлежащих прямой, и найти направляющий вектор S m; n; p .
Координаты такой точки M 0 проще всего определить из системы
уравнений, если в этой системе положить либо x , либо y , либо z равными
какому угодно числу (например, нулю). Для определения одного из возможных направляющих векторов S прямой построим нормальные векторы
N1 A1 ; B1 ; C1 , N 2 A 2 ; B2 ; C 2 данных плоскостей.
Вектор S перпендикулярен векторам N 1 , N 2 , тогда
i
j
k
S N1 N 2 A1
B1
A2
B2
C1 .
C2
Подставляя найденные координаты точки M 0 и проекции вектора
S
в канонические уравнения найдем искомую каноническую форму уравнений
заданной прямой.
25.
ПРИМЕР. Привести общие уравнения прямойx 2 y 3z 4 0
к каноническому виду.
3
x
2
y
5
z
4
0
Решение. Уравнения прямой ищем в виде x x 0 y y 0 z z 0 .
m
n
p
Для определения координат точки M 0 ( x 0 , y 0 , z 0 ) в общих уравнениях положим, напри-
мер, z 0 . Тогда получим систему из двух уравнений с двумя неизвестными
x и y:
x 2y 4 0
x 2 y 4
y 1
3
x
2
y
4
0
4
x
8
x 2
Итак, точка M 0 (2; 1;0) является одной из точек данной прямой. Для определения одного
из направляющих векторов S m; n; p прямой введем два нормальных вектора N1 1; 2;3 и
N 2 3;2; 5 . Тогда
i
j
S N1 N 2 1 2
3
2
k
3 4i 14 j 8k .
5
Отсюда m 4, n 14, p 8 . Подставляя найденные величины в канонические уравнения,
получим искомую каноническую форму уравнения прямой
x 2 y 1 z
x 2 y 1 z
.
4
14
8
2
7
4
26.
УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИПусть в пространстве R 3 даны две прямые
l1 :
x x 2 y y2 z z2
x x1 y y1 z z1
; l2 :
.
m1
n1
p1
m2
n2
p2
S2
1
1
2
2
S1
Рис. 1.26
Под углом между двумя прямыми в пространстве понимают любой из углов,
образованных двумя прямыми, проведенными из одной точки параллельно данным прямым. Обозначим угол между направляющими векторами
S1 m1 ; n1 ; p1 и S2 m 2 ; n 2 ; p 2 данных прямых через . Тогда один из
смежных углов между прямыми 1 и 2 также равен .
27.
Следовательно,cos
S1 S 2
S1 S 2
m1 m 2 n 1 n 2 p1 p 2
m 1 n 1 p1 m 2 n 2 p 2
2
2
2
2
2
2
.
Заметим, что если 1 2 , то векторы S1 , S2 коллинеарны. Тогда
m1 n1 p1
.
m2 n 2 p2
Данные условия называются условиями параллельности двух
прямых в пространстве R 3 .
Если же 1 2 , то и S1 S2 . Тогда ,
2
cos 0 m1m 2 n1n 2 p1p 2 0 .
Данное условие называется условием перпендикулярности двух
3
прямых в пространстве R .
28.
ПРИМЕР. Найти уравнения прямой, проходящей через точку M 0 (2; 3;4) перпендикулярно двум прямым 1 и 2 .1 :
x 1 y 2 z 3
x 3 y 4 z 2
.
; 2 :
3
4
2
1
5
3
Решение. Так как искомая прямая проходит через данную точку M 0 , то ее уравнения будем искать в виде
x 2 y 3 z 4
, где S m; n; p ее неизвестный направляющий векm
n
p
тор.
По условию искомая прямая перпендикулярна прямым 1 , 2 . Тогда S S1 , S S 2 ,где
S1 3;4; 2 , S 2 1;5;3 есть направляющие векторы данных прямых. Следовательно, за направляющий вектор S можно принять вектор
i
j
k
S S1 S 2 3 4 2 22i 11j 11k.
1 5
3
Тогда m 22, n 11, p 11, а уравнениями искомой прямой являются уравнения
x 2 y 3 z 4
x 2 y 3 z 4
.
22
11
11
2
1
1
29.
ПРЯМАЯ И ПЛОСКОСТЬ3
В ПРОСТРАНСТВЕ R
Угол между прямой и плоскостью
N
S
Рис. 1.27
Под углом между прямой и плоскостью понимают любой из
двух смежных углов, образованных прямой и ее проекцией на
плоскость.
30.
наОбозначим один из смежных углов между прямой и ее проекцией
плоскость через , а угол между нормальным вектором
N A; B; C плоскости и направляющим вектором S m; n; p пря
3
.
мой через . Тогда либо , либо
2
2
Отсюда
или
sin sin cos
2
3
sin sin cos .
2
N S
Следовательно, sin cos
.
N S
Тогда, в координатной форме:
sin
Am Bn Cp
A 2 B2 C 2 m 2 n 2 p 2
.
31.
Частные случаи. Если прямая перпендикулярнаплоскости , то векторы S и N коллинеарны. Тогда
A B C
.
m n p
Если же ,то 0 .
Следовательно и sin 0 .Тогда
Am Bn Cp 0.
Таким образом, нами получены условия перпендикулярности и параллельности прямой и плоскости.
32.
ТОЧКА ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПЛОСКОСТЬЮПусть прямая пересекает плоскость в некоторой точке
M1 ( x1 ; y1 ; z1 ). Тогда для определения координат этой точки достаточно решить систему уравнений
Ax By Cz D 0,
x x
y y0 z z0
0
.
m
n
p
Проще всего решить эту систему переходя от канонической
формы задания уравнения прямой к ее заданию в параметрической
форме, т.е. к форме
x x 0 mt ,
y y 0 nt ,
z z pt ,
0
где t параметр.
33.
Подставляя вместо x, y, z их выражения в первое уравнение системы для определения значения параметра t для точки пересечения,получим
A( x 0 mt ) B( y 0 nt ) C(z 0 pt ) D 0
(Am Bn Cp) t Ax 0 By 0 Cz 0 D .
Так
как
по условию прямая пересекает плоскость, то
Am Bn Cp 0 .Следовательно, значение параметра t для точки пересечения найдется по формуле
Ax 0 By 0 Cz 0 D
t
.
Am Bn Cp
Подставляя найденное значение t в каждое из уравнений для переменных, вычислим координаты x1 , y1 , z1 искомой точки M 1 .
34.
ПРИМЕР. Найти проекцию точки М(9;-13;-18) на плоскость 9x 17 y 15z 23 0 .Решение. Проведем через точку М прямую перпендикулярно заданной плоскости. Уравнения этой прямой будем
искать в форме
x 9 y 13 z 18
.
m
n
p
Из условия перпендикулярности прямой и плоскости при
9 17 15
.
А 19 , B 17, C 15 получим, что
m
n
p
Тогда, за проекции m, n , p направляющего вектора S прямой
можно принять числа m 9, n 17, p 15 .
35.
MN
S
M1
Рис. 1.28
36.
Подставляя их, найдем уравнения перпендикуляра :x 9 y 13 z 18
.
9
17
15
Запишем уравнение прямой в параметрической форме:
x 9 9 t,
y 13 17 t ,
z 18 15 t.
Вычислим значение параметра t для точки пересечения прямой с плоскостью:
Ax 0 By 0 Cz 0 D
9 9 ( 17)( 13) ( 15)( 18) 23
t
1
Am Bn Cp
9 9 ( 17) ( 17) ( 15) ( 15)
Подставляя значение t 1 в уравнения для переменных, найдем
координаты искомой точки
x1 9 9 0, y1 13 17 4, z1 18 15 3.
Ответ: M1 (0;4; 3).
M1 :


































 Математика
Математика








